Дерево решений

Дерево решений — это иерархическая модель поддержки принятия решений , в которой используется древовидная модель решений и их возможных последствий, включая исходы случайных событий, затраты ресурсов и полезность . Это один из способов отображения алгоритма , который содержит только условные операторы управления.

Деревья решений обычно используются в исследовании операций , особенно в анализе решений . ^[1] помогают определить стратегию, которая с наибольшей вероятностью приведет к достижению цели, но также являются популярным инструментом машинного обучения .

Обзор [ править ]

Дерево решений представляет собой структуру, подобную блок-схеме , в которой каждый внутренний узел представляет собой «проверку» атрибута (например, выпадает ли при подбрасывании монеты орел или решка), каждая ветвь представляет результат проверки, а каждый листовой узел представляет собой метка класса (решение, принятое после вычисления всех атрибутов). Пути от корня к листу представляют правила классификации.

При анализе решений дерево решений и тесно связанная с ним диаграмма влияния используются в качестве визуального и аналитического инструмента поддержки принятия решений, где ожидаемые значения (или ожидаемая полезность рассчитываются ) конкурирующих альтернатив.

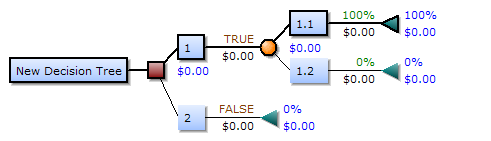
Дерево решений состоит из трех типов узлов: ^[2]

Узлы принятия решений – обычно представляются квадратами.
Случайные узлы – обычно представлены кружками.
Конечные узлы – обычно представляются треугольниками.

Деревья решений обычно используются в исследовании операций и управлении операциями . Если на практике решения необходимо принимать в режиме онлайн без возможности отзыва из-за неполноты знаний, дерево решений должно быть сопоставлено с вероятностной моделью в качестве модели наилучшего выбора или алгоритма модели онлайн-выбора . ^{[ нужна ссылка ]} Другое использование деревьев решений — это описательное средство расчета условных вероятностей .

Деревья решений, диаграммы влияния , функции полезности и другие инструменты и методы анализа решений преподаются студентам бакалавриата в школах бизнеса, экономики здравоохранения и общественного здравоохранения и являются примерами методов исследования операций или науки управления . Эти инструменты также используются для прогнозирования решений домовладельцев в нормальных и чрезвычайных ситуациях. ^[3]^[4]

Строительные блоки дерева решений [ править ]

Элементы дерева решений [ править ]

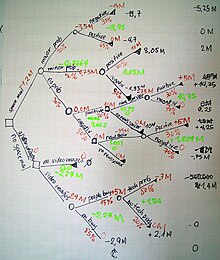
Дерево решений, нарисованное слева направо, имеет только пакетные узлы (разделяющиеся пути), но не имеет приемных узлов (сходящиеся пути). Поэтому, если их использовать вручную, они могут вырасти очень большими, и их часто будет трудно нарисовать полностью вручную. Традиционно деревья решений создавались вручную (как показывает приведенный пример), хотя все чаще используется специализированное программное обеспечение.

Правила принятия решений [ править ]

Дерево решений может быть линеаризовано в правила принятия решений . ^[5] где результатом является содержимое листового узла, а условия на пути образуют конъюнкцию в предложении if. В целом правила имеют вид:

если условие1 , условие2 и условие3, то результат.

Правила принятия решений могут быть созданы путем создания правил ассоциации с целевой переменной справа. Они также могут обозначать временные или причинные отношения. ^[6]

Дерево решений с использованием символов блок-схемы [ править ]

Обычно дерево решений рисуется с использованием символов блок-схемы, поскольку многим его легче читать и понимать. Обратите внимание, что в расчете «Продолжить» дерева, показанного ниже, имеется концептуальная ошибка; ошибка связана с расчетом «издержек», присужденных по судебному иску.

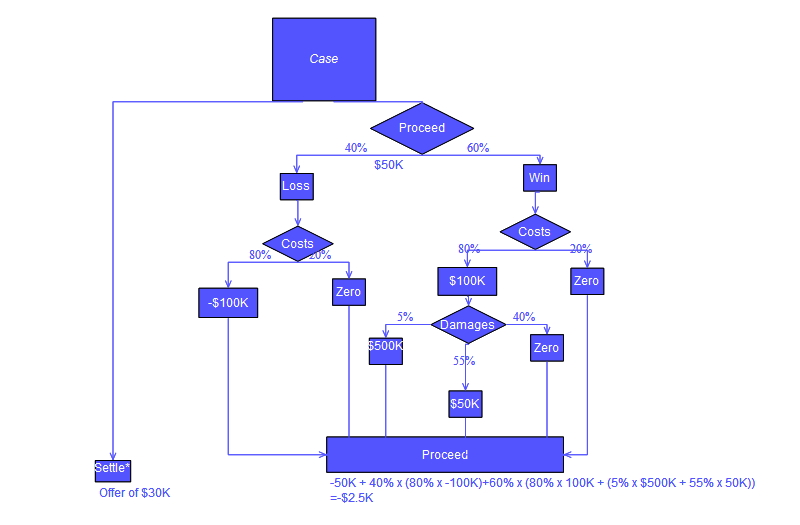
Пример анализа [ править ]

Анализ может учитывать предпочтения лица, принимающего решения (например, компании), или функцию полезности , например:

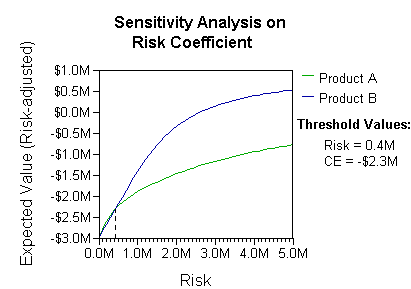
Основная интерпретация этой ситуации заключается в том, что компания предпочитает риск B и выплаты при реалистичных коэффициентах предпочтения риска (более 400 тысяч долларов - в этом диапазоне неприятия риска компании необходимо будет смоделировать третью стратегию: «Ни A, ни B»). .

Другой пример, обычно используемый в курсах по исследованию операций , — это распределение спасателей на пляжах (также известный как пример «Жизнь на пляже»). ^[7] В примере описаны два пляжа со спасателями, которые будут размещены на каждом пляже. Существует максимальный бюджет B , который можно распределить между двумя пляжами (суммарно), и, используя таблицу предельной доходности, аналитики могут решить, сколько спасателей выделить на каждый пляж.


Спасатели на каждом пляже	Всего предотвращено утоплений, пляж №1	Всего предотвращено утоплений, пляж №2
1	3	1
2	0	4

В этом примере можно нарисовать дерево решений, чтобы проиллюстрировать принципы убывающей отдачи на пляже №1.

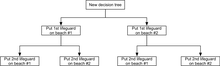
Дерево решений показывает, что при последовательном распределении спасателей размещение первого спасателя на пляже №1 будет оптимальным, если есть бюджет только на 1 спасателя. Но если есть бюджет на двух охранников, то размещение обоих на пляже №2 предотвратит еще больше случаев утопления.

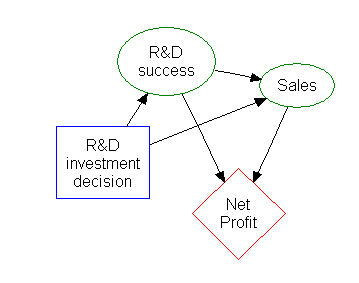
Диаграмма влияния [ править ]

Большую часть информации в дереве решений можно представить более компактно в виде диаграммы влияния , сосредоточив внимание на проблемах и связях между событиями.

Прямоугольник слева представляет решение, овалы — действия, а ромб — результаты.

Индукция правила ассоциации [ править ]

Деревья решений также можно рассматривать как генеративные модели правил индукции на основе эмпирических данных. Оптимальное дерево решений затем определяется как дерево, которое учитывает большую часть данных, при этом минимизируя количество уровней (или «вопросов»). ^[8] Было разработано несколько алгоритмов для создания таких оптимальных деревьев, таких как ID3 /4/5, ^[9] CLS, ПОМОЩНИК и КОРЗИНА.

Преимущества и недостатки [ править ]

Среди инструментов поддержки принятия решений деревья решений (и диаграммы влияния ) имеют ряд преимуществ. Деревья решений:

Просты для понимания и интерпретации. Люди могут понять модели дерева решений после краткого объяснения.
Иметь ценность даже при небольшом количестве точных данных. Важная информация может быть получена на основе описания экспертами ситуации (ее альтернатив, вероятностей и затрат) и их предпочтений в отношении результатов.
Помогите определить худшие, лучшие и ожидаемые значения для различных сценариев.
Используйте модель белого ящика . Если данный результат обеспечивается моделью.
Может сочетаться с другими методами принятия решений.
Можно рассматривать действия более чем одного лица, принимающего решения.

Недостатки деревьев решений:

Они нестабильны, а это означает, что небольшое изменение данных может привести к значительному изменению структуры оптимального дерева решений.
Зачастую они относительно неточны. Многие другие предикторы работают лучше с аналогичными данными. Это можно исправить, заменив одно дерево решений случайным лесом деревьев решений, но случайный лес не так легко интерпретировать, как одно дерево решений.
Для данных, включающих категориальные переменные с разным количеством уровней, прирост информации в деревьях решений смещен в пользу атрибутов с большим количеством уровней. ^[10]
Расчеты могут оказаться очень сложными, особенно если многие значения неопределенны и/или если многие результаты связаны между собой.

Оптимизация дерева решений [ править ]

При повышении точности классификатора дерева решений следует учитывать несколько вещей. Ниже приведены некоторые возможные варианты оптимизации, которые следует учитывать, чтобы убедиться, что созданная модель дерева решений принимает правильное решение или классификацию. Обратите внимание, что это не единственные вещи, которые следует учитывать, а лишь некоторые из них.

Увеличение количества уровней дерева.

Точность дерева решений может меняться в зависимости от глубины дерева решений. Во многих случаях листья дерева представляют собой чистые узлы. ^[11] Когда узел является чистым, это означает, что все данные в этом узле принадлежат одному классу. ^[12] Например, если классами в наборе данных являются рак и нерак, листовой узел будет считаться чистым, если все данные выборки в конечном узле являются частью только одного класса, ракового или неракового. Важно отметить, что более глубокое дерево не всегда лучше при оптимизации дерева решений. Более глубокое дерево может негативно повлиять на время выполнения. Если используется определенный алгоритм классификации, то более глубокое дерево может означать, что время выполнения этого алгоритма классификации значительно медленнее. Существует также вероятность того, что реальный алгоритм построения дерева решений будет работать значительно медленнее по мере того, как дерево становится глубже. Если используемый алгоритм построения дерева разбивает чистые узлы, то может наблюдаться снижение общей точности классификатора дерева. Иногда углубление в дереве может привести к общему снижению точности, поэтому очень важно протестировать изменение глубины дерева решений и выбрать глубину, которая дает наилучшие результаты. Подводя итог, обратите внимание на пункты ниже: мы определим число D как глубину дерева.

Возможные преимущества увеличения числа D:

Повышается точность модели классификации дерева решений.

Возможные недостатки увеличения D

Проблемы во время выполнения
Снижение точности в целом
Чистое разделение узлов при углублении может вызвать проблемы.

Возможность проверки различий в результатах классификации при изменении D является обязательной. Мы должны иметь возможность легко изменять и тестировать переменные, которые могут повлиять на точность и надежность модели дерева решений.

Выбор функций разбиения узлов

Используемая функция разделения узлов может повлиять на повышение точности дерева решений. Например, использование функции получения информации может дать лучшие результаты, чем использование фи-функции. Фи-функция известна как мера «качественности» разделения кандидатов в узле дерева решений. Функция получения информации известна как мера «сокращения энтропии ». Далее мы построим два дерева решений. Одно дерево решений будет построено с использованием функции фи для разделения узлов, а другое дерево решений будет построено с использованием функции получения информации для разделения узлов.

Основные преимущества и недостатки получения информации и фи-функции

Одним из основных недостатков получения информации является то, что признак, выбранный в качестве следующего узла в дереве, имеет тенденцию иметь более уникальные значения. ^[13]
Преимущество сбора информации заключается в том, что он имеет тенденцию выбирать наиболее важные функции, близкие к корню дерева. Это очень хорошая мера для определения актуальности некоторых функций.
Фи-функция также является хорошей мерой для определения релевантности некоторых функций на основе «качественности».

Это формула функции получения информации. Формула утверждает, что прирост информации является функцией энтропии узла дерева решений минус энтропия разделения кандидатов в узле t дерева решений.

$I_{\textrm {gain}}(s)=H(t)-H(s,t)$

Это формула фи-функции. Фи-функция максимизируется, когда выбранный признак разделяет выборки таким образом, чтобы получить однородные разделения и иметь примерно одинаковое количество выборок в каждом разделении.

$\Phi (s,t)=(2*P_{L}*P_{R})*Q(s|t)$

Мы установим D, глубину дерева решений, которое мы строим, равным трем (D = 3). У нас также есть следующий набор данных о раковых и нераковых образцах, а также о функциях мутаций, которые либо есть, либо нет в этих образцах. Если образец имеет мутацию признака, то образец положителен для этой мутации и будет представлен единицей. Если в образце нет мутации признака, то образец отрицателен для этой мутации и будет представлен нулем.

Подводя итог, C означает рак, а NC означает отсутствие рака. Буква M обозначает мутацию , и если образец имеет определенную мутацию, она будет отображаться в таблице как единица, а в противном случае — как ноль.

Пример данных
	М1	М2	M3	М4	М5
С1	0	1	0	1	1
NC1	0	0	0	0	0
NC2	0	0	1	1	0
NC3	0	0	0	0	0
С2	1	1	1	1	1
NC4	0	0	0	1	0

Теперь мы можем использовать формулы для расчета значений фи-функции и значений прироста информации для каждого M в наборе данных. После расчета всех значений можно построить дерево. Первое, что необходимо сделать, это выбрать корневой узел. В области получения информации и фи-функции мы считаем оптимальным разделением ту мутацию, которая дает наибольшее значение прироста информации или фи-функции. Теперь предположим, что M1 имеет самое высокое значение фи-функции, а M4 имеет самое высокое значение прироста информации. Мутация M1 будет корнем нашего фи-функционального дерева, а M4 будет корнем нашего дерева получения информации. Вы можете наблюдать корневые узлы ниже

Figure 1: The left node is the root node of the tree we are building using the phi function to split the nodes. The right node is the root node of the tree we are building using information gain to split the nodes.

Теперь, как только мы выбрали корневой узел, мы можем разделить образцы на две группы в зависимости от того, является ли образец положительным или отрицательным для мутации корневого узла. Группы будут называться группой A и группой B. Например, если мы используем M1 для разделения выборок в корневом узле, мы получим выборки NC2 и C2 в группе A, а остальные выборки NC4, NC3, NC1, C1 в группе. Б.

Не обращая внимания на мутацию, выбранную для корневого узла, приступайте к размещению следующих лучших признаков, которые имеют самые высокие значения для получения информации или функции фи, в левом или правом дочернем узле дерева решений. Как только мы выберем корневой узел и два дочерних узла для дерева глубины = 3, мы можем просто добавить листья. Листья будут представлять собой окончательное решение о классификации, принятое моделью на основе мутаций, которые есть или отсутствуют в образце. Левое дерево — это дерево решений, которое мы получаем в результате использования полученной информации для разделения узлов, а правое дерево — это то, что мы получаем в результате использования функции фи для разделения узлов.

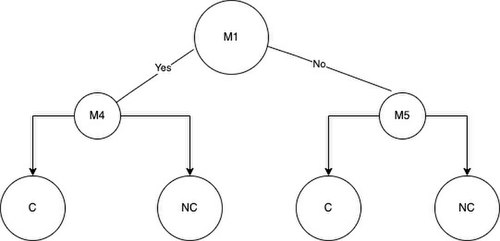
Теперь предположим, что результаты классификации обоих деревьев даны с использованием матрицы путаницы .

Матрица путаницы при получении информации:


	Прогноз: С	Прогноз: Северная Каролина
Фактический: С	1	1
Фактический: Северная Каролина	0	4

Матрица путаницы функций Фи:


	Прогноз: С	Прогноз: Северная Каролина
Фактический: С	2	0
Фактический: Северная Каролина	1	3

Дерево, использующее прирост информации, дает те же результаты при использовании функции фи при расчете точности. Когда мы классифицируем образцы на основе модели с использованием прироста информации, мы получаем один истинно положительный результат, один ложноположительный результат, ноль ложноотрицательных результатов и четыре истинно отрицательных результата. Для модели, использующей функцию фи, мы получаем два истинных положительных результата, ноль ложных положительных результатов, один ложный отрицательный результат и три истинных отрицательных результата. Следующим шагом является оценка эффективности дерева решений с использованием некоторых ключевых показателей, которые будут обсуждаться в разделе «Оценка дерева решений» ниже. Метрики, которые будут обсуждаться ниже, могут помочь определить следующие шаги, которые необходимо предпринять при оптимизации дерева решений.

Другие методы

Приведенная выше информация не ограничивается построением и оптимизацией дерева решений. Существует множество методов улучшения моделей классификации дерева решений, которые мы создаем. Один из методов — создание нашей модели дерева решений из предварительно загруженного набора данных. Загрузочный набор данных помогает устранить предвзятость, возникающую при построении модели дерева решений с теми же данными, на которых тестируется модель. Возможность использовать возможности случайных лесов также может помочь значительно повысить общую точность строящейся модели. Этот метод генерирует множество решений из множества деревьев решений и подсчитывает голоса от каждого дерева решений для окончательной классификации. Существует множество методов, но основная цель — протестировать построение модели дерева решений различными способами, чтобы убедиться, что она достигает максимально возможного уровня производительности.

Оценка дерева решений [ править ]

Важно знать измерения, используемые для оценки деревьев решений. Основными используемыми показателями являются точность , чувствительность , специфичность , прецизионность , уровень ошибок , уровень ложных обнаружений и уровень ложных пропусков . Все эти измерения получены на основе количества истинных положительных результатов , ложных положительных результатов , истинных отрицательных результатов и ложных отрицательных результатов , полученных при прогоне набора образцов через модель классификации дерева решений. Кроме того, для отображения этих результатов можно составить матрицу путаницы. Все эти основные метрики по-разному говорят о сильных и слабых сторонах модели классификации, построенной на основе вашего дерева решений. Например, низкая чувствительность при высокой специфичности может указывать на то, что классификационная модель, построенная на основе дерева решений, не обеспечивает хорошую идентификацию раковых образцов по сравнению с нераковыми образцами.

Давайте возьмем матрицу путаницы ниже. Матрица путаницы показывает, что построенный классификатор модели дерева решений дал 11 истинных положительных результатов, 1 ложный положительный результат, 45 ложных отрицательных результатов и 105 истинных отрицательных результатов.


	Прогноз: С	Прогноз: Северная Каролина
Фактический: С	11	45
Фактический: Северная Каролина	1	105

Теперь мы рассчитаем точность значений, чувствительность, специфичность, точность, частоту ошибок, частоту ложных обнаружений и частоту ложных пропусков.

Точность:

$Accuracy=(TP+TN)/(TP+TN+FP+FN)$

$(11+105)\div 162=71.60\%$

Чувствительность (TPR – истинно положительный уровень): ^[14]

$TPR=TP/(TP+FN)$

$(11)\div (11+45)=19.64\%$

Специфичность (TNR – истинно отрицательный показатель):

$TNR=TN/(TN+FP)$

$105\div (105+1)=99.06\%$

Точность (PPV – положительная прогностическая ценность):

$PPV=TP/(TP+FP)$

$11/(11+1)=91.66\%$

Рейтинг промахов (FNR – ложноотрицательный показатель):

$FNR=FN/(FN+TP)$

$45\div (45+11)=80.35\%$

Уровень ложного обнаружения (FDR):

$FDR=FP/(FP+TP)$

$1\div (1+11)=8.30\%$

Коэффициент ложного пропуска (ЗА):

$FOR=FN/(FN+TN)$

$45\div (45+105)=30.00\%$

После того, как мы рассчитали ключевые показатели, мы можем сделать некоторые первоначальные выводы о производительности построенной модели дерева решений. Точность, которую мы рассчитали, составила 71,60%. Значение точности хорошо для начала, но мы хотели бы, чтобы наши модели были максимально точными, сохраняя при этом общую производительность. Значение чувствительности 19,64% означает, что у всех, у кого действительно был положительный результат на рак, был положительный результат. Если мы посмотрим на значение специфичности 99,06%, мы узнаем, что из всех образцов, которые были отрицательными на рак, тест на самом деле был отрицательным. Когда дело доходит до чувствительности и специфичности, важно иметь баланс между этими двумя значениями, поэтому, если мы сможем уменьшить нашу специфичность, чтобы увеличить чувствительность, это окажется полезным. ^[15] Это всего лишь несколько примеров того, как использовать эти значения и значения, стоящие за ними, для оценки модели дерева решений и улучшения следующей итерации.

См. также [ править ]

Дерево поведения (искусственный интеллект, робототехника и управление) – Математическая модель выполнения плана.
Повышение (машинное обучение) - метод машинного обучения.
Цикл принятия решения - последовательность шагов для принятия решения.
Список решений
Матрица решений
Таблица решений – таблица, определяющая действия в зависимости от условий.
Модель дерева решений - Модель вычислительной сложности вычислений.
Обоснование дизайна – явная документация причин решений, принятых при проектировании системы или артефакта.
DRAKON – Algorithm mapping tool
Цепь Маркова - случайный процесс, не зависящий от прошлой истории.
Случайный лес — метод ансамблевого машинного обучения на основе двоичного дерева поиска.
Подход с порядковым приоритетом - метод анализа решений по множеству критериев.
Алгоритм шансов - метод расчета оптимальных стратегий для задач последнего успеха.
Топологическая комбинаторика
Таблица истинности - математическая таблица, используемая в логике.

Ссылки [ править ]

^ фон Винтерфельдт, Детлоф; Эдвардс, Уорд (1986). «Деревья решений». Анализ решений и поведенческие исследования . Издательство Кембриджского университета. стр. 63–89. ISBN 0-521-27304-8 .
^ Каминский, Б.; Якубчик, М.; Шуфель, П. (2017). «Система анализа чувствительности деревьев решений» . Центральноевропейский журнал исследования операций . 26 (1): 135–159. дои : 10.1007/s10100-017-0479-6 . ПМЦ 5767274 . ПМИД 29375266 .
^ Сюй, Нинчжэ; Ловреглио, Руджеро; Кулиговский, Эрика Д.; Кова, Томас Дж.; Нильссон, Дэниел; Чжао, Силэй (1 марта 2023 г.). «Прогнозирование и оценка принятия решений по эвакуации при лесных пожарах с использованием машинного обучения: результаты пожара в Кинкейде в 2019 году» . Огненная техника . 59 (2): 793–825. дои : 10.1007/s10694-023-01363-1 . ISSN 1572-8099 .
^ Диас-Рамирес, Дженни; Эстрада-Гарсия, Хуан Альберто; Фигероа-Саяго, Хулиана (1 декабря 2023 г.). «Прогнозирование предпочтений в выборе вида транспорта в университетском округе с помощью моделей на основе дерева решений» . Взаимодействие города и окружающей среды . 20 : 100118. doi : 10.1016/j.cacint.2023.100118 . ISSN 2590-2520 .
^ Куинлан, младший (1987). «Упрощение деревьев решений». Международный журнал человеко-машинных исследований . 27 (3): 221–234. CiteSeerX 10.1.1.18.4267 . дои : 10.1016/S0020-7373(87)80053-6 .
^ К. Карими и Х. Дж. Гамильтон (2011), « Генерация и интерпретация временных правил принятия решений », Международный журнал компьютерных информационных систем и приложений промышленного управления, том 3
^ Вагнер, Харви М. (1 сентября 1975 г.). Принципы исследования операций: с применением к управленческим решениям (2-е изд.). Энглвуд Клиффс, Нью-Джерси: Прентис Холл. ISBN 9780137095926 .
^ Р. Куинлан, «Обучение эффективным процедурам классификации» , Машинное обучение: подход искусственного интеллекта , Михальски, Карбонелл и Митчелл (ред.), Морган Кауфманн, 1983, стр. 463–482. дои : 10.1007/978-3-662-12405-5_15
^ Утгофф, ЧП (1989). Поэтапная индукция деревьев решений. Машинное обучение, 4(2), 161–186. два : 10.1023/A:1022699900025
^ Дэн, Х.; Рангер, Г.; Тув, Э. (2011). Смещение показателей важности для многозначных атрибутов и решений . Материалы 21-й Международной конференции по искусственным нейронным сетям (ICANN).
^ Лароз, Шанталь, Даниэль (2014). Обнаружение знаний в данных . Хобокен, Нью-Джерси: John Wiley & Sons. п. 167. ИСБН 9780470908747 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Плапингер, Томас (29 июля 2017 г.). «Что такое дерево решений?» . На пути к науке о данных . Архивировано из оригинала 10 декабря 2021 года . Проверено 5 декабря 2021 г.
^ Тао, Кристофер (6 сентября 2020 г.). «Не используйте дерево решений подобным образом» . На пути к науке о данных . Архивировано из оригинала 10 декабря 2021 года . Проверено 10 декабря 2021 г.
^ «Доля ложноположительных результатов | Разделенный глоссарий» . Расколоть . Проверено 10 декабря 2021 г.
^ «Чувствительность против специфичности» . Анализ и отделение от технологических сетей . Проверено 10 декабря 2021 г.

Внешние ссылки [ править ]

[1] фон Винтерфельдт, Детлоф; Эдвардс, Уорд (1986). «Деревья решений». Анализ решений и поведенческие исследования . Издательство Кембриджского университета. стр. 63–89. ISBN 0-521-27304-8 .

[2] Каминский, Б.; Якубчик, М.; Шуфель, П. (2017). «Система анализа чувствительности деревьев решений» . Центральноевропейский журнал исследования операций . 26 (1): 135–159. дои : 10.1007/s10100-017-0479-6 . ПМЦ 5767274 . ПМИД 29375266 .

[3] Сюй, Нинчжэ; Ловреглио, Руджеро; Кулиговский, Эрика Д.; Кова, Томас Дж.; Нильссон, Дэниел; Чжао, Силэй (1 марта 2023 г.). «Прогнозирование и оценка принятия решений по эвакуации при лесных пожарах с использованием машинного обучения: результаты пожара в Кинкейде в 2019 году» . Огненная техника . 59 (2): 793–825. дои : 10.1007/s10694-023-01363-1 . ISSN 1572-8099 .

[4] Диас-Рамирес, Дженни; Эстрада-Гарсия, Хуан Альберто; Фигероа-Саяго, Хулиана (1 декабря 2023 г.). «Прогнозирование предпочтений в выборе вида транспорта в университетском округе с помощью моделей на основе дерева решений» . Взаимодействие города и окружающей среды . 20 : 100118. doi : 10.1016/j.cacint.2023.100118 . ISSN 2590-2520 .

[5] Куинлан, младший (1987). «Упрощение деревьев решений». Международный журнал человеко-машинных исследований . 27 (3): 221–234. CiteSeerX 10.1.1.18.4267 . дои : 10.1016/S0020-7373(87)80053-6 .

[6] К. Карими и Х. Дж. Гамильтон (2011), « Генерация и интерпретация временных правил принятия решений », Международный журнал компьютерных информационных систем и приложений промышленного управления, том 3

[7] Вагнер, Харви М. (1 сентября 1975 г.). Принципы исследования операций: с применением к управленческим решениям (2-е изд.). Энглвуд Клиффс, Нью-Джерси: Прентис Холл. ISBN 9780137095926 .

[8] Р. Куинлан, «Обучение эффективным процедурам классификации» , Машинное обучение: подход искусственного интеллекта , Михальски, Карбонелл и Митчелл (ред.), Морган Кауфманн, 1983, стр. 463–482. дои : 10.1007/978-3-662-12405-5_15

[9] Утгофф, ЧП (1989). Поэтапная индукция деревьев решений. Машинное обучение, 4(2), 161–186. два : 10.1023/A:1022699900025

[10] Дэн, Х.; Рангер, Г.; Тув, Э. (2011). Смещение показателей важности для многозначных атрибутов и решений . Материалы 21-й Международной конференции по искусственным нейронным сетям (ICANN).

[11] Лароз, Шанталь, Даниэль (2014). Обнаружение знаний в данных . Хобокен, Нью-Джерси: John Wiley & Sons. п. 167. ИСБН 9780470908747 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[12] Плапингер, Томас (29 июля 2017 г.). «Что такое дерево решений?» . На пути к науке о данных . Архивировано из оригинала 10 декабря 2021 года . Проверено 5 декабря 2021 г.

[13] Тао, Кристофер (6 сентября 2020 г.). «Не используйте дерево решений подобным образом» . На пути к науке о данных . Архивировано из оригинала 10 декабря 2021 года . Проверено 10 декабря 2021 г.

[14] «Доля ложноположительных результатов | Разделенный глоссарий» . Расколоть . Проверено 10 декабря 2021 г.

[15] «Чувствительность против специфичности» . Анализ и отделение от технологических сетей . Проверено 10 декабря 2021 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]