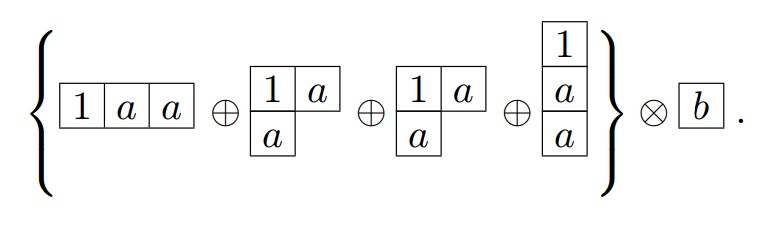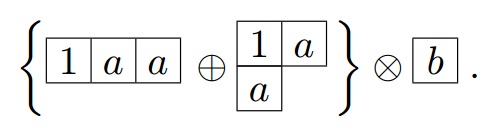Коэффициенты Клебша – Гордана для SU (3)

В математической физике коэффициенты Клебша – Гордана представляют собой коэффициенты разложения полного углового момента собственных состояний в несвязанном базисе тензорных произведений . Математически они определяют разложение тензорного произведения двух неприводимых представлений в прямую сумму неприводимых представлений, где тип и кратность этих неприводимых представлений известны абстрактно. Название происходит от немецких математиков Альфреда Клебша (1833–1872) и Пауля Гордана (1837–1912), которые столкнулись с эквивалентной проблемой в теории инвариантов .

Обобщение коэффициентов Клебша-Гордана на SU(3) полезно из-за их полезности при описании адронных распадов , где существует симметрия аромата SU(3) ( восьмеричный путь ), которая соединяет три легких кварка : верхний , нижний и странный. .

Группа СУ(3)

Основная статья: Особая унитарная группа

Специальная унитарная группа SU — это группа унитарных матриц , определитель которых равен 1. Это множество замкнуто относительно умножения матриц. Все трансформации, характеризующиеся особой унитарной группой, оставляют нормы неизменными. Симметрия SU(3) проявляется в ароматной симметрии легких кварков (среди верхних , нижних и странных кварков), получившей название Восьмеричного пути (физика) . Эта же группа действует в квантовой хромодинамике на цветовые квантовые числа кварков, образующих фундаментальное (триплетное) представление группы.

Группа SU(3) является подгруппой группы U(3) , группы всех унитарных матриц размера 3×3. Условие унитарности накладывает девять ограничений на все 18 степеней свободы комплексной матрицы 3×3. Таким образом, размерность группы U(3) равна 9. Кроме того, умножив U на фазу, e ^iφ оставляет норму неизменной. Таким образом, U(3) можно разложить в прямое произведение U(1)×SU(3)/Z ₃ . Из-за этого дополнительного ограничения SU(3) имеет размерность 8.

Генераторы алгебры Ли

Любую унитарную матрицу U можно записать в виде

$U=e^{iH}\,$

где H — эрмитиан . Элементы SU(3) можно выразить как

$U=e^{i\sum {a_{k}\lambda _{k}}}$

где $\lambda _{k}$ — это 8 линейно независимых матриц, составляющих основу алгебры Ли SU (3) в тройном представлении. Условие определителя единицы требует $\lambda _{k}$ матрицы быть бесследовыми, поскольку

$\det(e^{A})=e^{\operatorname {tr} (A)}$.

Явный базис в фундаментальном 3 представлении может быть построен по аналогии с матричной алгеброй Паули операторов спина. Он состоит из матриц Гелл-Манна ,

${\begin{array}{ccc}\lambda _{1}={\begin{pmatrix}0&1&0\\1&0&0\\0&0&0\end{pmatrix}}&\lambda _{2}={\begin{pmatrix}0&-i&0\\i&0&0\\0&0&0\end{pmatrix}}&\lambda _{3}={\begin{pmatrix}1&0&0\\0&-1&0\\0&0&0\end{pmatrix}}\\\\\lambda _{4}={\begin{pmatrix}0&0&1\\0&0&0\\1&0&0\end{pmatrix}}&\lambda _{5}={\begin{pmatrix}0&0&-i\\0&0&0\\i&0&0\end{pmatrix}}\\\\\lambda _{6}={\begin{pmatrix}0&0&0\\0&0&1\\0&1&0\end{pmatrix}}&\lambda _{7}={\begin{pmatrix}0&0&0\\0&0&-i\\0&i&0\end{pmatrix}}&\lambda _{8}={\frac {1}{\sqrt {3}}}{\begin{pmatrix}1&0&0\\0&1&0\\0&0&-2\end{pmatrix}}.\end{array}}$

Это генераторы группы SU(3) в триплетном представлении, нормированные как

$\operatorname {tr} (\lambda _{j}\lambda _{k})=2\delta _{jk}.$

Структурные константы алгебры Ли группы задаются коммутаторами $\lambda _{k}$

$[\lambda _{j},\lambda _{k}]=2if_{jkl}\lambda _{l}~,$

где $f_{jkl}$ являются ли структурные константы полностью антисимметричными и аналогичны символу Леви-Чивита? $\epsilon _{jkl}$ SU (2) .

В общем случае они исчезают, если не содержат нечетное число индексов из набора {2,5,7}, соответствующих антисимметричному λ s. Примечание $f_{ljk}={\frac {-i}{4}}\mathrm {tr} ([\lambda _{l},\lambda _{j}]\lambda _{k})$.

Более того,

$\{\lambda _{j},\lambda _{k}\}={\frac {4}{3}}\delta _{jk}+2d_{jkl}\lambda _{l}$

где $d_{jkl}$ — полностью симметричные константы коэффициентов. Они исчезают, если число индексов из набора {2,5,7} нечетно. Что касается матриц,

$d_{jkl}={\frac {1}{4}}\operatorname {tr} (\{\lambda _{j},\lambda _{k}\}\lambda _{l})={\frac {1}{4}}\operatorname {tr} (\{\lambda _{k},\lambda _{l}\}\lambda _{j})=d_{klj}=d_{kjl}$

Стандартная основа

Корневая система SU (3) . Шесть корней взаимно наклонены на π /3 , образуя гексагональную решетку: α соответствует изоспину; β к U-спину; и α + β к V-спину.

Несколько иначе нормированный стандартный базис состоит из операторов F-спина , которые определяются как ${\hat {F_{i}}}={\frac {1}{2}}\lambda _{i}$ для 3 и используются для применения к любому представлению этой алгебры .

Базис Картана –Вейля алгебры Ли группы SU(3) получается путем другой замены базиса, где определяется:

${\hat {I}}_{\pm }={\hat {F}}_{1}\pm i{\hat {F}}_{2}$

${\hat {I}}_{3}={\hat {F_{3}}}$

${\hat {V}}_{\pm }={\hat {F}}_{4}\pm i{\hat {F}}_{5}$

${\hat {U}}_{\pm }={\hat {F}}_{6}\pm i{\hat {F}}_{7}$

${\hat {Y}}={\frac {2}{\sqrt {3}}}{\hat {F}}_{8}~.$

Из-за множителей i в этих формулах это технически является основой для комплексификации алгебры Ли su(3), а именно sl(3, C ). Таким образом, предыдущая основа по сути та же, что и в книге Холла.

Алгебра коммутации генераторов

Стандартная форма генераторов группы SU(3) удовлетворяет коммутационным соотношениям , приведенным ниже:

$[{\hat {Y}},{\hat {I}}_{3}]=0,$

$[{\hat {Y}},{\hat {I}}_{\pm }]=0,$

$[{\hat {Y}},{\hat {U}}_{\pm }]=\pm {\hat {U_{\pm }}},$

$[{\hat {Y}},{\hat {V}}_{\pm }]=\pm {\hat {V_{\pm }}},$

$[{\hat {I}}_{3},{\hat {I}}_{\pm }]=\pm {\hat {I_{\pm }}},$

$[{\hat {I}}_{3},{\hat {U}}_{\pm }]=\mp {\frac {1}{2}}{\hat {U_{\pm }}},$

$[{\hat {I}}_{3},{\hat {V}}_{\pm }]=\pm {\frac {1}{2}}{\hat {V_{\pm }}},$

$[{\hat {I}}_{+},{\hat {I}}_{-}]=2{\hat {I}}_{3},$

$[{\hat {U}}_{+},{\hat {U}}_{-}]={\frac {3}{2}}{\hat {Y}}-{\hat {I}}_{3},$

$[{\hat {V}}_{+},{\hat {V}}_{-}]={\frac {3}{2}}{\hat {Y}}+{\hat {I}}_{3},$

$[{\hat {I}}_{+},{\hat {V}}_{-}]=-{\hat {U}}_{-},$

$[{\hat {I}}_{+},{\hat {U}}_{+}]={\hat {V}}_{+},$

$[{\hat {U}}_{+},{\hat {V}}_{-}]={\hat {I}}_{-},$

$[{\hat {I}}_{+},{\hat {V}}_{+}]=0,$

$[{\hat {I}}_{+},{\hat {U}}_{-}]=0,$

$[{\hat {U}}_{+},{\hat {V}}_{+}]=0.$

Все остальные коммутационные соотношения следуют из эрмитова сопряжения этих операторов.

Эти коммутационные соотношения можно использовать для построения неприводимых представлений группы SU(3) .

Представления группы лежат в двумерной I ₃ − Y. плоскости Здесь, ${\hat {I}}_{3}$ обозначает z-компоненту Изоспина и ${\hat {Y}}$ является Гиперзарядом , и они составляют (абелеву) подалгебру Картана полной алгебры Ли. Максимальное число взаимно коммутирующих генераторов алгебры Ли называется ее рангом : SU(3) имеет ранг 2. Остальные 6 генераторов, ± лестничные операторы, соответствуют 6 корням , расположенным на двумерной гексагональной решетке рисунка. .

Операторы Казимира

Основная статья: оператор Казимира

Оператор Казимира — это оператор, коммутирующий со всеми образующими группы Ли. В случае SU (2) квадратичный оператор J ² является единственным независимым таким оператором.

В случае группы SU (3) , напротив, можно построить два независимых оператора Казимира: квадратичный и кубический: это:

${\hat {C_{1}}}=\sum _{k}{\hat {F_{k}}}{\hat {F_{k}}}\qquad \qquad {\hat {C_{2}}}=\sum _{jkl}d_{jkl}{\hat {F_{j}}}{\hat {F_{k}}}{\hat {F_{l}}}~.$

Эти операторы Казимира служат для обозначения неприводимых представлений Ли групповой алгебры SU (3) , поскольку все состояния в данном представлении принимают одно и то же значение для каждого оператора Казимира, который служит тождеством в пространстве с размерностью этого представления. Это связано с тем, что состояния в данном представлении связаны действием генераторов алгебры Ли, а все генераторы коммутируют с операторами Казимира.

Например, для тройного представления D (1,0) собственное значение ⁠ ${\hat {C}}_{1}$⁠ составляет 4/3, а ⁠ ${\hat {C}}_{2}$⁠ , 10/9.

В более общем смысле, из формулы Фрейденталя для общего D ( p,q ) собственное значение из ⁠ ${\hat {C}}_{1}$⁠ есть.

$(p^{2}+q^{2}+3p+3q+pq)/3$.

Собственное значение («коэффициент аномалии») ⁠ ${\hat {C}}_{2}$⁠ это

$(p-q)(3+p+2q)(3+q+2p)/18.$

Это нечетная функция при перестановке p ↔ q . Следовательно, оно обращается в нуль для вещественных представлений p = q , таких как сопряженное D (1,1) , т. е. как ⁠ ${\hat {C}}_{2}$⁠ и аномалии для него исчезают.

Представления группы SU(3)

См. также: Теория представлений полупростых алгебр Ли § Случай sl(3,C)

Неприводимые представления SU(3) анализируются в различных местах, в том числе в книге Холла. Поскольку группа SU(3) односвязна, представления находятся во взаимно однозначном соответствии с представлениями его алгебры Ли. su(3), или комплексификация ее алгебры Ли sl(3, C ).

Мы обозначаем представления как D ( p , q ), где p и q — целые неотрицательные числа, где в физических терминах p — количество кварков, а q — количество антикварков. Математически представление D ( p , q ) может быть построено путем тензорирования вместе p копий стандартного трехмерного представления и q копий двойственного стандартного представления, а затем извлечения неприводимого инвариантного подпространства. (См. также раздел таблиц Юнга ниже: p - количество столбцов с одним ящиком, «кварки», а q - количество столбцов с двойным ящиком, «антикварки»).

Еще один способ представить параметры p и q — это как максимальные собственные значения диагональных матриц.

$H_{1}={\begin{pmatrix}1&0&0\\0&-1&0\\0&0&0\end{pmatrix}},\quad H_{2}={\begin{pmatrix}0&0&0\\0&1&0\\0&0&-1\end{pmatrix}}$.

(Элементы $H_{1}$ и $H_{2}$ представляют собой линейные комбинации элементов ${\hat {I}}_{3}$ и ${\hat {Y}}$, но нормированную так, что собственные значения $H_{1}$ и $H_{2}$ являются целыми числами.) Это следует сравнить с теорией представлений SU(2) , где неприводимые представления помечены максимальным собственным значением одного элемента h .

Представления имеют размерность

Представление 10 ) D (3,0) (барионный декуплет со спином 3/2

$d(p,q)={\frac {1}{2}}(p+1)(q+1)(p+q+2),$

их неприводимые характеры определяются формулами

$\chi ^{p,q}(\theta ,\phi )=e^{i{\frac {\theta }{3}}(2p+q)}\sum \limits _{k=0}^{p}\sum \limits _{l=0}^{q}e^{-i(k+l)\theta }\left({\frac {\sin((k-l+q+1)\phi /2)}{\sin(\phi /2)}}\right),$

и соответствующая мера Хаара есть $\mu (SU(3))=64\sin \left({\frac {\phi }{2}}\right)^{2}\sin \left({\frac {1}{2}}(\theta +\phi /2)\right)^{2}\sin \left({\frac {1}{2}}(\theta -\phi /2)\right)^{2}$ такой, что $-2\pi \leq \phi \leq 2\pi$ и $-3\pi \leq \theta \leq 3\pi$,

$V(SU(3))=\int _{-\pi }^{\pi }\!\int _{-\pi }^{\pi }d\!\left({\frac {\phi }{2}}\right)d\!\left({\frac {\theta }{3}}\right)\mu (SU(3))=\int _{-2\pi }^{2\pi }{\frac {d\phi }{2}}\int _{-3\pi }^{3\pi }{\frac {d\theta }{3}}\mu (SU(3))=24\pi ^{2}.$

Мультиплет SU(3) может быть полностью задан пятью метками, две из которых — собственные значения двух Казимиров — являются общими для всех членов мультиплета. Это обобщает всего лишь две метки мультиплетов SU(2) , а именно собственные значения его квадратичного Казимира и I ₃ .

С $[{\hat {I}}_{3},{\hat {Y}}]=0$, мы можем обозначать различные состояния собственными значениями ${\hat {I}}_{3}$ и ${\hat {Y}}$ операторы, $|t,y\rangle$, для данного собственного значения изоспина Казимира. Действия операторов в этих состояниях таковы:

${\hat {I}}_{3}|t,y\rangle =t|t,y\rangle$

Представление образующих группы SU(3) .

${\hat {Y}}|t,y\rangle =y|t,y\rangle$

${\hat {U}}_{0}|t,y\rangle ={\Bigl (}{\frac {3}{4}}y-{\frac {1}{2}}t{\Bigr )}|t,y\rangle$

${\hat {V}}_{0}|t,y\rangle ={\Bigl (}{\frac {3}{4}}y+{\frac {1}{2}}t{\Bigr )}|t,y\rangle$

${\hat {I}}_{\pm }|t,y\rangle =\alpha |t\pm 1,y\rangle$

${\hat {U}}_{\pm }|t,y\rangle =\beta |t\pm {\frac {1}{2}},y\pm 1\rangle$

${\hat {V}}_{\pm }|t,y\rangle =\gamma |t\mp {\frac {1}{2}},y\pm 1\rangle$

Здесь,

${\hat {U}}_{0}\equiv {\frac {1}{2}}[{\hat {U}}_{+},{\hat {U}}_{-}]={\frac {3}{4}}{\hat {Y}}-{\frac {1}{2}}{\hat {I}}_{3}$

и

${\hat {V}}_{0}\equiv {\frac {1}{2}}[{\hat {V}}_{+},{\hat {V}}_{-}]={\frac {3}{4}}{\hat {Y}}+{\frac {1}{2}}{\hat {I}}_{3}.$

15-мерное представление D (2,1)

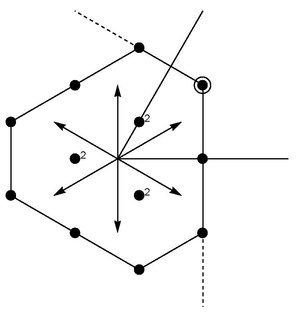
Все остальные состояния представления могут быть построены последовательным применением лестничных операторов. ${\hat {I}}_{\pm },{\hat {U}}_{\pm }$ и ${\hat {V}}_{\pm }$ и путем выявления базовых состояний, которые уничтожаются действием понижающих операторов. Эти операторы можно изобразить в виде стрелок, концы которых образуют вершины шестиугольника (изображение генераторов выше).

См. Также: Модель Кварка

Коэффициент Клебша – Гордана для SU(3)

Представление продукта двух неприводимых представлений $D(p_{1},q_{1})$ и $D(p_{2},q_{2})$ вообще является приводимым. Символически,

$D(p_{1},q_{1})\otimes D(p_{2},q_{2})=\sum _{P,Q}\oplus \sigma (P,Q)D(P,Q)~,$

где ⁠ $\sigma (P,Q)$⁠ — целое число.

Например, два октета (сопряженных) составляют

$D(1,1)\otimes D(1,1)=D(2,2)\oplus D(3,0)\oplus D(1,1)\oplus D(1,1)\oplus D(0,3)\oplus D(0,0)~,$

то есть их произведение сводится к икосасептету ( 27 ), декуплету, двум октетам, антидекуплету и синглету, всего 64 состояния.

Правый ряд называется рядом Клебша–Гордана. Отсюда следует, что представление ⁠ $D(P,Q)$⁠ появляется ⁠ $\sigma (P,Q)$в ⁠ раз в уменьшении этого прямого продукта $D(p_{1},q_{1})$ с $D(p_{2},q_{2})$.

Теперь необходим полный набор операторов, чтобы однозначно определять состояния каждого неприводимого представления внутри только что приведенного. Полный набор коммутирующих операторов в случае неприводимого представления ⁠ $D(P,Q)$⁠ это

$\{{\hat {C}}_{1},{\hat {C}}_{2},{\hat {I}}_{3},{\hat {I}}^{2},{\hat {Y}}\}~,$

где

$I^{2}\equiv {I_{1}}^{2}+{I_{2}}^{2}+{I_{3}}^{2}$.

Таким образом, состояния вышеуказанного прямого представления произведения полностью представляются набором операторов

$\{{\hat {C}}_{1}(1),{\hat {C}}_{2}(1),{\hat {I}}_{3}(1),{\hat {I}}^{2}(1),{\hat {Y}}(1),{\hat {C}}_{1}(2),{\hat {C}}_{2}(2),{\hat {I}}_{3}(2),{\hat {I}}^{2}(2),{\hat {Y}}(2)\},$

где число в скобках обозначает представление, над которым действует оператор.

Альтернативный набор коммутирующих операторов можно найти для прямого представления произведения, если рассмотреть следующий набор операторов:

${\begin{aligned}{\hat {\mathbb {C} }}_{1}&={\hat {C}}_{1}(1)+{\hat {C}}_{1}(2)\\{\hat {\mathbb {C} }}_{2}&={\hat {C}}_{2}(1)+{\hat {C}}_{2}(2)\\{\hat {\mathbb {I} }}^{2}&={\hat {I}}^{2}(1)+{\hat {I}}^{2}(2)\\{\hat {\mathbb {Y} }}&={\hat {Y}}(1)+{\hat {Y}}(2)\\{\hat {\mathbb {I} }}_{3}&={\hat {I}}_{3}(1)+{\hat {I}}_{3}(2).\end{aligned}}$

Таким образом, в набор коммутирующих операторов входит

$\{{\hat {\mathbb {C} }}_{1},{\hat {\mathbb {C} }}_{2},{\hat {\mathbb {Y} }},{\hat {\mathbb {I} }}_{3},{\hat {\mathbb {I} }}^{2},{\hat {C}}_{1}(1),{\hat {C}}_{1}(2),{\hat {C}}_{2}(1),{\hat {C}}_{2}(2)\}.$

Это набор всего из девяти операторов. Но набор должен содержать десять операторов, чтобы однозначно определять все состояния прямого представления произведения. Чтобы найти последний оператор Γ , нужно посмотреть за пределы группы. Необходимо различать разные ⁠ $D(P,Q)$⁠ аналогичных значений P и Q. для

${\begin{array}{cc|cc|cc|cc}{\text{Operator}}&{\text{Eigenvalue}}&{\text{Operator}}&{\text{Eigenvalue}}&{\text{Operator}}&{\text{Eigenvalue}}&{\text{Operator}}&{\text{Eigenvalue}}\\\hline {\hat {C}}_{1}(1)&{c^{1}}_{1}&{\hat {C}}_{1}(2)&{c^{1}}_{2}&{\hat {C}}_{2}(1)&{c^{2}}_{1}&{\hat {C}}_{2}(2)&{c^{2}}_{2}\\{\hat {\mathbb {I} }}^{2}&{i^{2}}&{\hat {\mathbb {I} }}_{3}&{i^{z}}&{\hat {\mathbb {Y} }}&{y}&{\hat {\Gamma }}&\gamma \\{\hat {\mathbb {C} }}_{1}&{c^{1}}&{\hat {\mathbb {C} }}_{2}&{c^{1}}&{\hat {Y}}_{1}&{y}_{1}&{\hat {Y}}_{2}&{y}_{2}\\{\hat {I}}^{2}(1)&{i^{2}}_{1}&{\hat {I}}^{2}(2)&{i^{2}}_{2}&{\hat {I}}_{3}(1)&{i^{z}}_{1}&{\hat {I}}_{3}(2)&{i^{z}}_{2}\end{array}}$

Таким образом, любое состояние в прямом представлении произведения может быть представлено кетом,

$|{c^{1}}_{1},{c^{1}}_{2},{c^{2}}_{1},{c^{2}}_{2},y_{1},y_{2},{i^{2}}_{1},{i^{2}}_{2},{i^{z}}_{1},{i^{z}}_{2}\rangle$

также используя второй полный набор операторов коммутации, мы можем определить состояния в прямом представлении произведения как

$|{c^{1}}_{1},{c^{1}}_{2},{c^{2}}_{1},{c^{2}}_{2},y,\gamma ,{i^{2}},{i^{z}},c^{1},c^{2}\rangle$

Мы можем отказаться от ${c^{1}}_{1},{c^{1}}_{2},{c^{2}}_{1},{c^{2}}_{2}$ от штата и обозначить штаты как

$|y_{1},y_{2},{i^{2}}_{1},{i^{2}}_{2},{i^{z}}_{1},{i^{z}}_{2}\rangle$

используя операторы из первого набора, и,

$|y,\gamma ,{i^{2}},{i^{z}},c^{1},c^{2}\rangle ~,$

используя операторы из второго набора.

Оба этих состояния охватывают прямое представление продукта, и любые состояния в представлении могут быть помечены подходящим выбором собственных значений.

Используя соотношение полноты,

$|y,\gamma ,{i^{2}},{i^{z}},c^{1},c^{2}\rangle =\sum _{y_{1},y_{2}}\sum _{{i^{2}}_{1},{i^{2}}_{2}}\sum _{{i^{z}}_{1},{i^{z}}_{2}}\langle y_{1},y_{2},{i^{2}}_{1},{i^{2}}_{2},{i^{z}}_{1},{i^{z}}_{2}|y,\gamma ,{i^{2}},{i^{z}},c^{1},c^{2}\rangle |y_{1},y_{2},{i^{2}}_{1},{i^{2}}_{2},{i^{z}}_{1},{i^{z}}_{2}\rangle$

Здесь коэффициенты

$\langle y_{1},y_{2},{i^{2}}_{1},{i^{2}}_{2},{i^{z}}_{1},{i^{z}}_{2}|y,\gamma ,{i^{2}},{i^{z}},c^{1},c^{2}\rangle$

– коэффициенты Клебша–Гордана.

Другое обозначение

Во избежание путаницы собственные значения $c^{1},c^{2}$ можно одновременно обозначить через µ и собственные значения $i^{2},i^{z},y$ одновременно обозначаются ν . Тогда собственное состояние представления прямого произведения ⁠ $D(P,Q)$⁠ можно обозначить через

$\psi {\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\&&\nu \end{pmatrix}},$

где $\mu _{1}$ это собственные значения ${c^{1}}_{1},{c^{2}}_{1}$ и $\mu _{2}$ это собственные значения ${c^{1}}_{2},{c^{2}}_{2}$ обозначаются одновременно. Здесь величина, выраженная скобками, представляет собой символ Вигнера 3-j .

Более того, ${\phi ^{\mu _{1}}}_{\nu _{1}}$ считаются базовыми состояниями $D(p_{1},q_{1})$ и ${\phi ^{\mu _{2}}}_{\nu _{2}}$ являются базовыми состояниями $D(p_{2},q_{2})$. Также ${\phi ^{\mu _{1}}}_{\nu _{1}},{\phi ^{\mu _{2}}}_{\nu _{2}}$ являются базовыми состояниями представления продукта. Здесь $\nu _{1},\nu _{2}$ представляет собой объединенные собственные значения $({i^{2}}_{1},{i^{z}}_{1},y_{1})$ и $({i^{2}}_{2},{i^{z}}_{2},y_{2})$ соответственно.

Таким образом, унитарные преобразования, соединяющие два основания, равны

$\psi {\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\&&\nu \end{pmatrix}}=\sum _{\nu _{1},\nu _{2}}{\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}{\phi ^{\mu _{1}}}_{\nu _{1}}{\phi ^{\mu _{2}}}_{\nu _{2}}$

Это сравнительно компактное обозначение. Здесь,

${\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}$

– коэффициенты Клебша–Гордана.

Отношения ортогональности

Коэффициенты Клебша – Гордана образуют действительную ортогональную матрицу. Поэтому,

${\phi ^{\mu _{1}}}_{\nu _{1}}{\phi ^{\mu _{2}}}_{\nu _{2}}=\sum _{\mu ,\nu ,\gamma }{\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}\psi {\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\&&\nu \end{pmatrix}}.$

Кроме того, они следуют следующим соотношениям ортогональности:

$\sum _{\nu _{1},\nu _{2}}{\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}{\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma '\\\nu _{1}&\nu _{2}&\nu '\end{pmatrix}}=\delta _{\nu \nu '}\delta _{\gamma ,\gamma '}$

$\sum _{\mu \nu \gamma }{\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}{\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}'&\nu _{2}'&\nu \end{pmatrix}}=\delta _{\nu _{1}\nu _{1}'}\delta _{\nu _{2},\nu _{2}'}$

Свойства симметрии

Если неприводимое представление ${\scriptstyle {\mu }_{\gamma }}$ появляется в серии Клебша-Гордана. ${\scriptstyle {\mu }_{1}\otimes {\mu }_{2}}$, то он должен появиться в серии Клебша–Гордана ${\scriptstyle {\mu }_{2}\otimes {\mu }_{1}}$. Что подразумевает,

${\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}=\xi _{1}{\begin{pmatrix}\mu _{2}&\mu _{1}&\gamma \\\nu _{2}&\nu _{1}&\nu \end{pmatrix}}$

Где $\xi _{1}=\xi _{1}(\mu _{1},\mu _{2},\gamma )=\pm 1$
Поскольку все коэффициенты Клебша – Гордана действительны, можно вывести следующее свойство симметрии:

${\begin{pmatrix}\mu _{1}&\mu _{2}&\gamma \\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}=\xi _{2}{\begin{pmatrix}{\mu _{1}}^{*}&{\mu _{2}}^{*}&{\gamma }^{*}\\\nu _{1}&\nu _{2}&\nu \end{pmatrix}}$

Где $\xi _{2}=\xi _{2}(\mu _{1},\mu _{2},\gamma )=\pm 1$.

Группа симметрии трехмерного осциллятора гамильтониана оператора

Трехмерный гармонический осциллятор описывается гамильтонианом

${\hat {H}}=-{\tfrac {1}{2}}\nabla ^{2}+{\tfrac {1}{2}}(x^{2}+y^{2}+z^{2}),$

где пружинная константа, масса и постоянная Планка включены в определение переменных, ħ = m =1 .

Видно, что этот гамильтониан симметричен относительно преобразований координат, сохраняющих значение $V=x^{2}+y^{2}+z^{2}$. Таким образом, любые операторы группы SO(3) сохраняют инвариант этого гамильтониана.

Что еще более важно, поскольку гамильтониан является эрмитовым, он, кроме того, остается инвариантным под действием элементов гораздо большей группы SU (3) .

Доказательство того, что группа симметрии линейного изотропного трехмерного гармонического осциллятора равна SU (3).

симметричный (двоичный) тензорный оператор, аналогичный вектору Лапласа–Рунге–Ленца Можно определить для задачи Кеплера:

${\hat {A}}_{ij}={\frac {1}{2}}p_{i}p_{j}+\omega ^{2}r_{i}r_{j}$

который коммутирует с гамильтонианом,

$[{\hat {A}}_{ij},{\hat {H}}]=0.$

Поскольку он коммутирует с гамильтонианом (его следом), он представляет 6−1=5 констант движения.

Он обладает следующими свойствами,

$\sum _{j}{\hat {A}}_{ij}{\hat {L}}_{j}=\sum _{i}{\hat {L}}_{i}{\hat {A}}_{ij}=0$

$\sum _{j}{\hat {A}}_{ij}{\hat {A}}_{jk}={\hat {H}}{\hat {A}}_{ik}+{\frac {1}{4}}\omega ^{2}\{{\hat {L}}_{i}{\hat {L}}_{k}-\delta _{ik}{\hat {L}}^{2}+2[{\hat {L}}_{i},{\hat {L}}_{k}]-2\hbar ^{2}\delta _{ik}\}$

$Tr[{\hat {A}}_{ij}]=\sum _{i}{{\hat {A}}_{ii}}={\hat {H}}.$

Помимо тензорного следа оператора ${\hat {A}}_{ij},$, который является гамильтонианом, оставшиеся 5 операторов можно преобразовать в форму их сферических компонент как

${\hat {A}}_{0}=\omega ^{-1}(2{\hat {A}}_{33}-{\hat {A}}_{11}-{\hat {A}}_{22})$

${\hat {A}}_{\pm }=\mp \omega ^{-1}({\hat {A}}_{13}\pm i{\hat {A}}_{23})$

${\hat {A'}}_{\pm }=\omega ^{-1}({\hat {A}}_{11}-{\hat {A}}_{22}\pm 2i{\hat {A}}_{22})$

Далее операторы углового момента записываются в виде сферических компонент как

${\hat {L}}_{3}={\hat {L}}_{3}$

${\hat {L}}_{\pm }=({\hat {L}}_{1}\pm i{\hat {L}}_{2}).$

Они подчиняются следующим коммутационным соотношениям:

$[{\hat {L}}_{3},{\hat {A}}_{0}]=[{\hat {A}}_{0},{\hat {A'}}_{\pm }]=[{\hat {A}}_{\pm },{\hat {A'}}_{\pm }]=[{\hat {L}}_{\pm },{\hat {A'}}_{\pm }]=0$

$[{\hat {L}}_{\pm },{\hat {L}}_{\mp }]=-4[{\hat {A}}_{\pm },{\hat {A}}_{\mp }]={\frac {1}{2}}[{\hat {A'}}_{\pm },{\hat {A'}}_{\mp }]=\pm 2\hbar {\hat {L}}_{3}$

$[{\hat {L}}_{\pm },{\hat {A}}_{\mp }]=\hbar {\hat {A}}_{0}$

$\pm [{\hat {L}}_{3},{\hat {L}}_{\pm }]=-{\frac {2}{3}}[{\hat {A}}_{0},{\hat {A}}_{\pm }]=[{\hat {A}}_{\mp },{\hat {A'}}_{\pm }]=\hbar {\hat {L}}_{\pm }$

$\pm [{\hat {L}}_{3},{\hat {A}}_{\pm }]=-{\frac {1}{6}}[{\hat {A}}_{0},{\hat {L}}_{\pm }]={\frac {1}{4}}[{\hat {L}}_{\mp },{\hat {A'}}_{\pm }]=\hbar {\hat {A}}_{\pm }$

$\pm [{\hat {L}}_{3},{\hat {A'}}_{\pm }]=2[{\hat {L}}_{\pm },{\hat {A}}_{\pm }]=2\hbar {\hat {A'}}_{\pm }.$

Восемь операторов (состоящих из пяти операторов, полученных из бесследового симметричного тензорного оператора Â _ij и трех независимых компонентов вектора углового момента) подчиняются тем же коммутационным соотношениям, что и бесконечно малые генераторы группы SU (3) , подробно описанные выше.

Таким образом, группа симметрии гамильтониана линейного изотропного трехмерного гармонического осциллятора изоморфна группе SU (3) .

Более систематически такие операторы, как лестничные операторы

${\sqrt {2}}{\hat {a}}_{i}={\hat {X}}_{i}+i{\hat {P}}_{i}~~$ и $~~{\sqrt {2}}{\hat {a}}_{i}^{\dagger }={\hat {X}}_{i}-i{\hat {P}}_{i}$

можно построить, повышающие и понижающие собственное значение оператора Гамильтона на 1.

Операторы â _i и â _i ^† не являются эрмитовыми; но эрмитовы операторы могут быть построены из различных их комбинаций,

а именно, ${\hat {a}}_{i}{\hat {a}}_{j}^{\dagger }$.

для Таких операторов девять i ,j =1,2,3.

Девять эрмитовых операторов, образованных билинейными формами â _i ^† â _j управляются фундаментальными коммутаторами

$[{\hat {a}}_{i},{\hat {a}}_{j}^{\dagger }]=\delta _{ij},$

$[{\hat {a}}_{i},{\hat {a}}_{j}]=[{\hat {a}}_{i}^{\dagger },{\hat {a}}_{j}^{\dagger }]=0,$

и видно, что они не общаются между собой. В результате этот полный набор операторов не имеет общих собственных векторов, и их нельзя диагонализовать одновременно. Таким образом, группа неабелева, и, как указано, в гамильтониане могут присутствовать вырождения.

Гамильтониан трехмерного изотропного гармонического осциллятора, записанный через оператор ${\hat {N_{i}}}={\hat {a}}_{i}^{\dagger }{\hat {a}}_{i}$ составляет

${\hat {H}}=\omega {\bigl [}{\tfrac {3}{2}}+{\hat {N}}_{1}+{\hat {N}}_{2}+{\hat {N}}_{3}{\bigr ]}$.

Гамильтониан имеет 8-кратное вырождение. Последовательное применение â _i и â _j ^† слева сохраняет инвариант гамильтониана, поскольку он увеличивает N _i на 1 и уменьшает N _j на 1, тем самым сохраняя общее количество

$N=\sum {N_{i}}$ постоянный. (ср. квантовый гармонический осциллятор )

См. также: Карта Иордании.

Максимально коммутирующий набор операторов

Поскольку операторы, принадлежащие группе симметрии гамильтониана, не всегда образуют абелеву группу , невозможно найти общий собственный базис, который диагонализует их все одновременно. Вместо этого мы берем максимально коммутирующий набор операторов из группы симметрии гамильтониана и пытаемся свести матричные представления группы к неприводимым представлениям.

См. Также: Полный набор коммутирующих наблюдаемых.

Гильбертово пространство двух систем

Гильбертово пространство двух частиц представляет собой тензорное произведение двух гильбертовых пространств двух отдельных частиц:

$\mathbb {H} =\mathbb {H} _{1}\otimes \mathbb {I} +\mathbb {I} \otimes \mathbb {H} _{2}~,$

где $\mathbb {H} _{1}$ и $\mathbb {H} _{2}$ — гильбертово пространство первой и второй частиц соответственно.

Операторы в каждом из гильбертовых пространств имеют свои коммутационные соотношения, и оператор одного гильбертова пространства коммутирует с оператором из другого гильбертова пространства. Таким образом, группа симметрии двухчастичного оператора Гамильтона является надмножеством групп симметрии гамильтоновых операторов отдельных частиц. Если отдельные гильбертовы пространства N- мерны, объединенное гильбертово пространство N-мерно. ² размерный.

Коэффициент Клебша–Гордана в этом случае

Группа симметрии гамильтониана — SU(3) . В результате коэффициенты Клебша–Гордана можно найти путем разложения несвязанных базисных векторов группы симметрии гамильтониана в его связанный базис. Ряд Клебша – Гордана получается путем блочной диагонализации гамильтониана с помощью унитарного преобразования, построенного на основе собственных состояний, которое диагонализует максимальный набор коммутирующих операторов.

Молодые картины

Основная статья: Молодая картина

Таблица Юнга (множественное число таблиц ) — это метод разложения произведений представления группы SU( N ) в сумму неприводимых представлений. Он обеспечивает размерность и типы симметрии неприводимых представлений, известных как ряд Клебша – Гордана. Каждое неприводимое представление соответствует одночастичному состоянию, а произведение более чем одного неприводимого представления указывает на многочастичное состояние.

Поскольку в квантовой механике частицы по большей части неразличимы, это примерно относится к нескольким перестановочным частицам. Перестановки n частиц составляют симметрическую группу Sn _{одинаковых} . Каждое n -частичное состояние Sn _, состоящее из одночастичных состояний фундаментального N -мерного мультиплета SU(N), принадлежит неприводимому представлению SU(N). Таким образом, его можно использовать для определения ряда Клебша–Гордана для любой унитарной группы.

Построение государств

Любая двухчастичная волновая функция $\psi _{1,2}$, где индексы 1,2 представляют состояние частиц 1 и 2, можно использовать для генерации состояний явной симметрии с помощью симметризирующих и антисимметризирующих операторов.

$\mathbf {S_{12}} =\mathbf {I} +\mathbf {P_{12}}$

$\mathbf {A_{12}} =\mathbf {I} -\mathbf {P_{12}}$

где $\mathbf {P_{12}}$ являются оператором, меняющим местами частицы (оператор обмена).

Отсюда следует следующее соотношение: -

$\mathbf {P_{12}P_{12}} =\mathbf {I}$

$\mathbf {P_{12}S_{12}} =\mathbf {P_{12}} +\mathbf {I} =\mathbf {S_{12}}$

$\mathbf {P_{12}A_{12}} =\mathbf {P_{12}} -\mathbf {I} =-\mathbf {A_{12}}$

$\mathbf {P_{12}} \mathbf {S_{12}} \psi _{12}=+\mathbf {S_{12}} \psi _{12}$

таким образом,

$\mathbf {P_{12}} \mathbf {A_{12}} \psi _{12}=-\mathbf {A_{12}} \psi _{12}.$

Начиная с многочастичного состояния, мы можем применить $\mathbf {S_{12}}$ и $\mathbf {A_{12}}$ неоднократно для создания состояний, которые:

1. Симметричен относительно всех частиц.
2. Антисимметричен относительно всех частиц.
3. Смешанные симметрии, т.е. симметричные или антисимметричные относительно некоторых частиц.

Построение таблиц

Вместо использования ψ в таблицах Юнга мы используем квадратные прямоугольники ( □ ) для обозначения частиц и i для обозначения состояния частиц.

Образец таблицы Янга. Число внутри прямоугольников представляет состояние частиц.

Полный набор $n_{p}$ частицы обозначаются расположением $n_{p}$ □ s, каждый со своей собственной меткой квантового числа ( i ).

Таблицы формируются путем укладки ящиков рядом и вверх-вниз так, что состояния, симметризованные по отношению ко всем частицам, даны подряд, а состояния, антисимметричные по отношению ко всем частицам, лежат в одном столбце. При построении таблиц соблюдаются следующие правила:

1. Ряд не должен быть длиннее предыдущего.
2. Квантовые метки (цифры в □ ) не должны уменьшаться при движении слева направо.
3. Квантовые метки должны строго возрастать при движении вниз по столбцу.

Случай N = 3

При N =3, то есть в случае SU(3), возникает следующая ситуация. В SU(3) есть три метки, они обычно обозначаются (u,d,s), соответствующие верхним, нижним и странным кваркам, которые следуют алгебре SU(3). Их также можно обозначить в общем виде (1,2,3). Для двухчастичной системы мы имеем следующие шесть состояний симметрии:

${{\begin{array}{|c|c|}\hline 1&1\\\hline \end{array}} \atop uu}$

${{\begin{array}{|c|c|}\hline 1&2\\\hline \end{array}} \atop {\frac {1}{\sqrt {2}}}(ud+du)}$

${{\begin{array}{|c|c|}\hline 1&3\\\hline \end{array}} \atop {\frac {1}{\sqrt {2}}}(us+su)}$

${{\begin{array}{|c|c|}\hline 2&2\\\hline \end{array}} \atop dd}$

${{\begin{array}{|c|c|}\hline 2&3\\\hline \end{array}} \atop {\frac {1}{\sqrt {2}}}(ds+sd)}$

${{\begin{array}{|c|c|}\hline 3&3\\\hline \end{array}} \atop ss}$

и следующие три антисимметричных состояния:

${{\begin{array}{|c|}\hline 1\\\hline 2\\\hline \end{array}} \atop {\frac {1}{\sqrt {2}}}(ud-du)}\qquad {{\begin{array}{|c|}\hline 1\\\hline 3\\\hline \end{array}} \atop {\frac {1}{\sqrt {2}}}(us-su)}\qquad {{\begin{array}{|c|}\hline 2\\\hline 3\\\hline \end{array}} \atop {\frac {1}{\sqrt {2}}}(ds-sd)}$

Таблица с 1 столбцом и 3 строками является синглетной, поэтому все таблицы нетривиальных иррепов SU (3) не могут иметь более двух строк. Представление D(p,q) имеет поля p+q в верхнем ряду и поля q во втором ряду.

Серия Клебша – Гордана из картин

Ряд Клебша – Гордана представляет собой разложение тензорного произведения двух неприводимых представлений в прямую сумму неприводимых представлений. $D(p_{1},q_{1})\otimes D(p_{2},q_{2})=\sum _{P,Q}\oplus D(P,Q)$. Это легко выяснить из таблиц Янга.

showПроцедура получения ряда Клебша – Гордана из таблиц Янга:

The following steps are followed to construct the Clebsch–Gordan series from the Young tableaux: Write down the two Young diagrams for the two irreps under consideration, such as in the following example. In the second figure insert a series of the letter a in the first row, the letter b in the second row, the letter c in the third row, etc. in order to keep track of them once they are included in the various resultant diagrams: Take the first box containing an a and appends it to the first Young diagram in all possible ways that follow the rules for creation of a Young diagram: Then take the next box containing an a and do the same thing with it, except that we are not allowed to put two a's together in the same column. The last diagram in the curly bracket contains two a in the same column thus the diagram must be deleted. Thereby giving: Append the last box to the diagram in curly bracket in all possible ways resulting in: In each rows while counting from right to left, if at any point the number of a particular alphabet encountered be more than the number of the previous alphabet, then the diagram must be deleted. Here the first and the third diagram should be deleted, resulting in:

Пример ряда Клебша – Гордана для SU (3)

Тензорное произведение триплета с октетом, сводящимся к деципятиплету ( 15 ), антисекстету и триплету.

$D(1,0)\otimes D(1,1)=D(2,1)\oplus D(0,2)\oplus D(1,0)$

схематически выглядит как -

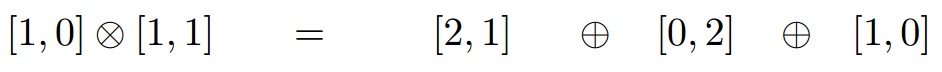
всего 24 штата. Используя ту же процедуру, любое прямое представление продукта легко сокращается.

См. также: Формула длины крючка.

См. также

• D-матрица Вигнера
• Тензорный оператор
• Теорема Вигнера-Экарта
• Теория представлений
• W-коэффициент Рака
• Формула массы Гелл-Манна – Окубо

Ссылки

• Лихтенберг, Д.Б. (2012). Унитарная симметрия и элементарные частицы (2-е изд.). Академическая пресса. ISBN  978-0123941992 .
• Грейнер, В .; Мюллер, Б. (2012). Квантовая механика: Симметрии (2-е изд.). Спрингер. ISBN  978-3540580805 .
• Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для аспирантов по математике, том. 222 (2-е изд.), Спрингер, ISBN  978-3319134666
• МакНэми, П.; ж., С.; Чилтон, Ф. (1964). «Таблицы коэффициентов Клебша-Гордана SU3». Обзоры современной физики . 36 (4): 1005. Бибкод : 1964РвМП...36.1005М . дои : 10.1103/RevModPhys.36.1005 .
• Мандельцвейг, В.Б. (1965). «Неприводимые представления группы SU3». ЖЭТФ СовФиз . 20 (5): 1237–1243. онлайн
• Коулман, Сидни (1965). «Весело с SU(3)» . INSPIREГеп . МАГАТЭ.
• Плухар, З.; Смирнов Ю Ф.; Толстой, В. Н. (1986). «Коэффициенты Клебша-Гордана группы SU (3) с простыми свойствами симметрии». Журнал физики A: Математический и общий . 19 (1): 21–28. Бибкод : 1986JPhA...19...21P . дои : 10.1088/0305-4470/19/1/007 .