Принцип свободной энергии

Принцип свободной энергии — это теоретическая основа, предполагающая, что мозг уменьшает неожиданность или неуверенность, делая прогнозы на основе внутренних моделей и обновляя их с помощью сенсорной информации . Он подчеркивает цель мозга — привести свою внутреннюю модель в соответствие с внешним миром для повышения точности прогнозов . Этот принцип объединяет байесовский вывод с активным выводом , где действия управляются предсказаниями, а сенсорная обратная связь уточняет их. Это имеет широкое значение для понимания функций мозга , восприятия и действий .

Обзор

В биофизике и когнитивной науке принцип свободной энергии — это математический принцип, описывающий формальное описание репрезентативных возможностей физических систем: то есть, почему существующие вещи выглядят так, как будто они отслеживают свойства систем, с которыми они связаны.

Он устанавливает, что динамика физических систем минимизирует величину, известную как неожиданность (которая представляет собой просто отрицательный логарифм вероятности некоторого результата); или, что то же самое, его вариационная верхняя граница, называемая свободной энергией . Этот принцип особенно используется в байесовских подходах к функциям мозга , а также в некоторых подходах к искусственному интеллекту ; формально он связан с вариационными байесовскими методами и первоначально был введен Карлом Фристоном как объяснение воплощенных петель восприятия-действия в нейробиологии .

Принцип свободной энергии моделирует поведение систем, которые отличаются от другой системы, но связаны с ней (например, встроенная среда), где степени свободы, реализующие интерфейс между двумя системами, известны как одеяло Маркова . Более формально, принцип свободной энергии гласит, что если система имеет «определенное разделение» (т. е. на частицы с их марковскими бланкетами), то подмножества этой системы будут отслеживать статистическую структуру других подмножеств (которые известны как внутренние и внешние состояния или пути системы).

Принцип свободной энергии основан на байесовском представлении о мозге как о « машине вывода ». Согласно принципу свободной энергии, системы следуют путями наименьшего неожиданности или, что то же самое, минимизируют разницу между предсказаниями, основанными на их модели мира, и их чувствах и связанном с ними восприятии . Эта разница количественно выражается вариационной свободной энергией и минимизируется путем постоянной коррекции мировой модели системы или путем приведения мира в большее соответствие с предсказаниями системы. Активно изменяя мир, чтобы приблизить его к ожидаемому состоянию, системы также могут минимизировать свободную энергию системы. Фристон полагает, что это принцип всех биологических реакций. Фристон также считает, что его принцип применим как к психическим расстройствам , так и к искусственному интеллекту . Реализации ИИ, основанные на принципе активного вывода, показали преимущества перед другими методами.

Принцип свободной энергии — это математический принцип информационной физики: подобно принципу максимальной энтропии или принципу наименьшего действия, он верен с математической точки зрения. Попытка фальсифицировать принцип свободной энергии является категориальной ошибкой, сродни попытке фальсифицировать исчисление путем проведения эмпирических наблюдений. (Нельзя таким образом опровергнуть математическую теорию; вместо этого нужно было бы вывести из теории формальное противоречие.) В интервью 2018 года Фристон объяснил, что означает, что принцип свободной энергии не подлежит фальсификации : «Я думаю, что на этом этапе полезно провести фундаментальное различие, к которому мы можем обратиться позже. Это различие между теорией состояния и процесса, т. е. различием между нормативным принципом, которому вещи могут соответствовать или не соответствовать, и процессом; теория или гипотеза о том, как этот принцип реализуется. В этом отношении принцип свободной энергии резко отличается от таких вещей, как предсказательное кодирование. и байесовская гипотеза мозга. Это потому, что принцип свободной энергии — это то, что он есть — принцип . Как и принцип стационарного действия Гамильтона , его нельзя фальсифицировать. Это невозможно опровергнуть. Фактически, с этим мало что можно сделать, если только вы не спросите, соответствуют ли измеримые системы этому принципу. С другой стороны, гипотезы о том, что мозг выполняет ту или иную форму байесовского вывода или прогнозирующего кодирования, являются тем, чем они являются — гипотезами. Эти гипотезы могут быть подтверждены или не подтверждены эмпирическими данными». Существует множество примеров того, как эти гипотезы подтверждаются эмпирическими данными.

Предыстория

Представление о том, что самоорганизующиеся биологические системы – такие как клетка или мозг – можно понимать как минимизирующие вариационную свободную энергию, основано на Гельмгольца работе о бессознательном умозаключении. и последующее лечение в психологии и машинное обучение. Вариационная свободная энергия является функцией наблюдений и плотности вероятности их скрытых причин. Эта плотность вариаций определяется в отношении вероятностной модели, которая генерирует прогнозируемые наблюдения на основе гипотетических причин. В этом случае свободная энергия обеспечивает приближение к доказательствам байесовской модели . Следовательно, его минимизацию можно рассматривать как процесс байесовского вывода. Когда система активно проводит наблюдения, чтобы минимизировать свободную энергию, она неявно выполняет активные выводы и максимизирует доказательства своей модели мира.

Однако свободная энергия также является верхней границей самоинформации о результатах, где долгосрочное среднее значение неожиданности — это энтропия. Это означает, что если система стремится минимизировать свободную энергию, она неявно устанавливает верхнюю границу энтропии результатов – или сенсорных состояний – которые она измеряет.

с

Активный вывод тесно связан с теоремой о хорошем регуляторе. и связанные с ним отчеты о самоорганизации , такие как самосборка , формирование узоров , аутопоэзис. и практикопоэз . В нем рассматриваются темы, рассматриваемые в кибернетике , синергетике. и воплощенное познание . Поскольку свободная энергия может быть выражена как ожидаемая энергия наблюдений при вариационной плотности за вычетом ее энтропии, она также связана с принципом максимальной энтропии . Наконец, поскольку усреднение энергии по времени является действием, принцип минимума вариационной свободной энергии является принципом наименьшего действия . Активный вывод, учитывающий масштабную инвариантность, также применялся к другим теориям и областям. Например, это было применено к социологии. лингвистика и коммуникация, семиотика, и эпидемиология среди других.

Отрицательная свободная энергия формально эквивалентна нижней границе доказательства , которая обычно используется в машинном обучении для обучения генеративных моделей , таких как вариационные автоэнкодеры .

и

Рисунок 1: Эти схемы иллюстрируют разделение состояний на внутренние состояния. $\mu (t)$ и внешние (скрытые, латентные) состояния $\psi (t)$ которые разделены марковским одеялом и включают сенсорные состояния. $s(t)$ и активные состояния $a(t)$. Верхняя панель показывает точно такие же зависимости, но перестроенные так, что внутренние состояния связаны с внутриклеточными состояниями клетки, а сенсорные состояния становятся поверхностными состояниями клеточной мембраны, лежащими над активными состояниями (например, актиновыми нитями цитоскелета). . Нижняя панель показывает это разделение применительно к действию и восприятию в мозгу; где активные и внутренние состояния минимизируют функционал свободной энергии сенсорных состояний. Последующая самоорганизация внутренних состояний соответствует восприятию, в то время как действие снова связывает состояния мозга с внешними состояниями.

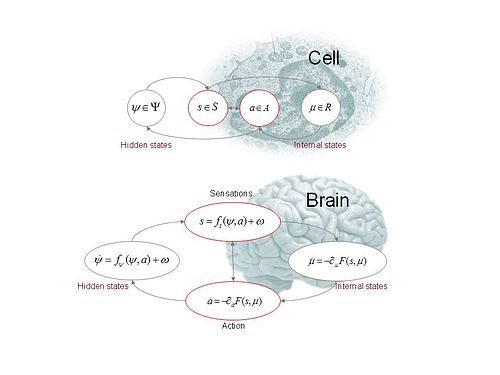
Активный вывод применяет методы приближенного байесовского вывода для вывода причин сенсорных данных из «генеративной» модели того, как эти данные возникают, а затем использует эти выводы для руководства действиями. Правило Байеса характеризует вероятностно оптимальную инверсию такой причинной модели, но ее применение обычно сложно вычислительно, что приводит к использованию приближенных методов.В активном выводе ведущим классом таких приближенных методов являются вариационные методы как по практическим, так и по теоретическим причинам: практические, поскольку они часто приводят к простым процедурам вывода; и теоретические, поскольку они связаны с фундаментальными физическими принципами, как обсуждалось выше.

Эти вариационные методы основаны на минимизации верхней границы расхождения между оптимальным по Байесу выводом (или « апостериорным ») и его аппроксимацией в соответствии с методом.Эта верхняя граница известна как свободная энергия , и мы можем соответственно охарактеризовать восприятие как минимизацию свободной энергии по отношению к входящей сенсорной информации, а действие — как минимизацию той же свободной энергии по отношению к исходящей информации о действии.Эта целостная двойная оптимизация характерна для активного вывода, а принцип свободной энергии представляет собой гипотезу о том, что все системы, которые воспринимают и действуют, могут быть охарактеризованы таким образом.

Чтобы проиллюстрировать механику активного вывода с помощью принципа свободной энергии, необходимо указать генеративную модель, и это обычно включает в себя набор функций плотности вероятности , которые вместе характеризуют причинную модель.Одна из таких спецификаций заключается в следующем.Система моделируется как населяющая пространство состояний. $X$, в том смысле, что его состояния образуют точки этого пространства.Пространство состояний затем факторизуется в соответствии с $X=\Psi \times S\times A\times R$, где $\Psi$ это пространство «внешних» состояний, которые «скрыты» от агента (в том смысле, что они не воспринимаются напрямую или не доступны), $S$ пространство сенсорных состояний, которые непосредственно воспринимаются агентом, $A$ – пространство возможных действий агента, а $R$ представляет собой пространство «внутренних» состояний, которые являются частными для агента.

Следуя рисунку 1, обратите внимание, что в дальнейшем ${\dot {\psi }},\psi ,s,a$ и $\mu$ являются функциями (непрерывного) времени $t$. Генеративная модель представляет собой спецификацию следующих функций плотности:

• Сенсорная модель, $p_{S}:S\times \Psi \times A\to \mathbb {R}$, часто пишется как $p_{S}(s\mid \psi ,a)$, характеризующие вероятность сенсорных данных при заданных внешних состояниях и действиях;
• стохастическая модель динамики окружающей среды, $p_{\Psi }:\Psi \times \Psi \times A\to \mathbb {R}$, часто пишут $p_{\Psi }({\dot {\psi }}\mid \psi ,a)$, характеризующий то, как внешние состояния, по ожиданиям агента, будут развиваться с течением времени $t$, учитывая действия агента;
• модель действия, $p_{A}:A\times R\times S\to \mathbb {R}$, написано $p_{A}(a\mid \mu ,s)$, характеризующий, как действия агента зависят от его внутренних состояний и сенсорных данных; и
• внутренняя модель, $p_{R}:R\times S\to \mathbb {R}$, написано $p_{R}(\mu \mid s)$, характеризующий, как внутренние состояния агента зависят от его сенсорных данных.

Эти функции плотности определяют факторы « совместной модели », которая представляет собой полную спецификацию генеративной модели и которую можно записать как

$p_{\text{Bayes}}({\dot {\psi }},s,a,\mu \mid \psi )=p_{S}(s\mid \psi ,a)p_{\Psi }({\dot {\psi }}\mid \psi ,a)p_{A}(a\mid \mu ,s)p_{R}(\mu \mid s)$.

Затем правило Байеса определяет «апостериорную плотность». $p({\dot {\psi }}|s,a,\mu ,\psi )$, которое выражает вероятностно оптимальное убеждение о внешнем состоянии $\psi$ с учетом предшествующего состояния и действий агента, сенсорных сигналов и внутренних состояний.С момента вычислений $p_{\text{Bayes}}$ является вычислительно неразрешимым, принцип свободной энергии утверждает существование «вариационной плотности». $q({\dot {\psi }}|s,a,\mu ,\psi )$, где $q$ является приближением к $p_{\text{Bayes}}$.Тогда свободную энергию определяют как

${\begin{aligned}{\underset {\mathrm {free-energy} }{\underbrace {F(\mu ,a\,;s)} }}&={\underset {\text{expected energy}}{\underbrace {\mathbb {E} _{q({\dot {\psi }})}[-\log p({\dot {\psi }},s,a,\mu \mid \psi )]} }}-{\underset {\mathrm {entropy} }{\underbrace {\mathbb {H} [q({\dot {\psi }}\mid s,a,\mu ,\psi )]} }}\\&={\underset {\mathrm {surprise} }{\underbrace {-\log p(s)} }}+{\underset {\mathrm {divergence} }{\underbrace {\mathbb {KL} [q({\dot {\psi }}\mid s,a,\mu ,\psi )\parallel p_{\text{Bayes}}({\dot {\psi }}\mid s,a,\mu ,\psi )]} }}\\&\geq {\underset {\mathrm {surprise} }{\underbrace {-\log p(s)} }}\end{aligned}}$

и определяет действие и восприятие как совместную задачу оптимизации.

${\begin{aligned}\mu ^{*}&={\underset {\mu }{\operatorname {arg\,min} }}\{F(\mu ,a\,;\,s))\}\\a^{*}&={\underset {a}{\operatorname {arg\,min} }}\{F(\mu ^{*},a\,;\,s)\}\end{aligned}}$

где внутренние состояния $\mu$ обычно используются для кодирования параметров «вариационной» плотности $q$ и, следовательно, «лучшее предположение» агента об апостериорном убеждении относительно $\Psi$. агента ( предельного или среднего) Обратите внимание, что свободная энергия также является верхней границей меры сенсорного удивления , и, следовательно, минимизация свободной энергии часто мотивируется минимизацией неожиданности.

энергии

самоорганизация

Минимизация свободной энергии была предложена как отличительная черта самоорганизующихся систем, когда они представляют собой случайные динамические системы . Эта формулировка опирается на марковское одеяло (включающее действие и сенсорные состояния), которое разделяет внутренние и внешние состояния. Если внутренние состояния и действия минимизируют свободную энергию, то они устанавливают верхнюю границу энтропии сенсорных состояний:

$\lim _{T\to \infty }{\frac {1}{T}}{\underset {\text{free-action}}{\underbrace {\int _{0}^{T}F(s(t),\mu (t))\,dt} }}\geq \lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}{\underset {\text{surprise}}{\underbrace {-\log p(s(t)\mid m)} }}\,dt=H[p(s\mid m)]$

Это происходит потому, что – согласно эргодическим предположениям – долгосрочное среднее значение неожиданности является энтропией. Эта граница противостоит естественной тенденции к беспорядку, связанной со вторым законом термодинамики и флуктуационной теоремой . Однако формулирование объединяющего принципа для наук о жизни в терминах понятий статистической физики, таких как случайная динамическая система, неравновесное устойчивое состояние и эргодичность, накладывает существенные ограничения на теоретическое и эмпирическое изучение биологических систем с риском затмить все особенности, которые делают биологические системы интересными видами самоорганизующихся систем.

свободной энергии и

Все байесовские выводы можно сделать с точки зрения минимизации свободной энергии. . Когда свободная энергия минимизирована по отношению к внутренним состояниям, расхождение Кульбака – Лейблера между вариационной и апостериорной плотностью по скрытым состояниям минимизируется. Это соответствует приближенному байесовскому выводу – когда форма вариационной плотности фиксирована – и точному байесовскому выводу в противном случае. Таким образом, минимизация свободной энергии обеспечивает общее описание байесовского вывода и фильтрации (например, фильтрации Калмана ). Он также используется при выборе байесовской модели , где свободную энергию можно с пользой разложить на сложность и точность:

${\underset {\text{free-energy}}{\underbrace {F(s,\mu )} }}={\underset {\text{complexity}}{\underbrace {D_{\mathrm {KL} }[q(\psi \mid \mu )\parallel p(\psi \mid m)]} }}-{\underset {\mathrm {accuracy} }{\underbrace {E_{q}[\log p(s\mid \psi ,m)]} }}$

Модели с минимальной свободной энергией обеспечивают точное объяснение данных с учетом издержек сложности (см. бритву Оккама и более формальные подходы к вычислительным затратам). ). Здесь сложность — это расхождение между плотностью вариаций и априорными представлениями о скрытых состояниях (т. е. эффективных степенях свободы, используемых для объяснения данных).

энергии и

Вариационная свободная энергия представляет собой теоретико-информационный функционал и отличается от термодинамической (Гельмгольца) свободной энергии . Однако член сложности вариационной свободной энергии имеет ту же фиксированную точку, что и свободная энергия Гельмгольца (в предположении, что система термодинамически закрыта, но не изолирована). Это связано с тем, что если сенсорные возмущения приостанавливаются (на достаточно длительный период времени), сложность сводится к минимуму (поскольку точностью можно пренебречь). В этот момент система находится в равновесии, а внутренние состояния минимизируют свободную энергию Гельмгольца по принципу минимума энергии .

свободной энергии и

Минимизация свободной энергии эквивалентна максимизации взаимной информации между сенсорными состояниями и внутренними состояниями, которые параметризуют вариационную плотность (для фиксированной вариационной плотности энтропии). Это связывает минимизацию свободной энергии с принципом минимальной избыточности.

свободной энергии

Минимизация свободной энергии обеспечивает полезный способ формулирования нормативных (оптимальных по Байесу) моделей нейронного вывода и обучения в условиях неопределенности. и поэтому поддерживает байесовскую гипотезу мозга . Нейрональные процессы, описываемые минимизацией свободной энергии, зависят от природы скрытых состояний: $\Psi =X\times \Theta \times \Pi$ которые могут включать в себя переменные, зависящие от времени, параметры, не зависящие от времени, и точность (обратную дисперсию или температуру) случайных флуктуаций. Минимизация переменных, параметров и точности соответствует выводу, обучению и кодированию неопределенности соответственно.

и

Минимизация свободной энергии формализует понятие бессознательного вывода в восприятии. и предоставляет нормативную (байесовскую) теорию нейрональной обработки. Соответствующая теория процессов нейронной динамики основана на минимизации свободной энергии посредством градиентного спуска. Это соответствует обобщенной байесовской фильтрации (где ~ обозначает переменную в обобщенных координатах движения, а $D$ является производным матричным оператором):

${\dot {\tilde {\mu }}}=D{\tilde {\mu }}-\partial _{\mu }F(s,\mu ){\Big |}_{\mu ={\tilde {\mu }}}$

Обычно генеративные модели, определяющие свободную энергию, являются нелинейными и иерархическими (например, кортикальные иерархии в мозге). К частным случаям обобщенной фильтрации относится фильтрация Калмана , которая формально эквивалентна предсказательному кодированию. – популярная метафора передачи сообщений в мозгу. В рамках иерархических моделей прогнозирующее кодирование включает в себя периодический обмен ошибками прогнозирования по возрастанию (снизу вверх) и прогнозами по убыванию (сверху вниз). что соответствует анатомии и физиологии сенсорных и двигательные системы.

и

При прогнозирующем кодировании оптимизация параметров модели посредством градиентного спуска по временному интегралу свободной энергии (свободного действия) сводится к ассоциативной или Хеббианской пластичности и связана с синаптической пластичностью в мозге.

, внимание и

Оптимизация параметров точности соответствует оптимизации усиления ошибок прогнозирования (ср. усиление Калмана). В нейронно-правдоподобных реализациях прогнозирующего кодирования это соответствует оптимизации возбудимости поверхностных пирамидных клеток и интерпретируется как усиление внимания.

Моделирование результатов, полученных в результате задачи избирательного внимания, выполненной с помощью байесовской переформулировки SAIM под названием PE-SAIM в среде с множеством объектов. На графиках показано время активации FOA и двух шаблонов в Сети знаний.

Что касается противоречия между принципами «сверху вниз» и «снизу вверх», которое рассматривалось как серьезная открытая проблема, требующая внимания, вычислительная модель сумела проиллюстрировать круговой характер взаимодействия между механизмами «сверху вниз» и «снизу вверх». Используя устоявшуюся эмерджентную модель внимания, а именно SAIM, авторы предложили модель PE-SAIM, которая, в отличие от стандартной версии, рассматривает избирательное внимание с позиции сверху вниз. Модель учитывает передачу ошибок прогнозирования на тот же уровень или уровень выше, чтобы минимизировать энергетическую функцию, указывающую на разницу между данными и их причиной, или, другими словами, между генеративной моделью и апостериорной. . Чтобы повысить достоверность, они также включили в свою модель нейронную конкуренцию между стимулами. Примечательной особенностью этой модели является переформулировка функции свободной энергии только с точки зрения ошибок прогнозирования во время выполнения задачи:

${\dfrac {\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y_{mn}^{SN}}}=x_{mn}^{CN}-b^{CN}\varepsilon _{nm}^{CN}+b^{CN}\sum _{k}(\varepsilon _{knm}^{KN})$

где $E^{total}$ - полная энергетическая функция нейронных сетей, и $\varepsilon _{knm}^{KN}$ — это ошибка прогноза между генеративной моделью (априорной) и апостериорной, изменяющаяся с течением времени. Сравнение двух моделей показывает заметное сходство между их соответствующими результатами, а также подчеркивает заметное несоответствие: в стандартной версии SAIM внимание модели сосредоточено в основном на возбуждающих связях, тогда как в PE-SAIM тормозящие связи использовано для того, чтобы сделать вывод. Модель также доказала свою пригодность для прогнозирования данных ЭЭГ и фМРТ, полученных в ходе экспериментов на людях, с высокой точностью. В том же духе Yahya et al. также применил принцип свободной энергии, чтобы предложить вычислительную модель для сопоставления шаблонов при скрытом избирательном визуальном внимании, которая в основном опирается на SAIM. Согласно этому исследованию, общая свободная энергия всего пространства состояний достигается путем вставки нисходящих сигналов в исходные нейронные сети, в результате чего мы получаем динамическую систему, содержащую как прямую, так и обратную ошибку прогнозирования.

Активный вывод

Когда градиентный спуск применяется к действию ${\dot {a}}=-\partial _{a}F(s,{\tilde {\mu }})$Двигательный контроль можно понимать с точки зрения классических рефлекторных дуг, которые задействуются нисходящими (корково-спинномозговыми) прогнозами. Это обеспечивает формализм, который обобщает решение точки равновесия - на проблему степеней свободы. – траекториям движения.

и

Активный вывод связан с оптимальным управлением путем замены функций ценности или себестоимости предшествующими представлениями о переходах состояний или потоке. При этом используется тесная связь между байесовской фильтрацией и решением уравнения Беллмана . Однако активный вывод начинается с (априорного) потока. $f=\Gamma \cdot \nabla V+\nabla \times W$ которые указаны со скаляром $V(x)$ и вектор $W(x)$ функции ценности пространства состояний (ср. разложение Гельмгольца ). Здесь, $\Gamma$ – амплитуда случайных колебаний, а стоимость – $c(x)=f\cdot \nabla V+\nabla \cdot \Gamma \cdot V$. Приоры над потоком $p({\tilde {x}}\mid m)$ вызвать априорное состояние над состояниями $p(x\mid m)=\exp(V(x))$ это решение соответствующих прямых уравнений Колмогорова . Напротив, оптимальное управление оптимизирует поток с учетом функции стоимости и при условии, что $W=0$ (т. е. поток не имеет завитков или имеет детальный баланс). Обычно это влечет за собой решение обратных уравнений Колмогорова .

решения (игры

оптимального решения Задачи (обычно формулируемые как частично наблюдаемые марковские процессы принятия решений ) рассматриваются в рамках активного вывода путем включения функций полезности в предшествующие убеждения. В этом случае состояния с высокой полезностью (низкой стоимостью) — это состояния, которые агент рассчитывает занять. Оснащая генеративную модель скрытыми состояниями, которые моделируют управление, политики (последовательности управления), которые минимизируют вариационную свободную энергию, приводят к состояниям с высокой полезностью.

С нейробиологической точки зрения считается, что нейромодуляторы, такие как дофамин, сообщают о точности ошибок прогнозирования, модулируя прирост основных клеток, кодирующих ошибку прогнозирования. Это тесно связано с ролью дофамина в сообщении об ошибках прогнозирования как такового , но формально отличается от него. и соответствующие вычислительные счета.

и

Активный вывод использовался для решения ряда проблем когнитивной нейробиологии , функций мозга и нейропсихиатрии, включая наблюдение за действиями, зеркальные нейроны, саккады и зрительный поиск, движения глаз, спать, иллюзии, внимание, выбор действия, сознание, истерия и психоз. Объяснения действий при активном умозаключении часто основаны на идее о том, что у мозга есть «упрямые прогнозы», которые он не может обновить, что приводит к действиям, которые приводят к тому, что эти прогнозы сбываются.

См. также

• Восприятие конкретных действий
• Доступность - Возможность воздействия на объект или окружающую среду.
• Аутопоэзис - концепция системы, предполагающая автоматическое воспроизводство и поддержание.
• Байесовский подход к функционированию мозга – объяснение способностей мозга с помощью статистических принципов
• Конструктивный закон - Закон эволюции дизайна в природе, живой и неживой.
• Теория принятия решений - Раздел прикладной теории вероятностей.
• Воплощенное познание - Междисциплинарная теория
• Энтропийная сила - физическая сила, возникающая из термодинамики, а не из фундаментальных взаимодействий.
• Принцип минимума энергии – термодинамическая формулировка, основанная на втором законе. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Инфо-метрика – Междисциплинарный подход к научному моделированию и обработке информации.
• Оптимальное управление - математический способ достижения желаемого результата от динамической системы.
• Адаптивная система , также известная как практикопоэз – система, способная адаптироваться к окружающей среде.
• Прогнозирующее кодирование - Теория функций мозга
• Самоорганизация - процесс создания порядка посредством местных взаимодействий.
• Сюрприз – базовая величина, полученная на основе вероятности того, что определенное событие произойдет из случайной величины. Страницы, отображающие краткие описания целей перенаправления.
• Синергетика (Хакен) - школа мысли по термодинамике и системным явлениям, разработанная Германом Хакеном. Страницы, отображающие описания из Викиданных в качестве запасного варианта.
• Вариационные байесовские методы . Математические методы, используемые в байесовском выводе и машинном обучении.

Внешние ссылки

• Поведенческие науки и науки о мозге (Энди Кларк)