Гауссова квадратура

«Гауссово интегрирование» перенаправляется сюда. Чтобы узнать об интеграле от функции Гаусса, см. Интеграл Гаусса .

Сравнение двухточечной гауссовой и трапециевидной квадратуры.
Синяя кривая показывает функцию, определенный интеграл которой на интервале [−1, 1] необходимо вычислить (подынтегральная функция). Правило трапеций аппроксимирует функцию линейной функцией, которая совпадает с подынтегральной функцией на концах отрезка и представлена ​​оранжевой пунктирной линией. Аппроксимация, по-видимому, не очень хорошая, поэтому ошибка большая ( правило трапеций дает аппроксимацию интеграла, равную y (–1) + y (1) = –10 , тогда как правильное значение равно 2 ⁄ 3 ). Для получения более точного результата интервал необходимо разбить на множество подинтервалов и затем составное правило трапеций, что требует гораздо большего количества вычислений. использовать
Вместо этого квадратура Гаусса выбирает более подходящие точки, поэтому даже линейная функция лучше аппроксимирует функцию (черная пунктирная линия). Поскольку подынтегральная функция представляет собой многочлен степени 3 ( y ( x ) = 7 x ³ – 8 х ² – 3 x + 3 ), двухточечное квадратурное правило Гаусса даже возвращает точный результат.

В численном анализе используется n - точечное квадратурное правило Гаусса , названное в честь Карла Фридриха Гаусса . — это квадратурное правило, построенное для получения точного результата для многочленов степени 2 n - 1 или меньше путем подходящего выбора узлов x _i и весов w _i для i = 1, ..., n .

Современная формулировка с использованием ортогональных полиномов была разработана Карлом Густавом Якоби в 1826 году. Наиболее распространенной областью интегрирования для такого правила считается [−1, 1] , поэтому правило формулируется как $$\int _{-1}^{1}f(x)\,dx\approx \sum _{i=1}^{n}w_{i}f(x_{i}),$$

что точно для многочленов степени 2 n - 1 или меньше. Это точное правило известно как квадратурное правило Гаусса – Лежандра . Правило квадратур будет точным приближением к приведенному выше интегралу только в том случае, если f ( x ) хорошо аппроксимируется полиномом степени 2 n - 1 или меньше на [−1, 1] .

Квадратурное правило Гаусса – Лежандра обычно не используется для интегрируемых функций с особенностями на концах . Вместо этого, если подынтегральная функция может быть записана как

$$f(x)=\left(1-x\right)^{\alpha }\left(1+x\right)^{\beta }g(x),\quad \alpha ,\beta >-1,$$

где g ( x ) хорошо аппроксимируется полиномом низкой степени, тогда альтернативные узлы x _i ' и веса w _i ' обычно дают более точные правила квадратур. Они известны как квадратурные правила Гаусса – Якоби , т. е.

$$\int _{-1}^{1}f(x)\,dx=\int _{-1}^{1}\left(1-x\right)^{\alpha }\left(1+x\right)^{\beta }g(x)\,dx\approx \sum _{i=1}^{n}w_{i}'g\left(x_{i}'\right).$$

Общие веса включают в себя ${\textstyle {\frac {1}{\sqrt {1-x^{2}}}}}$ ( Чебышев–Гаусс ) и ${\textstyle {\sqrt {1-x^{2}}}}$. Можно также интегрировать по полубесконечным ( квадратура Гаусса-Лагерра ) и бесконечным интервалам ( квадратура Гаусса-Эрмита ).

Можно показать (см. Пресс и др. или Стоер и Булирш), что квадратурные узлы x _i являются корнями многочлена, принадлежащего классу ортогональных многочленов (классу, ортогональному относительно взвешенного скалярного произведения). Это ключевое наблюдение для вычисления квадратурных узлов и весов Гаусса.

Квадратура Гаусса – Лежандра

Дополнительная информация: квадратура Гаусса – Лежандра.

Графики полиномов Лежандра (до n = 5)

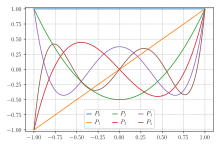
Для простейшей задачи интегрирования, сформулированной выше, т. е. f ( x ) хорошо аппроксимируется полиномами от $[-1,1]$, соответствующие ортогональные полиномы являются полиномами Лежандра , обозначаемыми P _n ( x ) . Когда n -й полином нормализован так, чтобы получить P _n (1) = 1 , i -й узел Гаусса, x _i , является корнем i -й степени из P _n , а веса задаются по формуле $$w_{i}={\frac {2}{\left(1-x_{i}^{2}\right)\left[P'_{n}(x_{i})\right]^{2}}}.$$

Некоторые квадратурные правила низшего порядка приведены в таблице ниже (на интервале [−1, 1] , информацию о других интервалах см. в разделе ниже).

Количество точек, n	Баллы, x i		, Вт Вес
1	0		2
2	$\pm {\frac {1}{\sqrt {3}}}$	±0.57735...	1
3	0		${\frac {8}{9}}$	0.888889...
	$\pm {\sqrt {\frac {3}{5}}}$	±0.774597...	${\frac {5}{9}}$	0.555556...
4	$\pm {\sqrt {{\frac {3}{7}}-{\frac {2}{7}}{\sqrt {\frac {6}{5}}}}}$	±0.339981...	${\frac {18+{\sqrt {30}}}{36}}$	0.652145...
	$\pm {\sqrt {{\frac {3}{7}}+{\frac {2}{7}}{\sqrt {\frac {6}{5}}}}}$	±0.861136...	${\frac {18-{\sqrt {30}}}{36}}$	0.347855...
5	0		${\frac {128}{225}}$	0.568889...
	$\pm {\frac {1}{3}}{\sqrt {5-2{\sqrt {\frac {10}{7}}}}}$	±0.538469...	${\frac {322+13{\sqrt {70}}}{900}}$	0.478629...
	$\pm {\frac {1}{3}}{\sqrt {5+2{\sqrt {\frac {10}{7}}}}}$	±0.90618...	${\frac {322-13{\sqrt {70}}}{900}}$	0.236927...

Изменение интервала

Интеграл по [ a , b ] необходимо заменить на интеграл по [−1, 1] перед применением правила квадратуры Гаусса. Это изменение интервала можно выполнить следующим образом: $$\int _{a}^{b}f(x)\,dx=\int _{-1}^{1}f\left({\frac {b-a}{2}}\xi +{\frac {a+b}{2}}\right)\,{\frac {dx}{d\xi }}d\xi$$

с ${\frac {dx}{d\xi }}={\frac {b-a}{2}}$

Применение $n$ точка Гауссова квадратура $(\xi ,w)$ правило тогда приводит к следующему приближению: $$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{2}}\sum _{i=1}^{n}w_{i}f\left({\frac {b-a}{2}}\xi _{i}+{\frac {a+b}{2}}\right).$$

Пример двухточечного квадратурного правила Гаусса

Используйте правило квадратур Гаусса по двум точкам, чтобы приблизительно определить расстояние в метрах, пройденное ракетой из $t=8\mathrm {s}$ к $t=30\mathrm {s} ,$ как указано $$s=\int _{8}^{30}{\left(2000\ln \left[{\frac {140000}{140000-2100t}}\right]-9.8t\right){dt}}$$

Измените пределы так, чтобы можно было использовать веса и оси абсцисс, приведенные в таблице 1. Также найдите абсолютную относительную истинную ошибку. Истинное значение дано как 11061,34 м.

Решение

Во-первых, изменив пределы интегрирования с $\left[8,30\right]$ к $\left[-1,1\right]$ дает

$${\begin{aligned}\int _{8}^{30}{f(t)dt}&={\frac {30-8}{2}}\int _{-1}^{1}{f\left({\frac {30-8}{2}}x+{\frac {30+8}{2}}\right){dx}}\\&=11\int _{-1}^{1}{f\left(11x+19\right){dx}}\end{aligned}}$$

Затем получите весовые коэффициенты и значения аргументов функции из таблицы 1 для правила двух точек:

• $c_{1}=1.000000000$
• $x_{1}=-0.577350269$
• $c_{2}=1.000000000$
• $x_{2}=0.577350269$

Теперь мы можем использовать квадратурную формулу Гаусса $${\begin{aligned}11\int _{-1}^{1}{f\left(11x+19\right){dx}}&\approx 11\left[c_{1}f\left(11x_{1}+19\right)+c_{2}f\left(11x_{2}+19\right)\right]\\&=11\left[f\left(11(-0.5773503)+19\right)+f\left(11(0.5773503)+19\right)\right]\\&=11\left[f(12.64915)+f(25.35085)\right]\\&=11\left[(296.8317)+(708.4811)\right]\\&=11058.44\end{aligned}}$$с $${\begin{aligned}f(12.64915)&=2000\ln \left[{\frac {140000}{140000-2100(12.64915)}}\right]-9.8(12.64915)\\&=296.8317\end{aligned}}$$$${\begin{aligned}f(25.35085)&=2000\ln \left[{\frac {140000}{140000-2100(25.35085)}}\right]-9.8(25.35085)\\&=708.4811\end{aligned}}$$

Учитывая, что истинное значение составляет 11061,34 м, абсолютная относительная истинная ошибка $\left|\varepsilon _{t}\right|$ является $$\left|\varepsilon _{t}\right|=\left|{\frac {11061.34-11058.44}{11061.34}}\right|\times 100\%=0.0262\%$$

Другие формы

Задачу интегрирования можно выразить несколько более общим способом, введя в подынтегральную функцию положительную весовую функцию ω и допустив интервал, отличный от [−1, 1] . То есть задача состоит в том, чтобы вычислить $$\int _{a}^{b}\omega (x)\,f(x)\,dx$$для некоторых вариантов a , b и ω . Для a = −1 , b = 1 и ω ( x ) = 1 проблема та же, что и рассмотренная выше. Другие варианты ведут к другим правилам интеграции. Некоторые из них представлены в таблице ниже. Номера уравнений указаны для Абрамовица и Стегуна (A и S).

Интервал	ω ( Икс )	Ортогональные полиномы	КАК	Для получения дополнительной информации см....
[−1, 1]	1	Полиномы Лежандра	25.4.29	§ Квадратура Гаусса – Лежандра
(−1, 1)	$\left(1-x\right)^{\alpha }\left(1+x\right)^{\beta },\quad \alpha ,\beta >-1$	Полиномы Якоби	25.4.33 ( β = 0 )	Квадратура Гаусса – Якоби
(−1, 1)	${\frac {1}{\sqrt {1-x^{2}}}}$	Полиномы Чебышева (первого рода)	25.4.38	Квадратура Чебышева – Гаусса
[−1, 1]	${\sqrt {1-x^{2}}}$	Полиномы Чебышева (второго рода)	25.4.40	Квадратура Чебышева – Гаусса
[0, ∞)	$e^{-x}\,$	Полиномы Лагерра	25.4.45	Квадратура Гаусса – Лагерра
[0, ∞)	$x^{\alpha }e^{-x},\quad \alpha >-1$	Обобщенные полиномы Лагерра		Квадратура Гаусса – Лагерра
(−∞, ∞)	$e^{-x^{2}}$	Полиномы Эрмита	25.4.46	Квадратура Гаусса – Эрмита

Основная теорема

Пусть p _n — нетривиальный полином степени n такой, что $$\int _{a}^{b}\omega (x)\,x^{k}p_{n}(x)\,dx=0,\quad {\text{for all }}k=0,1,\ldots ,n-1.$$

Обратите внимание, что это будет верно для всех ортогональных полиномов, приведенных выше, поскольку каждый p _n сконструирован так, чтобы быть ортогональным другим полиномам p _j для j < n и x ^к находится в пределах этого набора.

Если мы выберем n узлов x _i в качестве нулей p _n , то существует n весов w _i , которые делают вычисленный интеграл гауссовой квадратуры точным для всех полиномов h ( x ) степени 2 n - 1 или меньше. Более того, все эти узлы x _i будут лежать в открытом интервале ( a , b ) .

Чтобы доказать первую часть этого утверждения, пусть h ( x ) — любой многочлен степени 2 n − 1 или меньше. Разделите его на ортогональный полином p _n, чтобы получить $$h(x)=p_{n}(x)\,q(x)+r(x).$$где q ( x ) — частное степени n − 1 или меньше (поскольку сумма его степени и степени делителя p _n должна равняться сумме делимого), а r ( x ) — остаток, также степени n − 1 или меньше (поскольку степень остатка всегда меньше степени делителя). Поскольку pn _n меньше по предположению ортогонален всем мономам степени , он должен быть ортогонален фактору q ( x ) . Поэтому $$\int _{a}^{b}\omega (x)\,h(x)\,dx=\int _{a}^{b}\omega (x)\,{\big (}\,p_{n}(x)q(x)+r(x)\,{\big )}\,dx=\int _{a}^{b}\omega (x)\,r(x)\,dx.$$

Поскольку остаток r ( x ) имеет степень n − 1 или меньше, мы можем интерполировать его точно, используя n точек интерполяции с полиномами Лагранжа l _i ( x ) , где $$l_{i}(x)=\prod _{j\neq i}{\frac {x-x_{j}}{x_{i}-x_{j}}}.$$

У нас есть $$r(x)=\sum _{i=1}^{n}l_{i}(x)\,r(x_{i}).$$

Тогда его интеграл будет равен $$\int _{a}^{b}\omega (x)\,r(x)\,dx=\int _{a}^{b}\omega (x)\,\sum _{i=1}^{n}l_{i}(x)\,r(x_{i})\,dx=\sum _{i=1}^{n}\,r(x_{i})\,\int _{a}^{b}\omega (x)\,l_{i}(x)\,dx=\sum _{i=1}^{n}\,r(x_{i})\,w_{i},$$

где w _i , вес, связанный с узлом x _i , определяется как равный взвешенному интегралу от l _i ( x ) (другие формулы для весов см. ниже). Но все x _i являются корнями p _n , поэтому приведенная выше формула деления говорит нам, что $$h(x_{i})=p_{n}(x_{i})\,q(x_{i})+r(x_{i})=r(x_{i}),$$для всех я . Таким образом, мы наконец имеем $$\int _{a}^{b}\omega (x)\,h(x)\,dx=\int _{a}^{b}\omega (x)\,r(x)\,dx=\sum _{i=1}^{n}w_{i}\,r(x_{i})=\sum _{i=1}^{n}w_{i}\,h(x_{i}).$$

Это доказывает, что для любого многочлена h ( x ) степени 2 n - 1 или меньше его интеграл задается в точности квадратурной суммой Гаусса.

Чтобы доказать вторую часть утверждения, рассмотрим факторизованную форму многочлена p _n . Любые комплексно-сопряженные корни дадут квадратичный множитель, который будет либо строго положительным, либо строго отрицательным на всей вещественной прямой. Любые множители для корней вне интервала от a до b не изменят знак на этом интервале. Наконец, для факторов, соответствующих корням x _i внутри интервала от a до b , которые имеют нечетную кратность, умножьте p _n еще на один фактор, чтобы получить новый многочлен $$p_{n}(x)\,\prod _{i}(x-x_{i}).$$

Этот многочлен не может менять знак на интервале от a до b , поскольку все его корни теперь имеют четную кратность. Итак, интеграл $$\int _{a}^{b}p_{n}(x)\,\left(\prod _{i}(x-x_{i})\right)\,\omega (x)\,dx\neq 0,$$поскольку весовая функция ω ( x ) всегда неотрицательна. Но pn _{или меньше, поэтому} ортогонален всем многочленам степени n -1 степень произведения $$\prod _{i}(x-x_{i})$$должно быть не менее n . Следовательно, имеет _pn n различных корней, все действительные, в интервале от a до b .

Общая формула весов

Веса могут быть выражены как

$w_{i}={\frac {a_{n}}{a_{n-1}}}{\frac {\int _{a}^{b}\omega (x)p_{n-1}(x)^{2}dx}{p'_{n}(x_{i})p_{n-1}(x_{i})}}$ ( 1 )

где $a_{k}$ коэффициент $x^{k}$ в $p_{k}(x)$. Чтобы доказать это, заметим, что, используя интерполяцию Лагранжа, можно выразить r ( x ) через $r(x_{i})$ как $$r(x)=\sum _{i=1}^{n}r(x_{i})\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq i\end{smallmatrix}}{\frac {x-x_{j}}{x_{i}-x_{j}}}$$потому что r ( x ) имеет степень меньше n и, таким образом, фиксируется значениями, которые он достигает в n различных точках. Умножая обе части на ω ( x ) и интегрируя от a до b, получаем $$\int _{a}^{b}\omega (x)r(x)dx=\sum _{i=1}^{n}r(x_{i})\int _{a}^{b}\omega (x)\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq i\end{smallmatrix}}{\frac {x-x_{j}}{x_{i}-x_{j}}}dx$$

Таким образом, веса w _i определяются выражением $$w_{i}=\int _{a}^{b}\omega (x)\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq i\end{smallmatrix}}{\frac {x-x_{j}}{x_{i}-x_{j}}}dx$$

Это интегральное выражение для $w_{i}$ можно выразить через ортогональные многочлены $p_{n}(x)$ и $p_{n-1}(x)$ следующее.

Мы можем написать $$\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq i\end{smallmatrix}}\left(x-x_{j}\right)={\frac {\prod _{1\leq j\leq n}\left(x-x_{j}\right)}{x-x_{i}}}={\frac {p_{n}(x)}{a_{n}\left(x-x_{i}\right)}}$$

где $a_{n}$ коэффициент $x^{n}$ в $p_{n}(x)$. Принимая предел x до $x_{i}$ дает по правилу Лопиталя $$\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq i\end{smallmatrix}}\left(x_{i}-x_{j}\right)={\frac {p'_{n}(x_{i})}{a_{n}}}$$

Таким образом, мы можем записать интегральное выражение для весов как

$w_{i}={\frac {1}{p'_{n}(x_{i})}}\int _{a}^{b}\omega (x){\frac {p_{n}(x)}{x-x_{i}}}dx$ ( 2 )

В подынтегральном выражении написав $${\frac {1}{x-x_{i}}}={\frac {1-\left({\frac {x}{x_{i}}}\right)^{k}}{x-x_{i}}}+\left({\frac {x}{x_{i}}}\right)^{k}{\frac {1}{x-x_{i}}}$$

урожайность $$\int _{a}^{b}\omega (x){\frac {x^{k}p_{n}(x)}{x-x_{i}}}dx=x_{i}^{k}\int _{a}^{b}\omega (x){\frac {p_{n}(x)}{x-x_{i}}}dx$$

предоставил $k\leq n$, потому что $${\frac {1-\left({\frac {x}{x_{i}}}\right)^{k}}{x-x_{i}}}$$– многочлен степени k − 1, который тогда ортогонален $p_{n}(x)$. Итак, если q ( x ) является многочленом не более n-й степени, мы имеем $$\int _{a}^{b}\omega (x){\frac {p_{n}(x)}{x-x_{i}}}dx={\frac {1}{q(x_{i})}}\int _{a}^{b}\omega (x){\frac {q(x)p_{n}(x)}{x-x_{i}}}dx$$

Мы можем вычислить интеграл в правой части для $q(x)=p_{n-1}(x)$ следующее. Потому что ${\frac {p_{n}(x)}{x-x_{i}}}$ является многочленом степени n − 1 , имеем $${\frac {p_{n}(x)}{x-x_{i}}}=a_{n}x^{n-1}+s(x)$$где s ( x ) — многочлен степени $n-2$. Поскольку s ( x ) ортогонален $p_{n-1}(x)$ у нас есть $$\int _{a}^{b}\omega (x){\frac {p_{n}(x)}{x-x_{i}}}dx={\frac {a_{n}}{p_{n-1}(x_{i})}}\int _{a}^{b}\omega (x)p_{n-1}(x)x^{n-1}dx$$

Затем мы можем написать $$x^{n-1}=\left(x^{n-1}-{\frac {p_{n-1}(x)}{a_{n-1}}}\right)+{\frac {p_{n-1}(x)}{a_{n-1}}}$$

Член в скобках представляет собой полином степени $n-2$, который поэтому ортогонален $p_{n-1}(x)$. Таким образом, интеграл можно записать как $$\int _{a}^{b}\omega (x){\frac {p_{n}(x)}{x-x_{i}}}dx={\frac {a_{n}}{a_{n-1}p_{n-1}(x_{i})}}\int _{a}^{b}\omega (x)p_{n-1}(x)^{2}dx$$

Согласно уравнению ( 2 ), веса получаются путем деления этого значения на $p'_{n}(x_{i})$ и это дает выражение в уравнении ( 1 ).

$w_{i}$ также может быть выражено через ортогональные многочлены $p_{n}(x)$ и сейчас $p_{n+1}(x)$. В 3-членном рекуррентном соотношении $p_{n+1}(x_{i})=(a)p_{n}(x_{i})+(b)p_{n-1}(x_{i})$ термин с $p_{n}(x_{i})$ исчезает, поэтому $p_{n-1}(x_{i})$ в уравнении (1) можно заменить на ${\textstyle {\frac {1}{b}}p_{n+1}\left(x_{i}\right)}$.

Доказательство того, что веса положительны

Рассмотрим следующий полином степени $2n-2$$$f(x)=\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq i\end{smallmatrix}}{\frac {\left(x-x_{j}\right)^{2}}{\left(x_{i}-x_{j}\right)^{2}}}$$где, как и выше, x _j — корни многочлена $p_{n}(x)$. Четко $f(x_{j})=\delta _{ij}$. Поскольку степень $f(x)$ меньше, чем $2n-1$, квадратурная формула Гаусса, включающая веса и узлы, полученные из $p_{n}(x)$ применяется. С $f(x_{j})=0$ для j, не равного i , мы имеем $$\int _{a}^{b}\omega (x)f(x)dx=\sum _{j=1}^{n}w_{j}f(x_{j})=\sum _{j=1}^{n}\delta _{ij}w_{j}=w_{i}>0.$$

Поскольку оба $\omega (x)$ и $f(x)$ являются неотрицательными функциями, отсюда следует, что $w_{i}>0$.

Вычисление правил квадратур Гаусса

Существует множество алгоритмов вычисления узлов x _i и весов w _i квадратурных правил Гаусса. Наиболее популярными являются алгоритм Голуба-Уэлша, требующий O ( n ² ) операции, метод Ньютона для решения $p_{n}(x)=0$ использование трехчленной повторяемости для оценки, требующей O ( n ² ) операций и асимптотические формулы для больших n, требующих O ( n ) операций.

Рекуррентное отношение

Ортогональные полиномы $p_{r}$ с $(p_{r},p_{s})=0$ для $r\neq s$ для скалярного произведения $(\cdot ,\cdot )$, степень $(p_{r})=r$ и старший коэффициент один (т.е. монические ортогональные полиномы) удовлетворяют рекуррентному соотношению $$p_{r+1}(x)=(x-a_{r,r})p_{r}(x)-a_{r,r-1}p_{r-1}(x)\cdots -a_{r,0}p_{0}(x)$$

и скалярное произведение определено $$(f(x),g(x))=\int _{a}^{b}\omega (x)f(x)g(x)dx$$

для $r=0,1,\ldots ,n-1$ где n — максимальная степень, которую можно принять за бесконечность, и где ${\textstyle a_{r,s}={\frac {\left(xp_{r},p_{s}\right)}{\left(p_{s},p_{s}\right)}}}$. Прежде всего, полиномы, определяемые рекуррентным соотношением, начиная с $p_{0}(x)=1$ имеют ведущий коэффициент один и правильную степень. Учитывая отправную точку $p_{0}$, ортогональность $p_{r}$ можно показать по индукции. Для $r=s=0$ у одного есть $$(p_{1},p_{0})=(x-a_{0,0})(p_{0},p_{0})=(xp_{0},p_{0})-a_{0,0}(p_{0},p_{0})=(xp_{0},p_{0})-(xp_{0},p_{0})=0.$$

Теперь, если $p_{0},p_{1},\ldots ,p_{r}$ ортогональны, то также $p_{r+1}$, потому что в $$(p_{r+1},p_{s})=(xp_{r},p_{s})-a_{r,r}(p_{r},p_{s})-a_{r,r-1}(p_{r-1},p_{s})\cdots -a_{r,0}(p_{0},p_{s})$$все скалярные произведения исчезают, кроме первого и того, где $p_{s}$ соответствует тому же ортогональному многочлену. Поэтому, $$(p_{r+1},p_{s})=(xp_{r},p_{s})-a_{r,s}(p_{s},p_{s})=(xp_{r},p_{s})-(xp_{r},p_{s})=0.$$

Однако если скалярное произведение удовлетворяет $(xf,g)=(f,xg)$ (что имеет место в квадратуре Гаусса), рекуррентное соотношение сводится к трехчленному рекуррентному соотношению: $s<r-1,xp_{s}$ является многочленом степени меньше или равной r − 1 . С другой стороны, $p_{r}$ ортогонален каждому многочлену степени меньше или равной r − 1 . Следовательно, у человека есть $(xp_{r},p_{s})=(p_{r},xp_{s})=0$ и $a_{r,s}=0$ для s < р - 1 . Тогда рекуррентное соотношение упрощается до $$p_{r+1}(x)=(x-a_{r,r})p_{r}(x)-a_{r,r-1}p_{r-1}(x)$$

или $$p_{r+1}(x)=(x-a_{r})p_{r}(x)-b_{r}p_{r-1}(x)$$

(с соглашением $p_{-1}(x)\equiv 0$) где $$a_{r}:={\frac {(xp_{r},p_{r})}{(p_{r},p_{r})}},\qquad b_{r}:={\frac {(xp_{r},p_{r-1})}{(p_{r-1},p_{r-1})}}={\frac {(p_{r},p_{r})}{(p_{r-1},p_{r-1})}}$$

(последнее из-за $(xp_{r},p_{r-1})=(p_{r},xp_{r-1})=(p_{r},p_{r})$, с $xp_{r-1}$ отличается от $p_{r}$ на степень меньше r ).

Алгоритм Голуба-Уэлша

Трехчленное рекуррентное соотношение можно записать в матричной форме $J{\tilde {P}}=x{\tilde {P}}-p_{n}(x)\mathbf {e} _{n}$ где ${\tilde {P}}={\begin{bmatrix}p_{0}(x)&p_{1}(x)&\cdots &p_{n-1}(x)\end{bmatrix}}^{\mathsf {T}}$, $\mathbf {e} _{n}$ это $n$стандартный базисный вектор, т.е. $\mathbf {e} _{n}={\begin{bmatrix}0&\cdots &0&1\end{bmatrix}}^{\mathsf {T}}$, а J — следующая трехдиагональная матрица , называемая матрицей Якоби: $$\mathbf {J} ={\begin{bmatrix}a_{0}&1&0&\cdots &0\\b_{1}&a_{1}&1&\ddots &\vdots \\0&b_{2}&\ddots &\ddots &0\\\vdots &\ddots &\ddots &a_{n-2}&1\\0&\cdots &0&b_{n-1}&a_{n-1}\end{bmatrix}}.$$

Нули $x_{j}$ полиномов до степени n , которые используются в качестве узлов квадратуры Гаусса, можно найти путем вычисления собственных значений этой матрицы. Эта процедура известна как алгоритм Голуба – Уэлша .

Для вычисления весов и узлов предпочтительно рассматривать симметричную трехдиагональную матрицу ${\mathcal {J}}$ с элементами $${\begin{aligned}{\mathcal {J}}_{k,i}=J_{k,i}&=a_{k-1}&k&=1,2,\ldots ,n\\[2.1ex]{\mathcal {J}}_{k-1,i}={\mathcal {J}}_{k,k-1}={\sqrt {J_{k,k-1}J_{k-1,k}}}&={\sqrt {b_{k-1}}}&k&={\hphantom {1,\,}}2,\ldots ,n.\end{aligned}}$$

То есть,

$${\mathcal {J}}={\begin{bmatrix}a_{0}&{\sqrt {b_{1}}}&0&\cdots &0\\{\sqrt {b_{1}}}&a_{1}&{\sqrt {b_{2}}}&\ddots &\vdots \\0&{\sqrt {b_{2}}}&\ddots &\ddots &0\\\vdots &\ddots &\ddots &a_{n-2}&{\sqrt {b_{n-1}}}\\0&\cdots &0&{\sqrt {b_{n-1}}}&a_{n-1}\end{bmatrix}}.$$

Джей и ${\mathcal {J}}$ являются похожими матрицами и, следовательно, имеют одинаковые собственные значения (узлы). Веса можно вычислить по соответствующим собственным векторам: Если $\phi ^{(j)}$ является нормализованным собственным вектором (т. е. собственным вектором с евклидовой нормой, равной единице), связанным с собственным значением x _j , соответствующий вес может быть вычислен из первого компонента этого собственного вектора, а именно: $$w_{j}=\mu _{0}\left(\phi _{1}^{(j)}\right)^{2}$$

где $\mu _{0}$ является интегралом весовой функции $$\mu _{0}=\int _{a}^{b}\omega (x)dx.$$

См., например, ( Gil, Segura & Temme 2007 более подробную информацию ).

Оценки ошибок

Погрешность квадратурного правила Гаусса можно сформулировать следующим образом. Для подынтегральной функции, имеющей 2 n непрерывных производных, $$\int _{a}^{b}\omega (x)\,f(x)\,dx-\sum _{i=1}^{n}w_{i}\,f(x_{i})={\frac {f^{(2n)}(\xi )}{(2n)!}}\,(p_{n},p_{n})$$для некоторого ξ в ( a , b ) , где pn _— унитарный (т.е. старший коэффициент равен 1 ) ортогональный полином степени n и где $$(f,g)=\int _{a}^{b}\omega (x)f(x)g(x)\,dx.$$

В важном частном случае ω ( x ) = 1 мы имеем оценку погрешности $${\frac {\left(b-a\right)^{2n+1}\left(n!\right)^{4}}{(2n+1)\left[\left(2n\right)!\right]^{3}}}f^{(2n)}(\xi ),\qquad a<\xi <b.$$

Стоер и Булирш отмечают, что эта оценка ошибки неудобна на практике, поскольку может быть трудно оценить производную порядка 2 n , и, кроме того, фактическая ошибка может быть намного меньше границы, установленной производной. Другой подход заключается в использовании двух правил квадратур Гаусса разного порядка и оценке ошибки как разницы между двумя результатами. Для этой цели могут быть полезны квадратурные правила Гаусса – Кронрода.

Правила Гаусса – Кронрода

Основная статья: квадратурная формула Гаусса – Кронрода

Если интервал [ a , b ] подразделяется, точки оценки Гаусса новых подинтервалов никогда не совпадают с предыдущими точками оценки (за исключением нуля для нечетных чисел), и поэтому подынтегральная функция должна вычисляться в каждой точке. Правила Гаусса – Кронрода представляют собой расширения квадратурных правил Гаусса, созданные путем добавления n + 1 точки к правилу из n точек таким образом, что полученное правило имеет порядок 2 n + 1 . Это позволяет вычислять оценки более высокого порядка, повторно используя значения функции оценки более низкого порядка. Разницу между правилом квадратур Гаусса и его расширением Кронрода часто используют для оценки ошибки аппроксимации.

Правила Гаусса – Лобатто

Также известна как квадратура Лобатто . назван в честь голландского математика Рехуэля Лобатто . Он похож на квадратуру Гаусса со следующими отличиями:

1. Точки интегрирования включают конечные точки интервала интегрирования.
2. Это верно для полиномов до степени 2 n – 3 , где n — количество точек интегрирования.

Квадратура Лобатто функции f ( x ) на интервале [−1, 1] : $$\int _{-1}^{1}{f(x)\,dx}={\frac {2}{n(n-1)}}[f(1)+f(-1)]+\sum _{i=2}^{n-1}{w_{i}f(x_{i})}+R_{n}.$$

Абсцисса: x _i — это $(i-1)$нулевой уровень $P'_{n-1}(x)$, здесь $P_{m}(x)$ обозначает стандартный полином Лежандра m -й степени, а черточка обозначает производную.

Вес: $$w_{i}={\frac {2}{n(n-1)\left[P_{n-1}\left(x_{i}\right)\right]^{2}}},\qquad x_{i}\neq \pm 1.$$

Остаток: $$R_{n}={\frac {-n\left(n-1\right)^{3}2^{2n-1}\left[\left(n-2\right)!\right]^{4}}{(2n-1)\left[\left(2n-2\right)!\right]^{3}}}f^{(2n-2)}(\xi ),\qquad -1<\xi <1.$$

Некоторые из весов:

Количество точек, n	Баллы, x i	, Вт Вес
$3$	$0$	${\frac {4}{3}}$
	$\pm 1$	${\frac {1}{3}}$
$4$	$\pm {\sqrt {\frac {1}{5}}}$	${\frac {5}{6}}$
	$\pm 1$	${\frac {1}{6}}$
$5$	$0$	${\frac {32}{45}}$
	$\pm {\sqrt {\frac {3}{7}}}$	${\frac {49}{90}}$
	$\pm 1$	${\frac {1}{10}}$
$6$	$\pm {\sqrt {{\frac {1}{3}}-{\frac {2{\sqrt {7}}}{21}}}}$	${\frac {14+{\sqrt {7}}}{30}}$
	$\pm {\sqrt {{\frac {1}{3}}+{\frac {2{\sqrt {7}}}{21}}}}$	${\frac {14-{\sqrt {7}}}{30}}$
	$\pm 1$	${\frac {1}{15}}$
$7$	$0$	${\frac {256}{525}}$
	$\pm {\sqrt {{\frac {5}{11}}-{\frac {2}{11}}{\sqrt {\frac {5}{3}}}}}$	${\frac {124+7{\sqrt {15}}}{350}}$
	$\pm {\sqrt {{\frac {5}{11}}+{\frac {2}{11}}{\sqrt {\frac {5}{3}}}}}$	${\frac {124-7{\sqrt {15}}}{350}}$
	$\pm 1$	${\frac {1}{21}}$

Адаптивный вариант этого алгоритма с двумя внутренними узлами. находится в GNU Octave и MATLAB как quadl и integrate.

Ссылки

Библиография

• Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 25.4, Интеграция». Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. ISBN  978-0-486-61272-0 . LCCN   64-60036 . МР   0167642 . LCCN   65-12253 .
• Андерсон, Дональд Г. (1965). «Квадратурные формулы Гаусса для $\int _{0}^{1}-\ln(x)f(x)dx$. doi Math. Comp . 19 (91): 477–481. : 10.1090 /s0025-5718-1965-0178569-1 .
• Дэнлой, Бернард (1973). «Численное построение квадратурных формул Гаусса для $\int _{0}^{1}(-\log x)x^{\alpha }f(x)dx$ и $\int _{0}^{\infty }E_{m}(x)f(x)dx$". Math. Comp . Том 27, № 124. С. 861–869. doi : 10.1090/S0025-5718-1973-0331730-X . MR   0331730 .
• Итон, Джон В.; Бейтман, Дэвид; Хауберг, Сорен; Вебринг, Рик (2018). «Функции одной переменной (GNU Octave)» . Проверено 28 сентября 2018 г.
• Гандер, Уолтер; Гаучи, Уолтер (2000). «Адаптивная квадратура – ​​новый взгляд» . БИТ Численная математика . 40 (1): 84–101. дои : 10.1023/А:1022318402393 .
• Гаусс, Карл Фридрих (1815). Methodus nova Integrium valores для приближения inveniendi . Комм. Соц. наук. Геттинген Математика Том 3. стр. 29–76. от 1814 г., также в «Сочинениях», том 3, 1876 г., стр. 163–196. Английский перевод Wikisource.
• Гаучи, Уолтер (1968). «Построение квадратурных формул Гаусса – Кристоффеля». Математика. Комп . Том. 22, нет. 102. С. 251–270. дои : 10.1090/S0025-5718-1968-0228171-0 . МР   0228171 .
• Гаучи, Уолтер (1970). «О построении правил квадратур Гаусса из модифицированных моментов». Математика. Комп . Том. 24. С. 245–260. дои : 10.1090/S0025-5718-1970-0285117-6 . МР   0285177 .
• Гаучи, Вальтер (2020). Репозиторий программного обеспечения для гауссовских квадратур и функций Кристоффеля . СИАМ. ISBN  978-1-611976-34-2 .
• Гил, Ампаро; Сегура, Хавьер; Темме, Нико М. (2007), «§5.3: квадратура Гаусса», Численные методы для специальных функций , SIAM, ISBN  978-0-89871-634-4
• Голуб, Джин Х .; Уэлш, Джон Х. (1969). «Расчет по квадратурным правилам Гаусса» . Математика вычислений . 23 (106): 221–230. дои : 10.1090/S0025-5718-69-99647-1 . JSTOR   2004418 .
• Якоби, CGJ (1826 г.). «О новом методе Гаусса приближенного нахождения значений интегралов» . Журнал чистой и прикладной математики . 1 . С. 301–308 и сочинения, том 6. {{cite journal}}: CS1 maint: постскриптум ( ссылка )
• Кабир, Хосейн; Матиколаи, Сайед Амир Хоссейн Хасанпур (2017). «Реализация точного обобщенного гауссова квадратурного решения для поиска упругого поля в однородной анизотропной среде». Журнал Сербского общества вычислительной механики . 11 (1): 11–19. дои : 10.24874/jsscm.2017.11.01.02 .
• Каханер, Дэвид; Молер, Клив ; Нэш, Стивен (1989). Численные методы и программное обеспечение . Прентис Холл . ISBN  978-0-13-627258-8 .
• Лаудадио, Тереза; Мастронарди, Никола; Ван Доорен, Пол (2023). «Вычисление правил квадратур Гаусса с высокой относительной точностью» . Численные алгоритмы . 92 : 767–793. дои : 10.1007/s11075-022-01297-9 .
• Лори, Дирк П. (1999), «Точное восстановление коэффициентов рекурсии из квадратурных формул Гаусса», J. Comput. Прил. Математика. , 112 (1–2): 165–180, doi : 10.1016/S0377-0427(99)00228-9
• Лори, Дирк П. (2001). «Вычисление квадратурных формул типа Гаусса». Дж. Компьютер. Прил. Математика . 127 (1–2): 201–217. Бибкод : 2001JCoAM.127..201L . дои : 10.1016/S0377-0427(00)00506-9 .
• Матворкс (2012). «Численное интегрирование — MATLAB Integral» .
• Писсенс, Р. (1971). «Квадратурные формулы Гаусса для численного интегрирования интеграла Бромвича и обращения преобразования Лапласа». Дж. Инж. Математика . Том. 5, нет. 1. С. 1–9. Бибкод : 1971JEnMa...5....1P . дои : 10.1007/BF01535429 .
• Пресс, WH ; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 4.6. Гауссовы квадратуры и ортогональные полиномы» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8
• Квартерони, Альфио ; Сакко, Риккардо; Салери, Фаусто (2000). Численная математика . Нью-Йорк: Springer Verlag . стр. 425–478. дои : 10.1007/978-3-540-49809-4_10 . ISBN  0-387-98959-5 .
• Ринер, Кордиан; Швайгофер, Маркус (2018). «Подходы к оптимизации квадратуры: новые характеристики гауссовой квадратуры на прямой и квадратуры с небольшим количеством узлов на плоских алгебраических кривых, на плоскости и в более высоких измерениях». Журнал сложности . 45 : 22–54. arXiv : 1607.08404 . дои : 10.1016/j.jco.2017.10.002 .
• Сагар, Робин П. (1991). «Гауссова квадратура для расчета обобщенных интегралов Ферми-Дирака». Вычислить. Физ. Коммун . 66 (2–3): 271–275. Бибкод : 1991CoPhC..66..271S . дои : 10.1016/0010-4655(91)90076-W .
• Стер, Йозеф; Булирш, Роланд (2002), Введение в численный анализ (3-е изд.), Springer , ISBN  978-0-387-95452-3
• Темме, Нико М. (2010), «§3.5(v): Квадратура Гаусса» , в Олвере, Фрэнке В.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .
• Якимив, Э. (1996). «Точное вычисление весов в классических квадратурных правилах Гаусса – Кристоффеля». Дж. Компьютер. Физ . 129 (2): 406–430. Бибкод : 1996JCoPh.129..406Y . дои : 10.1006/jcph.1996.0258 .

Внешние ссылки

• «Квадратурная формула Гаусса» , Математическая энциклопедия , EMS Press , 2001 [1994]
• ALGLIB содержит набор алгоритмов численного интегрирования (на C#/C++/Delphi/Visual Basic/и т.д.)
• Научная библиотека GNU — включает C- версию алгоритмов QUADPACK (см. также Научную библиотеку GNU ).
• От квадратуры Лобатто к постоянной Эйлера e
• Правило интегрирования Гаусса квадратуры - Примечания, PPT, Matlab, Mathematica, Maple, Mathcad в Институте целостных численных методов
• Вайсштейн, Эрик В. «Квадратура Лежандра-Гаусса» . Математический мир .
• Гауссова квадратура Криса Мэйса и Антона Антонова, Демонстрационный проект Wolfram .
• Табличные веса и абсциссы с исходным кодом Mathematica , высокая точность (16 и 256 десятичных знаков). Квадратурные веса и абсциссы Лежандра-Гаусса, от n =2 до n =64, с исходным кодом Mathematica.
• Исходный код Mathematica, распространяемый под лицензией GNU LGPL, для генерации абсцисс и весов для произвольных весовых функций W(x), областей интегрирования и точности.
• Гауссова квадратура в Boost.Math, для произвольной точности и порядка аппроксимации
• Квадратура Гаусса – Кронрода в Boost.Math
• Узлы и веса квадратуры Гаусса. Архивировано 14 апреля 2021 г. на Wayback Machine.