Соотношение сторон

Соотношение сторон фигуры геометрической — это соотношение ее размеров в разных измерениях. Например, соотношение сторон прямоугольника — это отношение его более длинной стороны к более короткой стороне — отношение ширины к высоте. ^[1]^[2] когда прямоугольник ориентирован как « пейзаж ».

Соотношение сторон чаще всего выражается как два целых числа, разделенных двоеточием (x:y), реже — как простая или десятичная дробь . Значения x и y представляют собой не фактическую ширину и высоту, а скорее пропорцию между шириной и высотой. Например, 8:5, 16:10, 1,6:1, 8 ⁄ 5 и 1,6 — это способы представления одного и того же соотношения сторон.

В объектах, имеющих более двух измерений, таких как гиперпрямоугольники , соотношение сторон по-прежнему можно определить как отношение самой длинной стороны к самой короткой стороне.

Приложения и использование

Этот термин чаще всего используется по отношению к:

Графика/изображение
- Соотношение сторон изображения
- Соотношение сторон дисплея
- Размер бумаги
- Стандартные размеры фотоотпечатка
- Форматы кинофильмов
- Стандартный размер объявления
- Соотношение сторон пикселей
- Фотолитография : соотношение сторон травленой или осажденной структуры представляет собой отношение высоты ее вертикальной боковой стенки к ее ширине.
Высокие соотношения сторон HARMST позволяют создавать высокие микроструктуры без наклона.
Код шины
Размер шин
турбокомпрессора Размер крыльчатки
Соотношение сторон крыла самолета или птицы
Астигматизм оптической линзы
Размеры наностержня
Фактор формы (анализ изображений и микроскопия)
Конечно-элементный анализ
Дизайн флага; см. Список соотношений сторон национальных флагов.

Соотношения сторон простых фигур

Прямоугольники

Для прямоугольника соотношение сторон обозначает отношение ширины к высоте прямоугольника. Квадрат . имеет минимально возможное соотношение сторон 1:1

Примеры:

4:3 = 1.3 : Некоторые (не все) компьютерные мониторы 20-го века ( VGA , XGA и т. д.), телевизоры стандартной четкости .
${\sqrt {2}}:1=1.414...$ : международные размеры бумаги ( ISO 216 )
3:2 = 1,5: 35-мм пленка для фотокамеры , iPhone (до iPhone 5 ) отображает
16:10 = 1,6: широко используемые широкоэкранные компьютерные дисплеи ( WXGA ).
Φ:1 = 1,618...: золотое сечение , близкое к 16:10.
5:3 = 1,6 : супер 16 мм , стандартная толщина пленки во многих европейских странах.
16:9 = 1,7 : широкоэкранные телевизоры и большинство ноутбуков.
2:1 = 2: домино
64:27 = 2. 370 : сверхширокоэкранный, 21:9.
32:9 = 3,5 : сверхширокоэкранный режим.

Эллипсы

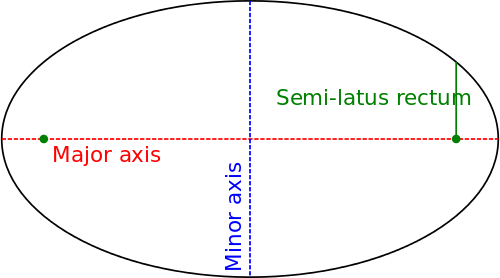
Для эллипса соотношение сторон обозначает отношение большой оси к малой оси . Эллипс с соотношением сторон 1:1 представляет собой круг.

Соотношения сторон общих форм

В геометрии существует несколько альтернативных определений соотношений сторон общих компактов в d-мерном пространстве: ^[3]

Соотношение диаметра и ширины (DWAR) компактного устройства — это отношение его диаметра к ширине. У круга минимальный DWAR равен 1. У квадрата DWAR равен ${\sqrt {2}}$ .
Соотношение сторон кубического объема (CVAR) компактного набора представляет собой корень d -й степени из отношения d -объема наименьшего окружающего d -объему набора -куба, параллельного осям, к собственному d . У квадрата минимальный CVAR равен 1. У круга CVAR равен 1. ${\sqrt {2}}$ . , параллельный оси Прямоугольник ширины W и высоты H , где W > H , имеет CVAR ${\sqrt {W^{2}/WH}}={\sqrt {W/H}}$ .

Если размер d фиксирован, то все разумные определения соотношения сторон эквивалентны с точностью до постоянных коэффициентов.

Обозначения

Соотношения сторон математически выражаются как x : y (произносится как «x-to-y»).

Кинематографические пропорции обычно обозначаются как (округленное) десятичное кратное ширины к единице высоты, тогда как пропорции фотографических и видеографических изображений обычно определяются и обозначаются целыми числами отношения ширины к высоте. В цифровых изображениях существует тонкое различие между соотношением сторон дисплея (изображением в том виде, в котором оно отображается) и хранения соотношением сторон (соотношением размеров пикселей); . Различия см .

См. также

Ссылки

^ Роуз, Маргарет (сентябрь 2005 г.). «Что такое соотношение сторон?» . Что? . ТехТаржет . Проверено 3 февраля 2013 г.
^ Роуз, Маргарет (сентябрь 2002 г.). «Дисплей с широким соотношением сторон» . отображать . E3 отображает . Проверено 18 февраля 2020 г. .
^ Смит, В.Д.; Вормальд, Северная Каролина (1998). «Теоремы и приложения о геометрическом сепараторе». Материалы 39-го ежегодного симпозиума по основам информатики (кат. № 98CB36280) . п. 232. дои : 10.1109/sfcs.1998.743449 . ISBN 0-8186-9172-7 . S2CID 17962961 .

[1] Роуз, Маргарет (сентябрь 2005 г.). «Что такое соотношение сторон?» . Что? . ТехТаржет . Проверено 3 февраля 2013 г.

[2] Роуз, Маргарет (сентябрь 2002 г.). «Дисплей с широким соотношением сторон» . отображать . E3 отображает . Проверено 18 февраля 2020 г. .

[SmithWormald1998-3] Смит, В.Д.; Вормальд, Северная Каролина (1998). «Теоремы и приложения о геометрическом сепараторе». Материалы 39-го ежегодного симпозиума по основам информатики (кат. № 98CB36280) . п. 232. дои : 10.1109/sfcs.1998.743449 . ISBN 0-8186-9172-7 . S2CID 17962961 .

[1]

[2]

[3]

v т и Дроби и соотношения
	Деление и соотношение	Дивиденд ÷ Делитель = Частное
	Фракция	⁠ Числитель / Знаменатель ⁠ = Частное
	алгебраический Аспект Двоичный Продолжение Десятичный Диадический Египетский Золотой Серебро Целое число Нередуцируемый Снижение Просто интонация ЖК-дисплей Музыкальный интервал Размер бумаги Процент Единица