Квантовая система с двумя состояниями

Электрически нейтральный атом серебра проходит через неоднородное магнитное поле эксперимента Штерна-Герлаха , которое разделяется на две части, каждая из которых соответствует одному возможному значению спина самого внешнего электрона атома серебра.

В квантовой механике система с двумя состояниями (также известная как двухуровневая система ) — это квантовая система , которая может существовать в любой квантовой суперпозиции двух независимых (физически различимых) квантовых состояний . Гильбертово пространство, описывающее такую ​​систему, двумерно . Поэтому полноценная основа, охватывающая пространство, будет состоять из двух независимых государств. Любую систему с двумя состояниями также можно рассматривать как кубит .

Системы с двумя состояниями — это простейшие квантовые системы, представляющие интерес, поскольку динамика системы с одним состоянием тривиальна (поскольку других состояний, в которых система может существовать, нет). Математическая основа, необходимая для анализа систем с двумя состояниями, - это линейные дифференциальные уравнения и линейная алгебра двумерных пространств. В результате динамика системы с двумя состояниями может быть решена аналитически без каких-либо приближений. Обычное поведение системы заключается в том, что амплитуда волновой функции колеблется между двумя состояниями.

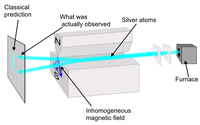
Очень хорошо известным примером системы с двумя состояниями является спин частицы со спином 1/2 , такой как электрон, спин которого может иметь значения + ħ /2 или - ħ /2, где ħ — приведенная постоянная Планка .

Систему двух состояний нельзя использовать для описания поглощения или распада, поскольку такие процессы требуют связи с континуумом. Такие процессы будут включать экспоненциальное затухание амплитуд, но решения двухуровневой системы являются колебательными.

Аналитические решения для энергий стационарного состояния и зависимости от времени

Представительство

Предположим, что двумя доступными базисными состояниями системы являются $|1\rangle$ и $|2\rangle$, в общем случае состояние можно записать как суперпозицию этих двух состояний с амплитудами вероятности $c_{1},c_{2}$, $$|\psi \rangle =c_{1}|1\rangle +c_{2}|2\rangle .$$

Поскольку базисные состояния ортонормированы , $\langle i|j\rangle =\delta _{ij}$ где $i,j\in {1,2}$ и $\delta _{ij}$ это дельта Кронекера , поэтому $c_{i}=\langle i|\psi \rangle$. Эти два комплексных числа можно рассматривать как координаты в двумерном комплексном гильбертовом пространстве . Таким образом, вектор состояния, соответствующий состоянию $|\psi \rangle$ является $$|\psi \rangle \equiv {\begin{pmatrix}\langle 1|\psi \rangle \\\langle 2|\psi \rangle \end{pmatrix}}={\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}=c_{1}{\begin{pmatrix}1\\0\end{pmatrix}}+c_{2}{\begin{pmatrix}0\\1\end{pmatrix}}=\mathbf {c} ,$$ а базисные состояния соответствуют базисным векторам, $$|1\rangle \equiv {\begin{pmatrix}\langle 1|1\rangle \\\langle 2|1\rangle \end{pmatrix}}={\begin{pmatrix}1\\0\end{pmatrix}}$$ и $$|2\rangle \equiv {\begin{pmatrix}\langle 1|2\rangle \\\langle 2|2\rangle \end{pmatrix}}={\begin{pmatrix}0\\1\end{pmatrix}}.$$

Если государство $|\psi \rangle$ нормирован т.е. , норма вектора состояния равна единице, ${|c_{1}|}^{2}+{|c_{2}|}^{2}=1$.

Все наблюдаемые физические величины , такие как энергия, связаны с эрмитовыми операторами . В случае энергии и соответствующего H гамильтониана это означает $$H_{ij}=\langle i|H|j\rangle =\langle j|H|i\rangle ^{*}=H_{ji}^{*},$$ то есть $H_{11}$ и $H_{22}$ реальны, и $H_{12}=H_{21}^{*}$. Таким образом, эти четыре матричных элемента $H_{ij}$ создадим эрмитову матрицу 2×2 , $$\mathbf {H} ={\begin{pmatrix}\langle 1|H|1\rangle &\langle 1|H|2\rangle \\\langle 2|H|1\rangle &\langle 2|H|2\rangle \end{pmatrix}}={\begin{pmatrix}H_{11}&H_{12}\\H_{12}^{*}&H_{22}\end{pmatrix}}.$$

Независимое от времени уравнение Шрёдингера утверждает, что $H|\psi \rangle =E|\psi \rangle$; заменяя $|\psi \rangle$ в терминах базисных состояний сверху и умножив обе части на $\langle 1|$ или $\langle 2|$ образует систему двух линейных уравнений , которую можно записать в матричной форме: $${\begin{pmatrix}H_{11}&H_{12}\\H_{12}^{*}&H_{22}\end{pmatrix}}{\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}=E{\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}},$$ или $\mathbf {Hc} =E\mathbf {c}$ матрицы 2 × 2 что представляет собой проблему собственных значений и собственных векторов . Как упоминалось выше, это уравнение получается в результате включения общего состояния в независимое от времени уравнение Шредингера. Помните, что независимое от времени уравнение Шредингера представляет собой ограничительное условие, используемое для определения собственных состояний. Следовательно, подключая к нему общее состояние, мы видим, какую форму должно принять общее состояние, чтобы стать собственным состоянием. Сделав это и распределив, получим $c_{1}H|1\rangle +c_{2}H|2\rangle =c_{1}E|1\rangle +c_{2}E|2\rangle$, что требует $c_{1}$ или $c_{2}$ быть нулем ( $E$ не может быть равным обоим $\varepsilon _{1}$ и $\varepsilon _{2}$, энергии отдельных состояний, которые по определению различны). После установки $c_{1}$ или $c_{2}$ чтобы быть 0, остается только одно состояние, и $E$ – это энергия выживающего состояния. Этот результат является лишним напоминанием о том, что независимое от времени уравнение Шредингера удовлетворяется только собственными состояниями H, которые (по определению вектора состояния) являются состояниями, в которых все коэффициенты, кроме одного, равны нулю. Теперь, если мы последуем тому же выводу, но прежде чем действовать гамильтонианом на отдельные состояния, мы умножим обе части на $\langle 1|$ или $\langle 2|$, мы получаем систему двух линейных уравнений, которые можно объединить в приведенное выше матричное уравнение. Как и раньше, это может быть удовлетворено только в том случае, если $c_{1}$ или $c_{2}$ равна нулю, и когда это происходит, константа $E$ будет энергией оставшегося состояния. Таким образом, приведенное выше матричное уравнение следует интерпретировать как ограничительное условие на общий вектор состояния, чтобы получить собственный вектор $H$, что в точности аналогично нестационарному уравнению Шрёдингера.

Конечно, в общем случае коммутация матрицы с вектором состояния не приведет к тому же вектору, умноженному на константу E. Для общей справедливости необходимо записать уравнение в виде $${\begin{pmatrix}H_{11}&H_{12}\\H_{12}^{*}&H_{22}\end{pmatrix}}{\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}={\begin{pmatrix}\varepsilon _{1}c_{1}\\\varepsilon _{2}c_{2}\end{pmatrix}},$$ при этом отдельные энергии собственных состояний все еще находятся внутри вектора произведения. В любом случае матрицу Гамильтона можно получить с помощью метода, указанного выше, или с помощью более традиционного метода построения матрицы с использованием граничных условий; в частности, используя требование о том, что, когда он действует на любое базовое состояние, он должен возвращать это состояние, умноженное на энергию этого состояния. (Не существует граничных условий того, как она действует на общее состояние.) В результате получается диагональная матрица, диагональные элементы которой представляют собой энергии собственных состояний, а недиагональные элементы равны нулю. Форма приведенной выше матрицы, в которой используются гамильтонианы, заключенные в бра-кет, является более обобщенной версией этой матрицы.

Можно спросить, зачем записывать матрицу Гамильтона в столь общем виде с гамильтонианами, заключенными в бра-кет, поскольку $H_{ij},i\neq j$ всегда должно быть равно нулю и $H_{ii}$ всегда должно быть равно $\varepsilon _{i}$. Причина в том, что в некоторых более сложных задачах векторы состояния могут не быть собственными состояниями гамильтониана, используемого в матрице. Одно из мест, где это происходит, — это вырожденная теория возмущений , где недиагональные элементы не равны нулю, пока проблема не будет решена путем диагонализации .

Из-за герметичности $\mathbf {H}$ собственные значения действительны; или, скорее, наоборот, именно требование реальности энергий подразумевает герметичность $\mathbf {H}$. Собственные векторы представляют собой стационарные состояния , т. е. такие, для которых абсолютные величины квадратов амплитуд вероятностей не меняются со временем.

Собственные значения гамильтониана

Наиболее общая форма эрмитовой матрицы 2 × 2, такой как гамильтониан системы с двумя состояниями, определяется выражением $$\mathbf {H} ={\begin{pmatrix}\varepsilon _{1}&\beta -i\gamma \\\beta +i\gamma &\varepsilon _{2}\end{pmatrix}},$$ где $\varepsilon _{1},\varepsilon _{2},\beta$ и γ — действительные числа с единицами энергии. Разрешенные уровни энергии системы, а именно собственные значения матрицы Гамильтона, находятся обычным способом.

Эквивалентно, эту матрицу можно разложить как: $$\mathbf {H} =\alpha \cdot \sigma _{0}+\beta \cdot \sigma _{1}+\gamma \cdot \sigma _{2}+\delta \cdot \sigma _{3}={\begin{pmatrix}\alpha +\delta &\beta -i\gamma \\\beta +i\gamma &\alpha -\delta \end{pmatrix}}.$$ Здесь, ${\textstyle \alpha ={\frac {1}{2}}\left(\varepsilon _{1}+\varepsilon _{2}\right)}$ и ${\textstyle \delta ={\frac {1}{2}}\left(\varepsilon _{1}-\varepsilon _{2}\right)}$ являются действительными числами. Матрица $\sigma _{0}$ - единичная матрица 2 × 2 и матрицы $\sigma _{k}$ с $k=1,2,3$ — матрицы Паули . Такая декомпозиция упрощает анализ системы, особенно в нестационарном случае, когда значения $\alpha ,\beta ,\gamma$ и $\delta$ являются константами.

Гамильтониан можно далее сократить как $$\mathbf {H} =\alpha \cdot \sigma _{0}+\mathbf {r} \cdot {\boldsymbol {\sigma }}.$$

Вектор $\mathbf {r}$ дается $(\beta ,\gamma ,\delta )$ и $\sigma$ дается $(\sigma _{1},\sigma _{2},\sigma _{3})$. Это представление упрощает анализ эволюции системы во времени и его легче использовать с другими специализированными представлениями, такими как сфера Блоха .

системы с двумя состояниями Если независимый от времени гамильтониан H определен, как указано выше, то его собственные значения определяются выражением $E_{\pm }=\alpha \pm |\mathbf {r} |$. Очевидно, α — средняя энергия двух уровней, норма а $\mathbf {r}$ это раскол между ними. Соответствующие собственные векторы обозначаются как $|+\rangle$ и $|-\rangle$.

Зависимость от времени

Теперь мы предполагаем, что амплитуды вероятности зависят от времени, хотя базисные состояния — нет. Зависящее от времени уравнение Шредингера гласит: ${\textstyle i\hbar \partial _{t}|\psi \rangle =H|\psi \rangle }$, и действуя, как и раньше (заменив $|\psi \rangle$ и предварительно умножив на $\langle 1|,\langle 2|$ снова дает пару связанных линейных уравнений, но на этот раз это уравнения в частных производных первого порядка: ${\textstyle i\hbar \partial _{t}\mathbf {c} =\mathbf {Hc} }$. Если $\mathbf {H}$ не зависит от времени, существует несколько подходов к нахождению зависимости от времени. $c_{1},c_{2}$, такие как обычные режимы . В результате $$\mathbf {c} (t)=e^{-i\mathbf {H} t/\hbar }\mathbf {c} _{0}=\mathbf {U} (t)\mathbf {c} _{0}.$$ где $\mathbf {c} _{0}=\mathbf {c} (0)$ это вектор состояния в $t=0$. Здесь экспоненту матрицы можно найти путем разложения в ряд. Матрица $\mathbf {U} (t)$ называется матрицей временной эволюции (которая состоит из матричных элементов соответствующего оператора временной эволюции $U(t)$). Легко доказывается, что $\mathbf {U} (t)$ является унитарным , то есть $\mathbf {U} ^{\dagger }\mathbf {U} =1$.

Можно показать, что $$\mathbf {U} (t)=e^{-i\mathbf {H} t/\hbar }=e^{-i\alpha t/\hbar }\left(\cos \left({\frac {|\mathbf {r} |}{\hbar }}t\right)\sigma _{0}-i\sin \left({\frac {|\mathbf {r} |}{\hbar }}t\right){\hat {r}}\cdot {\boldsymbol {\sigma }}\right),$$ где ${\textstyle {\hat {r}}={\frac {\mathbf {r} }{|\mathbf {r} |}}.}$

Другими словами, когда кто-то заменяет базис собственными векторами гамильтониана, если базис утверждает $|1\rangle ,|2\rangle$ выбраны в качестве собственных векторов, то $\epsilon _{1}=H_{11}=\langle 1|H|1\rangle =E_{1}\langle 1|1\rangle =E_{1}$ и $\beta +i\gamma =H_{21}=\langle 2|H|1\rangle =E_{1}\langle 2|1\rangle =0$ и поэтому гамильтониан диагональен, т. е. $|\mathbf {r} |=\delta$ и имеет форму, $$\mathbf {H} ={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}.$$

Теперь унитарный оператор эволюции по времени $U$ легко видеть, что оно дается формулой: $$\mathbf {U} (t)=e^{-i\mathbf {H} t/\hbar }={\begin{pmatrix}e^{-iE_{1}t/\hbar }&0\\0&e^{-iE_{2}vt/\hbar }\end{pmatrix}}=e^{-i\alpha t/\hbar }{\begin{pmatrix}e^{-i\delta t/\hbar }&0\\0&e^{i\delta t/\hbar }\end{pmatrix}}=e^{-i\alpha t/\hbar }\left(\cos \left({\frac {\delta }{\hbar }}t\right)\sigma _{0}-i\sin \left({\frac {\delta }{\hbar }}t\right){\boldsymbol {\sigma }}_{3}\right).$$ $e^{-i\alpha t/\hbar }$ Фактор просто вносит вклад в общую фазу оператора, и его обычно можно игнорировать, чтобы получить новый оператор временной эволюции, который физически неотличим от исходного оператора. Более того, любое возмущение системы (которое будет иметь тот же вид, что и гамильтониан) может быть добавлено к системе в собственном базисе невозмущенного гамильтониана и проанализировано так же, как указано выше. Следовательно, для любого возмущения новые собственные векторы возмущенной системы могут быть решены точно, как указано во введении.

Формула Раби для статического возмущения

Предположим, что система стартует в одном из базисных состояний в момент $t=0$, сказать $|1\rangle$ так что ${\textstyle \mathbf {c} _{0}={\begin{pmatrix}1\\0\end{pmatrix}}}$, и нас интересует вероятность занятия каждого из базисных состояний как функция времени, когда $\mathbf {H}$ — независимый от времени гамильтониан. $$\mathbf {c} (t)=\mathbf {U} (t)\mathbf {c} _{0}={\begin{pmatrix}U_{11}(t)&U_{12}(t)\\U_{21}(t)&U_{22}(t)\end{pmatrix}}{\begin{pmatrix}1\\0\end{pmatrix}}={\begin{pmatrix}U_{11}(t)\\U_{21}(t)\end{pmatrix}}.$$

Вероятность занятия состояния i равна $P_{i}(t)=|c_{i}(t)|^{2}=|U_{i1}(t)|^{2}$. В случае начального состояния $P_{1}(t)=|c_{1}(t)|^{2}=|U_{11}(t)|^{2}$, и сверху, $$U_{11}(t)=e^{\frac {-i\alpha t}{\hbar }}\left(\cos \left({\frac {|\mathbf {r} |}{\hbar }}t\right)-i\sin \left({\frac {|\mathbf {r} |}{\hbar }}t\right){\frac {\delta }{|\mathbf {r} |}}\right).$$ Следовательно, $$P_{1}(t)=\cos ^{2}(\Omega t)+\sin ^{2}(\Omega t){\frac {\Delta ^{2}}{\Omega ^{2}}}.$$

Очевидно, $P_{1}(0)=1$ из-за начального состояния. Частота $$\Omega ={\frac {|\mathbf {r} |}{\hbar }}={\frac {1}{\hbar }}{\sqrt {\beta ^{2}+\gamma ^{2}+\delta ^{2}}}={\sqrt {|\Omega _{R}|^{2}+\Delta ^{2}}}$$ называется обобщенной частотой Раби, $\Omega _{R}=(\beta +i\gamma )/\hbar$ называется частотой Раби, а $\Delta =\delta /\hbar$ называется отстройкой.

При нулевой расстройке $P_{1}(t)=\cos ^{2}(|\Omega _{R}|t)$, т. е. происходит переход Раби от гарантированной оккупации государства 1 к гарантированной оккупации государства 2 и обратно к состоянию 1 и т. д. с частотой $|\Omega _{R}|$. По мере увеличения отстройки от нуля частота флопа увеличивается (до Ω ), а амплитуда возбуждения электрона уменьшается до $\Omega ^{2}/\Delta ^{2}$.

О гамильтонианах, индуцированных световыми волнами, зависящих от времени, см. в статьях о цикле Раби и приближении вращающихся волн .

Некоторые важные системы с двумя государствами

Прецессия в поле

Рассмотрим случай частицы со спином 1/2 в магнитном поле. $\mathbf {B} =B\mathbf {\hat {n}}$. Гамильтониан взаимодействия для этой системы имеет вид $$H=-{\boldsymbol {\mu }}\cdot \mathbf {B} =-\mu {\boldsymbol {\sigma }}\cdot \mathbf {B} ,$$ где $\mu$ частицы - величина магнитного момента и ${\boldsymbol {\sigma }}$ — вектор матриц Паули . Решение нестационарного уравнения Шрёдингера $H\psi =i\hbar \partial _{t}\psi$ урожайность $$\psi (t)=e^{i\omega t{\boldsymbol {\sigma }}\cdot \mathbf {\hat {n}} }\psi (0),$$ где $\omega =\mu B/\hbar$ и $e^{i\omega t{\boldsymbol {\sigma }}\cdot \mathbf {\hat {n}} }=\cos {\left(\omega t\right)}I+i\;\mathbf {\hat {n}} \cdot {\boldsymbol {\sigma }}\sin {\left(\omega t\right)}$. Физически это соответствует вектору Блоха , прецессирующему вокруг $\mathbf {\hat {n}}$ с угловой частотой $2\omega$. Без ограничения общности предположим, что поле представляет собой однородные точки в $\mathbf {\hat {z}}$, так что оператор эволюции во времени задается как $$e^{i\omega t{\boldsymbol {\sigma }}\cdot \mathbf {\hat {n}} }={\begin{pmatrix}e^{i\omega t}&0\\0&e^{-i\omega t}\end{pmatrix}}.$$

Видно, что такой оператор временной эволюции, действующий на общее спиновое состояние частицы со спином 1/2, приведет к прецессии вокруг оси, определяемой приложенным магнитным полем (это квантовомеханический эквивалент ларморовской прецессии )

Описанный выше метод можно применить к анализу любой общей системы с двумя состояниями, которая взаимодействует с некоторым полем (эквивалентным магнитному полю в предыдущем случае), если взаимодействие задается подходящим членом связи, аналогичным магнитному моменту. . Прецессию вектора состояния (которая не обязательно должна быть физическим вращением, как в предыдущем случае) можно рассматривать как прецессию вектора состояния на сфере Блоха .

Представление на сфере Блоха вектора состояния $\psi (0)$ будет просто вектором значений ожидания $\mathbf {R} =\left(\langle \sigma _{x}\rangle ,\langle \sigma _{y}\rangle ,\langle \sigma _{z}\rangle \right)$. В качестве примера рассмотрим вектор состояния $\psi (0)$ это нормализованная суперпозиция $\left|\uparrow \right\rangle$ и $\left|\downarrow \right\rangle$, то есть вектор, который можно представить в виде $\sigma _{z}$ основе как $$\psi (0)={\frac {1}{\sqrt {2}}}{\begin{pmatrix}1\\1\end{pmatrix}}$$

Компоненты $\psi (t)$ на сфере Блоха будет просто $\mathbf {R} =\left(\cos {2\omega t},-\sin {2\omega t},0\right)$. Это единичный вектор, который начинает указывать вдоль $\mathbf {\hat {x}}$ и прецессирует вокруг $\mathbf {\hat {z}}$ левым способом. В общем, вращением вокруг $\mathbf {\hat {z}}$, любой вектор состояния $\psi (0)$ может быть представлено как $a\left|\uparrow \right\rangle +b\left|\downarrow \right\rangle$ с реальными коэффициентами $a$ и $b$. Такой вектор состояния соответствует вектору Блоха в плоскости xz, составляющему угол $\tan(\theta /2)=b/a$ с осью z . Этот вектор будет прецессировать вокруг $\mathbf {\hat {z}}$. Теоретически, позволяя системе взаимодействовать с полем определенного направления и силы в течение точного времени, можно получить любую ориентацию вектора Блоха , что эквивалентно получению любой сложной суперпозиции. Это основа многочисленных технологий, включая квантовые вычисления и МРТ .

Эволюция во нестационарном поле: ядерный магнитный резонанс.

Ядерный магнитный резонанс (ЯМР) является важным примером динамики систем с двумя состояниями, поскольку он включает точное решение гамильтониана, зависящего от времени. Явление ЯМР достигается путем помещения ядра в сильное статическое поле B ₀ («удерживающее поле») и последующего приложения слабого поперечного поля B ₁ , которое колеблется на некоторой радиочастоте ω _r . Явно рассмотрим частицу со спином 1/2 в удерживающем поле. $B_{0}\mathbf {\hat {z}}$ и поперечное радиочастотное поле B _1, вращающееся в плоскости xy вправо вокруг B ₀ : $$\mathbf {B} ={\begin{pmatrix}B_{1}\cos \omega _{\mathrm {r} }t\\B_{1}\sin \omega _{\mathrm {r} }t\\B_{0}\end{pmatrix}}.$$

Как и в случае свободной прецессии, гамильтониан имеет вид $H=-\mu {\boldsymbol {\sigma }}\cdot \mathbf {B}$и эволюция вектора состояния $\psi (t)$ находится путем решения нестационарного уравнения Шредингера $H\psi =i\hbar \,\partial \psi /\partial t$. После некоторых манипуляций (приведенных в свернутом разделе ниже) можно показать, что уравнение Шредингера принимает вид $${\frac {\partial \psi }{\partial t}}=i\left(\omega _{1}\sigma _{x}+\left(w_{0}+{\frac {\omega _{r}}{2}}\right)\sigma _{z}\right)\psi ,$$ где $\omega _{0}=\mu B_{0}/\hbar$ и $\omega _{1}=\mu B_{1}/\hbar$.

Как и в предыдущем разделе, решение этого уравнения имеет вектор Блоха, прецессирующий вокруг $(\omega _{1},0,\omega _{0}+\omega _{r}/2)$ с частотой, вдвое превышающей величину вектора. Если $\omega _{0}$ достаточно сильно, некоторая часть спинов будет направлена ​​прямо вниз до появления вращающегося поля. Если угловая частота вращающегося магнитного поля выбрана такой, что $\omega _{r}=-2\omega _{0}$, во вращающейся системе отсчета вектор состояния будет прецессировать вокруг ${\hat {x}}$ с частотой $2\omega _{1}$, и, таким образом, будет переворачиваться снизу вверх, высвобождая энергию в виде обнаруживаемых фотонов. Это фундаментальная основа ЯМР , которая на практике достигается путем сканирования. $\omega _{r}$ до тех пор, пока не будет найдена резонансная частота, после чего образец начнет излучать свет. используется приближение вращающейся волны Подобные расчеты производятся в атомной физике, и в случае, когда поле не вращается, а колеблется с комплексной амплитудой, для получения таких результатов .

Вывод приведенного выше выражения для уравнения ЯМР Шредингера

Здесь уравнение Шредингера имеет вид $$-\mu {\boldsymbol {\sigma }}\cdot \mathbf {B} \psi =i\hbar {\frac {\partial \psi }{\partial t}}.$$

Разложение скалярного произведения и деление на $i\hbar$ урожайность $${\frac {\partial \psi }{\partial t}}=i\left(\omega _{1}\sigma _{x}\cos {\omega _{r}t}+\omega _{1}\sigma _{y}\sin {\omega _{r}t}+\omega _{0}\sigma _{z}\right)\psi .$$

Чтобы убрать зависимость от времени из задачи, волновая функция преобразуется согласно $\psi \rightarrow e^{-i\sigma _{z}\omega _{r}t/2}\psi$. Зависящее от времени уравнение Шредингера принимает вид $$-i\sigma _{z}{\frac {\omega _{r}}{2}}e^{-i\sigma _{z}\omega _{r}t/2}\psi +e^{-i\sigma _{z}\omega _{r}t/2}{\frac {\partial \psi }{\partial t}}=i\left(\omega _{1}\sigma _{x}\cos {\omega _{r}t}+\omega _{1}\sigma _{y}\sin {\omega _{r}t}+\omega _{0}\sigma _{z}\right)e^{-i\sigma _{z}\omega _{r}t/2}\psi ,$$ что после некоторой перестановки дает $${\frac {\partial \psi }{\partial t}}=ie^{i\sigma _{z}\omega _{r}t/2}\left(\omega _{1}\sigma _{x}\cos {\omega _{r}t}+\omega _{1}\sigma _{y}\sin {\omega _{r}t}+\left(\omega _{0}+{\frac {\omega _{r}}{2}}\right)\sigma _{z}\right)e^{-i\sigma _{z}\omega _{r}t/2}\psi$$

Оценка каждого члена в правой части уравнения $$e^{i\sigma _{z}\omega _{r}t/2}\sigma _{x}e^{-i\sigma _{z}\omega _{r}t/2}={\begin{pmatrix}e^{i\omega _{r}t/2}&0\\0&e^{-i\omega _{r}t/2}\end{pmatrix}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}{\begin{pmatrix}e^{-i\omega _{r}t/2}&0\\0&e^{i\omega _{r}t/2}\end{pmatrix}}={\begin{pmatrix}0&e^{i\omega _{r}t}\\e^{-i\omega _{r}t}&0\end{pmatrix}}$$ $$e^{i\sigma _{z}\omega _{r}t/2}\sigma _{y}e^{-i\sigma _{z}\omega _{r}t/2}={\begin{pmatrix}e^{i\omega _{r}t/2}&0\\0&e^{-i\omega _{r}t/2}\end{pmatrix}}{\begin{pmatrix}0&-i\\i&0\end{pmatrix}}{\begin{pmatrix}e^{-i\omega _{r}t/2}&0\\0&e^{i\omega _{r}t/2}\end{pmatrix}}={\begin{pmatrix}0&-ie^{i\omega _{r}t}\\ie^{-i\omega _{r}t}&0\end{pmatrix}}$$ $$e^{i\sigma _{z}\omega _{r}t/2}\sigma _{z}e^{-i\sigma _{z}\omega _{r}t/2}={\begin{pmatrix}e^{i\omega _{r}t/2}&0\\0&e^{-i\omega _{r}t/2}\end{pmatrix}}{\begin{pmatrix}1&0\\0&-1\end{pmatrix}}{\begin{pmatrix}e^{-i\omega _{r}t/2}&0\\0&e^{i\omega _{r}t/2}\end{pmatrix}}=\sigma _{z}$$

Уравнение теперь читается $${\frac {\partial \psi }{\partial t}}=i\left(\omega _{1}{\begin{pmatrix}0&e^{i\omega _{r}t}\left(\cos {\omega _{r}t}-i\sin {\omega _{r}t}\right)\\e^{-i\omega _{r}t}\left(\cos {\omega _{r}t}+i\sin {\omega _{r}t}\right)&0\end{pmatrix}}+\left(w_{0}+{\frac {\omega _{r}}{2}}\right)\sigma _{z}\right)\psi ,$$ что по тождеству Эйлера становится $${\frac {\partial \psi }{\partial t}}=i\left(\omega _{1}\sigma _{x}+\left(w_{0}+{\frac {\omega _{r}}{2}}\right)\sigma _{z}\right)\psi$$

Связь с уравнениями Блоха

Оптические уравнения Блоха для совокупности частиц со спином 1/2 могут быть получены из зависящего от времени уравнения Шредингера для двухуровневой системы. Начиная с ранее установленного гамильтониана $i\hbar \partial _{t}\psi =-\mu {\boldsymbol {\sigma }}\cdot \mathbf {B} \psi$, его можно записать в виде суммирования после некоторой перестановки как $${\frac {\partial \psi }{\partial t}}=i{\frac {\mu }{\hbar }}\sigma _{i}B_{i}\psi$$

Умножение на матрицу Паули $\sigma _{i}$ и сопряженное транспонирование волновой функции с последующим разложением произведения двух матриц Паули дает $$\psi ^{\dagger }\sigma _{j}{\frac {\partial \psi }{\partial t}}=i{\frac {\mu }{\hbar }}\psi ^{\dagger }\sigma _{j}\sigma _{i}B_{i}\psi =i{\frac {\mu }{\hbar }}\psi ^{\dagger }\left(I\delta _{ij}-i\sigma _{k}\varepsilon _{ijk}\right)B_{i}\psi ={\frac {\mu }{\hbar }}\psi ^{\dagger }\left(iI\delta _{ij}+\sigma _{k}\varepsilon _{ijk}\right)B_{i}\psi$$

Добавление этого уравнения к его собственному сопряженному транспонированию дает левую часть формы $$\psi ^{\dagger }\sigma _{j}{\frac {\partial \psi }{\partial t}}+{\frac {\partial \psi ^{\dagger }}{\partial t}}\sigma _{j}\psi ={\frac {\partial \left(\psi ^{\dagger }\sigma _{j}\psi \right)}{\partial t}}$$

И правая часть формы $${\frac {\mu }{\hbar }}\psi ^{\dagger }\left(iI\delta _{ij}+\sigma _{k}\varepsilon _{ijk}\right)B_{i}\psi +{\frac {\mu }{\hbar }}\psi ^{\dagger }\left(-iI\delta _{ij}+\sigma _{k}\varepsilon _{ijk}\right)B_{i}\psi ={\frac {2\mu }{\hbar }}\left(\psi ^{\dagger }\sigma _{k}\psi \right)B_{i}\varepsilon _{ijk}$$

Как упоминалось ранее, математическое ожидание каждой матрицы Паули является компонентом вектора Блоха , $\langle \sigma _{i}\rangle =\psi ^{\dagger }\sigma _{i}\psi =R_{i}$. Приравнивая левую и правую части и отмечая, что ${\frac {2\mu }{\hbar }}$ это гиромагнитное отношение $\gamma$, дает другой вид уравнений движения вектора Блоха $${\frac {\partial R_{j}}{\partial t}}=\gamma R_{k}B_{i}\varepsilon _{kij}$$ где тот факт, что $\varepsilon _{ijk}=\varepsilon _{kij}$ был использован. В векторной форме эти три уравнения можно выразить через векторное произведение $${\frac {\partial \mathbf {R} }{\partial t}}=\gamma \mathbf {R} \times \mathbf {B}$$ Классически это уравнение описывает динамику спина в магнитном поле. Идеальный магнит состоит из набора одинаковых спинов, ведущих себя независимо, и, следовательно, общая намагниченность $\mathbf {M}$ пропорционален вектору Блоха $\mathbf {R}$. Все, что осталось для получения окончательной формы оптических уравнений Блоха, — это учет феноменологических релаксационных членов.

И наконец, приведенное выше уравнение можно вывести, рассматривая временную эволюцию оператора углового момента в картине Гейзенберга . $$i\hbar {\frac {d\sigma _{j}}{dt}}=\left[\sigma _{j},H\right]=\left[\sigma _{j},-\mu \sigma _{i}B_{i}\right]=-\mu \left(\sigma _{j}\sigma _{i}B_{i}-\sigma _{i}\sigma _{j}B_{i}\right)=\mu [\sigma _{i},\sigma _{j}]B_{i}=2\mu i\varepsilon _{ijk}\sigma _{k}B_{i}$$

В сочетании с тем, что $\mathbf {R} _{i}=\langle \sigma _{i}\rangle$, это уравнение является тем же уравнением, что и раньше.

Срок действия

Системы с двумя состояниями — это простейшие нетривиальные квантовые системы, встречающиеся в природе, но упомянутые выше методы анализа справедливы не только для простых систем с двумя состояниями. Любую общую квантовую систему с несколькими состояниями можно рассматривать как систему с двумя состояниями, если интересующая наблюдаемая система имеет два собственных значения. Например, частица со спином 1/2 в действительности может иметь дополнительные поступательные или даже вращательные степени свободы, но эти степени свободы не имеют отношения к предыдущему анализу. Математически пренебрегаемые степени свободы соответствуют вырождению собственных значений спина.

Другой случай, когда эффективный формализм двух состояний справедлив, — это когда рассматриваемая система имеет два уровня, которые эффективно отделены от системы. Так обстоит дело при анализе спонтанного или вынужденного излучения света атомами и зарядовыми кубитами . При этом следует иметь в виду, что возмущения (взаимодействия с внешним полем) находятся в нужном диапазоне и не вызывают переходов в состояния, отличные от интересующих.

Значение и другие примеры

С педагогической точки зрения формализм двух состояний является одним из самых простых математических методов, используемых для анализа квантовых систем. Его можно использовать для иллюстрации фундаментальных квантово-механических явлений, таких как интерференция частиц с состояниями поляризации фотона, но также и более сложные явления, такие как осцилляции нейтрино или осцилляции нейтрального K-мезона .

Формализм двух состояний можно использовать для описания простого смешивания состояний, которое приводит к таким явлениям, как стабилизация резонанса и другим симметриям, связанным с пересечением уровней . Подобные явления имеют широкое применение в химии. Явления, имеющие огромное промышленное применение, такие как мазер и лазер, можно объяснить с помощью формализма двух состояний.

Формализм двух состояний также лежит в основе квантовых вычислений . Кубиты , являющиеся строительными блоками квантового компьютера, представляют собой не что иное, как системы с двумя состояниями. Любая квантовая вычислительная операция — это унитарная операция, вращающая вектор состояния на сфере Блоха.

Дальнейшее чтение

• Трактовка формализма двух состояний, представленная в третьем томе « Фейнмановских лекций по физике» .
• Конспекты лекций:
• из курса «Квантовая механика II» , предлагаемого в Массачусетском технологическом институте , http://web.mit.edu/8.05/handouts/Twostates_03.pdf.
  • из того же курса, посвященного колебаниям нейтральных частиц, http://web.mit.edu/8.05/handouts/nukaon_07.pdf
  • из курса «Квантовая механика I» , предлагаемого в TIFR , http://theory.tifr.res.in/~sgupta/courses/qm2013/hand4.pdf охватывает основные математические аспекты.
  • http://theory.tifr.res.in/~sgupta/courses/qm2013/hand5.pdf ; из того же курса рассматриваются некоторые физические двухгосударственные системы и другие важные аспекты формализма.
  • математические расчеты в начальном разделе выполнены аналогично этим примечаниям http://www.math.columbia.edu/~woit/QM/qubit.pdf , которые взяты из курса «Квантовая механика для математиков», предлагаемого в Колумбийском университете. .
  • книжная версия того же самого; http://www.math.columbia.edu/~woit/QM/qmbook.pdf
  • Двухгосударственные системы и две сферы, Р. Дж. Плимен, Il Nuovo Cimento B 13 (1973) 55-58

См. также

• Цикл Раби
• Дублет
• Ядерный магнитный резонанс
• Квантовая оптика
• Кубит