Роллинг

Вращение - это тип движения , который сочетает в себе вращение (обычно осесимметричного объекта) и перемещение этого объекта относительно поверхности (либо одно, либо другое движение), так что, если существуют идеальные условия, они находятся в контакте. друг с другом, не скользя .

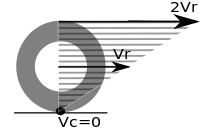
Прокатка без скольжения называется чистой прокаткой . По определению, скольжение отсутствует, когда существует система отсчета , в которой все точки контакта на катящемся объекте имеют ту же скорость, что и их аналоги на поверхности, по которой катится объект; в частности, для системы отсчета, в которой катящаяся плоскость покоится (см. анимацию), мгновенная скорость всех точек контакта (например, отрезка образующей цилиндра) катящегося объекта равна нулю.

На практике из-за небольших деформаций вблизи зоны контакта происходит некоторое скольжение и диссипация энергии. Тем не менее, результирующее сопротивление качению намного ниже, чем трение скольжения , и, таким образом, катящимся объектам обычно требуется гораздо меньше энергии для перемещения, чем скользящим. В результате такие объекты будут легче двигаться, если на них действует сила с компонентом, расположенным вдоль поверхности, например сила тяжести на наклонной поверхности, ветер, толкание, притяжение или крутящий момент двигателя. В отличие от цилиндрических осесимметричных объектов, движение конуса таково, что при качении по плоской поверхности его центр тяжести совершает круговое , а не линейное движение . Катящиеся объекты не обязательно аксиально-симметричны. Двумя хорошо известными неосесимметричными роликами являются треугольник Рело и тела Мейснера . Олоид , и сферикон относятся к особому семейству развертывающихся роликов которые развивают при скатывании по плоской плоскости всю свою поверхность. Объекты с углами, например игральную кость , катите ее последовательными вращениями вокруг края или угла, соприкасающегося с поверхностью. Конструкция особой поверхности позволяет даже идеальному квадратному колесу катиться с центром тяжести, находящимся на постоянной высоте над базовой плоскостью.

Приложения

Большинство наземных транспортных средств используют колеса и, следовательно, перекатываются для перемещения. Скольжение должно быть минимальным (приближенным к чистому качению), в противном случае может произойти потеря управления и авария. Это может произойти, если дорога покрыта снегом, песком или маслом, при повороте на высокой скорости или при попытке резко затормозить или ускориться.

Одним из наиболее практических применений объектов качения является использование подшипников качения , например шарикоподшипников , во вращающихся устройствах. Изготовленные из металла тела качения обычно заключены между двумя кольцами, которые могут вращаться независимо друг от друга. В большинстве механизмов внутреннее кольцо прикреплено к неподвижному валу (или оси). Таким образом, пока внутреннее кольцо неподвижно, внешнее кольцо может свободно перемещаться с минимальным трением . Это основа, на которой работают почти все двигатели (например, в потолочных вентиляторах, автомобилях, дрелях и т. д.). Альтернативно, внешнее кольцо может быть прикреплено к фиксированному опорному кронштейну, позволяя внутреннему кольцу поддерживать ось, обеспечивая свободу вращения оси . Величина трения деталей механизма зависит от качества шарикоподшипников и количества смазки в механизме.

часто используются в качестве средств транспортировки . Катящиеся предметы также Один из самых простых способов — разместить (обычно плоский) объект на ряде расположенных в ряд роликов или колес . Объект на колесах можно перемещать по ним по прямой, при условии, что колеса постоянно заменяются спереди (см. историю подшипников ). Этот примитивный метод транспортировки эффективен, когда нет другой техники. Сегодня наиболее практичным применением объектов на колесах являются автомобили , поезда и другие средства передвижения людей.

Прокатка применяется для приложения нормальных сил к движущейся линии контакта в различных процессах, например в металлообработке , полиграфии , производстве резины , покраске .

Твердые тела

Скорости точек катящегося объекта равны скоростям вращения вокруг точки контакта.

Простейшим случаем качения является катание твердого тела без скольжения по плоской поверхности с осью, параллельной поверхности (или, что то же самое: перпендикулярно нормали к поверхности ).

Траектория любой точки — трохоида ; в частности, траектория любой точки оси объекта представляет собой линию, а траектория любой точки обода объекта — циклоиду .

Скорость любой точки катящегося объекта определяется выражением $\mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {r}$ , где $\mathbf {r}$ — смещение между частицей и точкой контакта (или линией) катящегося объекта с поверхностью, а ω — вектор угловой скорости . ^{[ 1 ]} Таким образом, несмотря на то, что качение отличается от вращения вокруг неподвижной оси , мгновенная скорость всех частиц катящегося объекта такая же, как если бы он вращался вокруг оси, проходящей через точку контакта с одинаковой угловой скоростью.

Любая точка катящегося объекта, расположенная дальше от оси, чем точка контакта, будет временно перемещаться противоположно направлению общего движения, когда она находится ниже уровня поверхности качения (например, любая точка в части фланца катящегося объекта). колесо поезда, находящееся под рельсом).

Энергия

Поскольку кинетическая энергия полностью зависит от массы и скорости объекта, приведенный выше результат можно использовать вместе с теоремой о параллельной оси , чтобы получить кинетическую энергию, связанную с простым вращением.

K_{\text{rolling}}=K_{\text{translation}}+K_{\text{rotation}}

Вывод Further information: Rotation around a fixed axis Let $r$ be the distance between the center of mass and the point of contact; when the surface is flat, this is the radius of the object around its widest cross section. Since the center of mass has an immediate velocity as if it was rotating around the point of contact, its velocity is $v_{\text{c.o.m.}}=r\omega$ . Due to symmetry, the object center of mass is a point in its axis. Let $I_{\text{rotation}}$ be inertia of pure rotation around the axis of symmetry, then according to the parallel axis theorem, the rotational inertia associated with rolling is $I_{\text{rolling}}=mr^{2}+I_{\text{rotation}}$ (same as the rotational inertia of pure rotation around the point of contact). Using the general formula for kinetic energy of rotation, we have: ${\begin{aligned}K_{\text{rolling}}&={\frac {1}{2}}I_{\text{rolling}}\omega ^{2}\\&={\frac {1}{2}}mr^{2}\omega ^{2}+{\frac {1}{2}}I_{\text{rotation}}\omega ^{2}\\&={\frac {1}{2}}m(r\omega )^{2}+{\frac {1}{2}}I_{\text{rotation}}\omega ^{2}\\&={\frac {1}{2}}mv_{\text{c.o.m.}}^{2}+{\frac {1}{2}}I_{\text{rotation}}\omega ^{2}\\&=K_{\text{translation}}+K_{\text{rotation}}\\\end{aligned}}$

Силы и ускорение

Дифференцируя связь между линейной и угловой скоростью , $v_{\text{c.o.m.}}=r\omega$ , по времени дает формулу, связывающую линейное и угловое ускорение $a=r\alpha$ . Применяя второй закон Ньютона :

a={\frac {F_{\text{net}}}{m}}=r\alpha ={\frac {r\tau }{I}}.

Отсюда следует, что для ускорения объекта как чистая сила, так и крутящий момент необходимы . Когда на систему катящегося объекта-поверхности действует внешняя сила без крутящего момента, в точке контакта между поверхностью и катящимся объектом будет действовать касательная сила, которая обеспечивает необходимый крутящий момент, пока движение представляет собой чистое качение; эта сила обычно представляет собой статическое трение , например, между дорогой и колесом или между дорожкой для боулинга и шаром для боулинга. Когда статического трения недостаточно, трение становится динамическим и происходит проскальзывание. Тангенциальная сила противоположна по направлению внешней силе и, следовательно, частично ее нейтрализует. Результирующая чистая сила и ускорение равны:

{\begin{aligned}F_{\text{net}}&={\frac {F_{\text{external}}}{1+{\frac {I}{mr^{2}}}}}={\frac {F_{\text{external}}}{1+\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}}}\\a&={\frac {F_{\text{external}}}{m+{\frac {I}{r^{2}}}}}\end{aligned}}

Вывод

Assume that the object experiences an external force

F_{\text{external}}

which exerts no torque (it has 0 moment arm), static friction at the point of contact (

F_{\text{friction}}

) provides the torque and the other forces involved cancel.

F_{\text{friction}}

is tangential to the object and surface at the point of contact and opposite in direction to

F_{\text{external}}

. Using the sign convention by which this force is positive, the net force is:

F_{\text{net}}=F_{\text{external}}-F_{\text{friction}}

(1)

Because there is no slip, $r\alpha =a$ holds. Substituting $\alpha$ and $a$ for the linear and rotational version of Newton's second law, then solving for $F_{\text{friction}}$ :

{\begin{aligned}r{\frac {\tau }{I}}&={\frac {F_{\text{net}}}{m}}\\r{\frac {rF_{\text{friction}}}{I}}&={\frac {F_{\text{net}}}{m}}\\F_{\text{friction}}&={\frac {IF_{\text{net}}}{mr^{2}}}\\\end{aligned}}

Expanding $F_{\text{friction}}$ in $(1)$ :

{\begin{aligned}F_{\text{net}}&=F_{\text{external}}-{\frac {IF_{\text{net}}}{mr^{2}}}\\&=F_{\text{external}}-{\frac {I}{mr^{2}}}F_{\text{net}}\\&={\frac {F_{\text{external}}}{1+{\frac {I}{mr^{2}}}}}\\\end{aligned}}

The last equality is the first formula for $F_{\text{net}}$ ; using it together with Newton's second law, then reducing, the formula for $a$ is obtained:

{\begin{aligned}a&={\frac {F_{\text{net}}}{m}}\\&={\frac {\left({\frac {F_{\text{external}}}{1+{\frac {I}{mr^{2}}}}}\right)}{m}}\\&={\frac {F_{\text{external}}}{m\left(1+{\frac {I}{mr^{2}}}\right)}}\\&={\frac {F_{\text{external}}}{m+{\frac {I}{r^{2}}}}}\\\end{aligned}}

The radius of gyration can be incorporated in the first formula for $F_{\text{net}}$ as follows:

{\begin{aligned}r_{\text{gyr.}}&={\sqrt {\frac {I}{m}}}\\r_{\text{gyr.}}^{2}&={\frac {I}{m}}\\{\frac {I}{mr^{2}}}&={\frac {\left({\frac {I}{m}}\right)}{r^{2}}}\\&={\frac {r_{\text{gyr.}}^{2}}{r^{2}}}\\&=\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}\\\end{aligned}}

Substituting the latest equality above in the first formula for $F_{\text{net}}$ the second formula for it:

F_{\text{net}}={\frac {F_{\text{external}}}{1+\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}}}

${\tfrac {I}{r^{2}}}$ имеет размерность массы, и это масса, которая будет иметь инерцию вращения. $I$ на расстоянии $r$ от оси вращения. Следовательно, термин ${\tfrac {I}{r^{2}}}$ можно рассматривать как массу с линейной инерцией, эквивалентной инерции вращения катящегося объекта (вокруг его центра масс). Действие внешней силы на объект при простом вращении можно представить как ускорение суммы реальной массы и виртуальной массы, которая представляет собой инерцию вращения, которая $m+{\tfrac {I}{r^{2}}}$ . Поскольку работа, совершаемая внешней силой, распределяется между преодолением поступательной и вращательной инерции, внешняя сила приводит к меньшей чистой силе за счет безразмерного мультипликативного коэффициента. $1/\left(1+{\tfrac {I}{mr^{2}}}\right)$ где ${\tfrac {I}{mr^{2}}}$ представляет собой отношение указанной виртуальной массы к фактической массе объекта и равно $\left({\tfrac {r_{\text{gyr.}}}{r}}\right)^{2}$ где $r_{\text{gyr.}}$ - это радиус вращения, соответствующий инерции вращения объекта при чистом вращении (а не инерции вращения при чистом вращении). Квадрат мощности обусловлен тем, что инерция вращения точечной массы изменяется пропорционально квадрату ее расстояния до оси.

Четыре объекта катятся по плоскости без сопротивления воздуха. Сзади вперед: сферическая оболочка (красный), сплошная сфера (оранжевый), цилиндрическое кольцо (зеленый) и сплошной цилиндр (синий). Время достижения финишной линии полностью зависит от распределения массы объекта, наклона и ускорения свободного падения. смотрите Подробности в анимированной GIF-версии .

В частном случае, когда объект катится по наклонной плоскости , испытывая только статическое трение, нормальную силу и собственный вес ( сопротивление воздуха отсутствует), ускорение в направлении скатывания вниз по склону равно:

a={\frac {g\sin \left(\theta \right)}{1+\left({\tfrac {r_{\text{gyr.}}}{r}}\right)^{2}}}

Вывод Assuming that the object is placed so as to roll downward in the direction of the inclined plane (and not partially sideways), the weight can be decomposed in a component in the direction of rolling and a component perpendicular to the inclined plane. Only the first force component makes the object roll, the second is balanced by the contact force, but it does not form an action‐reaction pair with it (just as an object in rest on a table). Therefore, for this analysis, only the first component is considered, thus: $F_{\text{external}}=gm\sin \left(\theta \right)$ ${\begin{aligned}a&={\frac {F_{\text{net}}}{m}}\\&={\frac {\left({\frac {F_{\text{external}}}{1+\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}}}\right)}{m}}\\&={\frac {\left({\frac {gm\sin \left(\theta \right)}{1+\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}}}\right)}{m}}\\&={\frac {gm\sin \left(\theta \right)}{m\left(1+\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}\right)}}\\&={\frac {g\sin \left(\theta \right)}{1+\left({\frac {r_{\text{gyr.}}}{r}}\right)^{2}}}\\\end{aligned}}$ In the last equality the denominator is the same as in the formula for force, but the factor $m$ disappears because its instance in the force of gravity cancels with its instance due to Newton's third law.

${\tfrac {r_{\text{gyr.}}}{r}}$ специфичен для формы объекта и распределения массы, он не зависит от масштаба или плотности. Однако оно будет другим, если объект будет катиться с разными радиусами; например, оно варьируется между колесной парой поезда, катящейся нормально (по шине), и по его оси. Отсюда следует, что при заданном катящемся объекте другой объект, больший по размеру или с другой плотностью, будет катиться с тем же ускорением. Это поведение такое же, как у объекта, находящегося в свободном падении, или объекта, скользящего без трения (вместо скатывания) по наклонной плоскости.

Деформируемые тела

осесимметричного деформируемого тела При контакте с поверхностью образуется интерфейс , через который могут передаваться нормальные и поперечные силы. Например, шина, контактирующая с дорогой, несет на себе вес (нормальную нагрузку) автомобиля, а также любые поперечные силы, возникающие при ускорении, торможении или рулевом управлении. Деформации и движения в устойчиво катящемся теле можно эффективно охарактеризовать, используя эйлерово описание вращения твердого тела и лагранжево описание деформации. ^{[ 2 ]}^{[ 3 ]} Этот подход значительно упрощает анализ, устраняя зависимость от времени, в результате чего поля смещения, скорости, напряжения и деформации изменяются только пространственно. Процедуры анализа методом конечных элементов для устойчивого состояния качения были впервые разработаны Падованом и в настоящее время включены в несколько коммерческих программ.

Ссылки

^ Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (13 августа 2013 г.). Основы физики, Глава 9 (10-е изд.). Уайли. ISBN 9781118230718 . Проверено 13 января 2024 г.
^ Падован, Дж.; Зейд, И. (1980). «Конечно-элементное моделирование контакта качения» . Компьютеры и конструкции . 12 (1): 77–83. дои : 10.1016/0045-7949(80)90095-4 . Проверено 28 декабря 2022 г.
^ Ци, Дж.; Херрон, младший; Сансалоне, Кхен; Марс, Западная Вирджиния; Ду, ЗЗ; Снайман, М.; Сурендранат, Х. (2007). «Подтверждение анализа установившегося транспорта для катящихся шин с протектором» . Шинная наука и технология . 35 (3): 183–208. дои : 10.2346/1.2768974 . Проверено 28 декабря 2022 г.

См. также

[1] Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (13 августа 2013 г.). Основы физики, Глава 9 (10-е изд.). Уайли. ISBN 9781118230718 . Проверено 13 января 2024 г.

[2] Падован, Дж.; Зейд, И. (1980). «Конечно-элементное моделирование контакта качения» . Компьютеры и конструкции . 12 (1): 77–83. дои : 10.1016/0045-7949(80)90095-4 . Проверено 28 декабря 2022 г.

[3] Ци, Дж.; Херрон, младший; Сансалоне, Кхен; Марс, Западная Вирджиния; Ду, ЗЗ; Снайман, М.; Сурендранат, Х. (2007). «Подтверждение анализа установившегося транспорта для катящихся шин с протектором» . Шинная наука и технология . 35 (3): 183–208. дои : 10.2346/1.2768974 . Проверено 28 декабря 2022 г.

[ 1 ]

[ 2 ]

[ 3 ]