Цепной комплекс

В математике цепной комплекс — это алгебраическая структура , состоящая из последовательности абелевых групп (или модулей ) и последовательности гомоморфизмов между последовательными группами, таких, что образ каждого гомоморфизма входит в ядро следующего. С цепным комплексом связана его гомология , которая описывает, как изображения включаются в ядра.

Коцепной комплекс подобен цепному комплексу, за исключением того, что его гомоморфизмы направлены в противоположном направлении. Гомологии коцепного комплекса называются его когомологиями .

В алгебраической топологии сингулярный цепной комплекс топологического пространства X строится с использованием непрерывных отображений симплекса в X, а гомоморфизмы цепного комплекса отражают то , как эти отображения ограничиваются границей симплекса. Гомологии этого цепного комплекса называются сингулярными гомологиями X и являются обычно используемым инвариантом топологического пространства.

Цепные комплексы изучаются в гомологической алгебре , но используются в нескольких областях математики, включая абстрактную алгебру , теорию Галуа , дифференциальную геометрию и алгебраическую геометрию . В более общем смысле их можно определить в абелевых категориях .

Определения [ править ]

Цепной комплекс $(A_{\bullet },d_{\bullet })$ представляет собой последовательность абелевых групп или модулей ..., A ₀ , A ₁ , A ₂ , A ₃ , A ₄ , ... соединенных гомоморфизмами (называемыми граничными операторами или дифференциалами ) d _n : A _n → A _{n −1} , такой, что композиция любых двух последовательных карт является нулевой картой. Явно, дифференциалы удовлетворяют условию d _n ∘ d _{n +1} = 0 или с подавленными индексами d ²= 0 . Комплекс можно записать следующим образом.

\cdots {\xleftarrow {d_{0}}}A_{0}{\xleftarrow {d_{1}}}A_{1}{\xleftarrow {d_{2}}}A_{2}{\xleftarrow {d_{3}}}A_{3}{\xleftarrow {d_{4}}}A_{4}{\xleftarrow {d_{5}}}\cdots

Коцепной комплекс $(A^{\bullet },d^{\bullet })$ – это двойственное понятие цепному комплексу. Он состоит из последовательности абелевых групп или модулей ..., A ⁰, А ¹, А ², А ³, А ⁴, ... связанные гомоморфизмами d ^н : А ^н → А ^{п +1} удовлетворение д ^{п +1} ∘ д ^н= 0 . Коцепной комплекс может быть записан аналогично цепному комплексу.

\cdots {\xrightarrow {d^{-1}}}A^{0}{\xrightarrow {d^{0}}}A^{1}{\xrightarrow {d^{1}}}A^{2}{\xrightarrow {d^{2}}}A^{3}{\xrightarrow {d^{3}}}A^{4}{\xrightarrow {d^{4}}}\cdots

Индекс n либо в An _, либо в A ^нназывается степенью (или размерностью ). Разница между цепными и коцепными комплексами заключается в том, что в цепных комплексах дифференциалы уменьшают размерность, тогда как в коцепных комплексах они увеличивают размерность. Все концепции и определения цепных комплексов применимы к коцепным комплексам, за исключением того, что они следуют другому соглашению о размерности, и часто терминам будет присвоен префикс co- . В данной статье будут даны определения цепным комплексам, когда различие не требуется.

— Ограниченный цепной комплекс в котором почти все равны это комплекс , _An 0; то есть конечный комплекс, расширенный влево и вправо на 0. Примером является цепной комплекс, определяющий симплициальные гомологии конечного симплициального комплекса . Цепной комплекс ограничен сверху, если все модули выше некоторой фиксированной степени N равны 0, и ограничен снизу, если все модули ниже некоторой фиксированной степени равны 0. Ясно, что комплекс ограничен как сверху, так и снизу тогда и только тогда, когда комплекс ограничен.

Элементы отдельных групп (ко)цепного комплекса называются (ко)цепями . Элементы ядра d называются (ко)циклами (или замкнутыми элементами), а элементы образа d называются (ко)границами (или точными элементами). Прямо из определения дифференциала все границы являются циклами. n -я группа (ко)гомологий H _n ( H ^н) — группа (ко)циклов по модулю (ко)границ степени n , т. е.

H_{n}=\ker d_{n}/{\mbox{im }}d_{n+1}\quad \left(H^{n}=\ker d^{n}/{\mbox{im }}d^{n-1}\right)

Точные последовательности [ править ]

Точная последовательность (или точный комплекс) — это цепной комплекс, все группы гомологии которого равны нулю. Это означает, что все замкнутые элементы комплекса точны. Короткая точная последовательность в которой только группы Ak _{— это ограниченная точная последовательность ,} , Ak _{+ 1} , Ak _{+ 2} могут быть ненулевыми. Например, следующий цепной комплекс представляет собой короткую точную последовательность.

\cdots {\xrightarrow {}}\;0\;{\xrightarrow {}}\;\mathbf {Z} \;{\xrightarrow {\times p}}\;\mathbf {Z} \twoheadrightarrow \mathbf {Z} /p\mathbf {Z} \;{\xrightarrow {}}\;0\;{\xrightarrow {}}\cdots

В средней группе замкнутыми элементами являются элементы p Z ; это явно точные элементы этой группы.

Карты цепочек [ править ]

Цепное отображение f между двумя цепными комплексами $(A_{\bullet },d_{A,\bullet })$ и $(B_{\bullet },d_{B,\bullet })$ это последовательность $f_{\bullet }$ гомоморфизмов $f_{n}:A_{n}\rightarrow B_{n}$ для каждого n , коммутирующего с граничными операторами на двух цепных комплексах, поэтому $d_{B,n}\circ f_{n}=f_{n-1}\circ d_{A,n}$ . Это записано в следующей коммутативной диаграмме .

Цепная карта переводит циклы в циклы, а границы в границы и, таким образом, порождает карту гомологии. $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ .

Непрерывное отображение f между топологическими пространствами X и Y индуцирует цепное отображение между сингулярными цепными комплексами X и Y отображение f _* между сингулярными гомологиями X и Y. и, следовательно, индуцирует также Когда X и Y оба равны n -сфере , отображение, индуцированное гомологиями, определяет степень отображения f .

Понятие цепной карты сводится к понятию границы посредством построения конуса цепной карты.

Цепная гомотопия [ править ]

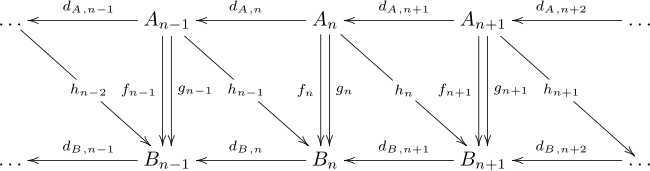
Цепная гомотопия предлагает способ связать две цепные карты, которые индуцируют одно и то же отображение в группах гомологии, даже если эти карты могут быть разными. Учитывая два цепных комплекса A и B и два цепных отображения f , g : A → B , гомотопия цепи — это последовательность гомоморфизмов h _n : A _n → B _{n +1} таких, что hd _A + d _B h = f − g . Отображения можно записать в виде следующей диаграммы, но эта диаграмма не является коммутативной.

Отображение hd _A + d _B h, как легко проверить, индуцирует нулевое отображение гомологии для любого h . Отсюда сразу следует, что f и g индуцируют одно и то же отображение гомологии. Говорят, что f и g гомотопны по цепочке (или просто гомотопны ), и это свойство определяет отношение эквивалентности между отображениями цепочек.

Пусть X и Y — топологические пространства. В случае сингулярных гомологий гомотопия между непрерывными отображениями f , g : X → Y индуцирует цепную гомотопию между цепными отображениями, соответствующими f и g . Это показывает, что два гомотопических отображения индуцируют одно и то же отображение сингулярных гомологий. Название «цепная гомотопия» мотивировано этим примером.

Примеры [ править ]

Сингулярные гомологии [ править ]

Пусть X — топологическое пространство. Определим C _n ( X ) для натурального n как свободную абелеву группу, формально порожденную сингулярными n-симплексами в X , и определим граничное отображение $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ быть

\partial _{n}:\,(\sigma :[v_{0},\ldots ,v_{n}]\to X)\mapsto (\sum _{i=0}^{n}(-1)^{i}\sigma :[v_{0},\ldots ,{\hat {v}}_{i},\ldots ,v_{n}]\to X)

где шляпка обозначает пропуск вершины . То есть граница сингулярного симплекса представляет собой знакопеременную сумму ограничений на его грани. Можно показать, что ∂ ² = 0, поэтому $(C_{\bullet },\partial _{\bullet })$ представляет собой цепной комплекс; сингулярная гомология $H_{\bullet }(X)$ является гомологией этого комплекса.

Сингулярные гомологии — полезный инвариант топологических пространств с точностью до гомотопической эквивалентности . Группа гомологии нулевой степени является свободной абелевой группой на пути X . компонентах

когомологии де Рама [ править ]

Дифференциальные , k -формы на любом гладком многообразии M образуют вещественное векторное пространство называемое Ω ^к( М ) в дополнении. Внешняя производная d отображает Ω ^к( M ) к Ω ^{к +1}( М ) и d ² = 0 по существу следует из симметрии вторых производных , поэтому векторные пространства k -форм вместе с внешней производной представляют собой коцепной комплекс.

0{\stackrel {\subset }{\to }}\ {\Re ^{c}}{\stackrel {\subset }{\to }}\ {\Omega ^{0}(M)}{\stackrel {d}{\to }}\ {\Omega ^{1}(M)}{\stackrel {d}{\to }}\ {\Omega ^{2}(M)}{\stackrel {d}{\to }}\ \Omega ^{3}(M)\to \cdots

Когомологии этого комплекса называются де Рама когомологиями М . Локально постоянные функции обозначаются своим изоморфизмом $\Re ^{c}$ где c — количество взаимно несвязных M. компонентов Таким образом, комплекс был расширен, чтобы оставить комплекс точным на уровне нулевой формы с использованием оператора подмножества.

Гладкие отображения между многообразиями индуцируют цепные отображения, а гладкие гомотопии между отображениями индуцируют цепные гомотопии.

Категория цепных комплексов [ править ]

Цепные комплексы K -модулей с цепными отображениями образуют категорию Ch _K , где K — коммутативное кольцо.

Если В = В ${}_{*}$ и W = W ${}_{*}$ являются цепными комплексами, их тензорное произведение $V\otimes W$ представляет собой цепной комплекс с элементами степени n , заданными формулой

(V\otimes W)_{n}=\bigoplus _{\{i,j|i+j=n\}}V_{i}\otimes W_{j}

и дифференциал, заданный формулой

\partial (a\otimes b)=\partial a\otimes b+(-1)^{\left|a\right|}a\otimes \partial b

где a и b — любые два однородных вектора в V и W соответственно, и $\left|a\right|$ обозначает степень a .

Это тензорное произведение превращает категорию Ch _K в симметричную моноидальную категорию . Объектом идентичности относительно этого моноидального произведения является базовое кольцо K , рассматриваемое как цепной комплекс степени 0. Расплетение задается на простых тензорах однородных элементов формулой

a\otimes b\mapsto (-1)^{\left|a\right|\left|b\right|}b\otimes a

Признак необходим для того, чтобы плетение представляло собой карту цепочки.

Более того, категория цепных комплексов K -модулей также имеет внутренний Hom : для данных цепных комплексов V и W внутренний Hom V и W , обозначаемый Hom( V , W ), представляет собой цепной комплекс с элементами степени n , заданный формулой $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ и дифференциал, заданный формулой