Оптимизация роя частиц

Рой частиц ищет глобальный минимум функции

В вычислительной науке оптимизация роя частиц ( PSO ) — это вычислительный метод, который оптимизирует задачу, итеративно пытаясь улучшить возможное решение с учетом заданной меры качества. Он решает проблему, имея совокупность возможных решений, называемых здесь частицами , и перемещая эти частицы в пространстве поиска в соответствии с простыми математическими формулами частицы относительно положения и скорости . На движение каждой частицы влияет ее локальное наиболее известное положение, но оно также направляется к наиболее известным позициям в пространстве поиска, которые обновляются по мере того, как другие частицы находят лучшие позиции. Ожидается, что это подтолкнет рой к лучшим решениям.

PSO первоначально приписывается Кеннеди , Эберхарту и Ши. и изначально предназначался для моделирования социального поведения , как стилизованное изображение движения организмов в птичьей стае или косяке рыб . Алгоритм был упрощен, и было замечено, что он выполняет оптимизацию. Книга Кеннеди и Эберхарта описывает многие философские аспекты PSO и роевого интеллекта . Обширный обзор приложений PSO проведен Poli . В 2017 году Боньяди и Михалевич опубликовали всеобъемлющий обзор теоретических и экспериментальных работ по PSO.

PSO является метаэвристическим подходом , поскольку он делает мало или вообще не делает предположений относительно оптимизируемой проблемы и может искать в очень больших пространствах возможных решений. Кроме того, PSO не использует градиент оптимизируемой задачи, а это означает, что PSO не требует, чтобы задача оптимизации была дифференцируемой , как того требуют классические методы оптимизации, такие как градиентный спуск и методы квазиньютонов . Однако метаэвристика, такая как PSO, не гарантирует, что оптимальное решение когда-либо будет найдено.

Алгоритм

Базовый вариант алгоритма PSO работает за счет наличия популяции (называемой рой) решений-кандидатов (называемых частицами). Эти частицы перемещаются в пространстве поиска в соответствии с несколькими простыми формулами. Движения частиц управляются их собственным наиболее известным положением в пространстве поиска, а также наиболее известным положением всего роя. Когда будут обнаружены улучшенные позиции, они начнут направлять движения роя. Процесс повторяется, и при этом есть надежда, но не гарантия, что в конечном итоге будет найдено удовлетворительное решение.

Формально, пусть f : ℝ ^н → ℝ — функция стоимости, которую необходимо минимизировать. Функция принимает решение-кандидат в качестве аргумента в форме вектора действительных чисел и выдает на выходе вещественное число, которое указывает значение целевой функции данного решения-кандидата. Градиент ​ f . неизвестен Цель состоит в том, чтобы найти решение a, для которого f ( a ) ≤ f ( b ) для всех b в пространстве поиска, что будет означать, что a является глобальным минимумом.

Пусть S — количество частиц в рое, каждая из которых имеет позицию x _i ∈ ℝ ^н в пространстве поиска и скорость v _i ∈ ℝ ^н . Пусть p _i — наилучшее известное положение частицы i , а g — наилучшее известное положение всего роя. Тогда базовый алгоритм PSO для минимизации функции стоимости:

for each particle i = 1, ..., S do
    Initialize the particle's position with a uniformly distributed random vector: xi ~ U(blo, bup)
    Initialize the particle's best known position to its initial position: pi ← xi
    if f(pi) < f(g) then
        update the swarm's best known position: g ← pi
    Initialize the particle's velocity: vi ~ U(-|bup-blo|, |bup-blo|)
while a termination criterion is not met do:
    for each particle i = 1, ..., S do
        for each dimension d = 1, ..., n do
            Pick random numbers: rp, rg ~ U(0,1)
            Update the particle's velocity: vi,d ← w vi,d + φp rp (pi,d-xi,d) + φg rg (gd-xi,d)
        Update the particle's position: xi ← xi + vi
        if f(xi) < f(pi) then
            Update the particle's best known position: pi ← xi
            if f(pi) < f(g) then
                Update the swarm's best known position: g ← pi

Значения b _lo и b _up представляют нижнюю и верхнюю границы пространства поиска соответственно. Параметр w — это инерционный вес. Параметры φ _p и φ _g часто называют когнитивным коэффициентом и социальным коэффициентом.

Критерием завершения может быть количество выполненных итераций или решение, в котором найдено адекватное значение целевой функции. Параметры w, φ _p и φ _g выбираются практикующим врачом и контролируют поведение и эффективность метода PSO ( ниже ).

Выбор параметров

Ландшафт производительности, показывающий, как простой вариант PSO работает в совокупности при решении нескольких эталонных задач при изменении двух параметров PSO.

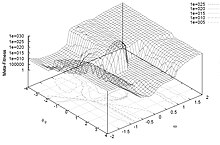
Выбор параметров PSO может оказать большое влияние на производительность оптимизации. Поэтому выбор параметров PSO, обеспечивающих хорошую производительность, стал предметом многочисленных исследований.

Чтобы предотвратить расхождение («взрыв»), вес инерции должен быть меньше 1. Два других параметра могут быть затем получены благодаря подходу сужения: или свободно выбраны, но анализ предполагает области конвергенции, ограничивающие их. Типичные значения находятся в $[1,3]$.

Параметры PSO также можно настроить с помощью другого наложенного оптимизатора — концепции, известной как метаоптимизация . или даже дорабатываться в ходе оптимизации, например, с помощью нечеткой логики.

Параметры также были настроены для различных сценариев оптимизации.

Окрестности и топологии

Топология роя определяет подмножество частиц, с которыми каждая частица может обмениваться информацией. Базовая версия алгоритма использует глобальную топологию в качестве роевой структуры связи. Эта топология позволяет всем частицам взаимодействовать со всеми другими частицами, таким образом, весь рой занимает одно и то же лучшее положение g для одной частицы. Однако такой подход может привести к тому, что рой окажется в ловушке локального минимума, таким образом, для управления потоком информации между частицами использовались разные топологии. Например, в локальных топологиях частицы обмениваются информацией только с подмножеством частиц. Это подмножество может быть геометрическим. – например « m ближайших частиц» – или, чаще, социальная, т.е. совокупность частиц, не зависящая ни от какого расстояния. В таких случаях вариант PSO считается лучшим на местном уровне (по сравнению с глобальным лучшим вариантом базового PSO).

Обычно используемая топология роя — это кольцо, в котором у каждой частицы есть только два соседа, но есть и множество других. Топология не обязательно статична. Фактически, поскольку топология связана с разнообразием сообщений частиц, были предприняты некоторые усилия по созданию адаптивных топологий (СПСО, АПСО, стохастическая звезда, ПЛЕМЕНА, Кибер Рой, и C-PSO )

Используя кольцевую топологию, PSO может достичь параллелизма на уровне поколений, что значительно увеличивает скорость эволюции.

Внутренняя работа

Существует несколько точек зрения относительно того, почему и как алгоритм PSO может выполнять оптимизацию.

Среди исследователей распространено мнение, что поведение стаи варьируется от исследовательского поведения, то есть поиска в более широкой области поискового пространства, до эксплуататорского поведения, то есть локально-ориентированного поиска с целью приблизиться к (возможно, локальному) объекту. оптимум. Эта школа мысли была распространена с момента создания PSO. Эта школа мысли утверждает, что алгоритм PSO и его параметры должны быть выбраны так, чтобы правильно балансировать между исследованием и эксплуатацией, чтобы избежать преждевременной сходимости к локальному оптимуму , но при этом обеспечить хорошую скорость сходимости к оптимуму. Это убеждение является предшественником многих вариантов PSO, см . ниже .

Другая школа мысли заключается в том, что поведение роя PSO недостаточно изучено с точки зрения того, как оно влияет на реальную производительность оптимизации, особенно для многомерных пространств поиска и задач оптимизации, которые могут быть прерывистыми, зашумленными и меняющимися во времени. Эта школа мысли просто пытается найти алгоритмы и параметры PSO, которые обеспечивают хорошую производительность независимо от того, как поведение стаи можно интерпретировать, например, в отношении разведки и эксплуатации. Подобные исследования привели к упрощению алгоритма PSO, см. ниже .

Конвергенция

В отношении PSO слово «конвергенция» обычно относится к двум различным определениям:

• Сходимость последовательности решений (также известная как анализ устойчивости, сходимость ), в которой все частицы сошлись к точке в пространстве поиска, которая может быть, а может и не быть оптимальной,
• Сходимость к локальному оптимуму, при котором все личные рекорды p или, альтернативно, наиболее известная позиция роя g приближаются к локальному оптимуму задачи, независимо от того, как ведет себя рой.

Исследована сходимость последовательности решений для ПСО. В результате этих анализов были разработаны рекомендации по выбору параметров PSO, которые, как считается, вызывают сходимость к точке и предотвращают расхождение частиц роя (частицы не движутся неограниченно и будут куда-то сходиться). Однако анализы подверглись критике со стороны Педерсена. за чрезмерное упрощение, поскольку они предполагают, что рой состоит только из одной частицы, что он не использует стохастические переменные и что точки притяжения, то есть наилучшее известное положение частицы p и наилучшее известное положение роя g , остаются постоянными на протяжении всего процесса оптимизации. . Однако было показано что эти упрощения не влияют на границы, обнаруженные в этих исследованиях для параметра, в котором рой сходится. В последние годы были предприняты значительные усилия, чтобы ослабить допущения моделирования, используемые при анализе стабильности PSO. при этом самый последний обобщенный результат был применен к многочисленным вариантам PSO и использовал, как было показано, минимально необходимые допущения моделирования.

Сходимость к локальному оптимуму была проанализирована для PSO в и. Было доказано, что PSO нуждается в некоторой модификации, чтобы гарантировать нахождение локального оптимума.

Это означает, что определение возможностей сходимости различных алгоритмов и параметров PSO по-прежнему зависит от эмпирических результатов. Одной из попыток решения этой проблемы является разработка стратегии «ортогонального обучения» для улучшения использования информации, уже существующей во взаимосвязи между p и g , чтобы сформировать ведущий сходящийся образец и быть эффективным с любой топологией PSO. Цель состоит в том, чтобы улучшить производительность PSO в целом, включая более быструю глобальную конвергенцию, более высокое качество решений и более высокую надежность. Однако такие исследования не предоставляют теоретических доказательств, подтверждающих их утверждения.

Адаптивные механизмы

Без необходимости компромисса между конвергенцией («эксплуатацией») и дивергенцией («исследованием») можно ввести адаптивный механизм. Адаптивная оптимизация роя частиц (APSO) отличается большей эффективностью поиска, чем стандартный PSO. APSO может выполнять глобальный поиск по всему пространству поиска с более высокой скоростью сходимости. Это позволяет автоматически контролировать инерционный вес, коэффициенты ускорения и другие алгоритмические параметры во время выполнения, тем самым одновременно повышая эффективность и результативность поиска. Кроме того, APSO может воздействовать на лучшую в глобальном масштабе частицу, чтобы выпрыгнуть из вероятного локального оптимума. Однако APSO представит новые параметры алгоритма, тем не менее, он не вносит дополнительной сложности в проектирование или реализацию.

Кроме того, благодаря использованию механизма оценки пригодности, адаптируемого к масштабу, PSO может эффективно решать вычислительно затратные задачи оптимизации.

Варианты

Возможны многочисленные варианты даже базового алгоритма PSO. Например, существуют разные способы инициализации частиц и скоростей (например, начать с нулевых скоростей), как уменьшить скорость, обновить значения pi и g только обновления _после всего роя и т. д. Некоторые из этих вариантов и их Возможное влияние на производительность обсуждалось в литературе.

Ведущими исследователями был создан ряд стандартных реализаций, «предназначенных для использования как в качестве основы для тестирования производительности усовершенствований метода, так и для представления PSO более широкому сообществу специалистов по оптимизации. Имея хорошо известные, строго определенные Стандартный алгоритм обеспечивает ценную точку сравнения, которую можно использовать во всех областях исследований, чтобы лучше тестировать новые достижения». Последним является Стандарт ПСО 2011 (СПСО-2011).

Гибридизация

Новые и более сложные варианты PSO также постоянно вводятся в попытке улучшить производительность оптимизации. В этих исследованиях есть определенные тенденции; один — создать гибридный метод оптимизации с использованием PSO в сочетании с другими оптимизаторами, например, комбинированное PSO с оптимизацией на основе биогеографии, и внедрение эффективного метода обучения.

Устранение преждевременной конвергенции

Другая исследовательская тенденция состоит в том, чтобы попытаться облегчить преждевременную сходимость (то есть стагнацию оптимизации), например, обращая вспять или возмущая движение частиц PSO. Еще один подход к борьбе с преждевременной конвергенцией — использование нескольких роев. ( многороевая оптимизация ). Многороевой подход также можно использовать для реализации многоцелевой оптимизации. Наконец, есть разработки по адаптации поведенческих параметров PSO во время оптимизации.

Упрощения

Другая точка зрения состоит в том, что PSO следует максимально упростить, не ухудшив при этом его эффективность; общая концепция, которую часто называют бритвой Оккама . Упрощение PSO было первоначально предложено Кеннеди. и изучается более подробно, где оказалось, что производительность оптимизации улучшилась, параметры стало легче настраивать, и они работали более стабильно при решении различных задач оптимизации.

Еще один аргумент в пользу упрощения PSO заключается в том, что эффективность метаэвристики можно продемонстрировать только эмпирически, проводя вычислительные эксперименты над конечным числом задач оптимизации. Это означает, что метаэвристика, такая как PSO, не может быть доказана корректной , и это увеличивает риск ошибок в ее описании и реализации. Хороший пример этого представил многообещающий вариант генетического алгоритма (еще одна популярная метаэвристика), но позже он оказался дефектным, поскольку при поиске оптимизации он был сильно смещен в сторону аналогичных значений для разных измерений в пространстве поиска, что оказалось оптимальным для эталона. рассмотренные проблемы. Это смещение произошло из-за ошибки программирования и теперь исправлено.

Голые кости ПСО

Инициализация скоростей может потребовать дополнительных входных данных. Вариант Bare Bones PSO был предложен в 2003 году Джеймсом Кеннеди и вообще не требует использования скорости.

В этом варианте PSO отказываются от скорости частиц и вместо этого обновляют положения частиц, используя следующее простое правило:

${\vec {x}}_{i}=G\left({\frac {{\vec {p}}_{i}+{\vec {g}}}{2}},||{\vec {p}}_{i}-{\vec {g}}||\right)\,,$

где ${\vec {x}}_{i}$, ${\vec {p}}_{i}$ - положение и наилучшее положение частицы $i$; ${\vec {g}}$ это лучшая глобальная позиция; $G({\vec {x}},\sigma )$ это нормальное распределение со средним значением ${\vec {x}}$ и стандартное отклонение $\sigma$; и где $||\dots ||$ означает норму вектора.

Ускоренная оптимизация роя частиц

Другой более простой вариант — оптимизация роя ускоренных частиц (APSO). который также не требует использования скорости и может ускорить сходимость во многих приложениях. Доступен простой демонстрационный код APSO.

В этом варианте PSO отказываются как от скорости частицы, так и от ее наилучшего положения. Положение частицы обновляется в соответствии со следующим правилом:

${\vec {x}}_{i}\leftarrow (1-\beta ){\vec {x}}_{i}+\beta {\vec {g}}+\alpha L{\vec {u}}\,,$

где ${\vec {u}}$ — случайный равномерно распределенный вектор, $L$ - типичная длина рассматриваемой проблемы, и $\beta \sim 0.1-0.7$ и $\alpha \sim 0.1-0.5$ являются параметрами метода. При усовершенствовании метода можно уменьшить $\alpha$ с каждой итерацией, $\alpha _{n}=\alpha _{0}\gamma ^{n}$, где $n$ номер итерации и $0<\gamma <1$ – параметр управления уменьшением.

Многокритериальная оптимизация

PSO также применяется для решения многоцелевых задач . в котором сравнение целевой функции учитывает доминирование Парето при движении частиц PSO, а недоминированные решения сохраняются так, чтобы аппроксимировать фронт Парето.

Бинарный, дискретный и комбинаторный

Поскольку приведенные выше уравнения PSO работают с действительными числами, обычно используемый метод решения дискретных задач состоит в отображении дискретного пространства поиска в непрерывную область, применении классического PSO, а затем обратном отображении результата. Такое сопоставление может быть очень простым (например, с использованием округленных значений) или более сложным.

Однако можно отметить, что в уравнениях движения используются операторы, выполняющие четыре действия:

• вычисление разницы двух позиций. Результатом является скорость (точнее перемещение)
• умножение скорости на числовой коэффициент
• сложение двух скоростей
• применение скорости к позиции

Обычно положение и скорость представляются n действительными числами, и эти операторы — это просто -, *, + и снова +. Но все эти математические объекты можно определить совершенно по-другому, чтобы справиться с бинарными задачами (или, в более общем случае, дискретными) или даже комбинаторными задачами. Один из подходов — переопределить операторы на основе множеств.

См. также

• Алгоритм искусственной пчелиной семьи
• Алгоритм пчел
• Оптимизация без производных
• Многороевая оптимизация
• Фильтр твердых частиц
• Роевой интеллект
• Поиск косяка рыбы
• Дисперсионная оптимизация мух

Внешние ссылки

• Particle Swarm Central — это хранилище информации о PSO. Несколько исходных кодов находятся в свободном доступе.
• Краткое видео о том, как рои частиц оптимизируют три функции тестирования.
• Моделирование сходимости PSO в двумерном пространстве (Matlab).
• Приложения ПСО.
• Лю, Ян (2009). «Автоматическая калибровка модели осадков и стока с использованием быстрого и элитарного многокритериального алгоритма роя частиц». Экспертные системы с приложениями . 36 (5): 9533–9538. дои : 10.1016/j.eswa.2008.10.086 .
• Ссылки на исходный код PSO