Как не ошибиться
 Издание в твердом переплете | |
| Автор | Джордан Элленберг |
|---|---|
| Язык | Английский |
| Жанр | Математика |
| Издатель | Пингвин Групп |
Дата публикации | 29 мая 2014 г. |
| Место публикации | Соединенные Штаты |
| Тип носителя | Распечатать |
| Страницы | 468 стр. |
| ISBN | 978-1594205224 |
Книга «Как не ошибиться: сила математического мышления» , написанная Джорданом Элленбергом , стала бестселлером по версии New York Times. [1] книга, которая соединяет различные экономические и социальные философии с основами математики и статистическими принципами. [2] [3]
Краткое содержание
[ редактировать ]Книга « Как не ошибаться» объясняет математические принципы, лежащие в основе некоторых простейших повседневных мыслей. [4] Затем это переходит в более сложные решения, которые принимают люди. [5] [6] Например, Элленберг объясняет многие неправильные представления о лотереях и о том, можно ли их обыграть математически. [7] [8]
Элленберг использует математику для изучения проблем реального мира, начиная от любви к прямым линиям в отчетах об ожирении и заканчивая теорией игр о пропущенных рейсах, от значимости регрессии до среднего значения и парадокса Берксона , который противоречит здравому смыслу . [7] [9]
Краткое содержание глав
[ редактировать ]Часть 1: Линейность
[ редактировать ]Глава 1, «Менее похоже на Швецию»: Элленберг призывает своих читателей мыслить нелинейно и знать, что «куда вам следует идти, зависит от того, где вы находитесь». Чтобы развить свою мысль, он связывает это с экономикой Вуду и Лаффера кривой налогообложения . Хотя в этой главе мало цифр, суть в том, что общая концепция по-прежнему связана с математическим мышлением. [10]
Глава 2, Прямая локально, изогнутая глобально. В этой главе особое внимание уделяется признанию того, что «не каждая кривая является прямой линией», и упоминаются многочисленные математические концепции, включая теорему Пифагора, вывод числа Пи, парадокс Зенона и не- стандартный анализ . [10]
Глава 3 «Все страдают ожирением». Здесь Элленберг анализирует некоторые общие статистические данные о тенденциях ожирения в Соединенных Штатах. Он связывает это с линейной регрессией и указывает на основные противоречия, содержащиеся в первоначальных представленных аргументах. Чтобы доказать свою точку зрения, он использует множество примеров, в том числе корреляцию между баллами SAT и оплатой за обучение, а также траекторией ракет. [10]
Глава 4, Сколько это погибших американцев: Элленберг анализирует статистику о количестве жертв по всему миру в разных странах в результате войны. Он отмечает, что, хотя пропорция в этих случаях имеет значение, она не всегда имеет смысл, если связывать их со смертями американцев. Чтобы подкрепить свою точку зрения , он использует примеры смертей из-за рака мозга, биномиальную теорему и опросы общественного мнения. [10]
Глава 5, «Больше пирога, чем тарелки». В этой главе подробно рассматриваются процентные соотношения, связанные с уровнем занятости, и упоминаются политические обвинения. Он подчеркивает, что «в этих случаях важны не реальные цифры, а знание того, на что делить, что и есть математика в ее истинном виде», отмечая, что математика сама по себе есть во всем. [10]
Часть 2: Вывод
[ редактировать ]Глава 6, «Балтиморский биржевой маклер и библейский код»: Элленберг пытается донести, что математика присутствует во всем, что мы делаем. Чтобы подтвердить это, он использует примеры скрытых кодов в Торе, определяемых Равноотстоящей Последовательностью Букв , притчу о биржевом маклере, отмечая, что «происходят невероятные вещи», и приписывает этому пространство для маневра. [11]
Глава 7. Мертвая рыба. Не читайте мысли. В этой главе затрагивается множество вещей. В основу этой главы легли истории о МРТ мертвого лосося, методе проб и ошибок в алгебре, статистике противозачаточных средств, а также баскетбольной статистике (« горячая рука »). Он также отмечает, что поэзию можно сравнить с математикой в том смысле, что она «тренируется под воздействием стимулов и ею можно манипулировать в лаборатории». Кроме того, он пишет о нескольких других математических концепциях, включая нулевую гипотезу и функцию четвертой степени . [11]
Глава 8, Reductio Ad вряд ли: Эта глава посвящена работам и теоремам/концепциям многих известных математиков и философов. К ним относятся, помимо прочего, « Reductio Ad Absurdum» , Аристотеля взгляд на созвездие Тельца Джона Митчелла и гипотеза Итана «Тома» Чжана об «ограниченных пробелах». Он также углубляется в объяснение рациональных чисел, теоремы о простых числах и придумал собственное слово «флогарифмы». [11]
Глава 9, Международный журнал гаруспичности: Элленберг связывает практику гаруспичности , гены, влияющие на шизофрению, точность опубликованных статей, а также другие вещи со «значением P» или статистической значимостью. В конце он также отмечает, что Ежи Нейман и Эгон Пирсон утверждали, что статистика — это действие, а не интерпретация, а затем соотносит это с другими примерами из реальной жизни. [11]
Глава 10: Ты здесь, Боже? Это я, байесовский вывод . В этой главе алгоритмы связаны с самыми разными вещами: от Бога до рекомендаций фильмов Netflix и терроризма на Facebook . В этой главе Элленберг рассматривает довольно много математических концепций, в том числе условные вероятности, относящиеся к «значению P», апостериорные возможности, байесовский вывод и теорему Байеса , поскольку они коррелируют с радиопсихическими явлениями и вероятностью. Кроме того, он использует квадраты Пеннета и другие методы для исследования вероятности существования Бога. [11]
Часть 3: Ожидание
[ редактировать ]Глава 11. Чего ожидать, когда вы рассчитываете выиграть в лотерею. В этой главе обсуждаются различные вероятности выигрыша в лотерею и ожидаемая стоимость применительно к лотерейным билетам, включая историю о том, как студентам Массачусетского технологического института удалось «выиграть» в лотерею. каждый раз в своем городе. Элленберг также снова говорит о Законе больших чисел, а также вводит аддитивность ожидаемого значения и игры Франка-Карро или « проблему иглы / лапши ». В этой главе упоминаются многие математики и другие известные люди, в том числе Жорж-Луи Леклер, граф де Бюффон и Джеймс Гарви. [12]
Глава 12, Мисс больше самолетов. Математические понятия в этой главе включают в себя полезность и utils , а также кривую Лаффера. В этой главе обсуждается количество времени, проведенное в аэропорту, в связи с опозданием на рейс, Даниэлем Эллсбергом , мыслями Блеза Паскаля, еще раз о вероятности Бога и петербургским парадоксом . [12]
Глава 13, «Там, где встречаются железнодорожные пути». В этой главе снова обсуждаются лотерея и геометрия в картинах эпохи Возрождения. В нем представлены некоторые сведения о кодировании, в том числе код исправления ошибок, код Хэмминга и кодовые слова. Он также упоминает расстояние Хэмминга применительно к языку. Математические понятия, включенные в эту главу, — это дисперсия , проективная плоскость , плоскость Фано и гранецентрированная кубическая решетка. [12]
Часть 4: Регрессия
[ редактировать ]Глава 14, «Триумф посредственности». В этой главе обсуждается посредственность в повседневном бизнесе, согласно Горацию Секристу . Он также включает дискуссии о Фрэнсиса Гальтона и бейсбольную статистику хоум-ранов. «Наследственном гении» [13]
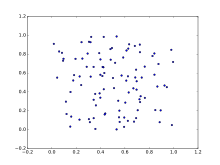
Глава 15, Эллипс Гальтона: Эта глава посвящена сэру Фрэнсису Гальтону и его работе над диаграммами рассеяния , а также эллипсами, образованными ими, корреляцией и причинно-следственной связью, а также развитием от линейных систем к квадратичным. В этой главе также рассматриваются условное и безусловное математическое ожидание, регрессия к среднему значению , эксцентриситет , двумерное нормальное распределение и размеры в геометрии. [13]
Глава 16. Заставляет ли рак легких курить сигареты. В этой главе исследуется взаимосвязь между курением сигарет и раком легких с использованием работы Р. А. Фишера. Это также касается заблуждения Берксона и использует привлекательность мужчин для развития мысли, а в конце говорит об общем эффекте. [13]
Часть 5: Существование
[ редактировать ]Глава 17, «Общественное мнение не существует». Эта глава углубляется в работу системы правил большинства и указывает на противоречия и путаницу во всем этом, в конечном итоге заявляя, что общественного мнения не существует. Чтобы доказать свою точку зрения, он использует множество примеров, в том числе различную статистику выборов, смертный приговор умственно отсталому человеку и дело с судьей Антонином Скалиа . Он также включает математические термины/концепции, такие как независимость нерелевантных альтернатив , эффект асимметричного доминирования Австралии , единый передаваемый голос и парадоксы Кондорсе . [14]
Глава 18, «Из ничего я создал странную новую вселенную»: В этой главе рассказывается о Яноше Больайсе и его работе над постулатом параллельности. В этой главе упоминаются также Давид Гильберт и Готтлоб Фреге . Он также исследовал точки и линии, формализм и то, что автор называет «гениальным» менталитетом. [14]
Как быть правым
[ редактировать ]В этой последней главе представлена последняя концепция, ex falso quodlibet , и упоминается Теодор Рузвельт , а также выборы между Обамой и Ромни . Автор завершает книгу обнадеживающими заявлениями, отмечая, что не знать всего — это нормально и что мы все учимся на неудачах. В конце он говорит, что любить математику — значит быть «тронутым огнем и связанным разумом», и что мы все должны хорошо ею пользоваться. [15]
Прием
[ редактировать ]Билл Гейтс одобрил книгу «Как не ошибаться» и включил ее в свой список «5 книг, которые стоит прочитать этим летом» 2016 года. [16] [17]
Газета Washington Post сообщила, что книга «блестяще увлекательна... часть чистой интеллектуальной радости от книги заключается в том, что автор ловко перескакивает с темы на тему, сравнивая слизевиков. [18] к голосованию Буша-Гора во Флориде, криминология к Девятой симфонии Бетховена. Конечный результат представляет собой одну огромную мозаику, объединенную математикой». [19]
Газета Wall Street Journal сообщила: «Пиши Элленберга представляют собой своего рода рентгеновские снимки, которые раскрывают скрытые структуры под беспорядочной и хаотичной поверхностью мира». [20] The Guardian писала: «Проза Элленберга вызывает восхищение: неформальная и яркая, непочтительная, но серьезная». [21]
Бизнес-инсайдер сказал, что это «Сборник увлекательных примеров математики и ее удивительных приложений… Как не ошибиться, полный интересных и странных математических инструментов и наблюдений». [22]
Еженедельник Publishers пишет: «Жирно, доступно и занимательно... Элленберг обнаруживает, что здравый смысл математики работает в повседневном мире, а его яркие примеры и ясные описания показывают, как «математика вплетена в то, как мы рассуждаем»». [23]
Times Higher Education отмечает: « Как не ошибаться» прекрасно написано, удерживает внимание читателя на протяжении всего времени благодаря хорошо подобранному материалу, яркому изложению, остроумию и полезным примерам... Элленберг разделяет замечательную способность Гарднера писать ясно и увлекательно, привнося глубокие знания. математические идеи без того, чтобы читатель заметил их трудность». [24]
Салон описывает книгу так: «Поэт-математик предлагает вдохновляющее и интересное пособие по эпохе больших данных... Полезная популярная книга по математике практически для всех». [25]
Ссылки
[ редактировать ]- ^ «Художественные книги в твердом переплете — бестселлеры — 22 июня 2014 г. — The New York Times» . Нью-Йорк Таймс . Проверено 25 апреля 2018 г.
- ^ Крейс, Джон (8 июня 2014 г.). «Как не ошибиться: скрытая математика повседневной жизни Джордана Элленберга – прочтение в переваренном виде» . Хранитель .
- ^ «Обзор книги Джордана Элленберга «Как не ошибаться: сила математического мышления» - The Boston Globe» . Бостон Глобус .
- ^ Таймс, Лос-Анджелес (18 июня 2014 г.). «В книге «Как не ошибаться» Джордан Элленберг придает математике смысл» . Лос-Анджелес Таймс .
- ^ Бёрд, Орландо (13 июня 2014 г.). « Как не ошибиться: скрытая математика повседневной жизни», Джордан Элленберг» . Файнэншл Таймс . ISSN 0307-1766 .
- ^ Элленберг, Джордан (13 июня 2014 г.). «Как я ошибался» . Сланец . ISSN 1091-2339 .
- ^ Перейти обратно: а б «Мыслить внутри коробки | О Висконсине» . В Висконсине .
- ^ «Как разбогатеть, играя в лотерею | Математическая ассоциация Америки» . www.maa.org .
- ^ «Математик объясняет, как определить, во сколько добраться до аэропорта перед вылетом» . Бизнес-инсайдер .
- ^ Перейти обратно: а б с д и Элленберг, Джордан (2014). Как не ошибиться: сила математического мышления . Книги о пингвинах. стр. 21–85 . ISBN 978-0-14-312753-6 .
- ^ Перейти обратно: а б с д и Элленберг, Джордан (2014). Как не ошибиться: сила математического мышления . Книги о пингвинах. стр. 89 –191.
- ^ Перейти обратно: а б с Элленберг, Джордан (2014). Как не ошибиться: сила математического мышления . Книги о пингвинах. стр. 196–291 .
- ^ Перейти обратно: а б с Элленберг, Джордан (2014). Как не ошибиться: сила математического мышления . Книги о пингвинах. стр. 295–362 .
- ^ Перейти обратно: а б Элленберг, Джордан (2014). Как не ошибиться: сила математического мышления . Книги о пингвинах. стр. 365–420 .
- ^ Элленберг, Джордан (2014). Как не ошибиться: сила математического мышления . Книги о пингвинах. стр. 421–437 .
- ^ Гейтс, Билл. «Как математика тайно влияет на вашу жизнь» . www.gatesnotes.com .
- ^ Гейтс, Билл. «5 книг, которые стоит прочитать этим летом» . www.gatesnotes.com .
- ^ Джабр, Феррис (7 ноября 2012 г.). «Как безмозглые слизевики меняют определение интеллекта» . www.scientificamerican.com . Научный американец .
- ^ Сури, Манил (13 июня 2014 г.). Рецензия на книгу Джордана Элленберга «Как не ошибаться: сила математического мышления» . Вашингтон Пост . ISSN 0190-8286 .
- ^ Ливио, Марио (13 июня 2014 г.). «Рецензия на книгу Джордана Элленберга: «Как не ошибиться»» . Уолл Стрит Джорнал . ISSN 0099-9660 .
- ^ Беллос, Алекс (13 июня 2014 г.). «Как не ошибиться: Скрытая математика повседневной жизни Джордана Элленберга – обзор» . Хранитель .
- ^ «Математик объясняет, как определить, во сколько добраться до аэропорта перед вылетом» . Бизнес-инсайдер . Проверено 23 апреля 2018 г.
- ^ «Рецензия на научно-популярную книгу: Как не ошибаться: сила математического мышления Джордана Элленберга. Penguin Press, 27,95 долларов США (480p) ISBN 978-1-59420-522-4» . ИздательствоWeekly.com . Проверено 23 апреля 2018 г.
- ^ «Как не ошибиться: скрытая математика повседневной жизни», Джордан Элленберг . Высшее образование Times (THE) . 05.06.2014 . Проверено 23 апреля 2018 г.
- ^ « Как не ошибаться»: чему литературный мир может научиться у математики» . Салон . 08.06.2014 . Проверено 23 апреля 2018 г.