Модель Барабаши – Альберта

Отображение трех графиков, созданных с помощью модели Барабаси-Альберта (BA). Каждый имеет 20 узлов и указанный параметр присоединения m. Цвет каждого узла зависит от его степени (одинаковый масштаб для каждого графика).

Модель Барабаши-Альберта (BA) представляет собой алгоритм создания случайных безмасштабных сетей с использованием механизма предпочтительного прикрепления . Некоторые естественные и созданные человеком системы, включая Интернет , Всемирную паутину , сети цитирования и некоторые социальные сети, считаются примерно безмасштабными и, безусловно, содержат несколько узлов (называемых концентраторами) с необычно высокой степенью по сравнению с другими. узлы сети. Модель BA пытается объяснить существование таких узлов в реальных сетях. Алгоритм назван в честь его изобретателей Альберта-Ласло Барабаши и Реки Альберта .

Концепции

Многие наблюдаемые сети (по крайней мере приблизительно) попадают в класс безмасштабных сетей , что означает, что они имеют степенное (или безмасштабное) распределение степеней, в то время как модели случайных графов, такие как модель Эрдеша-Реньи (ER) и модель Модель Уоттса-Строгаца (WS) не демонстрирует степенные законы. Модель Барабаши-Альберта — одна из нескольких предложенных моделей, генерирующих безмасштабные сети. Он включает в себя две важные общие концепции: рост и преференциальную привязанность . И рост, и преференциальная привязанность широко распространены в реальных сетях.

Рост означает, что количество узлов в сети со временем увеличивается.

Предпочтительное присоединение означает, что чем более связан узел, тем больше вероятность того, что он получит новые ссылки. Узлы с более высоким уровнем имеют более сильную способность захватывать ссылки, добавленные в сеть. Интуитивно, предпочтительную привязанность можно понять, если подумать о социальных сетях, объединяющих людей. Здесь связь от A к B означает, что человек A «знает» или «знаком» человека B. Сильно связанные узлы представляют известных людей с большим количеством отношений. Когда новичок входит в сообщество, он с большей вероятностью познакомится с одним из наиболее заметных людей, чем с относительно неизвестным. Модель BA была предложена исходя из предположения, что во Всемирной паутине новые страницы преимущественно ссылаются на хабы, то есть на очень известные сайты, такие как Google , а не на страницы, о которых почти никто не знает. Если кто-то выбирает новую страницу для ссылки, случайно выбирая существующую ссылку, вероятность выбора конкретной страницы будет пропорциональна ее степени. Модель BA утверждает, что это объясняет правило вероятности преимущественного прикрепления.

Позже модель Бьянкони-Барабаси решает эту проблему, вводя параметр «приспособленности». Предпочтительное присоединение — это пример цикла положительной обратной связи , в котором изначально случайные вариации (один узел изначально имел больше ссылок или начал накапливать ссылки раньше, чем другой) автоматически подкрепляются, тем самым значительно увеличивая различия. Это еще иногда называют эффектом Мэтью : « богатые становятся еще богаче ». См. также автокатализ .

Алгоритм

Шаги роста сети по модели Барабаси–Альберта ( $m_{0}=m=2$)

Единственным параметром в модели BA является $m$, положительное целое число. Сеть инициализируется сетью $m_{0}\geq m$ узлы.

На каждом шаге добавляйте один новый узел, затем производите выборку $m$ существующие вершины из сети с вероятностью, пропорциональной количеству связей, которые уже есть в существующих узлах (в исходных статьях не указано, как обрабатывать случаи, когда один и тот же существующий узел выбирается несколько раз). Формально вероятность $p_{i}$ что новый узел подключен к узлу $i$ является

$p_{i}={\frac {k_{i}}{\sum _{j}k_{j}}},$

где $k_{i}$ это степень узла $i$ и сумма производится по всем ранее существовавшим узлам $j$ (т.е. знаменатель дает удвоенное количество ребер в сети). Этот шаг можно выполнить, сначала равномерно выбрав одно ребро, а затем выбрав одну из двух вершин на ребре.

Сильно связанные узлы («концентраторы») имеют тенденцию быстро накапливать еще больше ссылок, в то время как узлы всего с несколькими ссылками вряд ли будут выбраны в качестве места назначения для новой ссылки. Новые узлы имеют «предпочтение» присоединяться к уже тесно связанным узлам.

Древовидная сеть, созданная по модели Барабаси-Альберта. Сеть состоит из 50 вершин с начальными степенями $m_{0}=1$.

Характеристики

Распределение степеней

Распределение степеней вершин графа BA с 200 000 узлов и 2 новыми ребрами на шаг. Построено в логарифмическом масштабе. Это следует степенному закону с показателем -2,78.

Распределение степеней, полученное в результате модели БА, является безмасштабным, в частности, оно представляет собой степенной закон вида

$P(k)\sim k^{-3}\,$

Распределение индекса Хирша

Было показано, что распределение индекса Хирша или индекса Хирша также не имеет масштаба и было предложено в качестве индекса лобби, который будет использоваться в качестве меры центральности.

$H(k)\sim k^{-6}\,$

Кроме того, аналитический результат для плотности узлов с индексом h 1 можно получить в случае, когда $m_{0}=1$

$H(1){\Big |}_{m_{0}=1}=4-\pi \,$

Корреляции степени узла

Корреляции между степенями связности узлов в модели BA развиваются спонтанно в зависимости от того, как развивается сеть. Вероятность, $n_{k\ell }$, поиска связи, соединяющей узел степени $k$ к родительскому узлу степени $\ell$ в модели БА для частного случая $m=1$ (дерево BA) определяется выражением

$n_{k\ell }={\frac {4\left(\ell -1\right)}{k\left(k+1\right)\left(k+\ell \right)\left(k+\ell +1\right)\left(k+\ell +2\right)}}+{\frac {12\left(\ell -1\right)}{k\left(k+\ell -1\right)\left(k+\ell \right)\left(k+\ell +1\right)\left(k+\ell +2\right)}}.$

Это подтверждает существование степенных корреляций, поскольку если бы распределения были некоррелированными, мы бы получили $n_{k\ell }=k^{-3}\ell ^{-3}$.

Для общего $m$, доля звеньев, соединяющих узел степени $k$ до узла степени $\ell$ является

$p(k,\ell )={\frac {2m(m+1)}{k(k+1)\ell (\ell +1)}}\left[1-{\frac {{\binom {2m+2}{m+1}}{\binom {k+\ell -2m}{\ell -m}}}{\binom {k+\ell +2}{\ell +1}}}\right].$

Кроме того, распределение степеней ближайших соседей $p(\ell \mid k)$, то есть распределение степеней соседей узла со степенью $k$, определяется

$p(\ell \mid k)={\frac {m(k+2)}{k\ell (\ell +1)}}\left[1-{\frac {{\binom {2m+2}{m+1}}{\binom {k+\ell -2m}{\ell -m}}}{\binom {k+\ell +2}{\ell +1}}}\right].$

Другими словами, если мы выберем узел со степенью $k$, а затем случайным образом выберет одного из его соседей, вероятность того, что этот случайно выбранный сосед будет иметь степень $\ell$ задается выражением $p(\ell |k)$ выше.

Коэффициент кластеризации

Аналитический результат для коэффициента кластеризации модели BA был получен Клеммом и Эгилусом. и доказано Боллобасом. Подход среднего поля для изучения коэффициента кластеризации применили Фрончак, Фрончак и Холист.

Такое поведение по-прежнему отличается от поведения сетей маленького мира, в которых кластеризация не зависит от размера системы.В случае иерархических сетей кластеризация как функция степени узла также подчиняется степенному закону:

$C(k)=k^{-1}.\,$

This result was obtained analytically by Dorogovtsev, Goltsev and Mendes.

Спектральные свойства

Спектральная плотность модели БА имеет форму, отличную от полукруглой спектральной плотности случайного графа. Он имеет форму треугольника, вершина которого лежит значительно выше полукруга, а края затухают по степенному закону. В (раздел 5.1) путем анализа моментов спектральной плотности как функции степенного показателя было доказано, что форма этой спектральной плотности не является точной треугольной функцией.

Динамическое масштабирование

Обобщенное распределение степеней $F(q,t)$ модели БА для $m=1$

Те же данные представлены в самоподобных координатах $t^{1/2}F(q,N)$ и $q/t^{1/2}$ и это дает отличный свернутый результат, показывающий, что $F(q,t)$ демонстрировать динамическое масштабирование.

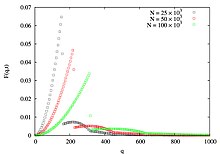
По определению, модель BA описывает явление, развивающееся во времени, и, следовательно, помимо ее свойства безмасштабности, можно также искать ее свойство динамического масштабирования.В узлах сети БА также можно охарактеризовать обобщенную степень $q$, продуктквадратного корня из времени рождения каждого узла и соответствующей им степени $k$, вместостепени $k$ в сети БА имеет значение только время рождения. Мы обнаруживаем, чтообобщенное распределение степеней $F(q,t)$ имеет некоторые нетривиальные особенности и демонстрирует динамическое масштабирование

$F(q,t)\sim t^{-1/2}\phi (q/t^{1/2}).$

Это означает, что отдельные сюжеты $F(q,t)$ против $q$ схлопнется в универсальную кривую, если мы построим график $F(q,t)t^{1/2}$ против $q/t^{1/2}$.

Предельные случаи

Модель А

Модель А сохраняет рост, но не включает привилегированную привязанность. Вероятность подключения нового узла к любому уже существующему узлу равна. Результирующее распределение степеней в этом пределе является геометрическим, что указывает на то, что одного роста недостаточно для создания безмасштабной структуры.

Модель Б

Модель Б сохраняет преференциальную привязанность, но исключает рост. Модель начинается с фиксированного количества отключенных узлов и добавляет ссылки, предпочтительно выбирая узлы высокой степени в качестве пунктов назначения ссылок. Хотя распределение степеней на ранних этапах моделирования выглядит безмасштабным, оно нестабильно и в конечном итоге становится почти гауссовым, когда сеть приближается к насыщению. Таким образом, одного только предпочтительного прикрепления недостаточно для создания структуры без масштабов.

Неспособность моделей A и B привести к безмасштабному распределению указывает на то, что рост и предпочтительное присоединение необходимы одновременно для воспроизведения стационарного степенного распределения, наблюдаемого в реальных сетях.

Нелинейная льготная привязанность

Основная статья: Non-linear_preferential_attachment

Модель BA можно рассматривать как частный случай более общей модели нелинейной предпочтительной привязанности (NLPA). Алгоритм NLPA идентичен модели BA с заменой вероятности прикрепления на более общую форму

$p_{i}={\frac {k_{i}^{\alpha }}{\sum _{j}k_{j}^{\alpha }}},$

где $\alpha$ является постоянным положительным показателем. Если $\alpha =1$NLPA сводится к модели BA и называется «линейной». Если $0<\alpha <1$NLPA называется «сублинейным», а распределение степеней сети имеет тенденцию к растянутому экспоненциальному распределению . Если $\alpha >1$NLPA называется «суперлинейным», и небольшое количество узлов подключается практически ко всем остальным узлам в сети. Для обоих $\alpha <1$ и $\alpha >1$, свойство безмасштабности сети нарушается в пределе бесконечного размера системы. Однако, если $\alpha$ лишь немного больше, чем $1$, NLPA может привести к тому, что распределения степеней временно кажутся свободными от масштабирования.

История

Предпочтительная привязанность впервые появилась в 1923 году в знаменитой модели урны, созданной венгерским математиком Дьёрдь Полья в 1923 году. Метод основных уравнений, который дает более прозрачный вывод, был применен к проблеме Гербертом А. Саймоном в 1955 году. в ходе исследований размеров городов и других явлений. Впервые его применил для объяснения частоты цитирования Дерек де Солла Прайс в 1976 году. Прайс был заинтересован в накоплении цитирований научных статей, и модель Прайса использовала «кумулятивное преимущество» (его название для преференциального прикрепления) для создания распределения с толстым хвостом. Говоря языком современной сети цитирования, модель Прайса создает направленную сеть, то есть версию модели Барабаши-Альберта. Название «предпочтительное присоединение» и нынешняя популярность моделей безмасштабных сетей связаны с работой Альберта-Ласло Барабаси и Реки Альберта , которые обнаружили, что аналогичный процесс присутствует в реальных сетях, и применили в 1999 году предпочтительное присоединение для объяснения численно наблюдаемые распределения степеней в сети.

См. также

• Модель Бьянкони – Барабаса
• процесс в китайском ресторане
• Сложные сети
• Модель Эрдеша – Реньи (ER)
• Модель Прайса
• Теория перколяции
• Безмасштабная сеть
• Сеть маленького мира
• Модель Уоттса и Строгаца

Внешние ссылки

• «Этот человек мог бы править миром»
• «Реализация Java для Барабаши-Альберта»
• «Создание графов модели Барабаши – Альберта в коде»