Безмасштабная сеть

| Часть серии о | ||||
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
| ||||
| Модели | ||||
| ||||
| ||||
Безмасштабная сеть — это сеть которой , распределение степеней подчиняется степенному закону , по крайней мере асимптотически. То есть доля P ( k ) узлов в сети, имеющих k соединений с другими узлами, соответствует большим значениям k как
где это параметр, значение которого обычно находится в диапазоне (при этом второй момент ( параметр масштаба ) бесконечно, но первый момент конечен), хотя иногда он может лежать за этими пределами. [1] [2] Название «безмасштабная» можно объяснить тем, что некоторые моменты распределения степеней не определены, поэтому сеть не имеет характерного масштаба или «размера».
Сообщается, что многие сети не имеют масштаба, хотя статистический анализ опроверг многие из этих утверждений и серьезно поставил под сомнение другие. [3] [4] Кроме того, некоторые утверждают, что просто знать, что распределение степеней имеет «толстый хвост», важнее, чем знать, является ли сеть безмасштабной в соответствии со статистически строгими определениями. [5] [6] Предпочтительное присоединение и модель приспособленности были предложены в качестве механизмов для объяснения предполагаемого степенного распределения степеней в реальных сетях. Альтернативные модели, такие как суперлинейное предпочтительное присоединение и предпочтительное присоединение второго соседа, могут создавать временные безмасштабные сети, но распределение степеней отклоняется от степенного закона, поскольку сети становятся очень большими. [7] [8]
История
[ редактировать ]Изучая сети цитирования между научными статьями, Дерек де Солла Прайс в 1965 году показал, что количество ссылок на статьи (т. е. количество полученных ими цитирований) имеет распределение с тяжелым хвостом , соответствующее распределению Парето или степенному закону , и таким образом, сеть цитирования не имеет масштаба. Однако он не использовал термин «безмасштабная сеть», который был придуман лишь несколько десятилетий спустя. В более поздней статье 1976 года Прайс также предложил механизм, объясняющий возникновение степенных законов в сетях цитирования, который он назвал «кумулятивным преимуществом», но который сегодня более известен под названием « предпочтительная привязанность » .
Недавний интерес к безмасштабным сетям начался в 1999 году с работы Альберта-Ласло Барабаши и Реки Альберт из Университета Нотр-Дам, которые нанесли на карту топологию части Всемирной паутины. [9] обнаружив, что некоторые узлы, которые они называли «концентраторами», имели гораздо больше соединений, чем другие, и что сеть в целом имела степенное распределение количества ссылок, подключающихся к узлу. Обнаружив, что несколько других сетей, в том числе некоторые социальные и биологические сети, также имеют распределение степеней с тяжелым хвостом, Барабаши и Река Альберт ввели термин «безмасштабная сеть», чтобы описать класс сетей, которые демонстрируют степенное распределение степеней. . Однако, изучая семь примеров сетей в социальных, экономических, технологических, биологических и физических системах, Амарал и др. не смогли найти безмасштабную сеть среди этих семи примеров. Только один из этих примеров, сеть киноактеров, имела распределение степеней P ( k ) в соответствии со степенным режимом для умеренных k , хотя в конечном итоге за этим степенным режимом последовал резкий срез, демонстрирующий экспоненциальное затухание для больших k . [10]
Барабаши и Река Альберт предложили генеративный механизм для объяснения появления степенных распределений, который они назвали « предпочтительной привязанностью » и который по существу аналогичен механизму, предложенному Прайсом. Аналитические решения этого механизма (также аналогичные решению Прайса) были представлены в 2000 году Дороговцевым, Мендесом и Самухиным. [11] и независимо Крапивским, Реднером и Лейвразом, а позже строго доказано математиком Белой Боллобасом . [12] Однако примечательно, что этот механизм создает только определенное подмножество сетей безмасштабного класса, и с тех пор было обнаружено множество альтернативных механизмов. [13]
История безмасштабных сетей также включает в себя некоторые разногласия. На эмпирическом уровне безмасштабная природа некоторых сетей была поставлена под сомнение. Например, три брата Фалуцос считали, что Интернет имеет степенное распределение степеней на основе трассировки данных ; однако было высказано предположение, что это иллюзия уровня 3, создаваемая маршрутизаторами, которые выглядят как узлы высокого уровня, скрывая при этом внутреннюю уровня 2 структуру AS , которые они соединяют. [14]
На теоретическом уровне были предложены уточнения абстрактного определения безмасштабности. Например, Ли и др. (2005) предложили потенциально более точную «безмасштабную метрику». Кратко, пусть G — граф с множеством ребер E и обозначает степень вершины (т. е. количество ребер, инцидентных ) к . Определять
Это максимизируется, когда узлы высокого уровня соединены с другими узлами высокого уровня. Теперь определите
где s max — максимальное значение s ( H ) для H в наборе всех графов с распределением степеней, идентичным G. распределению Это дает метрику от 0 до 1, где граф G с малым S ( G ) является «богатым по масштабу», а граф G с S ( G ) близким к 1 является «безмасштабным». Это определение отражает понятие самоподобия , подразумеваемое в названии «безмасштабный».
Обзор
[ редактировать ]Когда концепция «безмасштабности» была впервые введена в контексте сетей, [9] в первую очередь это относилось к конкретной характеристике: степенному распределению данной переменной. , выраженный как . Это свойство сохраняет свою форму при непрерывном масштабном преобразовании. , вызывая параллели с методами ренормгруппы в статистической теории поля. [15] [16]
Однако есть ключевое отличие. В статистической теории поля термин «масштаб» часто относится к размеру системы. В сфере сетей «масштаб» — это мера связности, обычно определяемая степенью узла, то есть количеством подключенных к нему ссылок. Сети с большим количеством узлов высокого уровня считаются более связными.
Степенное распределение степеней позволяет нам делать «безмасштабные» утверждения о преобладании узлов высокой степени. [17] Например, мы можем сказать, что «узлы со средней связностью в три раза встречаются вдвое реже, чем узлы со средней связностью». Конкретное числовое значение того, что представляет собой «средняя связность», становится неважным, будь то сто или миллион. [18]
Характеристики
[ редактировать ]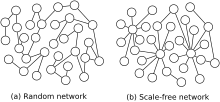
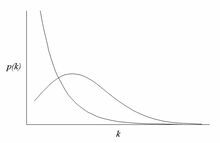
Наиболее примечательной характеристикой безмасштабной сети является относительная общность вершин со степенью, значительно превышающей среднюю. Узлы высшего уровня часто называют «концентраторами», и считается, что они служат определенным целям в своих сетях, хотя это во многом зависит от домена.
Кластеризация
[ редактировать ]Другой важной характеристикой безмасштабных сетей является распределение коэффициента кластеризации , которое уменьшается с увеличением степени узла. Это распределение также подчиняется степенному закону. Это означает, что узлы низкой степени принадлежат очень плотным подграфам, и эти подграфы связаны друг с другом через концентраторы. Рассмотрим социальную сеть, в которой узлами являются люди, а ссылками — отношения знакомств между людьми. Легко заметить, что люди склонны образовывать сообщества, т. е. небольшие группы, в которых все всех знают (такое сообщество можно представить как полный граф ). Кроме того, члены сообщества также имеют некоторые знакомые отношения с людьми за пределами этого сообщества. Однако некоторые люди связаны с большим количеством сообществ (например, знаменитости, политики). Этих людей можно считать центрами, ответственными за феномен маленького мира .
В настоящее время более конкретные характеристики безмасштабных сетей различаются в зависимости от генеративного механизма, используемого для их создания. Например, сети, созданные путем предпочтительного присоединения, обычно размещают вершины высокого уровня в середине сети, соединяя их вместе, образуя ядро, а узлы постепенно более низкого уровня составляют области между ядром и периферией. Случайное удаление даже большой части вершин очень мало влияет на общую связность сети, что позволяет предположить, что такие топологии могут быть полезны для безопасности , тогда как целевые атаки очень быстро разрушают связность. Другие безмасштабные сети, в которых вершины высокой степени расположены на периферии, не обладают этими свойствами. Аналогично, коэффициент кластеризации безмасштабных сетей может существенно различаться в зависимости от других топологических деталей.
Иммунизация
[ редактировать ]Вопрос о том, как иммунизировать эффективно масштабируемые свободные сети, которые представляют собой реалистичные сети, такие как Интернет и социальные сети, широко изучался. Одной из таких стратегий является иммунизация узлов наибольшей степени, т. е. целевые (намеренные) атаки, поскольку в этом случае p относительно высока, и для иммунизации требуется меньше узлов. Однако во многих реальных случаях глобальная структура недоступна и узлы наибольшей степени неизвестны.
Свойства случайного графа могут изменяться или оставаться неизменными при преобразованиях графа. Машаги А. и др., например, продемонстрировали, что преобразование, которое преобразует случайные графы в их двойные по ребрам графы (или линейные графы), создает ансамбль графов с почти таким же распределением степеней, но с корреляциями степеней и значительно более высокой кластеризацией. коэффициент. Безмасштабные графы как таковые остаются безмасштабными при таких преобразованиях. [19]
Примеры
[ редактировать ]Хотя многие реальные сети считаются безмасштабными, доказательства часто остаются неубедительными, в первую очередь из-за растущего понимания более строгих методов анализа данных. [3] Таким образом, безмасштабность многих сетей все еще обсуждается научным сообществом. Вот несколько примеров сетей, которые, как утверждается, являются безмасштабными:
- Некоторые социальные сети , включая сети для совместной работы. Двумя примерами, которые были тщательно изучены, являются сотрудничество киноактеров в фильмах и соавторство статей математиками .
- Многие виды компьютерных сетей , включая Интернет и веб-графику Всемирной паутины .
- Некоторые финансовые сети, такие как сети межбанковских платежей. [20] [21]
- белок-белкового взаимодействия . Сети
- Семантические сети . [22]
- Сети авиакомпаний.

Безмасштабная топология была также обнаружена в высокотемпературных сверхпроводниках. [23] Свойства высокотемпературного сверхпроводника — соединения, в котором электроны подчиняются законам квантовой физики и текут идеально синхронно, без трения — по-видимому, связаны с фрактальным расположением, казалось бы, случайных атомов кислорода и искажением решетки. [24]
Недавно была предложена заполняющая пространство ячеистая структура, взвешенная плоская стохастическая решетка (WPSL), распределение координационного числа которой подчиняется степенному закону. Это означает, что в решетке есть несколько блоков, имеющих удивительно большое количество соседей, с которыми они имеют общие границы. Его строительство начинается с инициатора, скажем,квадрат единичной площади и генератор, который случайным образом делит его на четыре блока. После этого последовательно включается генератор.снова и снова, чтобы только один из доступных блоков был выбран предпочтительно по отношению к их областям. Это приводит к разделению площади на все более мелкие взаимоисключающие прямоугольные блоки. Двойной WPSL (DWPSL), который получается путем замены каждого блока узлом в его центре и каждой общей границы. между блоками с ребром, соединяющим две соответствующие вершины, представляет собой сеть, распределение степеней которой следуетстепенной закон. [25] [26] Причина этого в том, что он растет в соответствии с правилом модели привязанности, основанной на посредничестве , которое также воплощает в себе правило предпочтительной привязанности, но замаскированное.
Генеративные модели
[ редактировать ]Безмасштабные сети возникают не случайно. Эрдеш и Реньи (1960) исследовали модель роста графов, в которой на каждом шаге два узла выбираются равномерно случайным образом и между ними вставляется связь. Свойства этих случайных графов отличаются от свойств, обнаруженных в безмасштабных сетях, и поэтому необходима модель для этого процесса роста.
Наиболее широко известной генеративной моделью для подмножества безмасштабных сетей является генеративная модель Барабаши и Альберта (1999) , в которой каждая новая веб-страница создает ссылки на существующие веб-страницы с распределением вероятностей, которое не является равномерным, нопропорционально текущему уровню веб-страниц. Эта модель была первоначально изобретена Дереком Дж. де Солла Прайсом в 1965 году под термином «кумулятивное преимущество» , но не достигла популярности, пока Барабаси заново не открыл результаты под своим нынешним названием ( модель BA ). Согласно этому процессу, страница с большим количеством входящих ссылок будет привлекать больше входящих ссылок, чем обычная страница. Это генерирует степенной закон, но полученный граф отличается от фактического веб-графа другими свойствами, такими как наличие небольших тесно связанных сообществ. Были предложены и изучены более общие модели и характеристики сети. Например, Пачон и др. (2018) предложили вариант генеративной модели «богатые становятся богаче» , которая учитывает два разных правила прикрепления: механизм преимущественного прикрепления и единый выбор только для самых последних узлов. [27] Рецензию см. в книге Дороговцева и Мендеса . [ нужна ссылка ] Некоторые механизмы, такие как сверхлинейное предпочтительное присоединение и присоединение второго соседа, создают сети, которые временно не имеют масштаба, но отклоняются от степенного закона по мере роста сетей. [7] [8]
Несколько иная генеративная модель веб-ссылок была предложена Pennock et al. (2002). Они исследовали сообщества, интересующиеся определенной темой, такие как домашние страницы университетов, государственных компаний, газет или ученых, и отбросили основные центры Интернета. В этом случае распределение ссылок уже не было степенным законом, а напоминало нормальное распределение . Основываясь на этих наблюдениях, авторы предложили генеративную модель, которая сочетает предпочтительную привязанность с базовой вероятностью получения ссылки.
Другая генеративная модель — это модель копирования , изученная Кумаром и др. [28] (2000),в котором новые узлы случайным образом выбирают существующий узел и копируют часть ссылок существующего узла. Это также порождает степенной закон.
Есть два основных компонента, которые объясняют появление степенного распределения в модели Барабаши-Альберта : рост и преференциальная привязанность. [29] Под «ростом» подразумевается процесс роста, при котором в течение длительного периода времени новые узлы присоединяются к уже существующей системе, сети (например, Всемирной паутине, которая за 10 лет выросла на миллиарды веб-страниц). Наконец, под «предпочтительным присоединением» подразумевается, что новые узлы предпочитают подключаться к узлам, которые уже имеют большое количество связей с другими. Таким образом, существует более высокая вероятность того, что все больше и больше узлов будут связываться с тем узлом, который уже имеет много ссылок, что в конечном итоге приведет этот узел к хабу . [9] В зависимости от сети концентраторы могут быть ассортативными или неассортативными. Ассортативность можно обнаружить в социальных сетях, в которых люди с хорошими связями/известные люди, как правило, лучше узнают друг друга. Дисассортативность может быть обнаружена в технологических (Интернет, Всемирная паутина) и биологических (взаимодействие белков, метаболизм) сетях. [29]
Однако рост сетей (добавление новых узлов) не является необходимым условием для создания безмасштабной сети (см. Дангалчев [30] ). Одна из возможностей (Калдарелли и др., 2002) состоит в том, чтобы рассматривать структуру как статическую и рисовать связь между вершинами в соответствии с конкретным свойством двух задействованных вершин. После определения статистического распределения этих свойств вершин (пригодностей) оказывается, что в некоторых случаях статические сети также приобретают безмасштабные свойства.
Обобщенная безмасштабная модель
[ редактировать ]Произошел всплеск активности в моделировании безмасштабных сложных сетей . Рецепт Барабаси и Альберта [31] последовало несколько вариаций и обобщений [32] [33] [34] [35] [27] и переработка предыдущих математических работ. [36]
С современной точки зрения, если сложная сеть имеет степенное распределение любой из своих метрик, она обычно считается безмасштабной сетью. Аналогично, любая модель с этой особенностью называется безмасштабной моделью. [17]
Функции
[ редактировать ]Многие реальные сети (приблизительно) безмасштабны и, следовательно, для их описания требуются безмасштабные модели. В схеме Прайса для построения безмасштабной модели необходимы два ингредиента:
1. Добавление или удаление узлов . Обычно мы концентрируемся на расширении сети, то есть добавлении узлов.
2. Предпочтительная привязанность : вероятность что новые узлы будут подключены к «старому» узлу.
Обратите внимание, что некоторые модели (см. Дангалчев [30] иФитнес-модель ниже) может работать и статически, без изменения количества узлов. Следует также иметь в виду, что тот факт, что модели «предпочтительного прикрепления» приводят к появлению безмасштабных сетей, не доказывает, что это механизм, лежащий в основе эволюции реальных безмасштабных сетей, поскольку могут существовать различные механизмы в работать в реальных системах, которые, тем не менее, приводят к масштабированию.
Примеры
[ редактировать ]Было предпринято несколько попыток создать безмасштабные сетевые свойства. Вот несколько примеров:
Модель Барабаши – Альберта
[ редактировать ]Модель Барабаши-Альберта , ненаправленная версия модели Прайса, имеет линейное предпочтительное присоединение. и добавляет один новый узел на каждом временном шаге.
(Обратите внимание, еще одна общая особенность в реальных сетях такое , т.е. существует ненулевая вероятность того, чтоновый узел присоединяется к изолированному узлу. Таким образом, в целом имеет форму , где — начальная привлекательность узла.)
Двухуровневая сетевая модель
[ редактировать ]Дангалчев (см. [30] ) строит 2-L модель, учитывая важность каждого из соседей целевого узла в предпочтительном присоединении. Привлекательность узла в модели 2-L зависит не только от количества связанных с ним узлов, но и от количества связей в каждом из этих узлов.
где C — коэффициент от 0 до 1.
Вариант модели 2-L, модель k2, в которой первый и второй соседние узлы в равной степени способствуют привлекательности целевого узла, демонстрирует появление переходных безмасштабных сетей. [8] В модели k2 распределение степеней выглядит приблизительно безмасштабным, пока сеть относительно мала, но значительные отклонения от безмасштабного режима возникают по мере увеличения сети. Это приводит к тому, что относительная привлекательность узлов разной степени меняется со временем, что также наблюдается в реальных сетях.
Модель прикрепления на основе медиации (MDA)
[ редактировать ]В модели вложений, управляемых посредничеством (MDA) , новый узел поставляется с ребра случайным образом выбирают существующий связный узел, а затем соединяются не с ним, а с своих соседей, также выбранных случайно. Вероятность что узел существующего выбранного узла
Фактор является обратной величиной среднего гармонического(IHM) степеней соседи узла . Обширные численные исследования показывают, что примерно в течение среднее значение IHM в большом предел становится константой, что означает . Это означает, что чем вышесвязей (уровня) узла, тем выше его шансы получить больше связей, поскольку они могут бытьдостигается большим количеством способов через посредников, которые, по сути, воплощают интуитивныйидея механизма «богатые становятся богаче» (или правила преимущественной привязанности модели Барабаси-Альберта). Таким образом, можно увидеть, что сеть MDA следуетправило ПА, но замаскированное. [37]
Однако для он описывает механизм «победитель получает все», поскольку мы обнаруживаем, что почти из всех узлов имеет степень один, а один — сверхбогатый по степени. Как стоимость увеличивается, неравенство между сверхбогатыми и бедными уменьшается, и по мере того, как мы обнаруживаем переход от механизма «богатые становятся супербогаче» к механизму «богатые становятся еще богаче».
Нелинейная льготная привязанность
[ редактировать ]Модель Барабаши – Альберта предполагает, что вероятность что узел присоединяется к узлу пропорциональна степени узла . Это предположение включает в себя две гипотезы: во-первых, что зависит от , в отличие от случайных графов, в которых и во-вторых, что функциональная форма линейна по .
При нелинейной преимущественной привязанности форма не является линейным, и недавние исследования показали, что распределение степеней сильно зависит от формы функции
Krapivsky, Redner, and Leyvraz [34] продемонстрировать, что безмасштабная природа сети разрушается из-за нелинейного предпочтительного присоединения. Единственный случай, когда топология сети немасштабна, — это случай, когда предпочтительное присоединение асимптотически линейно, т.е. как . В этом случае уравнение скорости приводит к
Таким образом, показатель степени распределения можно настроить на любое значение от 2 до . [ нужны разъяснения ]
Иерархическая сетевая модель
[ редактировать ]Иерархические сетевые модели по своей конструкции не масштабируются и имеют высокую кластеризацию узлов. [38]
Итеративное построение приводит к иерархической сети. Начиная с полностью связанного кластера из пяти узлов, мы создаем четыре идентичные реплики, соединяющие периферийные узлы каждого кластера с центральным узлом исходного кластера. Отсюда мы получаем сеть из 25 узлов ( N = 25).Повторяя тот же процесс, мы можем создать еще четыре реплики исходного кластера — четыре периферийных узла каждого из них подключаются к центральному узлу узлов, созданных на первом этапе. Это дает N = 125, и процесс может продолжаться бесконечно.
Фитнес-модель
[ редактировать ]Идея состоит в том, что связь между двумя вершинами назначается не случайно с вероятностью p, одинаковой для всех пар вершин. Скорее, для каждая вершина j имеет внутреннюю пригодность x j , и связь между вершинами i и j создается с вероятностью . [39] В случае Всемирной торговой сети можно реконструировать все свойства, используя в качестве показателей приспособленности страны их ВВП и принимая
Гиперболические геометрические графы
[ редактировать ]Предполагая, что сеть имеет базовую гиперболическую геометрию, можно использовать структуру пространственных сетей для генерации безмасштабных распределений степеней. Это неоднородное распределение степеней затем просто отражает отрицательную кривизну и метрические свойства базовой гиперболической геометрии. [41]
Двойное преобразование ребер для создания графов без масштабирования с желаемыми свойствами.
[ редактировать ]Начав с безмасштабных графов с низкой степенью корреляции и коэффициентом кластеризации, можно создать новые графы с гораздо более высокой степенью корреляции и коэффициентами кластеризации, применив двойственное преобразование. [19]
Модель единых льготных вложений (модель UPA)
[ редактировать ]Модель UPA представляет собой вариант модели предпочтительной привязанности (предложенной Пахоном и др.), которая учитывает два разных правила привязанности: механизм предпочтительной привязанности (с вероятностью 1-p), который подчеркивает систему «богатые становятся богаче», и единый выбор. (с вероятностью p) для самых последних узлов. Эта модификация интересна для изучения устойчивости безмасштабного поведения распределения степеней. Аналитически доказано, что асимптотически степенное распределение степеней сохраняется. [27]
Безмасштабные идеальные сети
[ редактировать ]В контексте теории сетей безмасштабная идеальная сеть — это случайная сеть с распределением степеней, соответствующим безмасштабному распределению плотности идеального газа . Эти сети способны воспроизводить распределение по размерам городов и результаты выборов, раскрывая распределение социальных групп по размерам с помощью теории информации в сложных сетях, когда к сети применяется процесс конкурентного роста кластеров. [42] [43] В моделях безмасштабных идеальных сетей можно продемонстрировать, что число Данбара является причиной явления, известного как « шесть степеней разделения ».
Новые характеристики
[ редактировать ]Для безмасштабной сети с узлы и показатель степени , индуцированный подграф, построенный из вершин со степенями, большими, чем представляет собой безмасштабную сеть с , почти наверняка . [44]
Оценка показателя степенного закона
[ редактировать ]Оценка показателя степени безмасштабной сети обычно выполняется с использованием оценки максимального правдоподобия со степенями нескольких узлов с равномерной выборкой. [3] Однако, поскольку при равномерной выборке недостаточно выборок из важного тяжелого хвоста степенного распределения степеней, этот метод может привести к большой погрешности и дисперсии. Недавно было предложено отбирать случайных друзей (то есть случайные концы случайных связей), которые с большей вероятностью происходят из хвоста распределения степеней в результате парадокса дружбы . [45] [46] Теоретически оценка максимального правдоподобия со случайными друзьями приводит к меньшему смещению и меньшей дисперсии по сравнению с классическим подходом, основанным на равномерной выборке. [46]
См. также
[ редактировать ]- Случайный график – график, созданный случайным процессом.
- Модель Эрдеша – Реньи - две тесно связанные модели для создания случайных графов.
- Нелинейная льготная привязанность
- Конденсация Бозе-Эйнштейна (теория сетей) - модель в сетевой науке.
- Масштабная инвариантность - характеристики, которые не изменяются, если масштабы длины или энергии умножаются на общий коэффициент.
- Сложная сеть - сеть с нетривиальными топологическими особенностями.
- Webgraph – график связанных веб-страниц.
- Модель Барабаши – Альберта – Алгоритм создания безмасштабной сети
- Модель Бьянкони-Барабаси - модель в сетевых науках.
Ссылки
[ редактировать ]- ^ Оннела, Ж.-П.; Сарамаки, Дж.; Хивонен, Дж.; Сабо, Г.; Лазер, Д.; Каски, К.; Кертес, Дж.; Барабаси, А.-Л. (2007). «Структура и сильные стороны сетей мобильной связи» . Труды Национальной академии наук . 104 (18): 7332–7336. arXiv : физика/0610104 . Бибкод : 2007PNAS..104.7332O . дои : 10.1073/pnas.0610245104 . ПМК 1863470 . ПМИД 17456605 .
- ^ Чороманский, К.; Матушак, М.; Мишкиш, Дж. (2013). «Безмасштабный граф с преимущественным присоединением и развивающейся внутренней структурой вершин» . Журнал статистической физики . 151 (6): 1175–1183. Бибкод : 2013JSP...151.1175C . дои : 10.1007/s10955-013-0749-1 .
- ^ Jump up to: а б с Клосет, Аарон; Косма Рохилла Шализи; М.Э. Дж. Ньюман (2009). «Степенное распределение в эмпирических данных». Обзор СИАМ . 51 (4): 661–703. arXiv : 0706.1062 . Бибкод : 2009SIAMR..51..661C . дои : 10.1137/070710111 . S2CID 9155618 .
- ^ Бройдо, Анна; Аарон Клаузет (04 марта 2019 г.). «Безмасштабные сети встречаются редко» . Природные коммуникации . 10 (1): 1017. arXiv : 1801.03400 . Бибкод : 2019NatCo..10.1017B . дои : 10.1038/s41467-019-08746-5 . ПМК 6399239 . ПМИД 30833554 .
- ^ Холм, Петтер (декабрь 2019 г.). «Редко и везде: Перспективы безмасштабных сетей» . Природные коммуникации . 10 (1): 1016. Бибкод : 2019NatCo..10.1016H . дои : 10.1038/s41467-019-09038-8 . ПМК 6399274 . ПМИД 30833568 .
- ^ Штумпф, магистр здравоохранения; Портер, Массачусетс (10 февраля 2012 г.). «Критические истины о степенных законах». Наука . 335 (6069): 665–666. Бибкод : 2012Sci...335..665S . дои : 10.1126/science.1216142 . ПМИД 22323807 . S2CID 206538568 .
- ^ Jump up to: а б Крапивский, Павел; Крюков, Дмитрий (21 августа 2008 г.). «Безмасштабные сети как предасимптотические режимы суперлинейного предпочтительного прикрепления». Физический обзор E . 78 (2): 026114. arXiv : 0804.1366 . Бибкод : 2008PhRvE..78b6114K . дои : 10.1103/PhysRevE.78.026114 . ПМИД 18850904 . S2CID 14292535 .
- ^ Jump up to: а б с Фалькенберг, Макс; Ли, Чон Хек; Амано, Сюн-ичи; Огава, Кен-итиро; Яно, Кадзуо; Мияке, Ёсихиро; Эванс, Тим С.; Кристенсен, Ким (18 июня 2020 г.). «Определение временной зависимости роста сети» . Обзор физических исследований . 2 (2): 023352. arXiv : 2001.09118 . Бибкод : 2020PhRvR...2b3352F . doi : 10.1103/PhysRevResearch.2.023352 .
- ^ Jump up to: а б с Барабаши, Альберт-Ласло ; Альберт, Река. (15 октября 1999 г.). «Появление масштабирования в случайных сетях». Наука . 286 (5439): 509–512. arXiv : cond-mat/9910332 . Бибкод : 1999Sci...286..509B . дои : 10.1126/science.286.5439.509 . МР 2091634 . ПМИД 10521342 . S2CID 524106 .
- ^ Среди семи примеров, изученных Амаралом и др., шесть из них были одномасштабными, и единственный пример iii - сеть киноактеров имела режим степенного закона, за которым следовало резкое ограничение. Ни один из примеров Амарала и др. не подчинялся режиму степенного закона при больших k , т.е. ни один из этих семи примеров не оказался безмасштабным. См. особенно начало раздела обсуждения Амарал ЛАН, Скала А, Бартелеми М, Стэнли Х.Э. (2000). «Классы сетей маленького мира» . ПНАС . 97 (21): 11149–52. arXiv : cond-mat/0001458 . Бибкод : 2000PNAS...9711149A . дои : 10.1073/pnas.200327197 . ПМК 17168 . ПМИД 11005838 .
- ^ Дороговцев С.; Мендес, Дж.; Самухин, А. (2000). «Структура растущих сетей с преимущественным связыванием». Письма о физических отзывах . 85 (21): 4633–4636. arXiv : cond-mat/0004434 . Бибкод : 2000PhRvL..85.4633D . дои : 10.1103/PhysRevLett.85.4633 . ПМИД 11082614 . S2CID 118876189 .
- ^ Боллобас, Б. ; Риордан, О.; Спенсер, Дж.; Туснади, Г. (2001). «Последовательность степеней безмасштабного случайного графового процесса». Случайные структуры и алгоритмы . 18 (3): 279–290. дои : 10.1002/rsa.1009 . МР 1824277 . S2CID 1486779 .
- ^ Дороговцев С.Н.; Мендес, JFF (2002). «Эволюция сетей». Достижения физики . 51 (4): 1079–1187. arXiv : cond-mat/0106144 . Бибкод : 2002AdPhy..51.1079D . дои : 10.1080/00018730110112519 . S2CID 429546 .
- ^ Виллингер, Уолтер ; Дэвид Олдерсон; Джон К. Дойл (май 2009 г.). «Математика и Интернет: источник огромной путаницы и большого потенциала» (PDF) . Уведомления АМС . 56 (5). Американское математическое общество: 586–599. Архивировано (PDF) из оригинала 15 мая 2011 г. Проверено 3 февраля 2011 г.
- ^ Ицыксон, Клод; Друфф, Жан-Мишель (1989). Статистическая теория поля: Том 1, От броуновского движения к перенормировке и калибровочной теории решетки (1-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-34058-8 .
- ^ Ицыксон, Клод; Друфф, Жан-Мишель (1989). Статистическая теория поля: Том 2, Сильная связь, методы Монте-Карло, конформная теория поля и случайные системы (1-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-37012-7 .
- ^ Jump up to: а б Мэн, Сянъи; Чжоу, Бинь (2023). «Безмасштабные сети за пределами степенного распределения степеней». Хаос, солитоны и фракталы . 176 : 114173. arXiv : 2310.08110 . Бибкод : 2023CSF...17614173M . дои : 10.1016/j.chaos.2023.114173 . S2CID 263909425 .
- ^ Танака, Рэйко (2005). «Метаболические сети с богатым масштабом». Физ. Преподобный Летт . 94 (16): 168101. Бибкод : 2005PhRvL..94p8101T . doi : 10.1103/PhysRevLett.94.168101 . ПМИД 15904266 .
- ^ Jump up to: а б Рамезанпур, А.; Каримипур, В.; Машаги, А. (2003). «Генерация коррелированных сетей из некоррелированных». Физ. Преподобный Е. 67 (4): 046107. arXiv : cond-mat/0212469 . Бибкод : 2003PhRvE..67d6107R . дои : 10.1103/PhysRevE.67.046107 . ПМИД 12786436 . S2CID 33054818 .
- ^ Де Маси, Джулия; и др. (2006). «Фитнес-модель для итальянского межбанковского денежного рынка». Физический обзор E . 74 (6): 066112. arXiv : физика/0610108 . Бибкод : 2006PhRvE..74f6112D . дои : 10.1103/PhysRevE.74.066112 . ПМИД 17280126 . S2CID 30814484 .
- ^ Сорамаки, Киммо; и др. (2007). «Топология межбанковских платежных потоков». Физика А: Статистическая механика и ее приложения . 379 (1): 317–333. Бибкод : 2007PhyA..379..317S . дои : 10.1016/j.physa.2006.11.093 . hdl : 10419/60649 .
- ^ Стиверс, Марк; Джошуа Б. Тененбаум (2005). «Крупномасштабная структура семантических сетей: статистический анализ и модель семантического роста». Когнитивная наука . 29 (1): 41–78. arXiv : cond-mat/0110012 . дои : 10.1207/s15516709cog2901_3 . ПМИД 21702767 . S2CID 6000627 .
- ^ Фратини, Микела; Почча, Никола; Риччи, Алессандро; Кампи, Гаэтано; Бургаммер, Манфред; Эппли, Габриэль; Бьянкони, Антонио (2010). «Безмасштабная структурная организация межузельных атомов кислорода в La2CuO4+y». Природы . 466 (7308): 841–4. arXiv : 1008.2015 . Бибкод : 2010Natur.466..841F . дои : 10.1038/nature09260 . ПМИД 20703301 . S2CID 4405620 .
- ^ Почча, Никола; Риччи, Алессандро; Кампи, Гаэтано; Фратини, Микела; Пури, Алессандро; Ди Джоаккино, Даниэле; Марчелли, Август; Рейнольдс, Майкл; Бургаммер, Манфред; Сайни, Науранг Л.; Эппли, Габриэль; Бьянкони, Антонио (2012). «Оптимальная неоднородность локальных искажений решетки в La2CuO4+y» . ПНАС . 109 (39): 15685–15690. arXiv : 1208.0101 . Бибкод : 2012PNAS..10915685P . дои : 10.1073/pnas.1208492109 . ПМЦ 3465392 . ПМИД 22961255 .
- ^ Хасан, МК; Хасан, МЗ; Павел, Н.И. (2010). «Топология безмасштабной сети и мультифрактальность во взвешенной планарной стохастической решетке» . Новый журнал физики . 12 (9): 093045. arXiv : 1008.4994 . Бибкод : 2010NJPh...12i3045H . дои : 10.1088/1367-2630/12/9/093045 .
- ^ Хасан, МК; Хасан, МЗ; Павел, Н.И. (2010). «Безмасштабный беспорядок координационного числа и мультифрактальный беспорядок размеров в взвешенной плоской стохастической решетке». Ж. Физ.: Конф. Сер . 297 :01.
- ^ Jump up to: а б с Пашон, Анжелика; Сасердот, Лаура; Ян, Шуи (2018). «Безмасштабное поведение сетей при наличии преимущественных и единых правил присоединения». Физика D: Нелинейные явления . 371 : 1–12. arXiv : 1704.08597 . Бибкод : 2018PhyD..371....1P . дои : 10.1016/j.physd.2018.01.005 . S2CID 119320331 .
- ^ Кумар, Рави; Рагхаван, Прабхакар (2000). Стохастические модели для веб-графа (PDF) . Основы информатики, 41-й ежегодный симпозиум. стр. 57–65. дои : 10.1109/SFCS.2000.892065 . Архивировано (PDF) из оригинала 3 марта 2016 г. Проверено 10 февраля 2016 г.
- ^ Jump up to: а б Барабаши, Альберт-Ласло ; Золтан Н., Олтвай. (2004). «Сетевая биология: понимание функциональной организации клетки». Обзоры природы Генетика . 5 (2): 101–113. дои : 10.1038/nrg1272 . ПМИД 14735121 . S2CID 10950726 .
- ^ Jump up to: а б с Дангалчев, Чавдар (июль 2004 г.). «Модели генерации безмасштабных сетей» . Физика А: Статистическая механика и ее приложения . 338 (3–4): 659–671. Бибкод : 2004PhyA..338..659D . дои : 10.1016/j.physa.2004.01.056 .
- ^ Барабаши, А.-Л. и Р. Альберт, Science 286 , 509 (1999).
- ^ Р. Альберт и А. Л. Барабаси, Phys. Преподобный Летт. 85 , 5234 (2000).
- ^ S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhim, cond-mat/0011115.
- ^ Jump up to: а б П. Л. Крапивский, С. Реднер, Ф. Лейвраз, Phys. Преподобный Летт. 85 , 4629 (2000).
- ^ Б. Тадич, Physica A 293 , 273 (2001).
- ^ С. Бомхольдт и Х. Эбель, cond-mat/0008465; Г. А. Симон, Биметрика 42 , 425 (1955).
- ^ Хасан, МК; Ислам, Лиана; Арефинул Хак, Сайед (2017). «Распределение степеней, распределение по рангам и сохранение лидерства в сетях привязанностей, основанных на посредничестве». Физика А. 469 : 23–30. arXiv : 1411.3444 . Бибкод : 2017PhyA..469...23H . дои : 10.1016/j.physa.2016.11.001 . S2CID 51976352 .
- ^ Равас, Э.; Барабаши (2003). «Иерархическая организация в сложных сетях». Физ. Преподобный Е. 67 (2): 026112. arXiv : cond-mat/0206130 . Бибкод : 2003PhRvE..67b6112R . дои : 10.1103/physreve.67.026112 . ПМИД 12636753 . S2CID 17777155 .
- ^ Кальдарелли, Дж.; и др. (2002). «Безмасштабные сети с различной внутренней пригодностью вершин» (PDF) . Физ. Преподобный Летт . 89 (25): 258702. Бибкод : 2002PhRvL..89y8702C . дои : 10.1103/physrevlett.89.258702 . ПМИД 12484927 .
- ^ Гарлашелли, Д.; и др. (2004). «Топологические свойства Всемирной торговой сети, зависящие от фитнеса». Физ. Преподобный Летт . 93 (18): 188701. arXiv : cond-mat/0403051 . Бибкод : 2004PhRvL..93r8701G . doi : 10.1103/physrevlett.93.188701 . ПМИД 15525215 . S2CID 16367275 .
- ^ Крюков Дмитрий; Пападопулос, Фрагкискос; Кицак, Максим; Вахдат, Амин; Богунья, Мариан (2010). «Гиперболическая геометрия сложных сетей». Физический обзор E . 82 (3): 036106. arXiv : 1006.5169 . Бибкод : 2010PhRvE..82c6106K . дои : 10.1103/PhysRevE.82.036106 . ПМИД 21230138 . S2CID 6451908 .
- ^ А. Эрнандо; Д. Виллуэндас; К. Весперинас; М. Абад; А. Пластино (2009). «Раскрытие размера социальных групп с помощью теории информации в сложных сетях». arXiv : 0905.3704 [ physical.soc-ph ]. , представлено в Европейский физический журнал B
- ^ Андре А. Морейра; Деметриус Р. Паула; Раймундо Н. Коста Фильо; Хосе С. Андраде-младший (2006). «Конкурентоспособный рост кластеров в сложных сетях». Физический обзор E. 73 (6): 065101. arXiv : cond-mat/0603272 . Бибкод : 2006PhRvE..73f5101M . дои : 10.1103/PhysRevE.73.065101 . ПМИД 16906890 . S2CID 45651735 .
- ^ Хейдари, Х.; Тахери, С.М.; Каве, К. (2018). «Распределенный максимальный независимый набор в безмасштабных сетях». arXiv : 1804.02513 [ cs.DC ].
- ^ Эом, Ён-Хо; Джо, Ханг Хён (11 мая 2015 г.). «Хвостовая область: использование друзей для оценки тяжелых хвостов распределений степеней в крупномасштабных сложных сетях» . Научные отчеты . 5 (1): 9752. arXiv : 1411,6871 . Бибкод : 2015NatSR...5E9752E . дои : 10.1038/srep09752 . ISSN 2045-2322 . ПМЦ 4426729 . ПМИД 25959097 .
- ^ Jump up to: а б Неттасингхе, Буддика; Кришнамурти, Викрам (19 мая 2021 г.). «Оценка максимального правдоподобия степенных распределений степеней с помощью выборки на основе парадокса дружбы» . Транзакции ACM по извлечению знаний из данных . 15 (6): 1–28. arXiv : 1908.00310 . дои : 10.1145/3451166 . ISSN 1556-4681 .
Дальнейшее чтение
[ редактировать ]- Альберт Р.; Барабаши А.-Л. (2002). «Статистическая механика сложных сетей» . Преподобный Мод. Физ . 74 (1): 47–97. arXiv : cond-mat/0106096 . Бибкод : 2002РвМП...74...47А . дои : 10.1103/RevModPhys.74.47 . S2CID 60545 .
- Амарал ЛАН, Скала А, Бартелеми М, Стэнли Х.Э. (2000). «Классы сетей маленького мира» . ПНАС . 97 (21): 11149–52. arXiv : cond-mat/0001458 . Бибкод : 2000PNAS...9711149A . дои : 10.1073/pnas.200327197 . ПМК 17168 . ПМИД 11005838 .
- Барабаши, Альберт-Ласло (2004). Связано: как все связано со всем остальным . Персей Паб. ISBN 0-452-28439-2 .
- Барабаши, Альберт-Ласло; Бонабо, Эрик (май 2003 г.). «Безмасштабные сети» (PDF) . Научный американец . 288 (5): 50–9. Бибкод : 2003SciAm.288e..60B . doi : 10.1038/scientificamerican0503-60 . ПМИД 12701331 .
- Дэн Браха; Янир Бар-Ям (2004). «Топология крупномасштабных сетей решения инженерных задач» (PDF) . Физ. Преподобный Е. 69 (1): 016113. Бибкод : 2004PhRvE..69a6113B . дои : 10.1103/PhysRevE.69.016113 . ПМИД 14995673 . S2CID 1001176 .
- Калдарелли Г. « Безмасштабные сети» Oxford University Press, Оксфорд (2007).
- Кальдарелли Г.; Капоччи А.; Де Лос Риос П.; Муньос М.А. (2002). «Безмасштабные сети с различной внутренней пригодностью вершин». Письма о физических отзывах . 89 (25): 258702. arXiv : cond-mat/0207366 . Бибкод : 2002PhRvL..89y8702C . doi : 10.1103/PhysRevLett.89.258702 . ПМИД 12484927 .
- Дангалчев, Ч. (2004). «Модели генерации безмасштабных сетей» . Физика А. 338 (3–4): 659–671. Бибкод : 2004PhyA..338..659D . дои : 10.1016/j.physa.2004.01.056 .
- Дороговцев С.Н.; Мендес, JFF; Самухин, АН (2000). «Структура растущих сетей: точное решение модели Барабаши-Альберта». Физ. Преподобный Летт . 85 (21): 4633–6. arXiv : cond-mat/0004434 . Бибкод : 2000PhRvL..85.4633D . doi : 10.1103/PhysRevLett.85.4633 . ПМИД 11082614 . S2CID 118876189 .
- Дороговцев С.Н.; Мендес, JFF (2003). Эволюция сетей: от биологических сетей к Интернету и WWW . Издательство Оксфордского университета. ISBN 0-19-851590-1 .
- Дороговцев С.Н.; Гольцев А.В.; Мендес, JFF (2008). «Критические явления в сложных сетях». Преподобный Мод. Физ . 80 (4): 1275–1335. arXiv : 0705.0010 . Бибкод : 2008РвМП...80.1275Д . дои : 10.1103/RevModPhys.80.1275 . S2CID 3174463 .
- Дороговцев С.Н.; Мендес, JFF (2002). «Эволюция сетей». Достижения физики . 51 (4): 1079–1187. arXiv : cond-mat/0106144 . Бибкод : 2002AdPhy..51.1079D . дои : 10.1080/00018730110112519 . S2CID 429546 .
- Эрдеш, П .; Реньи, А. (1960). Об эволюции случайных графов (PDF) . Том. 5. Издание Математического института Венгерской академии наук. стр. 17–61.
- Фалуцсос, М.; Фалуцсос, П.; Фалуцсос, К. (1999). «О степенных отношениях топологии Интернета». Комп. Комм. Преподобный . 29 (4): 251–262. дои : 10.1145/316194.316229 .
- Ли, Л.; Олдерсон, Д.; Танака, Р.; Дойл, Дж. К.; Виллинджер, В. (2005). «К теории безмасштабных графов: определение, свойства и последствия (расширенная версия)». arXiv : cond-mat/0501169 .
- Кумар, Р.; Рагхаван, П.; Раджагопалан, С.; Сивакумар, Д.; Томкинс, А.; Упфал, Э. (2000). «Стохастические модели веб-графа» (PDF) . Материалы 41-го ежегодного симпозиума по основам информатики (FOCS) . Редондо-Бич, Калифорния: IEEE CS Press. стр. 57–65.
- Матлис, Январь (4 ноября 2002 г.). «Безмасштабные сети» .
- Ньюман, Марк Э.Дж. (2003). «Структура и функции сложных сетей». Обзор СИАМ . 45 (2): 167–256. arXiv : cond-mat/0303516 . Бибкод : 2003SIAMR..45..167N . дои : 10.1137/S003614450342480 . S2CID 221278130 .
- Пастор-Саторрас Р.; Веспиньяни, А. (2004). Эволюция и структура Интернета: подход статистической физики . Издательство Кембриджского университета. ISBN 0-521-82698-5 .
- Пеннок, DM; Флейк, Г.В.; Лоуренс, С.; Гловер, Э.Дж.; Джайлз, CL (2002). «Победители не получают все: характеристика конкуренции за ссылки в сети» . ПНАС . 99 (8): 5207–11. Бибкод : 2002PNAS...99.5207P . дои : 10.1073/pnas.032085699 . ПМЦ 122747 . ПМИД 16578867 .
- Робб, Джон. Безмасштабные сети и терроризм , 2004.
- Келлер, Э.Ф. (2005). «Возвращаясь к «безмасштабным» сетям» . Биоэссе . 27 (10): 1060–8. doi : 10.1002/bies.20294 . ПМИД 16163729 . Архивировано из оригинала 13 августа 2011 г.
- Оноди, Р.Н.; де Кастро, Пенсильвания (2004). «Комплексное сетевое исследование бразильского футболиста». Физ. Преподобный Е. 70 (3): 037103. arXiv : cond-mat/0409609 . Бибкод : 2004PhRvE..70c7103O . дои : 10.1103/PhysRevE.70.037103 . ПМИД 15524675 . S2CID 31653489 .
- Кастуриратна, Д.; Пиравенан, М. (2015). «Комплексное сетевое исследование бразильского футболиста». наук. Представитель . В Прессе.









































