Периодический граф (кристаллография)

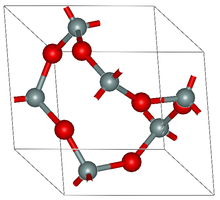
В кристаллографии периодический граф или кристаллическая сеть — это трехмерный периодический граф , то есть трехмерный евклидов граф , вершины или узлы которого являются точками в трехмерном евклидовом пространстве , а ребра (или связи или прокладки) являются отрезками прямых. соединяющие пары вершин, периодические в трех линейно независимых осевых направлениях. Обычно неявно предполагается, что множество вершин равномерно дискретно , т. е. что между любыми двумя вершинами существует фиксированное минимальное расстояние. Вершины могут представлять положения атомов , комплексов или кластеров атомов, таких как ионы отдельных металлов , молекулярные строительные блоки или вторичные строительные единицы , в то время как каждое ребро представляет собой химическую связь или полимерный лиганд .
Хотя понятие периодического графа или кристаллической сети в конечном итоге является математическим (на самом деле кристаллическая сеть — это не что иное, как периодическая реализация абелева графа-накрытия над конечным графом). [1] ) и тесно связан с мозаикой пространства (или сот) в теории многогранников и подобных областях, большая часть современных усилий в этой области мотивирована кристаллической инженерией и предсказанием (проектированием) , включая металлоорганические каркасы . (МОФ) и цеолиты .
История
[ редактировать ]Кристаллическая сеть — это бесконечная молекулярная модель кристалла. Подобные модели существовали в древности , в частности, атомная теория, связанная с Демокритом , которая подвергалась критике со стороны Аристотеля , поскольку такая теория влечет за собой вакуум, который, как считал Аристотель, природа не терпит . Современная атомная теория восходит к Иоганну Кеплеру и его работам по проблемам геометрической упаковки . До двадцатого века графические модели кристаллов фокусировались на положении (атомных) компонентов, и эти модели до двадцатого века были в центре внимания двух противоречий в химии и материаловедении.
Двумя спорами были (1) споры по поводу Роберта Бойля , согласно которой все материальные субстанции состоят из частиц, и (2) споры о том, являются ли кристаллы минералами или каким-то видом растительного явления. корпускулярной теории материи [2] В восемнадцатом веке Кеплер, Николя Стено , Рене Жюст Гаюи и другие постепенно связывали упаковку корпускулярных единиц типа Бойля в массивы с очевидным появлением в результате многогранных структур, напоминающих кристаллы. В течение девятнадцатого века было проведено значительно больше работ по многогранникам , а также по кристаллической структуре , особенно в области вывода кристаллографических групп, основанных на предположении, что кристалл можно рассматривать как регулярный массив элементарных ячеек . В начале двадцатого века физико-химическое сообщество в основном приняло корпускулярную теорию материи Бойля — теперь называемую атомной теорией — и рентгеновская кристаллография использовалась для определения положения атомных или молекулярных компонентов внутри элементарных ячеек (по методу В начале двадцатого века элементарные ячейки считались физически значимыми).
Однако, несмотря на растущее использование молекулярных моделей типа «палка-и-шар» , использование графических краев или отрезков линий для представления химических связей в конкретных кристаллах в последнее время стало популярным, и появились публикации [3] поощрял усилия по определению графических структур известных кристаллов, созданию кристаллических сетей еще неизвестных кристаллов и синтезу кристаллов этих новых кристаллических сетей. Совпадающее расширение интереса к мозаикам и мозаикам , особенно к тем, которые моделируют квазикристаллы , а также развитие современных нанотехнологий , чему способствовал резкий рост вычислительной мощности, позволили разработать алгоритмы из вычислительной геометрии для построения и анализа кристаллических сетей. Тем временем древняя связь между моделями кристаллов и мозаикой расширилась за счет алгебраической топологии . также существует нить интереса В сообществе сверхбольших интеграторов (СБИС) к использованию этих кристаллических сетей в качестве схемотехники. [4]
Базовая формулировка
[ редактировать ]Евклидов граф в трехмерном пространстве — это пара ( V , E ), где V — это набор вершин (иногда называемых точками или узлами), а E — это набор ребер (иногда называемых связями или прокладками), где каждое ребро соединяет два вершины. В полиэдрической и химической литературе существует тенденция называть геометрические графы сетями (в отличие от многогранных сетей ), а номенклатура в химической литературе отличается от номенклатуры теории графов. [5]
Симметрии и периодичность
[ редактировать ]Симметрия изометрия евклидова графа — это основного евклидова пространства, ограничение которого на граф является автоморфизмом ; группа симметрии евклидова графа — это группа его симметрий. Евклидов граф в трехмерном евклидовом пространстве является периодическим, если существуют три линейно независимых перевода , ограничения которых на сеть являются симметриями сети. Часто (и всегда, если мы имеем дело с кристаллической сетью) периодическая сеть имеет конечное число орбит и, таким образом, является равномерно дискретной , поскольку между любыми двумя вершинами существует минимальное расстояние.
В результате получается трехмерный периодический граф как геометрический объект.
Полученная кристаллическая сеть создаст решетку векторов, так что при наличии трех векторов, образующих решетку, эти три вектора будут ограничивать элементарную ячейку , то есть параллелепипед , который, помещенный в любое место в пространстве, будет заключать в себе фрагмент сети, повторяющийся в направления трех осей.
Симметрия и виды вершин и ребер.
[ редактировать ]Две вершины (или ребра) периодического графа симметричны, если они находятся на одной орбите группы симметрии графа; другими словами, две вершины (или ребра) симметричны, если существует симметрия сети, перемещающейся одна на другую. В химии существует тенденция называть орбиты вершин или ребер «разновидностями» вершин или ребер, при этом признавая, что из любых двух вершин или любых двух ребер (одинаково ориентированных) одной и той же орбиты геометрический граф «выглядит одинаковый". Могут использоваться конечные раскраски вершин и ребер (где симметрия должна сохранять раскраску).
Группа симметрии кристаллической сети будет (группой ограничений) кристаллографической пространственной группой , и многие из наиболее распространенных кристаллов имеют очень высокую симметрию, то есть очень мало орбит. Кристаллическая сеть является униодальной, если она имеет одну орбиту вершин (если бы вершины были окрашены и симметрия сохраняла окраску, это потребовало бы, чтобы соответствующий кристалл имел атомы одного элемента или молекулярные строительные блоки одного соединения – но не наоборот, поскольку возможно иметь кристалл одного элемента, но с несколькими орбитами вершин). Кристаллы с одноузловой кристаллической сеткой включают кубический алмаз и некоторые разновидности кристаллов кварца . Униодальность соответствует изогональности в геометрии и вершинной транзитивности в теории графов и дает примеры объективных структур. [6] Кристаллическая сеть является бинодальной, если она имеет две орбиты вершин; кристаллы с бинодальными кристаллическими сетками включают борацит и анатаз . Он транзитивен по ребрам или изотоксичен , если имеет одну орбиту ребер; кристаллы с кристаллической сеткой, переходной по краю, включают борацит, но не анатаз, который имеет две орбиты краев. [7]
Геометрия кристаллических сетей
[ редактировать ]В геометрии кристаллических сетей края можно рассматривать как отрезки линий. Например, в кристаллической сети предполагается, что края не «сталкиваются» в том смысле, что, если рассматривать их как сегменты прямых, они не пересекаются. Из кристаллических сетей можно получить несколько многогранных конструкций. Например, фигура вершины может быть получена путем разделения каждого ребра (рассматриваемого как отрезок прямой) путем вставки точек разделения, а затем фигура вершины данной вершины является выпуклой оболочкой соседних точек разделения (т. е. выпуклой фигурой вершины). многогранник , вершины которого являются соседними точками разделения).
Другая конструкция многогранника заключается в определении окрестности вершины в кристаллической сети. Одним из применений является определение энергетической функции как (возможно, взвешенной) суммы квадратов расстояний от вершин до их соседей, и относительно этой энергетической функции сеть находится в равновесии (относительно этой энергетической функции), если каждая вершина расположен в центре тяжести своей окрестности, [8] это основа программы идентификации Crystal Net SYSTRE. [9] (математики [10] использовать термин «гармонические реализации» вместо «кристаллические сетки в положениях равновесия», поскольку положения характеризуются дискретным уравнением Лапласа; они также ввели понятие стандартных реализаций, которые представляют собой особые гармонические реализации, также характеризующиеся определенным принципом минимальности; см. [11] ). Некоторые кристаллические сети изоморфны кристаллическим сетям в положениях равновесия, и поскольку положение равновесия является нормальной формой , проблема изоморфизма кристаллической сети (т. е. вопрос , изоморфны ли две заданные кристаллические сети как графы; не путать с кристаллическим изоморфизмом ) легко вычисляется, хотя, как часть проблемы изоморфизма графов , в целом он, по-видимому, сложен в вычислительном отношении.
Активные области кристаллического дизайна с использованием кристаллических сеток
[ редактировать ]Предполагается, что [12] что кристаллические сети могут минимизировать энтропию в следующем смысле. Предположим, что вам дан ансамбль равномерно дискретных евклидовых графов, заполняющих пространство, с вершинами, представляющими атомы или молекулярные строительные блоки, а ребра, представляющими связи или лиганды, простирающимися через все пространство, представляющими твердое тело. При некоторых ограничениях может существовать уникальный евклидов граф, который минимизирует разумно определенную энергетическую функцию, и предполагается, что этот евклидов граф обязательно может быть периодическим. Этот вопрос все еще открыт, но некоторые исследователи наблюдают, что кристаллические сети высокой симметрии имеют тенденцию преобладать над наблюдаемыми евклидовыми графиками, полученными из некоторых классов материалов. [13] [14]
Исторически кристаллы создавались путем экспериментов, которые в настоящее время формализованы как комбинаторная химия , но одним из современных требований является синтез материалов, спроектированных заранее, и одно из предложений состоит в том, чтобы спроектировать кристаллы (проекты представляют собой кристаллические сети, возможно, представленные как одна элементарная ячейка кристалла). net), а затем синтезировать их из проекта. [15] Эта попытка, которую Омар Яги назвал ретикулярной химией, ведется по нескольким направлениям: от теоретической [16] синтезу высокопористых кристаллов. [17]
Одной из основных проблем при отжиге кристаллов является контроль составляющих, что может быть затруднительно, если составляющими являются отдельные атомы, например, в цеолитах , которые обычно представляют собой пористые кристаллы, состоящие в основном из кремния и кислорода, а также случайных примесей. Синтез специфического цеолита de novo из новой конструкции кристаллической сетки остается одной из основных целей современных исследований. Аналогичные усилия предпринимаются и в области сульфидов и фосфатов . [ нужна ссылка ]
Контроль становится более управляемым, если компоненты представляют собой молекулярные строительные блоки, т.е. стабильные молекулы, которые можно легко заставить собраться в соответствии с геометрическими ограничениями. [ нужна ссылка ] Обычно, хотя видов составляющих может быть много, существует два основных класса: несколько компактные и часто многогранные вторичные строительные единицы (SBU) и связывающие или соединяющие строительные единицы. Популярным классом примеров являются металлоорганические каркасы (MOF), в которых (классически) вторичными строительными единицами являются ионы металлов или кластеры ионов, а связывающими строительными единицами являются органические лиганды . Эти SBU и лиганды относительно контролируемы, и некоторые новые кристаллы были синтезированы с использованием конструкций новых сетей. [18] Органическим вариантом являются ковалентные органические структуры (COF), в которых SBU могут (но не обязательно) сами по себе быть органическими. [ нужна ссылка ] Больший контроль над SBU и лигандами можно увидеть в том факте, что, хотя новые цеолиты не были синтезированы по каждому проекту, несколько MOF были синтезированы из кристаллических сетей, разработанных для синтеза цеолитов, таких как цеолитоподобные металлоорганические каркасы (Z- МФ) [ нужна ссылка ] и цеолитовый имидазолатный каркас (ZIF).
См. также
[ редактировать ]- Периодические графы как евклидовы графы
- Гипотетический цеолит
- Металлоорганический каркас
- Молекулярный граф
Ссылки
[ редактировать ]- ^ Сунада, Т. (2012), «Лекция по топологической кристаллографии», Япония. Дж. Математика. , 7 : 1–39, doi : 10.1007/s11537-012-1144-4
- ^ Сенешаль, М. (1990), «Краткая история геометрической кристаллографии», в Лима-де-Фариа, Дж. (ред.), Исторический атлас кристаллографии , Kluwer, стр. 43–59.
- ^ Уэллс, А. (1977). Трехмерные сети и многогранники . видеть Коксетер, HSM (июль 1978 г.), «Обзор» , Бюллетень Американского математического общества , 84 (3): 466–470, doi : 10.1090/S0002-9904-1978-14495-4
- ^ Коэн, Э .; Мегиддо, Н. (1991), «Распознавание свойств периодических графов» (PDF) , Серия DIMACS по дискретной математике и теоретической информатике 4: Прикладная геометрия и дискретная математика , Серия DIMACS по дискретной математике и теоретической информатике, 4 : 135– 146, CiteSeerX 10.1.1.124.9538 , doi : 10.1090/dimacs/004/10 , ISBN 9780821865934 , получено 15 августа 2010 г.
- ^ Дельгадо-Фридрихс, О.; О'Киф, М. (2005), «Кристаллические сети как графики: Терминология и определения», Journal of Solid State Chemistry , 178 (8): 2480–2485, Бибкод : 2005JSSCh.178.2480D , doi : 10.1016/j.jssc .2005.06.011
- ^ Джеймс, Р.Д. (2006), «Объективные структуры», Журнал механики и физики твердого тела , 54 (11): 2354–2390, Бибкод : 2006JMPSo..54.2354J , doi : 10.1016/j.jmps.2006.05.008
- ^ «Ресурс ретикулярной химической структуры (RCSR)» .
- ^ Дельгадо-Фридрихс, О.; О'Киф, М. (2003), «Идентификация и расчет симметрии кристаллических сетей» , Acta Crystallogr. А , 59 (4): 351–360, doi : 10.1107/s0108767303012017 , PMID 12832814
- ^ Дельгадо-Фридрихс, О. «СИСТРЕ» . Проект ГАВРОГ.
- ^ Котани, М.; Сунада, Т. (2000), «Стандартные реализации кристаллических решеток с помощью гармонических карт», Trans. Являюсь. Математика. Соц. , 353 : 1–20, doi : 10.1090/S0002-9947-00-02632-5
- ^ Сунада, Т. (2012), Топологическая кристаллография --- С точки зрения дискретного геометрического анализа ---, Обзоры и учебные пособия по прикладным математическим наукам, Vol. 6, Спрингер.
- ^ Радин, К. (1999). Миль плитки . АМС. п. 60.
- ^ О'Киф, М.; Эддауди, М.; Ли, Х.; Рейнеке, Т.; Яги, О.М. (2000), «Основы для расширенных твердых тел: принципы геометрического проектирования», J. Solid State Chem. , 152 (1): 3–20, Бибкод : 2000JSSCh.152....3O , doi : 10.1006/jssc.2000.8723
- ^ Оквиг, Северо-Запад; Дельгадо-Фридрихс, О.; О'Киф, М.; Яги, О.М. (2005), «Ретикулярная химия: возникновение и таксономия сетей и грамматика для проектирования сетей», Acc. хим. Рез. , 38 (3): 176–182, CiteSeerX 10.1.1.590.6758 , doi : 10.1021/ar020022l , PMID 15766236
- ^ Яги, ОМ; О'Киф, М.; Оквиг, Северо-Запад; Чае, Гонконг; Эддауди, М.; Ким, Дж. (2003), «Ретикулярный синтез и дизайн новых материалов» (PDF) , Nature , 423 (12): 705–714, doi : 10.1038/nature01650 , hdl : 2027.42/62718 , PMID 12802325
- ^ Ферей, Жерар (июнь 2000 г.), «Проектирование строительных блоков и химия масштаба», Журнал химии твердого тела , 152 (1): 37–48, Бибкод : 2000JSSCh.152...37F , doi : 10.1006/jssc.2000.8667
- ^ Эддауди, Мохамед; Молер, Дэвид Б.; Ли, Хаилиан; Чен, Банглин; Рейнеке, Тереза М .; О'Киф, Майкл; Яги, Омар М. (2001), «Модульная химия: вторичные строительные блоки как основа для проектирования высокопористых и прочных металлоорганических карбоксилатных каркасов», Acc. хим. Рез. , 34 (4): 319–330, doi : 10.1021/ar000034b , PMID 11308306
- ^ Нуар; Юбанк; Буске; Войтас; Заворотко; Эддауди (2008), «Супермолекулярные строительные блоки (СББ) для проектирования и синтеза высокопористых металлоорганических каркасов», Журнал Американского химического общества , 130 (6): 1833–1835, doi : 10.1021/ja710123s , PMID 18205363
Внешние ссылки
[ редактировать ]- Чампнесс, Северная Каролина (2007). Брага, Э.; Грепиони, Ф. (ред.). Создание рамок координации . Изготовление кристаллов по дизайну: методы, техника и применение. Уайли. стр. 193–207.
- Дельгадо-Фридрихс, О.; Фостер, М.; О'Киф, М.; Прозерпио, Д.; Трейси, М.; Яги, О. (2005). «Что мы знаем о трехпериодических сетях?» (PDF) . Журнал химии твердого тела . 178 (8): 2533–2554. Бибкод : 2005JSSCh.178.2533D . дои : 10.1016/j.jssc.2005.06.037 . Архивировано из оригинала (PDF) 10 июля 2010 г. Проверено 30 сентября 2010 г.
- Хайд, Б.; О'Киф, М. (1996). Кристаллические структуры I: узоры и симметрия .
- Лорд, Э.А.; Маккей, Алабама; Ранганатан, С. (2006). Новая геометрия для новых материалов . Кембриджский университет, Pr.
- Орстрем, Л.; Ларссон, К. (2005). Молекулярные материалы: структурно-сетевой подход . Эльзевир.
- «Атлас перспективных цеолитовых структур» .
- «Проект «Евклидовы шаблоны в неевклидовых мозаиках (EPINET)» .
- «Прогнозирование геометрически ограниченной неорганической структуры [GRINSP]» .
- «Комиссия по математической и теоретической кристаллографии» .
- «Ресурс структур ретикулярной химии [RCSR]» .