Лемма Урысона

В топологии топологическое лемма Урысона — это лемма которая утверждает, что пространство нормально , тогда и только тогда, когда любые два непересекающихся замкнутых подмножества могут быть разделены непрерывной функцией .

Лемма Урысона обычно используется для построения непрерывных функций с различными свойствами в нормальных пространствах. Оно широко применимо, поскольку все пространства и все бикомпакты метрические нормальны. Лемма обобщается (и обычно используется при доказательстве) теоремой о расширении Титце .

Лемма названа в честь математика Павла Самуиловича Урысона .

Обсуждение

Два набора, разделенные кварталами.

Два подмножества $A$ и $B$ пространства топологического $X$ называются разделенными окрестностями, если существуют окрестности $U$ из $A$ и $V$ из $B$ которые не пересекаются. В частности $A$ и $B$ обязательно непересекающиеся.

Два простых подмножества $A$ и $B$ называются разделенными непрерывной функцией, если существует непрерывная функция $f:X\to [0,1]$ от $X$ в единичный интервал $[0,1]$ такой, что $f(a)=0$ для всех $a\in A$ и $f(b)=1$ для всех $b\in B.$ Любая такая функция называется функцией Урысона для $A$ и $B.$ В частности $A$ и $B$ обязательно непересекающиеся.

Отсюда следует, что если два подмножества $A$ и $B$ разделены функцией, то и их замыкания тоже. Также отсюда следует, что если два подмножества $A$ и $B$ разделены функцией, тогда $A$ и $B$ разделены кварталами.

Нормальное пространство — это топологическое пространство, в котором любые два непересекающихся замкнутых множества могут быть разделены окрестностями. Лемма Урысона утверждает, что топологическое пространство нормально тогда и только тогда, когда любые два непересекающихся замкнутых множества можно разделить непрерывной функцией.

Наборы $A$ и $B$ не обязательно должны быть точно разделены $f$, т. е. не обязательно и не гарантируется, что $f(x)\neq 0$ и $\neq 1$ для $x$ снаружи $A$ и $B.$ Топологическое пространство $X$ в котором каждые два непересекающихся замкнутых подмножества $A$ и $B$ точно разделены непрерывной функцией – это совершенно нормально .

Лемма Урысона привела к формулировке других топологических свойств, таких как «тихоновское свойство» и «полностью хаусдорфовы пространства». Например, следствием леммы является то, что нормальные T ₁ пространства являются тихоновскими .

Официальное заявление

Топологическое пространство $X$ нормально тогда и только тогда, когда для любых двух непустых замкнутых непересекающихся подмножеств $A$ и $B$ из $X,$ существует непрерывное отображение $f:X\to [0,1]$ такой, что $f(A)=\{0\}$ и $f(B)=\{1\}.$

Эскиз доказательства

Иллюстрация первых нескольких наборов, построенных в рамках доказательства.

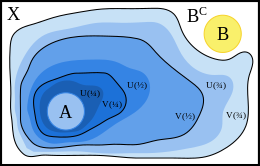
Доказательство продолжается путем многократного применения следующей альтернативной характеристики нормальности. Если $X$ это обычное пространство, $Z$ является открытым подмножеством $X$, и $Y\subseteq Z$ закрыто, то существует открытое $U$ и закрытый $V$ такой, что $Y\subseteq U\subseteq V\subseteq Z$.

Позволять $A$ и $B$ быть непересекающимися замкнутыми подмножествами $X$. Основная идея доказательства состоит в многократном применении этой характеристики нормальности к $A$ и $B^{\complement }$, продолжая создавать новые наборы на каждом этапе.

Наборы, которые мы строим, индексируются двоичными дробями . Для каждой двоичной дроби $r\in (0,1)$, мы строим открытое подмножество $U(r)$ и закрытое подмножество $V(r)$ из $X$ такой, что:

• $A\subseteq U(r)$ и $V(r)\subseteq B^{\complement }$ для всех $r$,
• $U(r)\subseteq V(r)$ для всех $r$,
• Для $r<s$, $V(r)\subseteq U(s)$.

Интуитивно, множества $U(r)$ и $V(r)$ расширяться наружу слоями от $A$:

${\begin{array}{ccccccccccccccc}A&&&&&&&\subseteq &&&&&&&B^{\complement }\\A&&&\subseteq &&&\ U(1/2)&\subseteq &V(1/2)&&&\subseteq &&&B^{\complement }\\A&\subseteq &U(1/4)&\subseteq &V(1/4)&\subseteq &U(1/2)&\subseteq &V(1/2)&\subseteq &U(3/4)&\subseteq &V(3/4)&\subseteq &B^{\complement }\end{array}}$

Это построение осуществляется методом математической индукции . Для базового шага мы определяем два дополнительных набора $U(1)=B^{\complement }$ и $V(0)=A$.

Теперь предположим, что $n\geq 0$ и что наборы $U\left(k/2^{n}\right)$ и $V\left(k/2^{n}\right)$ уже построены для $k\in \{1,\ldots ,2^{n}-1\}$. Заметим, что это пустое выполнение для $n=0$. С $X$ это нормально для любого $a\in \left\{0,1,\ldots ,2^{n}-1\right\}$, мы можем найти открытое и закрытое множество такие, что

$V\left({\frac {a}{2^{n}}}\right)\subseteq U\left({\frac {2a+1}{2^{n+1}}}\right)\subseteq V\left({\frac {2a+1}{2^{n+1}}}\right)\subseteq U\left({\frac {a+1}{2^{n}}}\right)$

Затем проверяются три вышеуказанных условия.

Получив эти наборы, мы определяем $f(x)=1$ если $x\not \in U(r)$ для любого $r$; в противном случае $f(x)=\inf\{r:x\in U(r)\}$ для каждого $x\in X$, где $\inf$ обозначает инфимум . Используя тот факт, что диадические рациональные числа плотны , нетрудно показать, что $f$ непрерывен и обладает свойством $f(A)\subseteq \{0\}$ и $f(B)\subseteq \{1\}.$ Этот шаг требует $V(r)$ наборы для работы.

Проект Mizar полностью формализовал и автоматически проверил доказательство леммы Урысона в файле URYSOHN3 .

См. также

• смягчающий

Ссылки

• Уиллард, Стивен (2004) [1970]. Общая топология . Минеола, Нью-Йорк : Dover Publications . ISBN  978-0-486-43479-7 . OCLC   115240 .
• Уиллард, Стивен (1970). Общая топология . Дуврские публикации. ISBN  0-486-43479-6 .

Внешние ссылки

• «Лемма Урысона» , Математическая энциклопедия , EMS Press , 2001 [1994]
• системы Mizar Доказательство : http://mizar.org/version/current/html/urysohn3.html#T20