метод Горнера

В математике и информатике ( метод Горнера или схема Горнера ) — это алгоритм полиномиальной оценки . Хотя этот метод назван в честь Уильяма Джорджа Хорнера , этот метод намного старше, поскольку сам Хорнер приписал его Жозефу-Луи Лагранжу , и его можно проследить на многие сотни лет назад у китайских и персидских математиков. После появления компьютеров этот алгоритм стал фундаментальным для эффективных вычислений с полиномами.

Алгоритм основан на правиле Горнера , в котором многочлен записывается во вложенной форме :

$${\begin{aligned}&a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\={}&a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}.\end{aligned}}$$

Это позволяет оценить полином степени n только с помощью $n$ умножения и $n$ дополнения. Это оптимально, поскольку существуют полиномы степени n , которые невозможно вычислить с помощью меньшего количества арифметических операций.

Альтернативно, метод Хорнера также относится к методу аппроксимации корней многочленов, описанному Хорнером в 1819 году. Это вариант метода Ньютона-Рафсона, который стал более эффективным для ручных вычислений за счет применения правила Горнера. Он широко использовался до тех пор, пока компьютеры не стали широко использоваться примерно в 1970 году.

Полиномиальная оценка и деление в столбик

Учитывая полином

$$p(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n},$$

где $a_{0},\ldots ,a_{n}$ являются постоянными коэффициентами, проблема состоит в том, чтобы оценить полином при определенном значении $x_{0}$ из $x.$

Для этого новая последовательность констант определяется рекурсивно следующим образом:

$${\begin{aligned}b_{n}&:=a_{n}\\b_{n-1}&:=a_{n-1}+b_{n}x_{0}\\&~~~\vdots \\b_{1}&:=a_{1}+b_{2}x_{0}\\b_{0}&:=a_{0}+b_{1}x_{0}.\end{aligned}}$$

( 1 )

Затем $b_{0}$ это ценность $p(x_{0})$.

Чтобы понять, почему это работает, полином можно записать в виде

$$p(x)=a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}\ .$$

Таким образом, итеративно заменяя $b_{i}$ в выражение,

$${\begin{aligned}p(x_{0})&=a_{0}+x_{0}{\Big (}a_{1}+x_{0}{\big (}a_{2}+\cdots +x_{0}(a_{n-1}+b_{n}x_{0})\cdots {\big )}{\Big )}\\&=a_{0}+x_{0}{\Big (}a_{1}+x_{0}{\big (}a_{2}+\cdots +x_{0}b_{n-1}{\big )}{\Big )}\\&~~\vdots \\&=a_{0}+x_{0}b_{1}\\&=b_{0}.\end{aligned}}$$

Теперь это можно доказать;

$$p(x)=\left(b_{1}+b_{2}x+b_{3}x^{2}+b_{4}x^{3}+\cdots +b_{n-1}x^{n-2}+b_{n}x^{n-1}\right)\left(x-x_{0}\right)+b_{0}$$

( 2 )

Это выражение представляет собой практическое применение Хорнера, поскольку оно предлагает очень быстрый способ определения результата;

$$p(x)/(x-x_{0})$$

с $b_{0}$ (что равно $p(x_{0})$), являющийся остатком от деления, как показано в примерах ниже. Если $x_{0}$ является корнем $p(x)$, затем $b_{0}=0$ (это означает, что остаток $0$), что означает, что вы можете учитывать $p(x)$ как $x-x_{0}$.

Чтобы найти последовательные $b$-ценности, вы начинаете с определения $b_{n}$, что просто равно $a_{n}$. Затем вы работаете рекурсивно, используя формулу:

$$b_{n-1}=a_{n-1}+b_{n}x_{0}$$

пока ты не прибудешь в $b_{0}$.

Примеры

Оценивать $f(x)=2x^{3}-6x^{2}+2x-1$ для $x=3$.

Мы используем синтетическое деление следующим образом:

 x0│   x3    x2    x1    x0
 3 │   2    −6     2    −1
   │         6     0     6
   └────────────────────────
       2     0     2     5

Записи в третьей строке представляют собой сумму записей в первых двух. Каждая запись во второй строке представляет собой произведение значения x ( в данном примере 3 ) на запись третьей строки слева. Записи в первой строке представляют собой коэффициенты оцениваемого многочлена. Тогда остаток $f(x)$ при делении на $x-3$ это 5 .

Но по теореме о полиномиальном остатке мы знаем, что остаток равен $f(3)$. Таким образом, $f(3)=5$.

В этом примере, если $a_{3}=2,a_{2}=-6,a_{1}=2,a_{0}=-1$ мы можем это видеть $b_{3}=2,b_{2}=0,b_{1}=2,b_{0}=5$, записи в третьей строке. Итак, синтетическое деление (которое на самом деле было изобретено и опубликовано Руффини за 10 лет до публикации Хорнера) проще в использовании; Можно показать, что он эквивалентен методу Горнера.

Как следствие полиномиальной теоремы об остатках, элементы в третьей строке представляют собой коэффициенты многочлена второй степени, частное $f(x)$ при делении на $x-3$. Остаток 5 . Это делает метод Горнера полезным для деления полинома в длину .

Разделять $x^{3}-6x^{2}+11x-6$ к $x-2$:

 2 │   1    −6    11    −6
   │         2    −8     6
   └────────────────────────
       1    −4     3     0

Фактор $x^{2}-4x+3$.

Позволять $f_{1}(x)=4x^{4}-6x^{3}+3x-5$ и $f_{2}(x)=2x-1$. Разделять $f_{1}(x)$ к $f_{2}\,(x)$ используя метод Горнера.

  0.5 │ 4  −6   0   3  −5
      │     2  −2  −1   1
      └───────────────────────
        2  −2  −1   1  −4

Третья строка представляет собой сумму первых двух строк, разделенную на 2 . Каждая запись во второй строке представляет собой произведение 1 на запись третьей строки слева. Ответ:

$${\frac {f_{1}(x)}{f_{2}(x)}}=2x^{3}-2x^{2}-x+1-{\frac {4}{2x-1}}.$$

Эффективность

Оценка с использованием мономиальной формы степени $n$ полином требует не более $n$ дополнения и $(n^{2}+n)/2$ умножения, если степени вычисляются путем многократного умножения и каждый моном оценивается индивидуально. Стоимость может быть снижена до $n$ дополнения и $2n-1$ умножения, оценивая степени $x$ путем итерации.

Если числовые данные представлены в виде цифр (или битов), то наивный алгоритм также предполагает хранение приблизительно $2n$ раз количество битов $x$: оцененный полином имеет приблизительную величину $x^{n}$, и нужно также хранить $x^{n}$ сам. Напротив, метод Горнера требует только $n$ дополнения и $n$ умножения, и его требования к хранению составляют только $n$ раз количество битов $x$. Альтернативно, метод Хорнера можно вычислить с помощью $n$ слитое умножение – сложение . Метод Горнера также можно расширить для оценки первого $k$ производные многочлена с $kn$ сложения и умножения.

Метод Хорнера оптимален в том смысле, что любой алгоритм вычисления произвольного полинома должен использовать как минимум столько же операций. Александр Островский доказал в 1954 году, что количество необходимых дополнений минимально. Виктор Пан доказал в 1966 году, что число умножений минимально. Однако, когда $x$ является матрицей, метод Горнера не является оптимальным .

Это предполагает, что полином оценивается в мономиальной форме и никакое предварительное обусловливание представления не допускается, что имеет смысл, если полином оценивается только один раз. Однако если разрешено предварительное условие и полином необходимо вычислять много раз, то возможны более быстрые алгоритмы . Они включают в себя преобразование представления многочлена. В общем, степень- $n$ полином можно вычислить, используя только ⌊ n /2 ⌋ +2 умножения и $n$ дополнения.

Параллельная оценка

См. также: Схема Эстрина.

Недостатком правила Горнера является то, что все операции являются последовательно зависимыми , поэтому на современных компьютерах невозможно воспользоваться преимуществами параллелизма на уровне команд . В большинстве приложений, где важна эффективность оценки полиномов, множество полиномов низкого порядка оцениваются одновременно (для каждого пикселя или многоугольника в компьютерной графике или для каждого квадрата сетки в численном моделировании), поэтому нет необходимости находить параллелизм внутри одиночная полиномиальная оценка.

Однако если оценивается один полином очень высокого порядка, может быть полезно разбить его следующим образом:

$${\begin{aligned}p(x)&=\sum _{i=0}^{n}a_{i}x^{i}\\[1ex]&=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\[1ex]&=\left(a_{0}+a_{2}x^{2}+a_{4}x^{4}+\cdots \right)+\left(a_{1}x+a_{3}x^{3}+a_{5}x^{5}+\cdots \right)\\[1ex]&=\left(a_{0}+a_{2}x^{2}+a_{4}x^{4}+\cdots \right)+x\left(a_{1}+a_{3}x^{2}+a_{5}x^{4}+\cdots \right)\\[1ex]&=\sum _{i=0}^{\lfloor n/2\rfloor }a_{2i}x^{2i}+x\sum _{i=0}^{\lfloor n/2\rfloor }a_{2i+1}x^{2i}\\[1ex]&=p_{0}(x^{2})+xp_{1}(x^{2}).\end{aligned}}$$

В более общем смысле суммирование можно разбить на k частей:

$$p(x)=\sum _{i=0}^{n}a_{i}x^{i}=\sum _{j=0}^{k-1}x^{j}\sum _{i=0}^{\lfloor n/k\rfloor }a_{ki+j}x^{ki}=\sum _{j=0}^{k-1}x^{j}p_{j}(x^{k})$$

где внутренние суммирования могут быть оценены с использованием отдельных параллельных экземпляров метода Хорнера. Это требует немного больше операций, чем базовый метод Хорнера, но позволяет k -way SIMD выполнять большинство из них . Современные компиляторы обычно оценивают полиномы таким образом, когда это выгодно, хотя для вычислений с плавающей запятой это требует включения (небезопасной) реассоциативной математики. .

Приложение к умножению и делению чисел с плавающей запятой

Основная статья: алгоритм умножения § Сдвиг и сложение

Метод Хорнера — это быстрый, эффективный с точки зрения кода метод умножения и деления двоичных чисел на микроконтроллере без аппаратного умножителя . Одно из двоичных чисел, подлежащих умножению, представляется в виде тривиального многочлена, где (используя приведенные выше обозначения) $a_{i}=1$, и $x=2$. Затем x (или x в некоторой степени) многократно вычитается. В этой двоичной системе счисления (основание 2) $x=2$, поэтому степени 2 многократно вычитаются.

Пример

Например, чтобы найти произведение двух чисел (0,15625) и m :

$${\begin{aligned}(0.15625)m&=(0.00101_{b})m=\left(2^{-3}+2^{-5}\right)m=\left(2^{-3})m+(2^{-5}\right)m\\&=2^{-3}\left(m+\left(2^{-2}\right)m\right)=2^{-3}\left(m+2^{-2}(m)\right).\end{aligned}}$$

Метод

Чтобы найти произведение двух двоичных чисел d и m :

1. Регистр, содержащий промежуточный результат, инициализируется значением d .
2. Начните с младшего (крайнего правого) ненулевого бита в m .
   2. Подсчитайте (слева) количество битовых позиций до следующего по значимости ненулевого бита. Если более значимых битов нет, то берем значение текущей битовой позиции.
   3. Используя это значение, выполните операцию сдвига влево на это количество бит в регистре, содержащем промежуточный результат.
3. Если все ненулевые биты были подсчитаны, то в регистре промежуточного результата теперь хранится окончательный результат. В противном случае добавьте d к промежуточному результату и перейдите к шагу 2 со следующим старшим битом m .

Вывод

В общем, для двоичного числа с битовыми значениями ( $d_{3}d_{2}d_{1}d_{0}$) продукт

$$(d_{3}2^{3}+d_{2}2^{2}+d_{1}2^{1}+d_{0}2^{0})m=d_{3}2^{3}m+d_{2}2^{2}m+d_{1}2^{1}m+d_{0}2^{0}m.$$

На этом этапе алгоритма требуется, чтобы члены с нулевыми коэффициентами отбрасывались, чтобы учитывались только двоичные коэффициенты, равные единице, таким образом, проблема умножения или деления на ноль не является проблемой, несмотря на это следствие в алгоритме. факторизованное уравнение:

$$=d_{0}\left(m+2{\frac {d_{1}}{d_{0}}}\left(m+2{\frac {d_{2}}{d_{1}}}\left(m+2{\frac {d_{3}}{d_{2}}}(m)\right)\right)\right).$$

Все знаменатели равны единице (или член отсутствует), поэтому это сводится к

$$=d_{0}(m+2{d_{1}}(m+2{d_{2}}(m+2{d_{3}}(m)))),$$

или эквивалентно (в соответствии с «методом», описанным выше)

$$=d_{3}(m+2^{-1}{d_{2}}(m+2^{-1}{d_{1}}(m+{d_{0}}(m)))).$$

В двоичной математике (с основанием 2) умножение на степень 2 — это просто операция сдвига регистра . Таким образом, умножение на 2 вычисляется в системе счисления по основанию 2 путем арифметического сдвига . Фактор (2 ⁻¹ вправо ) — арифметический сдвиг , a (0) не приводит к выполнению операции (поскольку 2 ⁰ = 1 – мультипликативный единичный элемент ), а a (2 ¹ ) приводит к арифметическому сдвигу влево. Произведение умножения теперь можно быстро вычислить, используя только арифметические операции сдвига, сложения и вычитания.

Этот метод особенно быстр на процессорах, поддерживающих операцию сдвига и сложения с одной командой. По сравнению с библиотекой чисел с плавающей запятой C, метод Хорнера жертвует некоторой точностью, однако номинально он работает в 13 раз быстрее (в 16 раз быстрее, когда используется форма « канонической знаковой цифры » (CSD)) и использует только 20% пространства кода.

Другие приложения

Метод Хорнера можно использовать для преобразования между различными позиционными системами счисления - в этом случае x является основанием системы счисления, а коэффициенты a _i - это цифры представления по основанию x данного числа - а также может использоваться, если x — матрица , и в этом случае выигрыш в вычислительной эффективности еще больше. Однако для таких случаев более быстрые методы . известны

Поиск корня полинома

Используя алгоритм деления в столбик в сочетании с методом Ньютона , можно аппроксимировать действительные корни многочлена. Алгоритм работает следующим образом. Учитывая полином $p_{n}(x)$ степени $n$ с нулями $z_{n}<z_{n-1}<\cdots <z_{1},$ сделать первоначальное предположение $x_{0}$ такой, что $z_{1}<x_{0}$. Теперь повторите следующие два шага:

1. Используя метод Ньютона , найдите наибольший ноль $z_{1}$ из $p_{n}(x)$ используя предположение $x_{0}$.
2. Используя метод Горнера, разделите $(x-z_{1})$ чтобы получить $p_{n-1}$. Вернитесь к шагу 1, но используйте полином $p_{n-1}$ и первоначальное предположение $z_{1}$.

Эти два шага повторяются до тех пор, пока для многочлена не будут найдены все действительные нули. Если аппроксимированные нули недостаточно точны, полученные значения можно использовать в качестве начальных предположений для метода Ньютона, но с использованием полного полинома, а не уменьшенных полиномов.

Пример

Поиск корня полинома с использованием метода Горнера

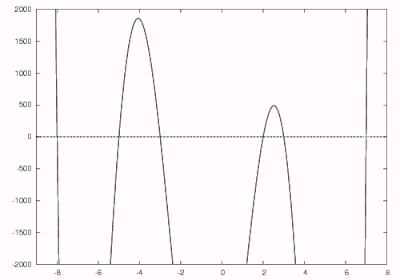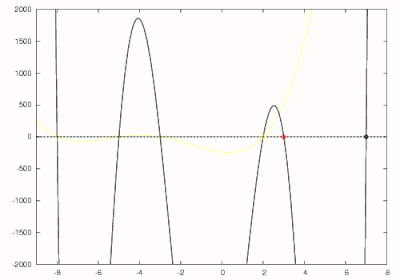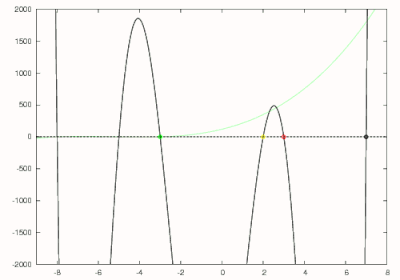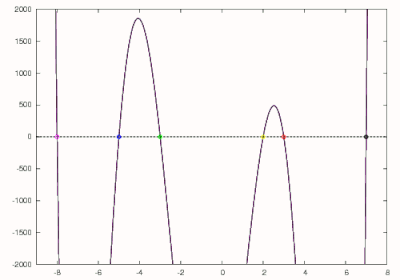
Рассмотрим полином

$$p_{6}(x)=(x+8)(x+5)(x+3)(x-2)(x-3)(x-7)$$

который можно расширить до

$$p_{6}(x)=x^{6}+4x^{5}-72x^{4}-214x^{3}+1127x^{2}+1602x-5040.$$

Из вышесказанного мы знаем, что наибольший корень этого многочлена равен 7, поэтому мы можем сделать первоначальное предположение, равное 8. Используя метод Ньютона, первый ноль числа 7 находится, как показано черным на рисунке справа. Следующий $p(x)$ делится на $(x-7)$ чтобы получить

$$p_{5}(x)=x^{5}+11x^{4}+5x^{3}-179x^{2}-126x+720$$

который на рисунке справа нарисован красным. Метод Ньютона используется для поиска наибольшего нуля этого многочлена с начальной догадкой 7. Самый большой нуль этого многочлена, который соответствует второму по величине нулю исходного многочлена, находится в позиции 3 и обведен красным. Полином 5-й степени теперь делится на $(x-3)$ чтобы получить

$$p_{4}(x)=x^{4}+14x^{3}+47x^{2}-38x-240$$

который показан желтым цветом. Ноль для этого полинома снова находится в точке 2 с использованием метода Ньютона и обведен желтым кружком. Метод Горнера теперь используется для получения

$$p_{3}(x)=x^{3}+16x^{2}+79x+120$$

который показан зеленым цветом и имеет ноль при -3. Этот многочлен далее сводится к

$$p_{2}(x)=x^{2}+13x+40$$

который показан синим цветом и дает ноль -5. Конечный корень исходного полинома можно найти либо используя последний ноль в качестве первоначального предположения для метода Ньютона, либо путем сокращения $p_{2}(x)$ и решение линейного уравнения . Как можно видеть, ожидаемые корни -8, -5, -3, 2, 3 и 7 были найдены.

Деленная разность многочлена

Метод Горнера можно модифицировать для вычисления разделенной разности. $(p(y)-p(x))/(y-x).$ Учитывая полином (как и раньше)

$$p(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n},$$

действуйте следующим образом

$${\begin{aligned}b_{n}&=a_{n},&\quad d_{n}&=b_{n},\\b_{n-1}&=a_{n-1}+b_{n}x,&\quad d_{n-1}&=b_{n-1}+d_{n}y,\\&{}\ \ \vdots &\quad &{}\ \ \vdots \\b_{1}&=a_{1}+b_{2}x,&\quad d_{1}&=b_{1}+d_{2}y,\\b_{0}&=a_{0}+b_{1}x.\end{aligned}}$$

По завершении мы имеем

$${\begin{aligned}p(x)&=b_{0},\\{\frac {p(y)-p(x)}{y-x}}&=d_{1},\\p(y)&=b_{0}+(y-x)d_{1}.\end{aligned}}$$

Это вычисление разделенной разности подвержено меньшей ошибке округления, чем вычисление $p(x)$ и $p(y)$ отдельно, особенно когда $x\approx y$. Замена $y=x$ в этом методе дает $d_{1}=p'(x)$, производная от $p(x)$.

История

Алгоритм Цинь Цзюшао для решения квадратного полиномиального уравнения $-x^{4}+763200x^{2}-40642560000=0$
результат: х =840

Статья Хорнера под названием «Новый метод решения числовых уравнений всех порядков методом непрерывной аппроксимации» был прочитан перед Лондонским королевским обществом на его заседании 1 июля 1819 года с продолжением в 1823 году. Статья Хорнера во второй части «Философских трудов Лондонского королевского общества» за 1819 год была тепло и широко встречена рецензентом . в номере «Ежемесячного обзора: или Литературного журнала» за апрель 1820 г.; для сравнения, техническая статья Чарльза Бэббиджа в этом обзоре категорически отвергается. В серии обзоров в «Ежемесячном обзоре» за сентябрь 1821 года делается вывод, что Холдред был первым человеком, открывшим прямое и общее практическое решение числовых уравнений. Фуллер показал, что метод, описанный в статье Горнера 1819 года, отличается от того, что впоследствии стало известно как «метод Горнера», и что, следовательно, приоритет этого метода должен принадлежать Холдреду (1820).

В отличие от своих английских современников, Хорнер опирался на континентальную литературу, особенно на произведения Арбогаста . Известно также, что Хорнер внимательно прочитал книгу Джона Бонникасла по алгебре, хотя и пренебрег работами Паоло Руффини .

Хотя Хорнеру приписывают создание этого метода доступным и практичным, он был известен задолго до Хорнера. В обратном хронологическом порядке метод Горнера уже был известен:

• Паоло Руффини в 1809 году (см. правило Руффини )
• Исаак Ньютон в 1669 году.
• китайский математик Чжу Шицзе в 14 веке.
• китайский математик Цинь Цзюшао в своем «Математическом трактате в девяти разделах» XIII века.
• персидский в математик Шараф ад-Дин аль-Туси XII веке (первый, кто применил этот метод в общем случае кубического уравнения)
• китайский математик Цзя Сянь в 11 веке ( династия Сун )
• «Девять глав математического искусства» , китайская работа династии Хань (202 г. до н.э. – 220 г. н.э.) под редакцией Лю Хуэя (ок. III век).

Цинь Цзюшао в своем «Шу Шу Цзю Чжан» ( «Математический трактат в девяти разделах» ; 1247) представляет портфель методов типа Горнера для решения полиномиальных уравнений, который был основан на более ранних работах математика Цзя Сяня из династии Сун XI века ; например, один метод специально подходит для би-квинтик, пример которого приводит Цинь, в соответствии с тогдашней китайской традицией изучения конкретных случаев. Ёсио Миками в книге «Развитие математики в Китае и Японии» (Лейпциг, 1913 г.) писал:

«...кто может отрицать тот факт, что выдающийся процесс Горнера был использован в Китае, по крайней мере, почти на шесть долгих веков раньше, чем в Европе... Мы, конечно, никоим образом не намерены приписывать изобретение Горнера китайскому происхождению, но по прошествии времени вполне возможно, что европейцы могли знать о китайском методе прямым или косвенным образом».

Ульрих Либбрехт заключил: «Очевидно, что эта процедура — китайское изобретение… этот метод не был известен в Индии» . Он сказал, что Фибоначчи, вероятно, узнал об этом от арабов, которые, возможно, позаимствовали у китайцев. Извлечение квадратных и кубических корней аналогичным образом уже обсуждалось Лю Хуэем в связи с задачами IV.16 и 22 в «Цзю Чжан Суань Шу» , тогда как Ван Сяотун в VII веке предполагал, что его читатели могут решать кубики с помощью метода аппроксимации, описанного в его книга Цзигу Суаньцзин .

См. также

• Алгоритм Кленшоу для вычисления полиномов в форме Чебышева
• Алгоритм Де Бура для оценки сплайнов в B-сплайна форме
• Алгоритм Де Кастельжо для оценки полиномов в форме Безье
• Схема Эстрина для облегчения распараллеливания на современных компьютерных архитектурах
• Метод Лилля для графического приближения корней
• Правило Руффини и синтетическое деление для деления многочлена на бином формы x - r

Ссылки

• Берггрен, Дж. Л. (1990). «Инновации и традиции в Муадалате Шарафа ад-Дина ат-Туси». Журнал Американского восточного общества . 110 (2): 304–309. дои : 10.2307/604533 . JSTOR   604533 .
• Каджори, Флориан (1911). «Метод аппроксимации Горнера, предсказанный Руффини» . Бюллетень Американского математического общества . 17 (8): 409–414. дои : 10.1090/s0002-9904-1911-02072-9 . Архивировано из оригинала 4 сентября 2017 г. Проверено 4 марта 2012 г. Прочтите перед Юго-западной секцией Американского математического общества 26 ноября 1910 года.
• Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн 10.1016/0315-0860(81)90069-0, Клиффорд (2009). «Введение в алгоритмы» . История Математики . 8 (3) (3-е изд.). Массачусетский технологический институт Пресс: 277–318. дои : 10.1016/0315-0860(81)90069-0 . {{cite journal}}: CS1 maint: числовые имена: список авторов ( ссылка )
• Фейтман, Р.Дж .; Кахан, В. (2000). Улучшение точных интегралов из систем символьной алгебры (PDF) (Отчет). ПАМ. Калифорнийский университет в Беркли: Центр чистой и прикладной математики. Архивировано из оригинала (PDF) 14 августа 2017 г. Проверено 17 мая 2018 г.
• Фуллер, AT (1999). «Хорнер против Холдреда: эпизод в истории корневых вычислений» . История Математики . 26 : 29–51. дои : 10.1006/hmat.1998.2214 .
• Хайэм, Николас (2002). Точность и устойчивость численных алгоритмов . СИАМ. ISBN  978-0-89871-521-7 .
• Холдред, Т. (1820). Новый метод решения уравнений с легкостью и скоростью; с помощью которого находится истинное значение неизвестной величины без предварительного уменьшения. С дополнением, содержащим два других метода решения уравнений, основанных на том же принципе (PDF) . Ричард Уоттс. Архивировано из оригинала (PDF) 6 января 2014 г. Проверено 10 декабря 2012 г.

  Метод Холдреда находится в приложении на следующей странице под номером 45 (52-я страница PDF-версии).

• Хорнер, Уильям Джордж (июль 1819 г.). «Новый метод решения численных уравнений всех порядков методом непрерывной аппроксимации». Философские труды . 109 . Лондонское королевское общество: 308–335. дои : 10.1098/rstl.1819.0023 . JSTOR   107508 . S2CID   186210512 .

  Доступен напрямую в Интернете по ссылке, но также перепечатан с оценкой в ​​DE Smith: A Source Book in Mathematics , McGraw-Hill, 1929; Перепечатка Дувра, 2 тома, 1959 г.

• Кнут, Дональд (1997). Искусство компьютерного программирования . Том. 2: Получисловые алгоритмы (3-е изд.). Аддисон-Уэсли. стр. 486–488 в разделе 4.6.4. ISBN  978-0-201-89684-8 .
• Кресс, Райнер (1991). Численный анализ . Спрингер.
• Крипасагар, Венкат (март 2008 г.). «Эффективная микроматематика - методы умножения и деления для микроконтроллеров». Журнал Circuit Cellar (212).
• Либбрехт, Ульрих (2005). «Глава 13» . Китайская математика в тринадцатом веке (2-е изд.). Дувр. ISBN  978-0-486-44619-6 . Архивировано из оригинала 6 июня 2017 г. Проверено 23 августа 2016 г.
• Миками, Ёсио (1913). «Глава 11. Цинь Цзю-Шао» . Развитие математики в Китае и Японии (1-е изд.). Переиздание Chelsea Publishing Co. стр. 74–77.
• Островский, Александр М. (1954). «О двух задачах абстрактной алгебры, связанных с правилом Горнера» . Исследования по математике и механике, представленные Рихарду фон Мизесу . Академическая пресса. стр. 40–48. ISBN  978-1-4832-3272-0 . Архивировано из оригинала 15 апреля 2019 г. Проверено 23 августа 2016 г.
• Пан, Ю. Джа (1966). «О средствах вычисления значений полиномов». Русская математика. Опросы . 21 : 105–136. дои : 10.1070/rm1966v021n01abeh004147 . S2CID   250869179 .
• Панкевич, В. (1968). «Алгоритм 337: вычисление значений полинома и его производных по схеме Горнера» . Коммуникации АКМ . 11 (9). ACM: 633. дои : 10.1145/364063.364089 . S2CID   52859619 .
• Шпигель, Мюррей Р. (1956). Очерк теории и проблем студенческой алгебры Шаума . МакГроу-Хилл. ISBN  9780070602267 .
• Темпл, Роберт (1986). Гений Китая: 3000 лет науки, открытий и изобретений . Саймон и Шустер. ISBN  978-0-671-62028-8 .
• Уиттакер, ET ; Робинсон, Г. (1924). Исчисление наблюдений . Лондон: Блэки.
• Уайли, Александр (1897). «Заметки о науке китайской арифметики» . Китайские исследования . Шанхай. стр. 159–194. {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

  Перепечатано из номеров The North China Herald (1852 г.).

Внешние ссылки

• «Схема Хорнера» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Цю Цзинь-Шао, Шу Шу Цзю Чжан (изд. Цун Шу Цзи Чэн)
• Дополнительную информацию о приложении для поиска корней см. в [1]. Архивировано 28 сентября 2018 г. на Wayback Machine.