Цепь Маркова с непрерывным временем

Эта статья о математических свойствах цепей Маркова с непрерывным временем. Для общей области исследования см. Цепь Маркова .

Цепь Маркова с непрерывным временем ( CTMC ) — это непрерывный стохастический процесс , в котором для каждого состояния процесс меняет состояние в соответствии с экспоненциальной случайной величиной , а затем переходит в другое состояние, определенное вероятностями стохастической матрицы . Эквивалентная формулировка описывает процесс как изменение состояния в соответствии с наименьшим значением набора экспоненциальных случайных величин, по одной для каждого возможного состояния, в которое он может перейти, с параметрами, определяемыми текущим состоянием.

Пример CTMC с тремя состояниями $\{0,1,2\}$ заключается в следующем: процесс совершает переход через время, заданное временем удержания — экспоненциальной случайной величиной $E_{i}$, где i — его текущее состояние. Каждая случайная величина независима и такова, что $E_{0}\sim {\text{Exp}}(6)$, $E_{1}\sim {\text{Exp}}(12)$ и $E_{2}\sim {\text{Exp}}(18)$. Когда необходимо совершить переход, процесс движется по цепочке скачков — цепи Маркова с дискретным временем и стохастической матрицей:

${\begin{bmatrix}0&{\frac {1}{2}}&{\frac {1}{2}}\\{\frac {1}{3}}&0&{\frac {2}{3}}\\{\frac {5}{6}}&{\frac {1}{6}}&0\end{bmatrix}}.$

Эквивалентно, по свойству конкурирующих экспонент , этот CTMC меняет состояние из состояния i в соответствии с минимумом двух случайных величин, которые являются независимыми и такими, что $E_{i,j}\sim {\text{Exp}}(q_{i,j})$ для $i\neq j$ где параметры заданы Q-матрицей $Q=(q_{i,j})$

${\begin{bmatrix}-6&3&3\\4&-12&8\\15&3&-18\end{bmatrix}}.$

Каждая недиагональная запись $q_{i,j}$ может быть вычислена как вероятность того, что цепочка переходов перейдет из состояния i в состояние j , деленная на ожидаемое время удержания состояния i . Диагональные элементы выбираются так, чтобы сумма каждой строки была равна 0.

CTMC удовлетворяет свойству Маркова , согласно которому его поведение зависит только от его текущего состояния, а не от его прошлого поведения, из-за отсутствия памяти экспоненциального распределения и цепей Маркова с дискретным временем.

Определение

Позволять $(\Omega ,{\cal {A}},\Pr )$ — вероятностное пространство, пусть $S$ — счетное непустое множество, и пусть $T=\mathbb {R} _{\geq 0}$ ( $T$ «время»). Оборудовать $S$ с дискретной метрикой , так что мы можем понять непрерывность справа функций $\mathbb {R} _{\geq 0}\to S$. Цепь Маркова с непрерывным временем определяется следующим образом:

• Вектор вероятности $\lambda$ на $S$ (которое ниже мы будем интерпретировать как начальное распределение цепи Маркова), и
• Матрица ставок $Q$ на $S$, то есть функция $Q:S^{2}\to \mathbb {R}$ такой, что

1. для всех отдельных $i,j\in S,0\leq q_{i,j}$,
2. для всех $i\in S,$ $\sum _{j\in I:j\neq i}q_{i,j}=-q_{i,i}.$ (Даже если $I$ бесконечна, эта сумма априори корректна (возможно, равна $+\infty$), поскольку каждое слагаемое суммы неотрицательно. Апостериори мы знаем, что сумма также должна быть конечной (не равной $+\infty$), поскольку мы предполагаем, что оно равно $-q_{i,i}$ и мы предположили $Q$ действительно ценится. Некоторые авторы вместо этого используют определение, которое дословно одинаково, за исключением измененного условия. $Q:S^{2}\to \mathbb {R} \cup \{-\infty \}$и сказать $Q$ является стабильным или полностью стабильным , что означает $\operatorname {range} Q\subseteq \mathbb {R}$, т. е. каждая запись имеет действительное значение.)

Обратите внимание, что суммы строк $Q$ 0: $\forall i\in S~\sum _{j\in I}q_{i,j}=0,$ или более кратко, $Q\cdot 1=0$. Эта ситуация контрастирует с ситуацией для цепей Маркова с дискретным временем , где все суммы строк матрицы перехода равны единице.

Теперь позвольте $X:T\to S^{\Omega }$ такой, что $\forall t\in T~X(t)$ является $({\cal {A}},{\cal {P}}(S))$-измеримый. Существует три эквивалентных способа определения $X$ будучи Марковым с начальным распределением $\lambda$ и матрица ставок $Q$: через вероятности перехода или через цепочку переходов и время удержания.

В качестве прелюдии к определению вероятности перехода мы сначала мотивируем определение регулярной матрицы ставок . Мы будем использовать матрицу скорости перехода $Q$ задать динамику цепи Маркова путем создания набора матриц перехода $P(t)$ на $S$ ( $t\in \mathbb {R} _{\geq 0}$), по следующей теореме.

Теорема: Существование решения обратных уравнений Колмогорова . — Существует $P\in ([0,1]^{S\times S})^{T}$ такой, что для всех $i,j\in S$ запись $(P(t)_{i,j})_{t\in T}$ является дифференцируемым и $P$ удовлетворяет обратным уравнениям Колмогорова :

$$P(0)=([i=j])_{i,j\in S},~\forall t\in T~\forall i,j\in S~~(P(t)_{i,j})'=\sum _{k\in S}q_{i,k}P(t)_{k,j}.$$

( 0 )

Мы говорим $Q$ является регулярным , что означает, что для указанной выше системы действительно существует единственность, т. е. существует ровно одно решение. Мы говорим $Q$ нерегулярно , значит $Q$ не является регулярным. Если $S$ конечно, то существует ровно одно решение, а именно $P=(e^{tQ})_{t\in T},$ и, следовательно, $Q$ является регулярным. В противном случае, $S$ бесконечно, и существуют нерегулярные матрицы скорости перехода на $S$. Если $Q$ регулярно, то для единственного решения $P$, для каждого $t\in T$, $P(t)$ будет стохастическая матрица . Мы будем считать $Q$ является регулярным с начала следующего подраздела до конца этого раздела, хотя и является обычным чтобы не включать это предположение. (Примечание для эксперта: таким образом, мы не определяем цепи Маркова с непрерывным временем вообще, а только невзрывные цепи Маркова с непрерывным временем.)

перехода

Позволять $P$ быть (единственным) решением системы ( 0 ). (Единственность гарантируется нашим предположением, что $Q$ является регулярным.) Мы говорим $X$ является марковским с начальным распределением $\lambda$ и матрица ставок $Q$ означает: для любого неотрицательного целого числа $n\geq 0$, для всех $t_{0},\dots ,t_{n+1}\in T$ такой, что $t_{0}<\dots <t_{n+1},$ для всех $i_{0},\dots ,i_{n+1}\in I,$

$\Pr(X_{0}=i_{0},\dots ,X_{t_{n+1}}=i_{n+1})=\lambda _{i_{0}}\prod _{k\in \mathbb {Z} :0\leq k\leq n}P(t_{k+1}-t_{k})_{i_{k},i_{k+1}}$. ( 1 )

Используя индукцию и тот факт, что $\forall A,B\in {\cal {A}}~~\Pr(B)\neq 0\rightarrow \Pr(A\cap B)=\Pr(A\mid B)\Pr(B),$ мы можем показать эквивалентность приведенного выше утверждения, содержащего ( 1 ), и следующего утверждения: для всех $i\in I,~\Pr(X_{0}=i)=\lambda _{i}$ и для любого неотрицательного целого числа $n\geq 0$, для всех $t_{0},\dots ,t_{n+1}\in T$ такой, что $t_{0}<\dots <t_{n+1},$ для всех $i_{0},\dots ,i_{n+1}\in I$ такой, что $0<\Pr(X_{0}=i_{0},\dots ,X_{t_{n}}=i_{n})$ (следует, что $0<\Pr(X_{t_{n}}=i_{n})$),

$\Pr(X_{t_{n+1}}=i_{n+1}\mid X_{t_{n}}=i_{n},\dots ,X_{t_{0}}=i_{0})=P(t_{n+1}-t_{n})_{i_{n},i_{n+1}}.$ ( 2 )

Это следует из непрерывности функций $(P(t)_{i,j})_{t\in T}$ ( $i,j\in S$), что траектория $(X_{t}(\omega ))_{t\in T}$ почти наверняка непрерывен справа (относительно дискретной метрики на $S$): существует $\Pr$-нулевой набор $N$ такой, что $\{\omega \in \Omega :(X_{t}(\omega ))_{t\in T}{\text{ is right continuous}}\}\subseteq N$.

Определение цепочки переходов/времени удержания

Последовательности, связанные с непрерывной справа функцией

Позволять $f:T\to S$ быть правонепрерывным (когда мы оборудуем $S$ с дискретной метрикой ). Определять

$h=h(f)=(\inf\{u\in (0,+\infty ):f(t+u)\neq f(t)\})_{t\in T})\cup \{+\infty ,0\},$

позволять

$H=H(f)=(h^{\circ n}0)_{n\in \mathbb {Z} _{\geq 0}}$

быть последовательностью времени удержания, связанной с $f$, выбирать $s\in S,$ и пусть

$y=y(f)=\left({\begin{cases}f(\sum _{k\in n}H_{k})&{\text{ if }}\sum _{k\in n}H_{k}<+\infty ,\\s&{\text{ else}}\end{cases}}\right)_{n\in \omega }$

быть « последовательностью состояний », связанной с $f$.

Определение матрицы скачков Π

Матрица перехода $\Pi$, альтернативно написано $\Pi (Q)$ если мы хотим подчеркнуть зависимость от $Q$, – матрица

$$\Pi =([i=j])_{i\in Z,j\in S}\cup \bigcup _{i\in S\setminus Z}(\{((i,j),(-Q_{i,i})^{-1}Q_{i,j}):j\in S\setminus \{i\}\}\cup \{((i,i),0)\}),$$

где $Z=Z(Q)=\{k\in S:q_{k,k}=0\}$ — нулевое множество функции $(q_{k,k})_{k\in S}.$

Свойство цепочки переходов/времени удержания

Мы говорим $X$ является марковским с начальным распределением $\lambda$ и матрица ставок $Q$ означает: траектории $X$ почти наверняка непрерывны справа, пусть $f$ быть модификацией $X$ иметь (везде) правонепрерывные траектории, $\sum _{n\in \mathbb {Z} _{\geq 0}}H(f(\omega ))_{n}=+\infty$ почти наверняка (на заметку знатокам: это условие говорит $X$ невзрывоопасно), последовательность состояний $y(f(\omega ))$ представляет собой цепь Маркова с дискретным временем и начальным распределением $\lambda$ (свойство цепи перехода) и матрица перехода $\Pi (Q),$ и $\forall n\in \mathbb {Z} _{\geq 0}~\forall B\in {\cal {B}}(\mathbb {R} _{\geq 0})~\Pr(H_{n}(f)\in B)=\operatorname {Exp} (-q_{Y_{n},Y_{n}})(B)$ (имущество, находящееся во владении).

Бесконечно малое определение

Цепь Маркова с непрерывным временем характеризуется скоростями перехода, производными по времени вероятностей перехода между состояниями i и j.

Мы говорим $X$ является марковским с начальным распределением $\lambda$ и матрица ставок $Q$ иметь в виду: для всех $i\in S,$ $\Pr(X(0)=i)=\lambda _{i}$ и для всех $i,j$, для всех $t$ и для малых строго положительных значений $h$, то для всех справедливо следующее $t\in T$ такой, что $0<\Pr(X(t)=i)$:

$\Pr(X(t+h)=j\mid X(t)=i)=[i=j]+q_{i,j}h+o(h)$,

где термин $[i=j]$ является $1$ если $i=j$ и в противном случае $0$и термин «маленькое о» $o(h)$ зависит определенным образом от $i,j,h$.

Приведенное выше уравнение показывает, что $q_{i,j}$ можно рассматривать как измерение того, насколько быстро происходит переход от $i$ к $j$ происходит для $i\neq j$, и как быстро происходит переход от $i$ происходит для $i=j$.

Свойства

Общение классов

Коммуникирующие классы, быстротечность, рекуррентность, а также положительная и нулевая рекуррентность определяются так же, как и для цепей Маркова с дискретным временем .

Переходное поведение

Запишите P( t ) для матрицы с элементами p _ij = P( X _t = j | X ₀ = i ). Тогда матрица P( t ) удовлетворяет прямому уравнению, дифференциальному уравнению первого порядка

$P'(t)=P(t)Q$,

где штрих обозначает дифференцирование по t . Решение этого уравнения дается матричной экспонентой

$P(t)=e^{tQ}$.

В простом случае, таком как CTMC в пространстве состояний {1,2}. Общая матрица Q для такого процесса представляет собой следующую матрицу 2 × 2 с α , β > 0

$Q={\begin{pmatrix}-\alpha &\alpha \\\beta &-\beta \end{pmatrix}}.$

В этом случае приведенное выше соотношение для прямой матрицы можно решить явно, чтобы получить

$P(t)={\begin{pmatrix}{\frac {\beta }{\alpha +\beta }}+{\frac {\alpha }{\alpha +\beta }}e^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}-{\frac {\alpha }{\alpha +\beta }}e^{-(\alpha +\beta )t}\\{\frac {\beta }{\alpha +\beta }}-{\frac {\beta }{\alpha +\beta }}e^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}+{\frac {\beta }{\alpha +\beta }}e^{-(\alpha +\beta )t}\end{pmatrix}}$.

Вычисление прямых решений в больших матрицах затруднено. Тот факт, что Q является генератором полугруппы матриц

$P(t+s)=e^{(t+s)Q}=e^{tQ}e^{sQ}=P(t)P(s)$

используется.

Стационарное распространение

Стационарное распределение для неприводимого рекуррентного CTMC — это распределение вероятностей, к которому сходится процесс при больших значениях t . Заметим, что для рассмотренного ранее процесса с двумя состояниями с P( t ), заданным выражением

$P(t)={\begin{pmatrix}{\frac {\beta }{\alpha +\beta }}+{\frac {\alpha }{\alpha +\beta }}e^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}-{\frac {\alpha }{\alpha +\beta }}e^{-(\alpha +\beta )t}\\{\frac {\beta }{\alpha +\beta }}-{\frac {\beta }{\alpha +\beta }}e^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}+{\frac {\beta }{\alpha +\beta }}e^{-(\alpha +\beta )t}\end{pmatrix}}$,

при t → ∞ распределение стремится к

$P_{\pi }={\begin{pmatrix}{\frac {\beta }{\alpha +\beta }}&{\frac {\alpha }{\alpha +\beta }}\\{\frac {\beta }{\alpha +\beta }}&{\frac {\alpha }{\alpha +\beta }}\end{pmatrix}}$.

Обратите внимание, что каждая строка имеет одинаковое распределение, поскольку это не зависит от начального состояния. Вектор-строка π может быть найден путем решения

$\pi Q=0$

с ограничением

$\sum _{i\in S}\pi _{i}=1$.

Пример 1

Ориентированное графическое представление цепи Маркова с непрерывным временем, описывающей состояние финансовых рынков (примечание: числа вымышлены).

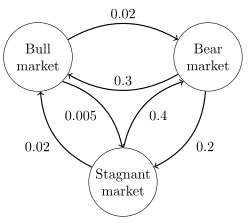
Изображение справа описывает цепь Маркова в непрерывном времени с пространством состояний {Бычий рынок, Медвежий рынок, Застойный рынок} и матрицей скорости перехода.

$Q={\begin{pmatrix}-0.025&0.02&0.005\\0.3&-0.5&0.2\\0.02&0.4&-0.42\end{pmatrix}}.$

Стационарное распределение этой цепочки можно найти, решив $\pi Q=0$, при условии, что сумма элементов должна быть равна 1, чтобы получить

$\pi ={\begin{pmatrix}0.885&0.071&0.044\end{pmatrix}}.$

Пример 2

Граф переходов с вероятностями перехода, примерный для состояний 1, 5, 6 и 8. Между состояниями 2 и 8 существует двусторонний секретный проход.

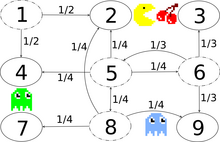
Изображение справа описывает цепь Маркова в дискретном времени, моделирующую Pac-Man с пространством состояний {1,2,3,4,5,6,7,8,9}. Игрок управляет Pac-Man через лабиринт, поедая пак-точки. Тем временем за ним охотятся призраки. Для удобства лабиринт должен представлять собой небольшую сетку 3х3, а призраки будут перемещаться случайным образом в горизонтальном и вертикальном направлениях. Секретный проход между состояниями 2 и 8 можно использовать в обоих направлениях. Записи с нулевой вероятностью удаляются в следующей матрице скорости перехода:

$Q={\begin{pmatrix}-1&{\frac {1}{2}}&&{\frac {1}{2}}\\{\frac {1}{4}}&-1&{\frac {1}{4}}&&{\frac {1}{4}}&&&{\frac {1}{4}}\\&{\frac {1}{2}}&-1&&&{\frac {1}{2}}\\{\frac {1}{3}}&&&-1&{\frac {1}{3}}&&{\frac {1}{3}}\\&{\frac {1}{4}}&&{\frac {1}{4}}&-1&{\frac {1}{4}}&&{\frac {1}{4}}\\&&{\frac {1}{3}}&&{\frac {1}{3}}&-1&&&{\frac {1}{3}}\\&&&{\frac {1}{2}}&&&-1&{\frac {1}{2}}\\&{\frac {1}{4}}&&&{\frac {1}{4}}&&{\frac {1}{4}}&-1&{\frac {1}{4}}\\&&&&&{\frac {1}{2}}&&{\frac {1}{2}}&-1\end{pmatrix}}$

Эта цепь Маркова несократима, поскольку призраки могут перелетать из каждого состояния в любое состояние за конечное время. Благодаря секретному ходу цепь Маркова также является апериодической, поскольку призраки могут переходить из любого состояния в любое состояние как за четное, так и за нечетное число переходов между состояниями. Следовательно, существует единственное стационарное распределение, которое можно найти, решив $\pi Q=0$, с учетом ограничения, согласно которому сумма элементов должна быть равна 1. Решение этого линейного уравнения с учетом ограничения есть $\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)\%.$Центральный штат и приграничные штаты 2 и 8 прилегающего секретного прохода посещаются больше всего, а угловые штаты посещаются меньше всего.

Обратное время

Для CTMC X _t обращенный во времени процесс определяется как ${\hat {X}}_{t}=X_{T-t}$. По лемме Келли этот процесс имеет такое же стационарное распределение, как и прямой процесс.

Цепь называется обратимой, если обратный процесс аналогичен прямому процессу. Критерий Колмогорова утверждает, что необходимым и достаточным условием обратимости процесса является то, что произведение скоростей перехода по замкнутому контуру должно быть одинаковым в обоих направлениях.

цепь

методов нахождения стационарного распределения вероятностей π эргодической цепи Одним из с непрерывным временем Маркова Q является сначала нахождение ее встроенной цепи Маркова (EMC) . Строго говоря, ЭМС представляет собой регулярную цепь Маркова с дискретным временем. Каждый элемент матрицы вероятности одношагового перехода EMC, S , обозначается sij _{условную} и представляет собой вероятность перехода из состояния i в состояние j . Эти условные вероятности можно найти с помощью

$s_{ij}={\begin{cases}{\frac {q_{ij}}{\sum _{k\neq i}q_{ik}}}&{\text{if }}i\neq j,\\0&{\text{otherwise}}.\end{cases}}$

Отсюда S можно записать как

$S=I-\left(\operatorname {diag} (Q)\right)^{-1}Q$

где I — единичная матрица , а Diag( Q ) — диагональная матрица, сформированная путем выбора главной диагонали из матрицы Q и установки всех остальных элементов в ноль.

Чтобы найти стационарный вектор распределения вероятностей, мы должны затем найти $\varphi$ такой, что

$\varphi S=\varphi ,$

с $\varphi$ являющийся вектором-строкой, такой, что все элементы в $\varphi$ больше 0 и $\|\varphi \|_{1}$ = 1. Отсюда π можно найти как

$\pi ={-\varphi (\operatorname {diag} (Q))^{-1} \over \left\|\varphi (\operatorname {diag} (Q))^{-1}\right\|_{1}}.$

( S может быть периодическим, даже если Q нет. Как только π найдено, его необходимо нормализовать на единичный вектор .)

Другой процесс с дискретным временем, который может быть получен из цепи Маркова с непрерывным временем, - это δ-скелет - цепь Маркова (с дискретным временем), образованная путем наблюдения X ( t ) с интервалами в δ единиц времени. Случайные величины X (0), X (δ), X (2δ),... задают последовательность состояний, которые посещает δ-скелет.

См. также

• Уравнения Колмогорова (марковский скачкообразный процесс)

Ссылки

• Андерсон, Уильям Дж. (1991). Цепи Маркова с непрерывным временем: прикладно-ориентированный подход . Спрингер.
• Лео Брейман (1992) [1968] Вероятность . Оригинальное издание опубликовано Аддисон-Уэсли; перепечатано Обществом промышленной и прикладной математики. ISBN   0-89871-296-3 . (См. главу 7)
• Чен, Му-Фа (2004). От цепей Маркова к неравновесным системам частиц (Второе изд.). Всемирная научная.
• Чен, Му-Фа; Мао, Юн-Хуа (2021). Введение в случайные процессы . Всемирная научная.
• Дж. Л. Дуб (1953) Стохастические процессы . Нью-Йорк: Джон Уайли и сыновья ISBN   0-471-52369-0 .
• А. А. Марков (1971). «Распространение предельных теорем теории вероятностей на сумму переменных, связанных в цепочку». перепечатано в Приложении B: Р. Ховард. Динамические вероятностные системы, том 1: Цепи Маркова . Джон Уайли и сыновья.
• Марков А.А. (2006). «Пример статистического исследования текста «Евгений Онегин» по поводу соединения образцов в цепочки». Наука в контексте . 19 (4). Перевод Линка, Дэвид: 591–600. дои : 10.1017/s0269889706001074 . S2CID   144854176 .
• С. П. Мейн и Р. Л. Твиди (1993) Марковские цепи и стохастическая устойчивость . Лондон: Спрингер-Верлаг ISBN   0-387-19832-6 . онлайн: МЦСС . Появится второе издание, Cambridge University Press, 2009 г.
• Кемени, Джон Г.; Хэзлтон Миркил; Дж. Лори Снелл; Джеральд Л. Томпсон (1959). Конечные математические структуры (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice-Hall, Inc. Номер карточного каталога Библиотеки Конгресса 59-12841. Классический текст. см. главу 6. Конечные цепи Маркова, стр. 384 и далее.
• Джон Г. Кемени и Дж. Лори Снелл (1960) Конечные цепи Маркова , компания Д. ван Ностранда ISBN   0-442-04328-7
• Э. Нуммелин. Общие неприводимые цепи Маркова и неотрицательные операторы . Издательство Кембриджского университета, 1984, 2004. ISBN   0-521-60494-X
• Норрис, младший (1997). Марковские цепи . дои : 10.1017/CBO9780511810633.005 . ISBN  9780511810633 .
• Сенета, Э. Неотрицательные матрицы и цепи Маркова . 2-я ред. изд., 1981, XVI, 288 стр., Серия Springer в мягкой обложке по статистике. (Первоначально опубликовано Allen & Unwin Ltd., Лондон, 1973 г.) ISBN   978-0-387-29765-1
• Сухов Юрий; Келберт, Марк (2008). Цепи Маркова: учебник случайных процессов и их приложений . Издательство Кембриджского университета.