коэффициент Зеебека

Коэффициент Зеебека (также известный как термоЭДС , термоэлектрическая мощность и термоэлектрическая чувствительность ) материала — это мера величины индуцированного термоэлектрического напряжения в ответ на разницу температур в этом материале, вызванную эффектом Зеебека . Единицей коэффициента Зеебека в системе СИ является вольт на кельвин (В/К), хотя чаще всего выражается в микровольтах на кельвин (мкВ/К).

Использование материалов с высоким коэффициентом Зеебека. является одним из многих важных факторов эффективного поведения термоэлектрических генераторов и термоэлектрических охладителей . Более подробную информацию о высокоэффективных термоэлектрических материалах можно найти в статье «Термоэлектрические материалы» . В термопарах для измерения температуры используется эффект Зеебека, причем для точности желательно использовать материалы с коэффициентом Зеебека, стабильным во времени.

Физически величину и знак коэффициента Зеебека можно приблизительно понимать как определяемые энтропией на единицу заряда, переносимого электрическими токами в материале. Оно может быть положительным или отрицательным. В проводниках, которые можно понимать как независимо движущиеся, почти свободные носители заряда , коэффициент Зеебека отрицательен для отрицательно заряженных носителей (таких как электроны ) и положителен для положительно заряженных носителей (таких как электронные дырки ).

Определение

Основная статья: эффект Зеебека

Одним из способов определения коэффициента Зеебека является напряжение, возникающее при приложении к материалу небольшого температурного градиента и когда материал пришел в устойчивое состояние, когда плотность тока везде равна нулю. Если разница температур Δ T между двумя концами материала невелика, то коэффициент Зеебека материала определяется как:

$S=-{\Delta V \over \Delta T}$

где Δ V — термоэлектрическое напряжение, наблюдаемое на клеммах. (Подробнее о знаках Δ V и Δ T см. ниже .)

Обратите внимание, что сдвиг напряжения, выраженный эффектом Зеебека, не может быть измерен напрямую, поскольку измеренное напряжение (путем подключения вольтметра) содержит дополнительный вклад напряжения из-за градиента температуры и эффекта Зеебека в измерительных выводах. Напряжение вольтметра всегда зависит от относительных коэффициентов Зеебека различных используемых материалов.

В наиболее общем и техническом плане коэффициент Зеебека определяется как доля электрического тока, обусловленная градиентами температуры, как в векторном дифференциальном уравнении.

$\mathbf {J} =-\sigma {\boldsymbol {\nabla }}V-\sigma S{\boldsymbol {\nabla }}T$

где $\scriptstyle \mathbf {J}$ плотность тока , $\scriptstyle \sigma$ – электропроводность , $\scriptstyle {\boldsymbol {\nabla }}V$ - градиент напряжения, а $\scriptstyle {\boldsymbol {\nabla }}T$ это градиент температуры. Описанный выше особый случай устойчивого состояния с нулевым током имеет $\scriptstyle \mathbf {J} =0$, что означает, что два члена электропроводности сократились, и поэтому ${\boldsymbol {\nabla }}V=-S{\boldsymbol {\nabla }}T.$

Соглашение о подписании

Знак явно выражен в следующем выражении:

$S=-{\frac {V_{\rm {left}}-V_{\rm {right}}}{T_{\rm {left}}-T_{\rm {right}}}}$

Таким образом, если S положительное, конец с более высокой температурой имеет более низкое напряжение, и наоборот. Градиент напряжения в материале будет направлен против градиента температуры.

В эффекте Зеебека обычно преобладает вклад диффузии носителей заряда (см. ниже), которая имеет тенденцию подталкивать носители заряда к холодной стороне материала до тех пор, пока не возникнет компенсирующее напряжение. В результате в полупроводниках p-типа (которые имеют только положительные подвижные заряды, электронные дырки ) S положителен. Аналогично, в полупроводниках n-типа (которые имеют только отрицательные подвижные заряды, электроны ) S отрицателен. Однако в большинстве проводников носители заряда проявляют как дырочное, так и электронное поведение, и знак S обычно зависит от того, какой из них преобладает.

Связь с другими термоэлектрическими коэффициентами

Основная статья: Отношения Томсона

Согласно второму соотношению Томсона (которое справедливо для всех немагнитных материалов в отсутствие внешнего магнитного поля) коэффициент Зеебека связан с коэффициентом Пельтье $\scriptstyle \Pi$ по точному соотношению

$S={\frac {\Pi }{T}},$

где $T$ – термодинамическая температура .

Согласно первому соотношению Томсона и при тех же предположениях о магнетизме коэффициент Зеебека связан с коэффициентом Томсона $\scriptstyle {\mathcal {K}}$ к

$S=\int {\frac {\mathcal {K}}{T}}\,dT.$

Константа интегрирования такова, что $\scriptstyle S=0$ при абсолютном нуле, как того требует теорема Нернста .

Измерение

Относительный коэффициент Зеебека

См. Также: Термопара

На практике абсолютный коэффициент Зеебека трудно измерить напрямую, поскольку выходное напряжение термоэлектрической цепи, измеренное вольтметром, зависит только от разности коэффициентов Зеебека. Это связано с тем, что для измерения термоэлектрического напряжения на материал необходимо поместить электроды, прикрепленные к вольтметру. Градиент температуры также обычно индуцирует термоэлектрическое напряжение на одном плече измерительных электродов. Следовательно, измеренный коэффициент Зеебека представляет собой вклад коэффициента Зеебека интересующего материала и материала измерительных электродов. Такое расположение двух материалов обычно называют термопарой .

Тогда измеренный коэффициент Зеебека является вкладом обоих и может быть записан как:

$S_{AB}=S_{B}-S_{A}={\Delta V_{B} \over \Delta T}-{\Delta V_{A} \over \Delta T}$

Абсолютный коэффициент Зеебека

Абсолютный коэффициент Зеебека свинца при низкой температуре по данным Кристиана, Яна, Пирсона, Темплтона (1958). Ниже критической температуры свинца (обозначенной пунктирной линией, примерно 7 К) свинец является сверхпроводящим.

Абсолютные коэффициенты Зеебека различных металлов до высоких температур, в основном из Cusack & Kendall (1958). Данные по свинцу (Pb) взяты из Christian, Jan, Pearson, Templeton (1958).

Хотя для внешних измерений напряжения важны только относительные коэффициенты Зеебека, абсолютный коэффициент Зеебека может быть важен для других эффектов, когда напряжение измеряется косвенно. Поэтому определение абсолютного коэффициента Зеебека требует более сложных методов и является более трудным, но такие измерения проводились на стандартных материалах. Эти измерения нужно было выполнить только один раз за все время и для всех материалов; для любого другого материала абсолютный коэффициент Зеебека можно получить путем измерения относительного коэффициента Зеебека относительно стандартного материала.

Измерение коэффициента Томсона ${\mathcal {K}}$, который выражает силу эффекта Томсона , можно использовать для получения абсолютного коэффициента Зеебека посредством соотношения: $S(T)=\int _{0}^{T}{{\mathcal {K}}(T') \over T'}dT'$, при условии, что ${\mathcal {K}}$ измеряется до абсолютного нуля . Причина, по которой это работает, заключается в том, что $S(T)$ ожидается, что она уменьшится до нуля при доведении температуры до нуля — следствие теоремы Нернста . Такое измерение основано на интегрировании ${\mathcal {K}}/T$ был опубликован в 1932 году, хотя он основывался на интерполяции коэффициента Томсона в определенных областях температуры.

Как указано ниже, сверхпроводники имеют нулевой коэффициент Зеебека. Сделав один из проводов термопары сверхпроводящим, можно получить прямое измерение абсолютного коэффициента Зеебека другого провода, поскольку он один определяет измеряемое напряжение со всей термопары. В публикации 1958 года этот метод использовался для измерения абсолютного коэффициента Зеебека свинца в диапазоне от 7,2 К до 18 К, тем самым заполняя важный пробел в предыдущем эксперименте 1932 года, упомянутом выше.

Комбинация метода сверхпроводник-термопара до 18 К с методом интегрирования коэффициентов Томсона выше 18 К позволила определить абсолютный коэффициент Зеебека свинца до комнатной температуры. Посредством этих измерений были определены абсолютные коэффициенты Зеебека для всех материалов , даже до более высоких температур, с помощью комбинации интегрирования коэффициентов Томсона и схем термопар.

Трудность этих измерений и редкость воспроизведения экспериментов придают некоторую степень неопределенности полученной таким образом абсолютной термоэлектрической шкале. В частности, измерения 1932 года могли неправильно измерить коэффициент Томсона в диапазоне от 20 К до 50 К. Поскольку почти все последующие публикации основывались на этих измерениях, это означало бы, что все обычно используемые значения абсолютного коэффициента Зеебека (включая показанные на рисунках) занижены примерно на 0,3 мкВ/К для всех температур выше 50 К.

Коэффициенты Зеебека для некоторых распространенных материалов

О термоэлектрических свойствах высокоэффективных термоэлектрических материалов см. Термоэлектрические материалы .

В таблице ниже приведены коэффициенты Зеебека при комнатной температуре для некоторых распространенных неэкзотических материалов, измеренные относительно платины. Коэффициент Зеебека самой платины составляет примерно -5 мкВ/К при комнатной температуре. поэтому значения, перечисленные ниже, должны быть соответствующим образом компенсированы. Например, коэффициенты Зеебека Cu, Ag, Au составляют 1,5 мкВ/К, а Al -1,5 мкВ/К. Коэффициент Зеебека полупроводников во многом зависит от легирования: обычно он имеет положительные значения для материалов, легированных p, и отрицательные значения для легирования n.

Материал	коэффициент Зеебека относительно платины (мкВ/К)
Селен	900
Теллур	500
Кремний	440
германий	330
Сурьма	47
нихром	25
Железо	19
Молибден	10
Кадмий , вольфрам	7.5
Золото , серебро , медь	6.5
Родий	6.0
Тантал	4.5
Вести	4.0
Алюминий	3.5
Углерод	3.0
Меркурий	0.6
Платина	0 (определение)
Натрий	-2.0
Калий	-9.0
Никель	-15
Константан	-35
Висмут	-72

Физические факторы, определяющие коэффициент Зеебека

Температура материала, кристаллическая структура и примеси влияют на значение термоэлектрических коэффициентов. Эффект Зеебека можно объяснить двумя вещами: диффузия носителей заряда и увлечение фононов.

Диффузия носителей заряда

На фундаментальном уровне приложенная разность напряжений относится к разнице термодинамических химических потенциалов носителей заряда, а направление тока под разностью напряжений определяется универсальным термодинамическим процессом, в котором (при равных температурах) частицы текут из высоких химического потенциала до низкого химического потенциала. Другими словами, направление тока в законе Ома определяется термодинамической стрелой времени (разница в химическом потенциале может быть использована для производства работы, но вместо этого рассеивается в виде тепла, что увеличивает энтропию). С другой стороны, для эффекта Зеебека с помощью термодинамики невозможно предсказать даже знак тока, и поэтому, чтобы понять происхождение коэффициента Зеебека, необходимо понять микроскопическую физику.

Носители заряда (например, термически возбужденные электроны) постоянно диффундируют внутри проводящего материала. Из-за тепловых флуктуаций некоторые из этих носителей заряда движутся с энергией выше средней, а некоторые — с меньшей. Когда нет разницы напряжений или разницы температур, диффузия носителей идеально уравновешивается, и поэтому в среднем ток не наблюдается: $\scriptstyle \mathbf {J} =0$. Полезный ток может быть создан путем применения разницы напряжений (закон Ома) или путем применения разницы температур (эффект Зеебека). Чтобы понять микроскопическую природу термоэлектрического эффекта, полезно сначала описать микроскопический механизм электропроводности по нормальному закону Ома — описать, что определяет $\scriptstyle \sigma$ в $\scriptstyle \mathbf {J} =-\sigma {\boldsymbol {\nabla }}V$. С микроскопической точки зрения в законе Ома происходит следующее: более высокие энергетические уровни имеют более высокую концентрацию носителей в каждом состоянии на стороне с более высоким химическим потенциалом. Для каждого интервала энергии носители имеют тенденцию диффундировать и распространяться в ту область устройства, где на одно состояние этой энергии приходится меньше носителей. Однако по мере движения они иногда диссипативно рассеиваются, что приводит к повторному рандомизации их энергии в соответствии с местной температурой и химическим потенциалом. Эта диссипация выводит носители из этих более высоких энергетических состояний, позволяя большему количеству диффундировать внутрь. Сочетание диффузии и диссипации способствует общему дрейфу носителей заряда к той стороне материала, где они имеют более низкий химический потенциал.

Что касается термоэлектрического эффекта, рассмотрим теперь случай однородного напряжения (однородного химического потенциала) с температурным градиентом. При этом на более горячей стороне материала изменение энергий носителей заряда больше, чем на более холодной стороне. Это означает, что уровни с высокими энергиями имеют более высокую занятость носителей в каждом состоянии на более горячей стороне, но также более горячая сторона имеет меньшую занятость в каждом состоянии на более низких энергетических уровнях. Как и раньше, носители высокой энергии диффундируют от горячего конца устройства и производят энтропию, дрейфуя к холодному концу устройства. Однако имеет место конкурирующий процесс: при этом носители низкой энергии оттягиваются обратно к горячему концу устройства. Хотя оба этих процесса генерируют энтропию, они действуют друг против друга с точки зрения тока заряда, поэтому чистый ток возникает только в том случае, если один из этих дрейфов сильнее другого. Чистый ток определяется выражением $\scriptstyle \mathbf {J} =-\sigma S{\boldsymbol {\nabla }}T$, где (как показано ниже) коэффициент термоЭДС $\scriptstyle \sigma S$ буквально зависит от того, насколько проводящими являются носители высокой энергии по сравнению с носителями низкой энергии. Различие может быть связано с разницей в скорости рассеяния, разницей в скоростях, разницей в плотности состояний или комбинацией этих эффектов.

Формула Мотта

Описанные выше процессы применяются к материалам, где каждый носитель заряда находится в по существу статичной среде, так что его движение можно описать независимо от других носителей и независимо от другой динамики (например, фононов). В частности, в электронных материалах со слабыми электрон-электронными взаимодействиями, слабыми электрон-фононными взаимодействиями и т. д. в общем можно показать, что линейная откликовая проводимость равна

$\sigma =\int c(E){\Bigg (}-{\frac {df(E)}{dE}}{\Bigg )}\,dE,$

а коэффициент термоЭДС линейного отклика равен

$\sigma S={\frac {k_{\rm {B}}}{-e}}\int {\frac {E-\mu }{k_{\rm {B}}T}}c(E){\Bigg (}-{\frac {df(E)}{dE}}{\Bigg )}\,dE$

где $\scriptstyle c(E)$ – энергозависимая проводимость, а $\scriptstyle f(E)$ – функция распределения Ферми–Дирака . Эти уравнения известны как соотношения Мотта сэра Невилла Фрэнсиса Мотта . Производная

$-{\frac {df(E)}{dE}}={\frac {1}{4k_{\rm {B}}T}}\operatorname {sech} ^{2}\left({\frac {E-\mu }{2k_{\rm {B}}T}}\right)$

представляет собой функцию с максимумом вблизи химического потенциала ( уровня Ферми ). $\mu$ шириной ​ примерно $3.5k_{\rm {B}}T$. Энергозависимая проводимость (величина, которую на самом деле невозможно измерить напрямую — можно только измерить $\sigma$) рассчитывается как $c(E)=e^{2}D(E)\nu (E)$ где $D(E)$ электронов - константа диффузии и $\nu (E)$ — электронная плотность состояний (вообще, обе функции являются функциями энергии).

В материалах с сильными взаимодействиями ни одно из приведенных выше уравнений нельзя использовать, поскольку невозможно рассматривать каждый носитель заряда как отдельную сущность. Закон Видемана -Франца также можно точно вывести, используя картину невзаимодействующих электронов, и поэтому в материалах, где закон Видемана-Франца не работает (например, в сверхпроводниках ), соотношения Мотта также обычно имеют тенденцию не работать.

Приведенные выше формулы можно упростить в нескольких важных предельных случаях:

Формула Мотта в металлах

В полуметаллах и металлах , где транспорт происходит только вблизи уровня Ферми и $\scriptstyle c(E)$ медленно меняется в диапазоне $E\approx \mu \pm k_{\rm {B}}T$, можно выполнить разложение Зоммерфельда $\scriptstyle c(E)=c(\mu )+c'(\mu )(E-\mu )+O[(E-\mu )^{2}]$, что приводит к

$S_{\rm {metal}}={\frac {\pi ^{2}k_{\rm {B}}^{2}T}{-3e}}{\frac {c'(\mu )}{c(\mu )}}+O[(k_{\rm {B}}T)^{3}],\quad \sigma _{\rm {metal}}=c(\mu )+O[(k_{\rm {B}}T)^{2}].$

Это выражение иногда называют «формулой Мотта», однако оно гораздо менее общее, чем исходная формула Мотта, выраженная выше.

В модели свободных электронов с рассеянием значение $\scriptstyle c'(\mu )/c(\mu )$ в порядке $\scriptstyle 1/(k_{\rm {B}}T_{\rm {F}})$, где $T_{\rm {F}}$ — температура Ферми , поэтому типичное значение коэффициента Зеебека в ферми-газе равно $\scriptstyle S_{\rm {Fermi~gas}}\approx {\tfrac {\pi ^{2}k_{\rm {B}}}{-3e}}T/T_{\rm {F}}$ (префактор несколько меняется в зависимости от таких деталей, как размерность и рассеяние). В металлах с высокой проводимостью температура Ферми обычно составляет около 10 ⁴ – 10 ⁵ K, поэтому понятно, почему их абсолютные коэффициенты Зеебека составляют всего лишь порядка 1 – 10 мкВ/К при комнатной температуре. Обратите внимание: хотя модель свободных электронов предсказывает отрицательный коэффициент Зеебека, реальные металлы на самом деле имеют сложную зонную структуру и могут иметь положительные коэффициенты Зеебека (примеры: Cu, Ag, Au).

Фракция $\scriptstyle c'(\mu )/c(\mu )$ в полуметаллах иногда рассчитывают по измеренной производной $\scriptstyle \sigma _{\rm {metal}}$ по отношению к некоторому сдвигу энергии, вызванному эффектом поля . Это не обязательно верно, и оценка $\scriptstyle c'(\mu )/c(\mu )$ может быть неверным (в два и более раз), так как потенциал беспорядка зависит от экранирования, которое также меняется с действием поля.

Формула Мотта в полупроводниках

В полупроводниках при низких уровнях легирования транспорт происходит только вдали от уровня Ферми. При малом легировании в зоне проводимости (где $\scriptstyle E_{\rm {C}}-\mu \gg k_{\rm {B}}T$, где $\scriptstyle E_{\rm {C}}$ – минимальная энергия края зоны проводимости), имеем $\scriptstyle -{\frac {df(E)}{dE}}\approx {\tfrac {1}{k_{\rm {B}}T}}e^{-(E-\mu )/(k_{\rm {B}}T)}$. Аппроксимируя функцию проводимости уровней зоны проводимости как $\scriptstyle c(E)=A_{\rm {C}}(E-E_{\rm {C}})^{a_{\rm {C}}}$ для некоторых констант $\scriptstyle A_{\rm {C}}$ и $\scriptstyle a_{\rm {C}}$,

$S_{\rm {C}}={\frac {k_{\rm {B}}}{-e}}{\Big [}{\frac {E_{\rm {C}}-\mu }{k_{\rm {B}}T}}+a_{\rm {C}}+1{\Big ]},\quad \sigma _{\rm {C}}=A_{\rm {C}}(k_{\rm {B}}T)^{a_{\rm {C}}}e^{-{\frac {E_{\rm {C}}-\mu }{k_{\rm {B}}T}}}\Gamma (a_{\rm {C}}+1).$

тогда как в валентной зоне, когда $\scriptstyle \mu -E_{\rm {V}}\gg kT$ и $\scriptstyle c(E)=A_{\rm {V}}(E_{\rm {V}}-E)^{a_{\rm {V}}}$,

$S_{\rm {V}}={\frac {k}{e}}{\Big [}{\frac {\mu -E_{\rm {V}}}{k_{\rm {B}}T}}+a_{\rm {V}}+1{\Big ]},\quad \sigma _{\rm {V}}=A_{\rm {V}}(k_{\rm {B}}T)^{a_{\rm {V}}}e^{-{\frac {\mu -E_{\rm {V}}}{k_{\rm {B}}T}}}\Gamma (a_{\rm {V}}+1).$

Значения $\scriptstyle a_{\rm {C}}$ и $\scriptstyle a_{\rm {V}}$ зависеть от материальных деталей; в объемном полупроводнике эти константы находятся в диапазоне от 1 до 3, причем крайние значения соответствуют рассеянию на решетке акустических мод и рассеянию на ионизированных примесях.

Коэффициент Зеебека кремния при 300 К, рассчитанный по модели Мотта. Переход от дырочной проводимости (положительная $\scriptstyle S\approx S_{\rm {V}}$) к проводимости с преобладанием электронов (отрицательная $\scriptstyle S\approx S_{\rm {C}}$) происходит для уровней Ферми в середине щели шириной 1,1 эВ.

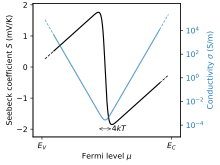
В внешних (легированных) полупроводниках при переносе будет доминировать либо зона проводимости, либо валентная зона, поэтому одно из приведенных выше чисел будет давать измеренные значения. Однако в целом полупроводник также может быть собственным, и в этом случае зоны проводят параллельно, и поэтому измеренные значения будут

$S_{\rm {semi}}={\frac {\sigma _{\rm {C}}S_{\rm {C}}+\sigma _{\rm {V}}S_{\rm {V}}}{\sigma _{\rm {C}}+\sigma _{\rm {V}}}},\quad \sigma _{\rm {semi}}=\sigma _{\rm {C}}+\sigma _{\rm {V}}$

Это приводит к перекрестному поведению, как показано на рисунке.Самый высокий коэффициент Зеебека получается, когда полупроводник слегка легирован, однако высокий коэффициент Зеебека сам по себе не обязательно полезен. Для термоэлектрических силовых устройств (охладителей, генераторов) более важно максимизировать коэффициент термоэлектрической мощности. $\scriptstyle \sigma S^{2}$, или термоэлектрическая эффективность , и оптимум обычно достигается при высоких уровнях легирования.

Фононное сопротивление

Основная статья: Фононное сопротивление

Фононы не всегда находятся в локальном тепловом равновесии; они движутся против температурного градиента. Они теряют импульс из-за взаимодействия с электронами (или другими носителями) и дефектами кристалла. Если фонон-электронное взаимодействие является преобладающим, фононы будут стремиться подтолкнуть электроны к одному концу материала, следовательно, теряя импульс и внося вклад в термоэлектрическое поле. Этот вклад наиболее важен в области температур, где преобладает фонон-электронное рассеяние. Это происходит за

$T\approx {1 \over 5}\theta _{\mathrm {D} }$

где $\scriptstyle \theta _{\rm {D}}$ — температура Дебая . При более низких температурах меньше фононов доступно для сопротивления, а при более высоких температурах они имеют тенденцию терять импульс в результате фонон-фононного рассеяния, а не фонон-электронного рассеяния. При более низких температурах границы материала также играют все большую роль, поскольку фононы могут перемещаться на значительные расстояния. Практически говоря, фононное увлечение является важным эффектом в полупроводниках при температурах, близких к комнатной (хотя и значительно выше $\scriptstyle \theta _{\rm {D}}/5$), что по величине сравнимо с эффектом диффузии носителей, описанным в предыдущем разделе.

Эта область зависимости термоЭДС от температуры сильно меняется под действием магнитного поля.

Связь с энтропией

Коэффициент Зеебека материала термодинамически соответствует количеству энтропии, «уносимой» потоком заряда внутри материала; в некотором смысле это энтропия на единицу заряда материала.