Случайный лес

Эта статья о технике машинного обучения. Информацию о других видах случайного дерева см. в разделе «Случайное дерево» .

Случайные леса или леса случайных решений — это метод ансамблевого обучения для классификации , регрессии и других задач, который работает путем построения множества деревьев решений во время обучения. Для задач классификации выходными данными случайного леса является класс, выбранный большинством деревьев. Для задач регрессии возвращается среднее или среднее предсказание отдельных деревьев. Случайные леса решений корректируют привычку деревьев решений подстраиваться под свой обучающий набор .

Первый алгоритм для леса случайных решений был создан в 1995 году Тином Кам Хо. используя метод случайных подпространств , что, по формулировке Хо, является способом реализации подхода «стохастической дискриминации» к классификации, предложенного Юджином Кляйнбергом.

Расширение алгоритма было разработано Лео Брейманом. и Адель Катлер , кто зарегистрировался «Случайные леса» как товарный знак в 2006 г. (по состоянию на 2019 г. , принадлежащий Minitab, Inc. ). Расширение сочетает в себе идею « упаковки » Бреймана и случайный выбор функций, впервые представленный Хо. а позже независимо Амита и Гемана для построения набора деревьев решений с контролируемой дисперсией.

История

Общий метод лесов случайных решений был впервые предложен Зальцбергом и Хитом в 1993 году. с методом, который использовал алгоритм рандомизированного дерева решений для создания нескольких разных деревьев, а затем объединял их с помощью голосования большинством. Эта идея была развита Хо в 1995 году. Хо установил, что леса деревьев, разделенные наклонными гиперплоскостями, могут получать точность по мере роста, не страдая от переобучения, при условии, что леса случайным образом ограничены чувствительностью только к выбранным размерам объектов . Последующая работа в том же духе пришли к выводу, что другие методы разделения ведут себя аналогичным образом, пока они случайным образом вынуждены быть нечувствительными к некоторым размерам объектов. Обратите внимание, что это наблюдение за тем, как более сложный классификатор (большой лес) становится более точным почти монотонно, резко контрастирует с распространенным убеждением, что сложность классификатора может вырасти только до определенного уровня точности, прежде чем она пострадает от переобучения. Объяснение устойчивости метода леса к перетренированности можно найти в теории стохастической дискриминации Клейнберга.

На раннее развитие идеи Бреймана о случайных лесах повлияли работы Амита и Гемана. который представил идею поиска по случайному подмножеству доступных решений при разделении узла в контексте выращивания одного дерева . Идея случайного выбора подпространства от Хо также оказал влияние на создание случайных лесов. В этом методе выращивается лес деревьев, и различия между деревьями вводятся путем проецирования обучающих данных в случайно выбранное подпространство перед подгонкой каждого дерева или каждого узла. Наконец, идея рандомизированной оптимизации узлов, при которой решение в каждом узле выбирается с помощью рандомизированной процедуры, а не детерминированной оптимизации, была впервые предложена Томасом Г. Диттерихом .

Правильное введение случайных лесов было сделано в статье Лео Бреймана . В этой статье описывается метод построения леса некоррелированных деревьев с использованием процедуры, подобной CART , в сочетании со рандомизированной оптимизацией узлов и пакетированием . Кроме того, в этой статье сочетаются несколько ингредиентов, как ранее известных, так и новых, которые составляют основу современной практики случайных лесов, в частности:

1. Использование ошибки «вне пакета» в качестве оценки ошибки обобщения .
2. Измерение важности переменной посредством перестановки.

В докладе также представлен первый теоретический результат для случайных лесов в виде оценки ошибки обобщения , которая зависит от силы деревьев в лесу и их корреляции .

Алгоритм

Предварительные сведения: изучение дерева решений

Основная статья: Обучение дереву решений

Деревья решений — популярный метод для решения различных задач машинного обучения. Обучение деревьям «наиболее близко соответствует требованиям, предъявляемым к использованию в качестве готовой процедуры интеллектуального анализа данных», говорят Хасти и др. , «поскольку он инвариантен при масштабировании и различных других преобразованиях значений признаков, устойчив к включению нерелевантных признаков и создает проверяемые модели. Однако они редко бывают точными».

В частности, деревья, выросшие очень глубоко, имеют тенденцию обучаться крайне нерегулярным шаблонам: они переопределяют свои обучающие наборы, т. е. имеют низкую систематическую ошибку, но очень высокую дисперсию . Случайные леса — это способ усреднения нескольких глубоких деревьев решений, обученных на разных частях одного и того же обучающего набора, с целью уменьшения дисперсии. Это достигается за счет небольшого увеличения систематической ошибки и некоторой потери интерпретируемости, но в целом значительно повышает производительность окончательной модели.

Упаковка

Основная статья: Агрегация Bootstrap

Иллюстрация обучения модели случайного леса. Набор обучающих данных (в данном случае из 250 строк и 100 столбцов) выбирается случайным образом с заменой n раз. Затем на каждой выборке обучается дерево решений. Наконец, для прогнозирования результаты всех n деревьев объединяются для принятия окончательного решения.

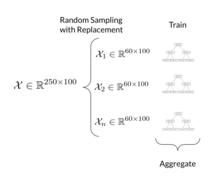
Алгоритм обучения случайных лесов применяет к обучающимся деревьям общий метод бутстрап-агрегирования или пакетирования. Учитывая обучающий набор X = x ₁ , ..., x _n с ответами Y = y ₁ , ..., y _n , повторное пакетирование ( B раз) выбирает случайную выборку с заменой обучающего набора и подбирает к ним деревья. образцы:

Для b = 1, ..., B :

1. Выборка с заменой n обучающих примеров из X , Y ; назовите их X _b , Y _b .
2. Обучите дерево классификации или регрессии f _b на X _b , Y _b .

После обучения прогнозы для невидимых выборок x' можно сделать путем усреднения прогнозов всех отдельных деревьев регрессии по x' :

$${\hat {f}}={\frac {1}{B}}\sum _{b=1}^{B}f_{b}(x')$$

или путем голосования большинства в случае деревьев классификации.

Эта процедура начальной загрузки приводит к повышению производительности модели, поскольку уменьшает дисперсию модели без увеличения систематической ошибки. Это означает, что, хотя прогнозы одного дерева очень чувствительны к шуму в его обучающем наборе, среднее значение многих деревьев нет, пока деревья не коррелированы. Простое обучение многих деревьев на одном обучающем наборе приведет к получению сильно коррелированных деревьев (или даже одного и того же дерева много раз, если алгоритм обучения является детерминированным); Бутстрап-выборка — это способ декорреляции деревьев путем показа им различных обучающих наборов.

Кроме того, оценку неопределенности прогноза можно сделать как стандартное отклонение прогнозов всех отдельных деревьев регрессии по x' : $$\sigma ={\sqrt {\frac {\sum _{b=1}^{B}(f_{b}(x')-{\hat {f}})^{2}}{B-1}}}.$$

Количество выборок/деревьев B является свободным параметром. Обычно используется от нескольких сотен до нескольких тысяч деревьев, в зависимости от размера и характера обучающего набора. Оптимальное количество деревьев B можно найти с помощью перекрестной проверки или путем наблюдения за ошибкой «вне пакета» : средней ошибкой прогнозирования для каждой обучающей выборки x _i с использованием только тех деревьев, у которых не было x _i в их начальной выборке. . Ошибка обучения и тестирования имеет тенденцию выравниваться после того, как некоторое количество деревьев было подобрано.

От упаковки в случайные леса

Основная статья: Метод случайного подпространства

Вышеуказанная процедура описывает исходный алгоритм упаковки деревьев. Случайные леса также включают в себя другой тип схемы объединения: они используют модифицированный алгоритм обучения дерева, который выбирает при каждом разделении кандидатов в процессе обучения случайное подмножество функций . Этот процесс иногда называют «сборкой функций». Причиной этого является корреляция деревьев в обычной бутстреп-выборке: если один или несколько признаков являются очень сильными предикторами для переменной ответа (целевой результат), эти признаки будут выбраны во многих B -деревьях, что приведет к их стать коррелированным. Анализ того, как пакетирование и случайное проецирование подпространства способствуют повышению точности в различных условиях, проведен Хо.

Обычно для задачи классификации с p признаками √ p (округленных вниз) признаков. в каждом разбиении используется Для задач регрессии изобретатели рекомендуют p /3 (округленное вниз) с минимальным размером узла 5 по умолчанию. На практике оптимальные значения этих параметров следует подбирать индивидуально для каждой проблемы.

Экстрадеревья

Добавление еще одного шага рандомизации дает чрезвычайно рандомизированные деревья или ExtraTrees. Несмотря на то, что они похожи на обычные случайные леса в том, что они представляют собой ансамбль отдельных деревьев, есть два основных различия: во-первых, каждое дерево обучается с использованием всей обучающей выборки (а не бутстрап-выборки), а во-вторых, разбиение сверху вниз в обучаемый дерево рандомизировано. Вместо вычисления локально оптимальной точки отсечения для каждого рассматриваемого признака (на основе, например, прироста информации или примеси Джини ), случайная выбирается точка отсечения. Это значение выбирается из равномерного распределения в пределах эмпирического диапазона признака (в обучающем наборе дерева). Затем из всех случайно сгенерированных разделений для разделения узла выбирается разделение, которое дает наивысший балл. Подобно обычным случайным лесам, можно указать количество случайно выбранных объектов, которые будут учитываться в каждом узле. Значения по умолчанию для этого параметра: ${\sqrt {p}}$ для классификации и $p$ для регрессии, где $p$ количество функций в модели.

Случайные леса для многомерных данных

Базовая процедура случайного леса может не работать хорошо в ситуациях, когда имеется большое количество признаков, но лишь небольшая часть этих признаков информативна для классификации выборки. Эту проблему можно решить, поощряя процедуру фокусироваться главным образом на информативных функциях и деревьях. Вот некоторые методы достижения этой цели:

• Предварительная фильтрация: удаление функций, которые в основном представляют собой просто шум.
• Обогащенный случайный лес (ERF): используйте взвешенную случайную выборку вместо простой случайной выборки в каждом узле каждого дерева, придавая больший вес функциям, которые кажутся более информативными.
• Случайный лес, взвешенный по деревьям (TWRF): взвешивайте деревья, чтобы деревьям, демонстрирующим более высокую точность, присваивались более высокие веса.

Характеристики

Переменная важность

Случайные леса можно использовать для естественного ранжирования важности переменных в задаче регрессии или классификации. Следующая техника была описана в оригинальной статье Бреймана. и реализован в R пакете randomForest .

Важность перестановки

Первый шаг в измерении важности переменной в наборе данных ${\mathcal {D}}_{n}=\{(X_{i},Y_{i})\}_{i=1}^{n}$ заключается в подгонке случайного леса к данным. В процессе подгонки ошибка выхода из пакета для каждой точки данных записывается и усредняется по лесу (ошибки на независимом тестовом наборе могут быть заменены, если во время обучения не используется пакетирование).

Чтобы измерить важность $j$-й признак после обучения, значения $j$-й признак переставляется в выборках «вне пакета», и ошибка «вне пакета» снова вычисляется на этом искаженном наборе данных. Оценка важности для $j$-й признак вычисляется путем усреднения разницы ошибок выхода из пакета до и после перестановки по всем деревьям. Оценка нормализуется по стандартному отклонению этих различий.

Функции, которые дают большие значения для этой оценки, оцениваются как более важные, чем функции, которые дают маленькие значения. Статистическое определение показателя значимости переменной было дано и проанализировано Zhu et al.

Этот метод определения важности переменной имеет некоторые недостатки.

• Для данных, включающих категориальные переменные с разным количеством уровней, случайные леса смещаются в пользу атрибутов с большим количеством уровней. Такие методы, как частичные перестановки и выращивание непредвзятых деревьев можно использовать для решения проблемы.
• Если данные содержат группы коррелированных характеристик, имеющих одинаковое значение для выходных данных, то меньшие группы имеют преимущество перед более крупными.
• Кроме того, процедура перестановки может не идентифицировать важные функции, если есть коллинеарные функции. В этом случае решением проблемы является перестановка групп коррелирующих признаков.

Среднее снижение важности примесных свойств

Эта функция, важная для случайных лесов, является реализацией по умолчанию в научных наборах и R. Она описана в книге Лео Бреймана «Деревья классификации и регрессии». Важными считаются переменные, которые значительно уменьшают примеси во время разделения: $${\text{unormalized average importance}}(x)={\frac {1}{n_{T}}}\sum _{i=1}^{n_{T}}\sum _{{\text{node }}j\in T_{i}|{\text{split variable}}(j)=x}p_{T_{i}}(j)\Delta i_{T_{i}}(j),$$ где $x$ указывает на особенность, $n_{T}$ количество деревьев в лесу, $T_{i}$ указывает на дерево $i$, $p_{T_{i}}(j)={\frac {n_{j}}{n}}$ это доля выборок, достигающих узла $j$, $\Delta i_{T_{i}}(j)$ это изменение примеси в дереве $t$ в узле $j$. В качестве меры примеси для образцов, попадающих в узел, можно использовать, например, следующую статистику:

• энтропия
• Коэффициент Джини
• Среднеквадратическая ошибка

Нормализованная важность затем получается путем нормализации всех признаков, так что сумма нормализованных важностей признаков равна 1.

Реализация по умолчанию среднего снижения важности примесных функций в научном наборе для изучения подвержена вводящим в заблуждение значениям функций:

• мера важности предпочитает функции с высокой мощностью
• он использует статистику обучения и, следовательно, не «отражает способность функции быть полезной для составления прогнозов, которые обобщаются для тестового набора»

Отношения с ближайшими соседями

На связь между случайными лесами и алгоритмом k -ближайшего соседа ( k -NN) указали Лин и Чон в 2002 году. Оказывается, обе схемы можно рассматривать как так называемые схемы взвешенных окрестностей . Это модели, построенные на основе обучающего набора. $\{(x_{i},y_{i})\}_{i=1}^{n}$ которые делают прогнозы ${\hat {y}}$ для новых точек x' , рассматривая «окрестность» точки, формализованную весовой функцией W : $${\hat {y}}=\sum _{i=1}^{n}W(x_{i},x')\,y_{i}.$$

Здесь, $W(x_{i},x')$ - неотрицательный вес i -й точки обучения относительно новой точки x' в том же дереве. Для любого конкретного x' веса точек $x_{i}$ сумма должна быть равна единице. Весовые функции задаются следующим образом:

• В k -NN веса равны $W(x_{i},x')={\frac {1}{k}}$ если x _i — одна из k точек, ближайших к x' , и ноль в противном случае.
• На дереве, $W(x_{i},x')={\frac {1}{k'}}$ если x _i — одна из k' точек того же листа, что и x' , и ноль в противном случае.

Поскольку лес усредняет предсказания набора из m деревьев с отдельными весовыми функциями $W_{j}$, его предсказания $${\hat {y}}={\frac {1}{m}}\sum _{j=1}^{m}\sum _{i=1}^{n}W_{j}(x_{i},x')\,y_{i}=\sum _{i=1}^{n}\left({\frac {1}{m}}\sum _{j=1}^{m}W_{j}(x_{i},x')\right)\,y_{i}.$$

Это показывает, что весь лес снова представляет собой схему взвешенного соседства с весами, усредняющими веса отдельных деревьев. Соседями точки x' в этой интерпретации являются точки $x_{i}$ общий лист на любом дереве $j$. Таким образом, окрестность x' сложным образом зависит от структуры деревьев и, следовательно, от структуры обучающего набора. Лин и Чон показывают, что форма окрестности, используемая случайным лесом, адаптируется к локальной важности каждого объекта.

Неконтролируемое обучение со случайными лесами

В рамках своей конструкции случайные лесные предикторы естественным образом приводят к показателю различия между наблюдениями. Можно также определить меру различия случайного леса между немаркированными данными: идея состоит в том, чтобы построить предиктор случайного леса, который отличает «наблюдаемые» данные от сгенерированных соответствующим образом синтетических данных. Наблюдаемые данные представляют собой исходные немаркированные данные, а синтетические данные взяты из эталонного распределения. Случайное несходство леса может быть привлекательным, поскольку оно очень хорошо обрабатывает смешанные типы переменных, инвариантно к монотонным преобразованиям входных переменных и устойчиво к внешним наблюдениям. Случайное несходство леса легко справляется с большим количеством полунепрерывных переменных благодаря выбору внутренних переменных; например, различие случайного леса «Addcl 1» взвешивает вклад каждой переменной в зависимости от того, насколько она зависит от других переменных. Случайное несходство леса использовалось в различных приложениях, например, для поиска групп пациентов на основе данных тканевых маркеров.

Варианты

Вместо деревьев решений были предложены и оценены линейные модели в качестве базовых оценок в случайных лесах, в частности, полиномиальная логистическая регрессия и наивные классификаторы Байеса . В тех случаях, когда связь между предикторами и целевой переменной является линейной, базовые учащиеся могут иметь такую ​​же высокую точность, как и ансамблевый учащийся.

Случайный лес ядра

В машинном обучении случайные леса ядра (KeRF) устанавливают связь между случайными лесами и методами ядра . Немного изменив их определение, случайные леса можно переписать в методы ядра , которые более интерпретируются и легче анализируются.

История

Лео Брейман был первым, кто заметил связь между случайным лесом и методами ядра . Он отметил, что случайные леса, которые выращиваются с использованием случайных векторов iid при построении дерева, эквивалентны ядру, действующему на истинное поле. Лин и Чон установил связь между случайными лесами и адаптивным ближайшим соседом, подразумевая, что случайные леса можно рассматривать как адаптивные оценки ядра. Дэвис и Гахрамани предложил ядро ​​случайного леса и показал, что оно может эмпирически превосходить современные методы ядра. Скорнет впервые определил оценки KeRF и установил явную связь между оценками KeRF и случайным лесом. Он также дал явные выражения для ядер, основанных на центрированном случайном лесу. и однородный случайный лес, две упрощенные модели случайного леса. Он назвал эти два KeRF «Центрированным KeRF» и «Униформным KeRF» и доказал верхние границы их согласованности.

Обозначения и определения

Предварительные сведения: центрированные леса

Центрированный лес представляет собой упрощенную модель исходного случайного леса Бреймана, которая равномерно выбирает атрибут среди всех атрибутов и выполняет разбиение в центре ячейки вдоль заранее выбранного атрибута. Алгоритм останавливается, когда полностью бинарное дерево уровня $k$ построен там, где $k\in \mathbb {N}$ является параметром алгоритма.

Равномерный лес

Равномерный лес — это еще одна упрощенная модель исходного случайного леса Бреймана, которая равномерно выбирает объект среди всех объектов и выполняет разбиение в точке, равномерно нарисованной на боковой стороне ячейки вдоль заранее выбранного объекта.

От случайного леса к KeRF

Учитывая обучающую выборку ${\mathcal {D}}_{n}=\{(\mathbf {X} _{i},Y_{i})\}_{i=1}^{n}$ из $[0,1]^{p}\times \mathbb {R}$-значные независимые случайные величины, распределенные как пара независимых прототипов $(\mathbf {X} ,Y)$, где $\operatorname {E} [Y^{2}]<\infty$. Мы стремимся предсказать реакцию $Y$, связанный со случайной величиной $\mathbf {X}$, оценивая функцию регрессии $m(\mathbf {x} )=\operatorname {E} [Y\mid \mathbf {X} =\mathbf {x} ]$. Лес случайной регрессии представляет собой ансамбль $M$ деревья рандомизированной регрессии. Обозначим $m_{n}(\mathbf {x} ,\mathbf {\Theta } _{j})$ прогнозируемое значение в точке $\mathbf {x}$ по $j$-е дерево, где $\mathbf {\Theta } _{1},\ldots ,\mathbf {\Theta } _{M}$ являются независимыми случайными величинами, распределенными как общая случайная величина $\mathbf {\Theta }$, независимо от выборки ${\mathcal {D}}_{n}$. Эту случайную величину можно использовать для описания случайности, вызванной разделением узлов и процедурой выборки для построения дерева. Деревья объединяются для формирования оценки конечного леса. $m_{M,n}(\mathbf {x} ,\Theta _{1},\ldots ,\Theta _{M})={\frac {1}{M}}\sum _{j=1}^{M}m_{n}(\mathbf {x} ,\Theta _{j})$. Для деревьев регрессии мы имеем $m_{n}=\sum _{i=1}^{n}{\frac {Y_{i}\mathbf {1} _{\mathbf {X} _{i}\in A_{n}(\mathbf {x} ,\Theta _{j})}}{N_{n}(\mathbf {x} ,\Theta _{j})}}$, где $A_{n}(\mathbf {x} ,\Theta _{j})$ является ячейкой, содержащей $\mathbf {x}$, разработанный со случайностью $\Theta _{j}$ и набор данных ${\mathcal {D}}_{n}$, и $N_{n}(\mathbf {x} ,\Theta _{j})=\sum _{i=1}^{n}\mathbf {1} _{\mathbf {X} _{i}\in A_{n}(\mathbf {x} ,\Theta _{j})}$.

Таким образом, случайные оценки леса удовлетворяют всем $\mathbf {x} \in [0,1]^{d}$, $m_{M,n}(\mathbf {x} ,\Theta _{1},\ldots ,\Theta _{M})={\frac {1}{M}}\sum _{j=1}^{M}\left(\sum _{i=1}^{n}{\frac {Y_{i}\mathbf {1} _{\mathbf {X} _{i}\in A_{n}(\mathbf {x} ,\Theta _{j})}}{N_{n}(\mathbf {x} ,\Theta _{j})}}\right)$. Случайный регрессионный лес имеет два уровня усреднения: сначала по выборкам в целевой ячейке дерева, затем по всем деревьям. Таким образом, вклад наблюдений, находящихся в ячейках с высокой плотностью точек данных, меньше, чем вклад наблюдений, принадлежащих менее населенным ячейкам. Чтобы улучшить методы случайного леса и компенсировать неправильную оценку, Скорнет определил KeRF в $${\tilde {m}}_{M,n}(\mathbf {x} ,\Theta _{1},\ldots ,\Theta _{M})={\frac {1}{\sum _{j=1}^{M}N_{n}(\mathbf {x} ,\Theta _{j})}}\sum _{j=1}^{M}\sum _{i=1}^{n}Y_{i}\mathbf {1} _{\mathbf {X} _{i}\in A_{n}(\mathbf {x} ,\Theta _{j})},$$ что равно среднему значению $Y_{i}$падает в ячейки, содержащие $\mathbf {x}$ в лесу. Если мы определим функцию связи $M$ конечный лес как $K_{M,n}(\mathbf {x} ,\mathbf {z} )={\frac {1}{M}}\sum _{j=1}^{M}\mathbf {1} _{\mathbf {z} \in A_{n}(\mathbf {x} ,\Theta _{j})}$, т.е. доля ячеек, разделенных между $\mathbf {x}$ и $\mathbf {z}$, то почти наверняка имеем ${\tilde {m}}_{M,n}(\mathbf {x} ,\Theta _{1},\ldots ,\Theta _{M})={\frac {\sum _{i=1}^{n}Y_{i}K_{M,n}(\mathbf {x} ,\mathbf {x} _{i})}{\sum _{\ell =1}^{n}K_{M,n}(\mathbf {x} ,\mathbf {x} _{\ell })}}$, который определяет KeRF.

Центрированный KeRF

Построение Центрированного уровня KeRF $k$ то же самое, что и для центрированного леса, за исключением того, что прогнозы делаются ${\tilde {m}}_{M,n}(\mathbf {x} ,\Theta _{1},\ldots ,\Theta _{M})$, соответствующая функция ядра или функция соединения $$K_{k}^{cc}(\mathbf {x} ,\mathbf {z} )=\sum _{k_{1},\ldots ,k_{d},\sum _{j=1}^{d}k_{j}=k}{\frac {k!}{k_{1}!\cdots k_{d}!}}\left({\frac {1}{d}}\right)^{k}\prod _{j=1}^{d}\mathbf {1} _{\lceil 2^{k_{j}}x_{j}\rceil =\lceil 2^{k_{j}}z_{j}\rceil },\qquad {\text{ for all }}\mathbf {x} ,\mathbf {z} \in [0,1]^{d}.$$

Униформа КеРФ

Однородный KeRF строится так же, как и однородный лес, за исключением того, что прогнозы делаются ${\tilde {m}}_{M,n}(\mathbf {x} ,\Theta _{1},\ldots ,\Theta _{M})$, соответствующая функция ядра или функция соединения $$K_{k}^{uf}(\mathbf {0} ,\mathbf {x} )=\sum _{k_{1},\ldots ,k_{d},\sum _{j=1}^{d}k_{j}=k}{\frac {k!}{k_{1}!\ldots k_{d}!}}\left({\frac {1}{d}}\right)^{k}\prod _{m=1}^{d}\left(1-|x_{m}|\sum _{j=0}^{k_{m}-1}{\frac {\left(-\ln |x_{m}|\right)^{j}}{j!}}\right){\text{ for all }}\mathbf {x} \in [0,1]^{d}.$$

Характеристики

Связь между KeRF и случайным лесом

Прогнозы, данные KeRF и случайными лесами, близки, если количество точек в каждой ячейке контролируется:

Предположим, что существуют последовательности $(a_{n}),(b_{n})$ такое, что почти наверняка $$a_{n}\leq N_{n}(\mathbf {x} ,\Theta )\leq b_{n}{\text{ and }}a_{n}\leq {\frac {1}{M}}\sum _{m=1}^{M}N_{n}{\mathbf {x} ,\Theta _{m}}\leq b_{n}.$$ Тогда почти наверняка $$|m_{M,n}(\mathbf {x} )-{\tilde {m}}_{M,n}(\mathbf {x} )|\leq {\frac {b_{n}-a_{n}}{a_{n}}}{\tilde {m}}_{M,n}(\mathbf {x} ).$$

Связь между бесконечным KeRF и бесконечным случайным лесом

Когда количество деревьев $M$ уходит в бесконечность, то мы имеем бесконечный случайный лес и бесконечный KeRF. Их оценки близки, если число наблюдений в каждой ячейке ограничено:

Предположим, что существуют последовательности $(\varepsilon _{n}),(a_{n}),(b_{n})$ такое, что почти наверняка

• $\operatorname {E} [N_{n}(\mathbf {x} ,\Theta )]\geq 1,$
• $\operatorname {P} [a_{n}\leq N_{n}(\mathbf {x} ,\Theta )\leq b_{n}\mid {\mathcal {D}}_{n}]\geq 1-\varepsilon _{n}/2,$
• $\operatorname {P} [a_{n}\leq \operatorname {E} _{\Theta }[N_{n}(\mathbf {x} ,\Theta )]\leq b_{n}\mid {\mathcal {D}}_{n}]\geq 1-\varepsilon _{n}/2,$

Тогда почти наверняка $$|m_{\infty ,n}(\mathbf {x} )-{\tilde {m}}_{\infty ,n}(\mathbf {x} )|\leq {\frac {b_{n}-a_{n}}{a_{n}}}{\tilde {m}}_{\infty ,n}(\mathbf {x} )+n\varepsilon _{n}\left(\max _{1\leq i\leq n}Y_{i}\right).$$

Согласованность результатов

Предположим, что $Y=m(\mathbf {X} )+\varepsilon$, где $\varepsilon$ представляет собой центрированный гауссов шум, не зависящий от $\mathbf {X}$, с конечной дисперсией $\sigma ^{2}<\infty$. Более того, $\mathbf {X}$ равномерно распределен по $[0,1]^{d}$ и $m$ является Липшиц . Скорнет доказал верхние границы скоростей согласованности для центрированного KeRF и однородного KeRF.

Согласованность центрированного KeRF

Предоставление $k\rightarrow \infty$ и $n/2^{k}\rightarrow \infty$, существует константа $C_{1}>0$ такой, что для всех $n$, $\mathbb {E} [{\tilde {m}}_{n}^{cc}(\mathbf {X} )-m(\mathbf {X} )]^{2}\leq C_{1}n^{-1/(3+d\log 2)}(\log n)^{2}$.

Консистенция однородного KeRF

Предоставление $k\rightarrow \infty$ и $n/2^{k}\rightarrow \infty$, существует константа $C>0$ такой, что, $\mathbb {E} [{\tilde {m}}_{n}^{uf}(\mathbf {X} )-m(\mathbf {X} )]^{2}\leq Cn^{-2/(6+3d\log 2)}(\log n)^{2}$.

Недостатки

Хотя случайные леса часто достигают более высокой точности, чем одно дерево решений, они жертвуют внутренней интерпретируемостью, присущей деревьям решений. Деревья решений относятся к довольно небольшому семейству моделей машинного обучения, которые легко интерпретируются наряду с линейными моделями, моделями , основанными на правилах , и моделями, основанными на внимании . Эта интерпретируемость является одним из наиболее желательных качеств деревьев решений. Это позволяет разработчикам подтвердить, что модель извлекла из данных реалистичную информацию, и позволяет конечным пользователям доверять решениям, принимаемым моделью. Например, проследить путь, по которому дерево решений принимает свое решение, довольно тривиально, но проследить пути десятков или сотен деревьев гораздо сложнее. Чтобы добиться как производительности, так и интерпретируемости, некоторые методы сжатия модели позволяют преобразовать случайный лес в минимальное «возрожденное» дерево решений, которое точно воспроизводит одну и ту же функцию принятия решений. Если установлено, что прогностические атрибуты линейно коррелируют с целевой переменной, использование случайного леса может не повысить точность базового обучаемого. Более того, в задачах с несколькими категориальными переменными случайный лес может не повысить точность базового обучаемого.

См. также

• Повышение — метод машинного обучения
• Обучение дереву решений – алгоритм машинного обучения
• Ансамблевое обучение – статистика и техника машинного обучения
• Повышение градиента — техника машинного обучения
• Непараметрическая статистика . Раздел статистики, основанный не только на параметризованных семействах вероятностных распределений. Страницы, отображающие краткие описания целей перенаправления.
• Рандомизированный алгоритм - алгоритм, который использует определенную степень случайности как часть своей логики или процедуры.

Дальнейшее чтение

• Принци А., Поэль Д. (2007). «Случайная мультиклассовая классификация: обобщение случайных лесов на случайные MNL и случайные NB» . Приложения баз данных и экспертных систем . Конспекты лекций по информатике . Том. 4653. с. 349. дои : 10.1007/978-3-540-74469-6_35 . ISBN  978-3-540-74467-2 .
• Дениско Д., Хоффман М.М. (февраль 2018 г.). «Классификация и взаимодействие в случайных лесах» . Труды Национальной академии наук Соединенных Штатов Америки . 115 (8): 1690–1692. Бибкод : 2018PNAS..115.1690D . дои : 10.1073/pnas.1800256115 . ПМЦ   5828645 . ПМИД   29440440 .

Внешние ссылки

• Описание классификатора случайных лесов (сайт Лео Бреймана)
• Лио, Энди и Винер, Мэтью «Классификация и регрессия с помощью randomForest» R News (2002) Vol. 2/3 р. 18 (Обсуждение использования пакета случайного леса для R )