Параллельная кривая

Не путать с параллельным транспортом .

Параллельные кривые графика $y=1.5\sin(x)$ на расстояния $d=0.25,\dots ,1.5$

Два определения параллельной кривой: 1) огибающая семейства равных окружностей, 2) фиксированное нормальное расстояние.

Параллельные кривые круга (красного цвета) тоже являются кругами.

Параллелью называется кривой центром огибающая с семейства равных окружностей на кривой. Он обобщает понятие параллельных (прямых) линий . Ее также можно определить как кривую, точки которой находятся на постоянном нормальном расстоянии от данной кривой. Эти два определения не полностью эквивалентны, поскольку последнее предполагает гладкость , а первое — нет.

В компьютерном проектировании предпочтительный термин для обозначения параллельной кривой — кривая смещения . (В других геометрических контекстах термин «смещение» также может относиться к переводу . ) Кривые смещения важны, например, при с числовым программным управлением обработке , где они описывают, например, форму реза, выполненного круглым режущим инструментом двухкоординатного станка. Форма реза смещена от траектории фрезы на постоянное расстояние в направлении, нормальном к траектории фрезы в каждой точке.

В области 2D- компьютерной графики , известной как векторная графика , (приблизительное) вычисление параллельных кривых включает в себя одну из фундаментальных операций рисования, называемую обводкой, которая обычно применяется к полилиниям или полибезье (которые сами называются путями) в этой области.

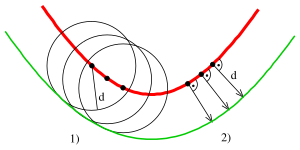
За исключением линии или круга , параллельные кривые имеют более сложную математическую структуру, чем кривая-прародитель. Например, даже если кривая-прародитель гладкая , ее смещения могут быть не такими; это свойство проиллюстрировано на верхнем рисунке с использованием синусоидальной кривой в качестве прародительской кривой. В общем, даже если кривая рациональна , ее смещения могут быть нерациональными. Например, смещения параболы являются рациональными кривыми, но смещения эллипса или гиперболы нерациональны , хотя сами эти кривые-прародители рациональны.

Это понятие также распространяется на трехмерные поверхности , где оно называется поверхностью смещения или параллельной поверхностью . Увеличение твердого объема на (постоянное) расстояние иногда называют расширением . Обратная операция иногда называется обстрелом . Смещенные поверхности важны при с числовым программным управлением обработке , где они описывают форму среза, выполненного сферической концевой фрезой трехосного станка. Другие формы режущих долот можно смоделировать математически с помощью общих поверхностей смещения.

Параллельная кривая параметрически заданной кривой

Если существует регулярное параметрическое представление ${\vec {x}}=(x(t),y(t))$ доступной данной кривой второе определение параллельной кривой (см. выше) приводит к следующему параметрическому представлению параллельной кривой с расстоянием $|d|$:

${\vec {x}}_{d}(t)={\vec {x}}(t)+d{\vec {n}}(t)$ с аппаратом нормально ${\vec {n}}(t)$.

В декартовых координатах:

$x_{d}(t)=x(t)+{\frac {d\;y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}$

$y_{d}(t)=y(t)-{\frac {d\;x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\ .$

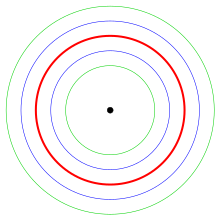
Параметр расстояния $d$ может быть отрицательным. В этом случае на противоположной стороне кривой получается параллельная кривая (см. диаграмму параллельных кривых окружности). Легко проверить, что параллельная кривая прямой является параллельной прямой в обычном смысле, а параллельная кривая окружности — концентрической окружностью.

Геометрические свойства:

• ${\vec {x}}'_{d}(t)\parallel {\vec {x}}'(t),\quad$ это означает: касательные векторы для фиксированного параметра параллельны.
• $k_{d}(t)={\frac {k(t)}{1+dk(t)}},\quad$ с $k(t)$ кривизна и данной кривой $k_{d}(t)$ кривизна параллельной кривой для параметра $t$.
• $R_{d}(t)=R(t)+d,\quad$ с $R(t)$ радиус кривизны данной кривой и $R_{d}(t)$ радиус кривизны параллельной кривой для параметра $t$.
• Когда они существуют, окружности, соприкасающиеся с параллельными кривыми в соответствующих точках, концентричны.
• Что касается параллельных линий , то нормальная линия к кривой также нормальна к ее параллелям.
• Когда строятся параллельные кривые, они будут иметь точки пересечения , когда расстояние от кривой соответствует радиусу кривизны . Это точки, в которых кривая касается эволюты .
• Если кривая-прародитель является границей плоского множества и ее параллельная кривая не имеет самопересечений, то последняя является границей суммы Минковского плоского множества и диска заданного радиуса.

Если данная кривая является полиномиальной (это означает, что $x(t)$ и $y(t)$ являются полиномами), то параллельные кривые обычно не являются полиномами. В области САПР это является недостатком, поскольку системы САПР используют полиномы или рациональные кривые. Чтобы получить хотя бы рациональные кривые, квадратный корень из представления параллельной кривой должен быть разрешимым. Такие кривые называются кривыми годографа Пифагора и были исследованы Р. Т. Фаруки.

Параллельные кривые неявной кривой

Параллельные кривые неявной кривой (красный) с уравнением $x^{4}+y^{4}-1=0$

Обычно аналитическое представление параллельной кривой неявной кривой невозможно. Только для простых случаев прямых и окружностей можно легко описать параллельные кривые.Например:

Линия $\;f(x,y)=x+y-1=0\;$ → функция расстояния: $\;h(x,y)={\frac {x+y-1}{\sqrt {2}}}=d\;$ (нормальная форма Гессена)

Круг $\;f(x,y)=x^{2}+y^{2}-1=0\;$ → функция расстояния: $\;h(x,y)={\sqrt {x^{2}+y^{2}}}-1=d\;.$

В общем случае, при определенных условиях, можно доказать существование ориентированной функции расстояния $h(x,y)$. На практике приходится рассматривать это численно. При рассмотрении параллельных кривых справедливо следующее:

• Параллельная кривая для расстояния d — это набор уровней. $h(x,y)=d$ соответствующей функции ориентированного расстояния $h$.

Свойства функции расстояния:

• $|\operatorname {grad} h({\vec {x}})|=1\;,$
• $h({\vec {x}}+d\operatorname {grad} h({\vec {x}}))=h({\vec {x}})+d\;,$
• $\operatorname {grad} h({\vec {x}}+d\operatorname {grad} h({\vec {x}}))=\operatorname {grad} h({\vec {x}})\;.$

Пример:
На диаграмме показаны параллельные кривые неявной кривой с уравнением $\;f(x,y)=x^{4}+y^{4}-1=0\;.$
Примечание: Кривые $\;f(x,y)=x^{4}+y^{4}-1=d\;$ не являются параллельными кривыми, поскольку $\;|\operatorname {grad} f(x,y)|=1\;$ неверно в интересующей области.

Дальнейшие примеры

Эвольвенты круга

• Эвольвенты данной кривой представляют собой совокупность параллельных кривых. Например: развертки круга представляют собой параллельные спирали (см. схему).

И:

• Парабола 6 - имеет (двусторонние) смещения рациональных кривых й степени.
• Гипербола эллипс или степени имеет (двусторонние) смещения алгебраической кривой 8.
• Кривая Безье степени n имеет (двусторонние) смещения алгебраических кривых степени 4 n − 2 . В частности, кубическая кривая Безье имеет (двусторонние) смещения алгебраических кривых степени 10.

Параллельная кривая кривой с углом

Параллельные кривые кривой с прерывистой нормалью вокруг угла

При определении траектории резания детали с острым углом для обработки необходимо определить кривую, параллельную (смещенную) данной кривой, которая имеет прерывистую нормаль в углу. Даже если данная кривая не является гладкой в ​​остром углу, ее параллельная кривая может быть гладкой с непрерывной нормалью или может иметь изломы , когда расстояние от кривой соответствует радиусу кривизны в остром углу.

Обычные фанаты

Как описано выше , параметрическое представление параллельной кривой, ${\vec {x}}_{d}(t)$, к данной кривой, ${\vec {x}}(t)$, с расстоянием $|d|$ является:

${\vec {x}}_{d}(t)={\vec {x}}(t)+d{\vec {n}}(t)$ с аппаратом нормально ${\vec {n}}(t)$.

В остром углу( $t=t_{c}$), нормальный для ${\vec {x}}(t_{c})$ данный ${\vec {n}}(t_{c})$ разрывен, что означает односторонний предел нормали слева ${\vec {n}}(t_{c}^{-})$ не равно пределу справа ${\vec {n}}(t_{c}^{+})$. Математически,

${\vec {n}}(t_{c}^{-})=\lim _{t\to t_{c}^{-}}{\vec {n}}(t)\neq {\vec {n}}(t_{c}^{+})=\lim _{t\to t_{c}^{+}}{\vec {n}}(t)$.

Обычный веер для определения параллельных кривых вокруг острого угла.

Однако мы можем определить обычный вентилятор ${\vec {n}}_{f}(\alpha )$ который обеспечивает интерполянт между ${\vec {n}}(t_{c}^{-})$ и ${\vec {n}}(t_{c}^{+})$и использовать ${\vec {n}}_{f}(\alpha )$ вместо ${\vec {n}}(t_{c})$ в остром углу:

${\vec {n}}_{f}(\alpha )={\frac {(1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec {n}}(t_{c}^{+})}{\lVert (1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec {n}}(t_{c}^{+})\rVert }},\quad$где $0<\alpha <1$.

Полученное определение параллельной кривой ${\vec {x}}_{d}(t)$ обеспечивает желаемое поведение:

${\vec {x}}_{d}(t)={\begin{cases}{\vec {x}}(t)+d{\vec {n}}(t),&{\text{if }}t<t_{c}{\text{ or }}t>t_{c}\\{\vec {x}}(t_{c})+d{\vec {n}}_{f}(\alpha ),&{\text{if }}t=t_{c}{\text{ where }}0<\alpha <1\end{cases}}$

Алгоритмы

В общем, параллельная кривая кривой Безье не является другой кривой Безье, и этот результат был доказан Тиллером и Хэнсоном в 1984 году. Таким образом, на практике используются методы аппроксимации. Любой желаемый уровень точности возможен путем многократного деления кривой, хотя более эффективные методы требуют меньшего количества делений для достижения того же уровня точности. Опрос Элбера, Ли и Кима 1997 года. широко цитируется, хотя в последнее время были предложены более эффективные методы. Современная методика, основанная на подгонке кривой , со ссылками и сравнениями с другими алгоритмами, а также исходным кодом JavaScript с открытым исходным кодом, была опубликована в сообщении в блоге. в сентябре 2022 года.

Другим эффективным алгоритмом компенсации является подход уровня, описанный Киммел и Брукштейн (1993).

Параллельные (смещенные) поверхности

Офсетная поверхность сложной неправильной формы

Смещенные поверхности важны при с числовым программным управлением обработке , где они описывают форму среза, выполненного сферической концевой фрезой трехосной фрезы. Если существует регулярное параметрическое представление ${\vec {x}}(u,v)=(x(u,v),y(u,v),z(u,v))$ доступной данной поверхности второе определение параллельной кривой (см. выше) обобщается до следующего параметрического представления параллельной поверхности с расстоянием $|d|$:

${\vec {x}}_{d}(u,v)={\vec {x}}(u,v)+d{\vec {n}}(u,v)$ с аппаратом нормально ${\vec {n}}_{d}(u,v)={{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}} \over {|{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}}|}}$.

Параметр расстояния $d$ может быть и отрицательным. В этом случае на противоположной стороне поверхности получается параллельная поверхность (см. аналогичную диаграмму на параллельных кривых окружности). Легко проверяется: параллельная поверхность плоскости — это параллельная плоскость в обычном смысле, а параллельная поверхность сферы — это концентрическая сфера.

Геометрические свойства:

• ${\partial {\vec {x}}_{d} \over \partial u}\parallel {\partial {\vec {x}} \over \partial u},\quad {\partial {\vec {x}}_{d} \over \partial v}\parallel {\partial {\vec {x}} \over \partial v},\quad$ это означает: касательные векторы для фиксированных параметров параллельны.
• ${\vec {n}}_{d}(u,v)=\pm {\vec {n}}(u,v),\quad$ это означает: векторы нормалей для фиксированных параметров совпадают по направлению.
• $S_{d}=(1+dS)^{-1}S,\quad$ где $S_{d}$ и $S$ являются операторами формы для ${\vec {x}}_{d}$ и ${\vec {x}}$, соответственно.

Главные кривизны являются собственными значениями оператора формы , главные направления кривизны — его собственными векторами , гауссова кривизна — его определителем , а средняя кривизна — половиной его следа .

• $S_{d}^{-1}=S^{-1}+dI,\quad$ где $S_{d}^{-1}$ и $S^{-1}$ являются обратными операторами формы для ${\vec {x}}_{d}$ и ${\vec {x}}$, соответственно.

Главные радиусы кривизны — собственные значения обратного оператора формы , главные направления кривизны — его собственные векторы , обратная гауссовой кривизне — ее определитель , а средний радиус кривизны — половина ее следа .

Обратите внимание на сходство геометрических свойств параллельных кривых .

Обобщения

Проблема довольно очевидно распространяется на более высокие измерения, например, на смещенные поверхности, и несколько менее тривиально на поверхности труб . Обратите внимание, что терминология для многомерных версий варьируется еще шире, чем для плоского случая, например, другие авторы говорят о параллельных волокнах, лентах и ​​трубках. Для кривых, встроенных в 3D-поверхности, смещение может быть взято вдоль геодезической .

Другой способ обобщить это (даже в 2D) рассмотреть переменное расстояние, например, параметризованное другой кривой. Например, можно обвести (конверт) эллипсом вместо круга. как это возможно например в METAFONT .

Огибающая эллипсов, образующая две общие кривые смещения выше и ниже заданной кривой.

Совсем недавно Adobe Illustrator добавил нечто подобное в версию CS5 , хотя контрольные точки для переменной ширины указаны визуально. В контекстах, где важно различать постоянное и переменное смещение расстояния, иногда используются аббревиатуры CDO и VDO.

Общие кривые смещения

Предположим, у вас есть регулярное параметрическое представление кривой: ${\vec {x}}(t)=(x(t),y(t))$, и у вас есть вторая кривая, которую можно параметризовать с помощью ее единичной нормали, ${\vec {d}}({\vec {n}})$, где нормаль ${\vec {d}}({\vec {n}})={\vec {n}}$ (эта параметризация нормалью существует для кривых, кривизна которых строго положительная или отрицательная и, следовательно, выпуклая, гладкая, а не прямая). Параметрическое представление общей кривой смещения ${\vec {x}}(t)$ компенсируется ${\vec {d}}({\vec {n}})$ является:

${\vec {x}}_{d}(t)={\vec {x}}(t)+{\vec {d}}({\vec {n}}(t)),\quad$ где ${\vec {n}}(t)$ является единичной нормой ${\vec {x}}(t)$.

Обратите внимание, что тривиальное смещение, ${\vec {d}}({\vec {n}})=d{\vec {n}}$, дает вам обычные параллельные (или смещенные) кривые.

Геометрические свойства:

• ${\vec {x}}'_{d}(t)\parallel {\vec {x}}'(t),\quad$ это означает: касательные векторы для фиксированного параметра параллельны.
• Что касается параллельных линий , нормаль к кривой также является нормалью к ее общим смещениям.
• $k_{d}(t)={\dfrac {k(t)}{1+{\dfrac {k(t)}{k_{n}(t)}}}},\quad$ с $k_{d}(t)$ кривизна , общей кривой смещения $k(t)$ кривизна ${\vec {x}}(t)$, и $k_{n}(t)$ кривизна ${\vec {d}}({\vec {n}}(t))$ для параметра $t$.
• $R_{d}(t)=R(t)+R_{n}(t),\quad$ с $R_{d}(t)$ радиус кривизны общей кривой смещения, $R(t)$ радиус кривизны ${\vec {x}}(t)$, и $R_{n}(t)$ радиус кривизны ${\vec {d}}({\vec {n}}(t))$ для параметра $t$.
• Когда строятся общие кривые смещения, они будут иметь перегибы , когда кривизна кривой соответствует кривизне смещения. Это точки, в которых кривая касается эволюты .

Общие смещенные поверхности

Общие поверхности смещения описывают форму резов, выполняемых различными режущими головками, используемыми трехосными концевыми фрезами при с числовым программным управлением обработке . Предположим, у вас есть регулярное параметрическое представление поверхности. ${\vec {x}}(u,v)=(x(u,v),y(u,v),z(u,v))$, и у вас есть вторая поверхность, которую можно параметризовать ее единицей нормали, ${\vec {d}}({\vec {n}})$, где нормаль ${\vec {d}}({\vec {n}})={\vec {n}}$ (эта параметризация нормалью существует для поверхностей, гауссова кривизна которых строго положительна и, следовательно, выпукла, гладка, а не плоская). Параметрическое представление общей поверхности смещения ${\vec {x}}(t)$ компенсируется ${\vec {d}}({\vec {n}})$ является:

${\vec {x}}_{d}(u,v)={\vec {x}}(u,v)+{\vec {d}}({\vec {n}}(u,v)),\quad$ где ${\vec {n}}(u,v)$ является единичной нормой ${\vec {x}}(u,v)$.

Обратите внимание, что тривиальное смещение, ${\vec {d}}({\vec {n}})=d{\vec {n}}$, дает вам обычные параллельные (или смещенные) поверхности.

Геометрические свойства:

• Что касается параллельных линий , касательная плоскость поверхности параллельна касательной плоскости ее общих смещений.
• Что касается параллельных линий , нормаль к поверхности также является нормалью к ее общим смещениям.
• $S_{d}=(1+SS_{n}^{-1})^{-1}S,\quad$ где $S_{d},S,$ и $S_{n}$ являются операторами формы для ${\vec {x}}_{d},{\vec {x}},$ и ${\vec {d}}({\vec {n}})$, соответственно.

Главные кривизны являются собственными значениями оператора формы , главные направления кривизны — его собственными векторами , гауссова кривизна — его определителем , а средняя кривизна — половиной его следа .

• $S_{d}^{-1}=S^{-1}+S_{n}^{-1},\quad$ где $S_{d}^{-1},S^{-1}$ и $S_{n}^{-1}$ являются обратными операторами формы для ${\vec {x}}_{d},{\vec {x}},$ и ${\vec {d}}({\vec {n}})$, соответственно.

Главные радиусы кривизны — собственные значения обратного оператора формы , главные направления кривизны — его собственные векторы , обратная гауссовой кривизне — ее определитель , а средний радиус кривизны — половина ее следа .

Обратите внимание на сходство геометрических свойств обычных кривых смещения .

Вывод геометрических свойств для общих смещений

Геометрические свойства, перечисленные выше для общих кривых и поверхностей смещения, могут быть получены для смещений произвольного размера. Предположим, у вас есть регулярное параметрическое представление n-мерной поверхности: ${\vec {x}}({\vec {u}})$, где размерность ${\vec {u}}$ является n-1. Также предположим, что у вас есть вторая n-мерная поверхность, которую можно параметризовать ее единичной нормалью, ${\vec {d}}({\vec {n}})$, где нормаль ${\vec {d}}({\vec {n}})={\vec {n}}$ (эта параметризация нормалью существует для поверхностей, гауссова кривизна которых строго положительна и, следовательно, выпукла, гладка, а не плоская). Параметрическое представление общей поверхности смещения ${\vec {x}}({\vec {u}})$ компенсируется ${\vec {d}}({\vec {n}})$ является:

${\vec {x}}_{d}({\vec {u}})={\vec {x}}({\vec {u}})+{\vec {d}}({\vec {n}}({\vec {u}})),\quad$ где ${\vec {n}}({\vec {u}})$ является единичной нормой ${\vec {x}}({\vec {u}})$. (Тривиальное смещение, ${\vec {d}}({\vec {n}})=d{\vec {n}}$, дает вам обычные параллельные поверхности.)

Во-первых, обратите внимание, что норма ${\vec {x}}({\vec {u}})=$ нормальный из ${\vec {d}}({\vec {n}}({\vec {u}}))={\vec {n}}({\vec {u}}),$ по определению. Теперь мы применим дифференциал относительно ${\vec {u}}$ к ${\vec {x}}_{d}$, что дает нам касательные векторы, охватывающие его касательную плоскость.

$\partial {\vec {x}}_{d}({\vec {u}})=\partial {\vec {x}}({\vec {u}})+\partial {\vec {d}}({\vec {n}}({\vec {u}}))$

Обратите внимание, что касательные векторы для ${\vec {x}}_{d}$ представляют собой сумму касательных векторов для ${\vec {x}}({\vec {u}})$ и его смещение ${\vec {d}}({\vec {n}})$, которые имеют одну и ту же единицу измерения. Таким образом, общая поверхность смещения имеет одну и ту же касательную плоскость и нормаль к ${\vec {x}}({\vec {u}})$ и ${\vec {d}}({\vec {n}}({\vec {u}}))$. Это соответствует природе конвертов.

Теперь рассмотрим уравнения Вайнгартена для оператора формы , которые можно записать в виде $\partial {\vec {n}}=-\partial {\vec {x}}S$. Если $S$ является обратимым, $\partial {\vec {x}}=-\partial {\vec {n}}S^{-1}$. Напомним, что главные кривизны поверхности — это собственные значения оператора формы, главные направления кривизны — её собственные векторы , кривизна Гаусса — её определитель , а средняя кривизна — половина её следа . Обратный оператор формы сохраняет те же значения для радиусов кривизны.

Подставив в уравнение дифференциал ${\vec {x}}_{d}$, мы получаем:

$\partial {\vec {x}}_{d}=\partial {\vec {x}}-\partial {\vec {n}}S_{n}^{-1},\quad$ где $S_{n}$ является оператором формы для ${\vec {d}}({\vec {n}}({\vec {u}}))$.

Далее мы снова используем уравнения Вайнгартена для замены $\partial {\vec {n}}$:

$\partial {\vec {x}}_{d}=\partial {\vec {x}}+\partial {\vec {x}}SS_{n}^{-1},\quad$ где $S$ является оператором формы для ${\vec {x}}({\vec {u}})$.

Затем решаем для $\partial {\vec {x}}$ и умножить обе стороны на $-S$ чтобы вернуться к уравнениям Вайнгартена , на этот раз для $\partial {\vec {x}}_{d}$:

$\partial {\vec {x}}_{d}(I+SS_{n}^{-1})^{-1}=\partial {\vec {x}},$

$-\partial {\vec {x}}_{d}(I+SS_{n}^{-1})^{-1}S=-\partial {\vec {x}}S=\partial {\vec {n}}.$

Таким образом, $S_{d}=(I+SS_{n}^{-1})^{-1}S$, и инвертирование обеих сторон дает нам: $S_{d}^{-1}=S^{-1}+S_{n}^{-1}$.

См. также

• Отображение рельефа
• Функция расстояния и функция расстояния со знаком
• Поле расстояния
• Офсетная печать
• Трубчатый район

Ссылки

• Йозеф Хошек: Смещение кривых на плоскости. В: CAD. 17 (1985), С. 77–81.
• Такаси Маэкава: Обзор смещенных кривых и поверхностей. В: CAD. 31 (1999), С. 165–173.

Дальнейшее чтение

• Фаруки, RT; Нефф, Калифорния (1990). «Аналитические свойства кривых смещения плоскости». Компьютерное геометрическое проектирование . 7 (1–4): 83–99. дои : 10.1016/0167-8396(90)90023-К .
• Пигл, Лес А. (1999). «Вычисление смещений кривых и поверхностей NURBS». Компьютерное проектирование . 31 (2): 147–156. CiteSeerX   10.1.1.360.2793 . дои : 10.1016/S0010-4485(98)00066-9 .
• Портеус, Ян Р. (2001). Геометрическая дифференциация: для интеллекта кривых и поверхностей (2-е изд.). Издательство Кембриджского университета. стр. 1–25. ISBN  978-0-521-00264-6 .
• Патрикалакис, Николас М.; Маэкава, Такаши (2010) [2002]. Опрос формы для автоматизированного проектирования и производства . Springer Science & Business Media. Глава 11. Кривые смещения и поверхности. ISBN  978-3-642-04074-0 . Бесплатная онлайн-версия .
• Антон, Франсуа; Эмирис, Иоаннис З.; Муррен, Бернар; Тейо, Моник (май 2005 г.). «Набор O для алгебраической кривой и приложение к коникам». Международная конференция по вычислительной науке и ее приложениям . Сингапур: Springer Verlag. стр. 683–696.
• Фаруки, Рида Т. (2008). Кривые годографа Пифагора: алгебра и геометрия неразделимы . Springer Science & Business Media. стр. 141–178. ISBN  978-3-540-73397-3 . Перечисленные страницы представляют собой общий и вводный материал.
• Ау, СК; Ма, Ю.-С. (2013). «Расчет кривых смещения с использованием функции расстояния: решение ключевой проблемы при создании траектории режущего инструмента». В Ма, Ю.-С. (ред.). Семантическое моделирование и совместимость в разработке продуктов и процессов: технология инженерной информатики . Springer Science & Business Media. стр. 259–273. ISBN  978-1-4471-5073-2 .

Внешние ссылки

• Параллельные кривые в MathWorld
• Визуальный словарь плоских кривых Кса Ли
• http://library.imageworks.com/pdfs/imageworks-library-offset-curve-deformation-from-Skeletal-Anima.pdf приложение к анимации; запатентован как патент США 8 400 455
• http://www2.uah.es/fsegundo/Otros/Offset/16-SanSegundoSendraSendra-1532.pdf