Правильный косой многогранник

В геометрии правильные косые многогранники являются обобщениями набора правильных многогранников , которые включают возможность неплоских граней или вершинных фигур . Коксетер изучал косые вершинные фигуры, которые создавали новые четырехмерные правильные многогранники, а намного позже Бранко Грюнбаум изучал правильные косые грани. ^{[ 1 ]}

Бесконечные правильные косые многогранники, охватывающие 3-мерное пространство или выше, называются правильными косыми апейроэдрами .

История

По мнению Коксетера , в 1926 году Джон Флиндерс Петри обобщил понятие правильных косых многоугольников (неплоских многоугольников) на правильные косые многогранники .

Коксетер предложил модифицированный символ Шлефли ${l, m | n}$ для этих фигур, где ${l, m}$ подразумевает фигуру вершины , $m$ $l$ -угольники вокруг вершины и $n$ -угольные отверстия. Их вершинные фигуры представляют собой косые многоугольники , зигзагообразные между двумя плоскостями.

Правильные косые многогранники, представленные ${l, m | n}$ , следуйте этому уравнению:

2\cos {\frac {\pi }{l}}\cos {\frac {\pi }{m}}=\cos {\frac {\pi }{n}}

Первый набор ${l, m | n}$ повторяет пять выпуклых платоновых тел и одно невыпуклое тело Кеплера – Пуансо :

${л, м \|} п$	Лица	Края	Вершины	$п$	Многогранник	Симметрия заказ
{3,3\| 3} = {3,3}	4	6	4	0	Тетраэдр	12
{3,4\| 4} = {3,4}	8	12	6	0	Октаэдр	24
{4,3\| 4} = {4,3}	6	12	8	0	Куб	24
{3,5\| 5} = {3,5}	20	30	12	0	Икосаэдр	60
{5,3\| 5} = {5,3}	12	30	20	0	Додекаэдр	60
{5,5\| 3} = {5,5/2}	12	30	12	4	Большой додекаэдр	60

Конечные правильные косые многогранники

А4 плоскости Кокстера Проекции

${4, 6 \| 3}$	${6, 4 \| 3}$
Ранцинированный 5-клеточный (20 вершин, 60 ребер)	Усеченный 5-ячеечный (30 вершин, 60 ребер)
F4 Проекции плоскости Кокстера

${4, 8 \| 3}$	${8, 4 \| 3}$
Ранцинированный 24-клеточный (144 вершины, 576 ребер)	Усеченный 24-ячеечный (288 вершин, 576 ребер)

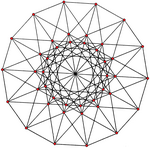
${3,8\|,4} = {3,8} 8$	${4,6\|,3} = {4,6} 6$
42 вершины, 168 ребер	56 вершин, 168 ребер
Некоторые из 4-мерных правильных косых многогранников помещаются внутри однородной многохоры, как показано в четырех верхних проекциях.

Коксетер также перечислил более широкий набор конечных правильных многогранников в своей статье «Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги».

Точно так же, как бесконечные косые многогранники представляют поверхности многообразия между ячейками выпуклых однородных сот , все конечные формы представляют поверхности многообразия внутри ячеек однородных 4-многогранников .

Многогранники вида {2p, 2q | r} связаны с группы Кокстера симметрией [(p,r,q,r)], которая сводится к линейному [r,p,r], когда q равно 2. Коксетер определяет эту симметрию как [[( p , r , д , р )] ⁺] которая, по его словам, изоморфна его абстрактной группе (2 p ,2 q |2, r ). Соответствующие соты имеют расширенную симметрию [[( p , r , q , r )]]. ^{[ 2 ]}

{2p,4|r} представлен гранями {2p} усеченного { r,p,r} однородного 4-многогранника , а {4,2p|r} представлен квадратными гранями усеченного { r,p ,р}.

{4,4|n} создает n - n дуопризму , и, в частности, {4,4|4} помещается внутри тессеракта {4}x{4} .

{4,4\| n} решения представляют собой квадратные грани дуопризм с n-угольными гранями в виде отверстий и представляют собой тор Клиффорда , а также приближение дуоцилиндра	6,6 {4,4\|6} имеет 36 квадратных граней, которые в перспективной проекции рассматриваются как квадраты, извлеченные из дуопризмы .	{4,4\|4} имеет 16 квадратных граней и существует как подмножество граней в тессеракте .

Конечные многогранники в 4 измерениях
{л, м \| п}	Лица	Края	Вершины	п	Структура	Симметрия	Заказ	Родственная равномерная полихора
{4,4\| 3}	9	18	9	1	Д ₃ х Д ₃	[[3,2,3] ⁺]	9	3-3 дуопризма
{4,4\| 4}	16	32	16	1	Д ₄ х Д ₄	[[4,2,4] ⁺]	16	4-4 дуопризма или тессеракт
{4,4\| 5}	25	50	25	1	Д ₅ х Д ₅	[[5,2,5] ⁺]	25	5-5 дуопризма
{4,4\| 6}	36	72	36	1	Д ₆ х Д ₆	[[6,2,6] ⁺]	36	6-6 дуопризма
{4,4\| п}	н ²	2н ²	н ²	1	Д _н хД _н	[[n,2,n] ⁺]	н ²	nn дуопризма
{4,6\| 3}	30	60	20	6	С5	[[3,3,3] ⁺]	60	Ранцинированный 5-клеточный
{6,4\| 3}	20	60	30	6	С5	[[3,3,3] ⁺]	60	Усеченный 5-ячеечный
{4,8\| 3}	288	576	144	73		[[3,4,3] ⁺]	576	Ранцинированный 24-клеточный
{8,4\| 3}	144	576	288	73		[[3,4,3] ⁺]	576	Усеченный 24-ячеечный

пентаграмматические решения
{л, м \| п}	Лица	Края	Вершины	п	Структура	Симметрия	Заказ	Родственная равномерная полихора
{4,5\| 5}	90	180	72	10	А6	[[5/2,5,5/2] ⁺]	360	Сморщенный большой звездчатый 120-клеточный
{5,4\| 5}	72	180	90	10	А6	[[5/2,5,5/2] ⁺]	360	Усеченный большой звездчатый 120-ячеечный

{л, м \| п}	Лица	Края	Вершины	п	Структура	Заказ	Связанные однородные многогранники
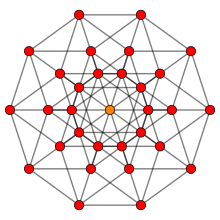
{4,5\| 4}	40	80	32	5	?	160	Вершины 5-куба (±1,±1,±1,±1,±1) и ребра
{5,4\| 4}	32	80	40	5	?	160	Выпрямленные 5-ортоплексные вершины (±1,±1,0,0,0)
{4,7\| 3}	42	84	24	10	НЧ(2,7)	168
{7,4\| 3}	24	84	42	10	НЧ(2,7)	168
{5,5\| 4}	72	180	72	19	А6	360
{6,7\| 3}	182	546	156	105	НЧ(2,13)	1092
{7,6\| 3}	156	546	182	105	НЧ(2,13)	1092
{7,7\| 3}	156	546	156	118	НЧ(2,13)	1092
{4,9\| 3}	612	1224	272	171	НЧ(2,17)	2448
{9,4\| 3}	272	1224	612	171	НЧ(2,17)	2448
{7,8\| 3}	1536	5376	1344	1249	?	10752
{8,7\| 3}	1344	5376	1536	1249	?	10752

Окончательный набор основан на дальнейшей расширенной форме Кокстера {q1,m|q2,q3...} или с неуказанным q2: {l, m |, q}. Их также можно представить в виде регулярного конечного отображения или { l , m } _{2 q} и группы G ^{л , м , q}. ^{[ 3 ]}

{ л , м \|, q } или { л , м } _{2 q}	Лица	Края	Вершины	п	Структура	Заказ	Связанные сложные многогранники
{3,6\|, q } = {3,6} _{2 q}	2 кв. ²	33кв ²	д ²	1	Г ^{3,6,2 ц}	2 кв. ²
{3,2 q \|,3} = {3,2 q } ₆	2кв. ²	3кв. ²	3кв.	( q -1)*( q -2)/2	Г ^{3,6,2 ц}	2 кв. ²
{3,7\|,4} = {3,7} ₈	56	84	24	3	НЧ(2,7)	168
{3,8\|,4} = {3,8} ₈	112	168	42	8	ПГЛ(2,7)	336	(1 1 1 ₁⁴) ⁴,
{4,6\|,3} = {4,6} ₆	84	168	56	15	ПГЛ(2,7)	336	(1 ⁴ 1 ⁴ 1 ₁) ⁽³⁾,
{3,7\|,6} = {3,7} ₁₂	364	546	156	14	НЧ(2,13)	1092
{3,7\|,7} = {3,7} ₁₄	364	546	156	14	НЧ(2,13)	1092
{3,8\|,5} = {3,8} ₁₀	720	1080	270	46	Г ^3,8,10	2160	(1 1 1 ₁⁴) ⁵,
{3,10\|,4} = {3,10} ₈	720	1080	216	73	Г ^3,8,10	2160	(1 1 1 ₁⁵) ⁴,
{4,6\|,2} = {4,6} ₄	12	24	8	3	S4 ×S2	48
{5,6\|,2} = {5,6} ₄	24	60	20	9	A5 ×S2	120
{3,11\|,4} = {3,11} ₈	2024	3036	552	231	НЧ(2,23)	6072
{3,7\|,8} = {3,7} ₁₆	3584	5376	1536	129	Г ^3,7,17	10752
{3,9\|,5} = {3,9} ₁₀	12180	18270	4060	1016	ЛФ(2,29)×А3	36540

Высшие измерения

Правильные косые многогранники также можно построить в размерностях больше 4 как вложения в правильные многогранники или соты. Например, правильный икосаэдр можно вложить в вершины 6-демикуба ; назвал его косым икосаэдром Коксетер правильным . Додекаэдр аналогичным образом можно встроить в 10-демикуб . ^{[ 4 ]}

См. также

Примечания

^ Абстрактные правильные многогранники, стр.7, стр.17
^ Коксетер, Правильные и полуправильные многогранники II 2.34)
^ Коксетер и Мозер, Генераторы и отношения для дискретных групп, раздел 8.6. Карты с указанием многоугольников Петри. п. 110
^ Деза, Майкл; Штогрин, Михаил (1998). «Вложение графов правильных мозаик и звездочек-сот в графы гиперкубов и кубических решеток» . Продвинутые исследования в области чистой математики . Договоренности – Токио 1998: 77. doi : 10.2969/aspm/02710073 . ISBN 978-4-931469-77-8 . Проверено 4 апреля 2020 г.

Ссылки

Питер МакМаллен, Четырехмерные правильные многогранники , дискретная и вычислительная геометрия, сентябрь 2007 г., том 38, выпуск 2, стр. 355–387.
Коксетер , Правильные многогранники , Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 2) HSM Coxeter, «Правильные губки, или косые многогранники», Scripta Mathematica 6 (1939) 240–244.
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559–591]
Коксетер , Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN 0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги, Труды Лондонского математического общества, Сер. 2, Том 43, 1937.)
- Коксетер, HSM Правильные косые многогранники в трех и четырех измерениях. Учеб. Лондонская математика. Соц. 43, 33–62, 1937.
Гарнер, Правильные косые многогранники CWL в гиперболическом трехмерном пространстве. Может. Дж. Математика. 19, 1179–1186, 1967.
Э. Шульте, Дж. М. Уиллс о правильных косых многогранниках Коксетера , Дискретная математика, том 60, июнь – июль 1986 г., страницы 253–262

[1] Абстрактные правильные многогранники, стр.7, стр.17

[2] Коксетер, Правильные и полуправильные многогранники II 2.34)

[3] Коксетер и Мозер, Генераторы и отношения для дискретных групп, раздел 8.6. Карты с указанием многоугольников Петри. п. 110

[4] Деза, Майкл; Штогрин, Михаил (1998). «Вложение графов правильных мозаик и звездочек-сот в графы гиперкубов и кубических решеток» . Продвинутые исследования в области чистой математики . Договоренности – Токио 1998: 77. doi : 10.2969/aspm/02710073 . ISBN 978-4-931469-77-8 . Проверено 4 апреля 2020 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]