Кинетический анализ хода реакции
В химии кинетический анализ хода реакции ( RPKA ) представляет собой подмножество широкого спектра кинетических методов, используемых для определения законов скорости химических реакций и для помощи в выяснении механизмов реакции . Хотя концепции, лежащие в основе кинетического анализа хода реакции, не новы, этот процесс был формализован профессором Донной Блэкмонд (в настоящее время работает в Исследовательском институте Скриппса ) в конце 1990-х годов и с тех пор находит все более широкое применение. В отличие от более распространенного анализа псевдопервого порядка , в котором используется подавляющий избыток одного или нескольких реагентов по отношению к интересующему виду, RPKA исследует реакции в синтетически значимых условиях (т.е. с концентрациями и соотношениями реагентов, напоминающими те, которые используются в реакции, когда не исследуя закон скорости.) Как правило, этот анализ включает систему, в которой концентрации нескольких реагентов заметно изменяются в ходе реакции. Поскольку механизм может меняться в зависимости от относительной и абсолютной концентрации Для задействованных видов этот подход дает результаты, которые гораздо более репрезентативны для реакционного поведения в обычно используемых условиях, чем традиционная тактика. Кроме того, информация, полученная путем наблюдения за реакцией с течением времени, может дать представление о неожиданном поведении, таком как периоды индукции, дезактивация катализатора или изменения в механизме. [1] [2]
Мониторинг хода реакции
[ редактировать ]Кинетический анализ хода реакции основан на способности точно отслеживать конверсию реакции с течением времени. Эта цель может быть достигнута с помощью ряда методов, наиболее распространенные из которых описаны ниже. Хотя эти методы иногда классифицируются как дифференциальные (мониторинг скорости реакции с течением времени) или интегральные (мониторинг количества субстрата и/или продукта с течением времени), простые математические манипуляции ( дифференциация или интеграция ) позволяют осуществлять взаимное преобразование данных, полученных любым из двух методов. . Независимо от реализованного метода, как правило, выгодно подтвердить достоверность в интересующей системе путем мониторинга с помощью дополнительного независимого метода. [2]
Ход реакции ЯМР
[ редактировать ]ЯМР- спектроскопия часто является методом выбора для мониторинга хода реакции, когда расход субстрата и/или образование продукта можно наблюдать с течением времени по изменению интегрирования пика относительно нереакционноспособного стандарта. Из данных о концентрации скорость реакции во времени можно получить, взяв производную полиномиальной аппроксимации экспериментальной кривой. [3] ЯМР хода реакции можно классифицировать как интегральный метод, поскольку собранные первичные данные пропорциональны концентрации и времени. [2] Хотя этот метод чрезвычайно удобен для четко определенных систем с характерными, изолированными пиками продуктов и/или реагентов, у него есть недостаток: требуется гомогенная система, поддающаяся реакции в пробирке ЯМР. Хотя ЯМР-наблюдение может позволить идентифицировать промежуточные продукты реакции, присутствие какого-либо конкретного вещества в ходе реакции не обязательно означает его участие в продуктивном процессе. [1] Однако ход реакции ЯМР часто можно проводить при переменной температуре, что позволяет регулировать скорость реакции до уровня, удобного для наблюдения. Примеров использования ЯМР прогресса реакции имеется множество, причем примечательные примеры включают исследование аминирования Бухвальда-Хартвига (можно отметить, что серьезные дебаты окружали лучший подход к механистическому развитию аминирования Бухвальда-Хартвига, о чем свидетельствует ряд противоречивых и конкурирующих опубликованных отчетов). в течение короткого периода времени. См. указанную статью и ссылки в ней.) [4]
на месте ИК-Фурье
[ редактировать ]in situ Инфракрасная спектроскопия может использоваться для мониторинга хода реакции при условии, что реагент или продукт демонстрирует отчетливую оптическую плотность в ИК- области спектра. Скорость расхода реагентов и/или образования продукта можно абстрагировать от изменения оптической плотности с течением времени (путем применения закона Берса ). Даже когда спектры реагента и продукта в некоторой степени перекрываются, современное инструментальное программное обеспечение обычно способно точно выполнить деконволюцию относительных вкладов при условии, что с течением времени происходит резкое изменение абсолютного поглощения интересующего пика. ИК in situ можно классифицировать как интегральный метод, поскольку собранные первичные данные пропорциональны концентрации и времени. [2] На основе этих данных можно получить исходный материал или концентрацию продукта с течением времени, просто взяв интеграл полиномиальной аппроксимации экспериментальной кривой. [3] С увеличением доступности спектрометров с возможностью мониторинга на месте , в последние годы все шире используется FT-IR. Примеры, заслуживающие внимания, включают механистический анализ катализируемого амидо-тиомочевиной асимметричного синтеза Стрекера неприродных аминокислот, , а также основанием Льюиса , катализируемой галолактонизации и циклоэтерификации . [5] [6]
In situ УФ-Вид
[ редактировать ]Аналогично ИК-экспериментам in situ , описанным выше, in situ спектроскопия поглощения в УФ-видимой области может использоваться для мониторинга хода реакции при условии, что реагент или продукт демонстрирует различимое поглощение в УФ-области спектра . Скорость потребления реагентов и/или образования продукта можно абстрагировать от изменения оптической плотности с течением времени (путем применения закона Бера ), что снова приводит к классификации как интегральному методу. [2] Из-за используемого спектрального диапазона методы УФ-Вид чаще используются в неорганических или металлоорганических системах, чем в чисто органических реакциях, и примеры включают исследование самариевой реакции Барбье . [7]
Реакционная калориметрия
[ редактировать ]Калориметрию можно использовать для контроля за ходом реакции, поскольку контролируется мгновенный тепловой поток реакции, который напрямую связан с изменением энтальпии реакции. Реакционную калориметрию можно классифицировать как дифференциальный метод, поскольку собранные первичные данные пропорциональны скорости и времени. На основе этих данных можно получить исходный материал или концентрацию продукта с течением времени, просто взяв интеграл полиномиальной аппроксимации экспериментальной кривой. [2] [8] [9] Хотя реакционная калориметрия используется реже, чем ряд других методов, она нашла применение в качестве эффективного инструмента для скрининга катализаторов. [10] Реакционная калориметрия также применяется как эффективный метод изучения механизма отдельных реакций, включая пролинатом - катализируемое α аминирование альдегидов . [11] и палладием катализируемая реакция аминирования Бухвальда-Хартвига . [4] [12]
Дальнейшие методы
[ редактировать ]Хотя газовая хроматография , ВЭЖХ и масс-спектрометрия являются отличными методами различения смесей соединений (а иногда даже энантиомеров ), временное разрешение этих измерений менее точное, чем у методов, описанных выше. Тем не менее, эти методы все еще используются, например, при исследовании реакции Хека , где гетерогенная природа реакции не позволяет использовать методы, описанные выше. [13] и СОМО-активация органокатализаторами [14] Несмотря на свои недостатки, эти методы могут служить отличными методами калибровки.
Манипулирование и представление данных
[ редактировать ]
Данные о ходе реакции зачастую проще всего представить в виде графика зависимости концентрации субстрата ([A] t ) от времени ( t ) или конверсии фракции ( F ) от времени ( t ). Последнее требует незначительных алгебраических манипуляций для преобразования значений концентрации/поглощения в дробное преобразование ( F ) путем:
- Ф = [А] 0 - [А] т / [А] 0
где [A] 0 представляет собой количество, поглощение или концентрацию изначально присутствующего субстрата, а [A] t представляет собой количество, поглощение или концентрацию этого реагента в момент времени t . Нормализация данных до дробного преобразования может быть особенно полезной, поскольку позволяет сравнивать на одном графике несколько реакций, протекающих с разными абсолютными количествами или концентрациями.
Данные также обычно могут быть представлены в виде графика зависимости скорости реакции ( v ) от времени ( t ). Опять же, требуются простые алгебраические манипуляции; например, калориметрические эксперименты дают:
- v = q / V Δ H
где q — мгновенная теплопередача , Δ H — известное изменение энтальпии реакции, а V — реакционный объем . [2]
Данные экспериментов по кинетике хода реакции также часто представляются в виде графика зависимости скорости ( v ) от концентрации субстрата ([S]). Для этого необходимо получить и объединить как графики зависимости [S] от t, так и v графики зависимости от t, описанные выше (обратите внимание, что один может быть получен из другого путем простого дифференцирования или интегрирования). Комбинация приводит к стандартному набору кривых, на которых Ход реакции читается справа налево по оси X , а скорость реакции читается снизу вверх по Y. оси [2] Хотя эти графики часто обеспечивают визуально убедительную демонстрацию основных кинетических тенденций, дифференциальные методы обычно лучше подходят для извлечения числовых констант скорости. (см. ниже)
Каталитическая кинетика и состояние покоя катализатора
[ редактировать ]В каталитической кинетике два основных приближения полезны (в разных обстоятельствах) для описания поведения многих систем. Ситуации, в которых действительны приближения предварительного равновесия и стационарного состояния, часто можно отличить с помощью кинетического анализа хода реакции, и эти две ситуации тесно связаны с состоянием покоя катализатора.
Стационарное приближение
[ редактировать ]
В стационарных условиях катализатор и субстрат подвергаются обратимой ассоциации с последующим относительно быстрым расходованием комплекса катализатор-субстрат (как за счет прямых реакций с продуктом, так и обратных реакций с несвязанным катализатором). Приближение стационарного состояния предполагает, что концентрация комплекс катализатор-субстрат не меняется с течением времени; общая концентрация этого комплекса остается низкой, поскольку он уносится практически сразу после образования. Закон стационарной скорости содержит все константы скорости и виды, необходимые для перехода от исходного материала к продукту, а знаменатель состоит из суммы членов, описывающих относительные скорости прямой и обратной реакций, в которых потребляется устойчивое промежуточное соединение. Для простейшего случая, когда один субстрат переходит в один продукт через один промежуточный продукт:
- d [P] / dt = k 1 k 2 [A][Кошка] всего / k −1 + k 2
В немного более сложной ситуации, когда два субстрата последовательно связываются с последующим высвобождением продукта:
- d [P] / dt = k 1 k 2 k 3 [A][B][Cat] всего / k −1 k −2 + k −1 k 3 + k 2 k 3 [B]
Все более сложные системы можно описать просто с помощью алгоритма, описанного в этом справочнике. [15]
В случае описанных выше стационарных условий состояние покоя катализатора представляет собой несвязанную форму (поскольку связанное с субстратом промежуточное соединение по определению присутствует только в минимальной концентрации). [16]
Предравновесное приближение
[ редактировать ]
В предравновесных условиях катализатор и субстрат подвергаются быстрой и обратимой ассоциации перед относительно медленной стадией, ведущей к образованию и высвобождению продукта. В этих условиях система может быть описана законом скорости «один плюс», где числитель состоит из всех констант скорости и веществ, необходимых для перехода от исходного материала к продукту, а знаменатель состоит из суммы членов, описывающих каждый из состояния, в которых существует катализатор (и 1 соответствует свободному катализатору). [17] Для простейшего случая, когда один субстрат переходит в один продукт через один промежуточный продукт:
- d [P] / dt = К 1 к 2 [А][Кот] / 1 + К 1 [А]
В несколько более сложной ситуации, когда два субстрата последовательно связываются с последующим высвобождением продукта:
- d [P] / dt = К 1 К 2 к 3 [А][Б][Кот] / 1 + К 1 [А] + К 1 К 2 [А][Б]
В случае описанных выше простых предравновесных условий состоянием покоя катализатора является либо полностью, либо частично (в зависимости от величины константы равновесия) комплекс, связанный с субстратом.
Кинетика насыщения
[ редактировать ]Условия насыщения можно рассматривать как частный случай предравновесных условий. При исследуемой концентрации субстрата образование комплекса катализатор-субстрат происходит быстро и практически необратимо. Состояние покоя катализатора полностью состоит из связанного комплекса, и [A] больше не присутствует в законе скорости; изменение [A] не повлияет на скорость реакции, поскольку катализатор уже полностью связан и реагирует настолько быстро, насколько позволяет k 2 . Простейшим случаем кинетики насыщения является хорошо изученная Михаэлиса-Ментен модель кинетики ферментов .
Изменения в состоянии покоя катализатора
[ редактировать ]

Хотя реакция может демонстрировать один набор кинетических свойств на ранней стадии конверсии, это поведение может измениться из-за:
- изменения в состоянии покоя катализатора под влиянием изменения концентрации субстрата
- множественные или меняющиеся механизмы, на которые влияют концентрации субстрата или продукта
- активация катализатора (период инициации)
- ингибирование продукта
- необратимая (или обратимая) гибель катализатора
В случае кинетики насыщения, описанной выше, при условии, что [A] не присутствует в большом избытке по отношению к [B], условия насыщения будут применяться только в начале реакции. По мере расходования субстрата концентрация снижается, и в конечном итоге [А] становится недостаточно, чтобы полностью подавить [Кошку]. Это проявляется в постепенном изменении скорости от 0-го порядка к более высокому (т.е. 1-му, 2-му и т. д.) порядку по [А]. Это также можно описать как изменение состояния покоя катализатора из связанной формы в несвязанную форму в ходе реакции.
Помимо простого замедления реакции, изменение состояния покоя катализатора в ходе реакции может привести к конкурирующим путям или процессам. Для доступа к продукту может существовать несколько механизмов, и в этом случае порядок в катализаторе или субстрате может меняться в зависимости от условий или точки реакции. Особенно полезное исследование изменений в механизме реакции включает изучение нормализованной скорости реакции в зависимости от загрузки катализатора в нескольких фиксированных точках конверсии. Обратите внимание, что нормированная скорость реакции:
- к = v / [А] т
регулирует расход субстрата в ходе реакции, поэтому будут наблюдаться только изменения скорости из-за загрузки катализатора. Линейная зависимость от загрузки катализатора для данной конверсии указывает на зависимость первого порядка от катализатора при этой конверсии, и аналогичным образом можно представить себе нелинейные графики, возникающие в результате зависимости более высокого порядка. Изменения линейности или нелинейности от одного набора точек перехода к другому свидетельствуют об изменении зависимости от катализатора в ходе реакции. И наоборот, изменения в линейности или нелинейности областей графика, сохраняющиеся в нескольких точках конверсии (т.е. при 30, 50 и 70%), указывают на изменение зависимости от катализатора на основе абсолютной концентрации катализатора.
Взаимодействие катализатора с несколькими компонентами реакционной смеси может привести к сложной кинетической зависимости. Хотя взаимодействия катализатор-субстрат или катализатор-продукт вне цикла обычно считаются «ядовитыми» для системы (конечно, в случае необратимого комплексообразования), существуют случаи, когда частицы вне цикла фактически защищают катализатор от необратимой дезактивации. [19] [20] В любом случае часто бывает важно понять роль состояния покоя катализатора. [3] [11]
Эксперименты с одинаковым избытком
[ редактировать ]Переменным параметром, представляющим наибольший интерес при анализе кинетики протекания реакции, является избыток ( e ) одного субстрата над другим, выраженный в молярных единицах. Начальные концентрации двух веществ в реакции можно определить по формуле:
- [В] 0 = [А] 0 + е
и, предполагая стехиометрию реакции «один к одному», избыток одного субстрата над другим количественно сохраняется в течение всей реакции, так что: [3]
- [В] т = [А] т + е
Аналогичный набор можно построить для реакций со стехиометрией более высокого порядка, когда избыток предсказуемо меняется в ходе реакции. Хотя e может быть любым значением (положительным, отрицательным или нулевым), обычно в кинетическом анализе хода реакции используются положительные или отрицательные значения, меньшие по величине, чем один эквивалент субстрата. (Можно отметить, что в кинетике псевдонулевого порядка используются избыточные значения, гораздо большие по величине, чем один эквивалент субстрата).
Определение параметра избытка ( e ) позволяет построить эксперименты с одинаковым избытком, в которых два или более прогонов кинетического эксперимента с разными начальными концентрациями, но одинаковый избыток позволяют искусственно вступить в реакцию в любой точке. Эти эксперименты имеют решающее значение для RPKA каталитических реакций, поскольку они позволяют исследовать ряд механических возможностей, включая активацию катализатора (периоды индукции), дезактивацию катализатора и ингибирование продукта, описанное более подробно ниже. [2] [3]
Определение частоты оборота катализатора
[ редактировать ]Перед дальнейшим механистическим исследованием важно определить кинетическую зависимость интересующей реакции от катализатора. Частоту оборота (TOF) катализатора можно выразить как скорость реакции, нормированную на концентрацию катализатора:
- TOF = v / [Кот]
Этот TOF определяется путем проведения любых двух или более экспериментов с одинаковым избытком, в которых варьируется абсолютная концентрация катализатора. Поскольку концентрация катализатора постоянна в ходе реакции, полученные графики нормализуются на неизменяющуюся величину. Если полученные графики идеально совпадают, то реакция фактически является катализатором первого порядка. Если реакция не накладывается, значит, действуют процессы более высокого порядка, которые требуют более детального анализа, чем описано здесь. [3] Также стоит отметить, что описанная здесь манипуляция с наложением нормализации — это только один из подходов к интерпретации необработанных данных. Столь же достоверные результаты могут быть получены путем сопоставления наблюдаемого кинетического поведения смоделированным законам скорости.
Изучение активации и деактивации катализатора
[ редактировать ]
Как описано выше, эксперименты с одинаковым избытком проводятся с двумя или более экспериментами, поддерживающими постоянный избыток ( e ) при изменении абсолютных концентраций субстратов (в этом случае катализатор также рассматривается как субстрат). Обратите внимание, что эта конструкция приводит к тому, что количество эквивалентов и, следовательно, мольный процент каждого реагента/катализатора различаются в разных реакциях. [3] Эти эксперименты позволяют искусственно «войти» в реакцию в любой момент, поскольку начальные концентрации одного эксперимента (перехватывающая реакция) выбираются так, чтобы напрямую сопоставляться с ожидаемыми концентрациями в некоторый промежуточный момент времени t в другом (родительская реакция). . Можно было бы ожидать, что ход реакции, описанный графиками зависимости скорости от концентрации субстрата, подробно описанными выше, будет напрямую накладываться друг на друга, начиная с этой точки перехвата. Однако это будет справедливо только в том случае, если скорость реакции не изменится из-за изменений концентрации активного субстрата/катализатора (например, за счет активации катализатора, дезактивации катализатора или ингибирования продукта) до этого перехвата. [2] [3]
Идеальное наложение нескольких экспериментов с одинаковыми избыточными, но разными начальными загрузками субстрата позволяет предположить, что в ходе реакции не происходит никаких изменений в концентрации активного субстрата/катализатора. Отсутствие наложения графиков обычно указывает на активацию, дезактивацию или ингибирование продукта в условиях реакции. Эти случаи можно отличить по положению кривых хода реакции относительно друг друга. Перехват реакций, лежащих ниже (более медленные скорости при той же концентрации субстрата) исходных реакций на графике зависимости скорости от концентрации субстрата, указывает на активацию катализатора в условиях реакции. Перехват реакций, лежащих выше (более высокие скорости при той же концентрации субстрата) исходных реакций на графике зависимости скорости от концентрации субстрата, указывает на дезактивацию катализатора в условиях реакции; необходимы дальнейшие эксперименты, чтобы отличить ингибирование продукта от других форм гибели катализатора. [2]
Одним из ключевых различий между реакцией перехвата и исходной реакцией, описанной выше, является присутствие некоторого количества продукта исходной реакции в точке перехвата. Давно известно, что ингибирование продукта влияет на эффективность катализатора многих систем, а в случае экспериментов с одинаковым избытком оно предотвращает наложение перехватывающей и исходной реакций. Хотя описанные выше эксперименты с одинаковым избытком не могут объяснить дезактивацию катализатора какой-либо конкретной причиной, ингибирование продукта можно проверить с помощью дальнейших экспериментов, в которых некоторое начальное количество продукта добавляется к перехватывающей реакции (с целью имитировать количество ожидаемого присутствия продукта). в исходной реакции при той же концентрации субстрата). Идеальное наложение графиков зависимости скорости от концентрации субстрата в условиях «тот же избыток-тот же продукт» указывает на то, что ингибирование продукта действительно происходит в используемых условиях реакции. Хотя отсутствие наложения графиков зависимости скорости от концентрации субстрата в условиях «тот же избыток-тот же продукт» не исключает ингибирования продукта, это, по крайней мере, указывает на то, что другие пути дезактивации катализатора также должны быть активными.
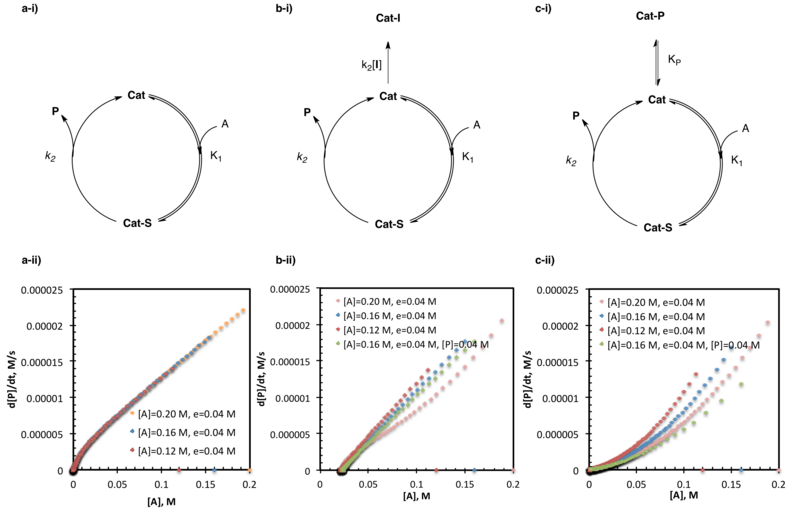
Эксперименты с одинаковым избытком, исследующие дезактивацию катализатора и ингибирование продуктов, являются одними из наиболее широко используемых применений кинетического анализа хода реакции. Среди многочисленных примеров в литературе некоторые включают исследование алкилирования цинком альдегидов, катализируемого аминоспиртами. [21] амидо -тиомочевина, катализируемая асимметричным синтезом Стрекера неприродных аминокислот , [5] и СОМО-активация органокализаторов. [14]
Определение стехиометрии реакции
[ редактировать ]Дифференциальные методы извлечения констант скорости
[ редактировать ]Благодаря большому количеству данных, доступных в результате мониторинга хода реакции с течением времени, в сочетании с мощью современных вычислительных методов, стало достаточно просто численно оценить закон скорости, сопоставляя интегрированные законы скорости смоделированных путей реакций с соответствием хода реакции с течением времени. . Благодаря принципам распространения ошибок константы скорости и законы скорости могут быть определены этими дифференциальными методами со значительно меньшей неопределенностью, чем при построении графических уравнений скорости (выше). [9]
Разно-избыточные эксперименты
[ редактировать ]Хотя РПКА позволяет наблюдать скорости на протяжении всей реакции, проведение экспериментов только с одинаковым избытком не дает достаточной информации для определения соответствующих констант скорости. Чтобы построить достаточно независимых отношений для решения всех неизвестных констант скорости, необходимо изучить системы с различным избытком.
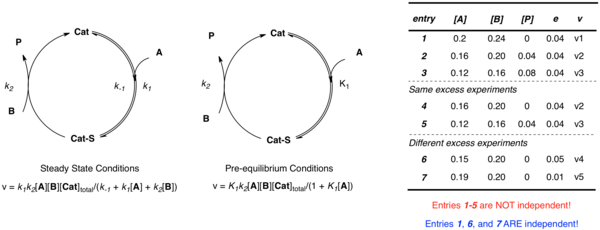
Рассмотрим еще раз простой пример, рассмотренный выше, где катализатор связывается с субстратом A, после чего следует реакция с B с образованием продукта P и свободного катализатора. Независимо от применяемого приближения, для определения системы требуется несколько независимых параметров ( k 2 и K 1 в случае предварительного равновесия; k 1 , k -1 и k 2 в случае установившегося состояния). Хотя можно представить себе построение нескольких уравнений для описания неизвестных при разных концентрациях, когда данные получены в результате эксперимента с одинаковым избытком, [A] и [B] не являются независимыми:
- е = [В] − [А]
несколько экспериментов с использованием разных значений e, Необходимо чтобы установить несколько независимых уравнений, определяющих несколько независимых констант скорости с точки зрения экспериментальных скоростей и концентраций. Затем можно использовать нелинейный анализ наименьших квадратов для получения значений, наилучшим образом соответствующих неизвестным константам скорости этим уравнениям.
Графические законы скорости
[ редактировать ]
Кинетики исторически полагались на линеаризацию данных о скорости для экстраполяции констант скорости, что, возможно, лучше всего демонстрирует широкое использование стандартной Лайнуивера-Берка линеаризации уравнения Михаэлиса-Ментен . [22] Методы линеаризации имели особое значение до появления вычислительных методов, способных аппроксимировать сложные кривые, и они остаются основным продуктом кинетики из-за их интуитивно простого представления. [2] Важно отметить, что методы линеаризации НЕ следует использовать для извлечения числовых констант скорости, поскольку они вносят большую степень ошибки по сравнению с альтернативными численными методами. Однако графические законы скорости поддерживают интуитивное представление линеаризованных данных, так что визуальный осмотр графика может дать механистическое представление о рассматриваемой реакции. В основе графического закона скорости лежат графики зависимости скорости ( v ) от концентрации субстрата ([S]), обсуждавшиеся выше. Например, в простом цикле, обсуждаемом применительно к экспериментам с различным избытком, график v / [A] против [B] и его близнеца v / [B] в зависимости от [A] может дать интуитивное представление о порядке каждого из реагентов. Если участки Наложение v / [A] vs. [B] для нескольких экспериментов с различным избытком, данные согласуются с зависимостью первого порядка от [A]. То же самое можно сказать и о сюжете v / [B] vs. [A]; наложение соответствует зависимости первого порядка от [B]. Возможны неперекрывающиеся результаты этих графических законов скорости, которые указывают на зависимость более высокого порядка от исследуемых подложек. Блэкмонд предложила представить результаты экспериментов с различным избытком с помощью ряда графических уравнений скорости (которые она представляет в адаптированной здесь блок-схеме), но важно отметить, что предложенный ею метод является лишь одним из многих возможных методов отображения кинетическая связь. Кроме того, хотя представление законов скорости в графическом виде иногда можно считать визуально упрощенным способом представления сложных кинетических данных, для извлечения точных и количественных констант скорости и порядков реакций необходима подгонка необработанных кинетических данных для анализа с помощью дифференциальных или других строгих численных методов. . [2] [3]
Стехиометрия и механизм реакции
[ редактировать ]Важно отметить, что хотя кинетический анализ является мощным инструментом для определения стехиометрии переходного состояния, ограничивающего оборот, относительно основного состояния, он не может ответить на все вопросы механизма. Два механизма могут быть кинетически неразличимы, особенно в каталитических условиях. Для любой тщательной механистической оценки необходимо провести кинетический анализ как каталитического процесса, так и его отдельных стадий (когда это возможно) в сочетании с другими формами анализа, такими как оценка линейных соотношений свободной энергии , изотопного эффекта исследования , компьютерный анализ или любой другой анализ. количество альтернативных подходов. Наконец, важно отметить, что ни одна механистическая гипотеза никогда не может быть доказана; альтернативную механистическую гипотезу можно только опровергнуть. Поэтому крайне важно проводить любое исследование на основе гипотез. Только экспериментально опровергнув разумные альтернативы, можно усилить поддержку данной гипотезы. [23]
См. также
[ редактировать ]- Химическая кинетика
- Кинетика ферментов
- Уравнение Хилла (биохимия)
- Модель адсорбции Ленгмюра
- Кинетика Михаэлиса-Ментен
- Уравнение Моно
- Уравнение скорости (химия)
- Механизм реакции
- Устойчивое состояние (химия)
Ссылки
[ редактировать ]- ^ Jump up to: а б Хартвиг, Дж. Ф. (2010). Химия органопереходных металлов: от связывания к катализу . Милл-Вэлли, Калифорния: Университетские научные книги. ISBN 978-1-891389-53-5 .
- ^ Jump up to: а б с д и ж г час я дж к л м Блэкмонд, генеральный директор (2005). «Кинетический анализ хода реакции: мощная методология механистических исследований сложных каталитических реакций». Энджью. хим. Межд. Эд. 44 (28): 4302–4320. дои : 10.1002/anie.200462544 . ПМИД 15997457 .
- ^ Jump up to: а б с д и ж г час я Блэкмонд, генеральный директор; Ропич, М.; Стефинович, М. (2006). «Кинетические исследования асимметричного переноса гидрирования иминов муравьиной кислотой, катализируемого Rh-диаминовыми катализаторами». Орг. Процесс Рез. Дев. 10 (3): 457–463. дои : 10.1021/op060033k .
- ^ Jump up to: а б Шекхар, С.; Райберг, П.; Хартвиг, Дж. Ф.; Мэтью, Дж.С.; Блэкмонд, генеральный директор; Стритер, скорая помощь; Бухвальд, СЛ (2006). «Переоценка механизма аминирования арилгалогенидов, катализируемого BINAP-лигированными палладиевыми комплексами». Дж. Ам. хим. Соц. 128 (11): 3584–3591. дои : 10.1021/ja045533c . ПМИД 16536531 .
- ^ Jump up to: а б Зюэнд, SJ ; Якобсен, Э.Н. (2009). «Механизм энантиоселективного гидроцианирования имина, катализируемого амидо-тиомочевиной: стабилизация переходного состояния посредством множественных нековалентных взаимодействий» . Дж. Ам. хим. Соц. 131 (42): 15358–15374. дои : 10.1021/ja9058958 . ПМЦ 2783581 . ПМИД 19778044 .
- ^ Дания, Южная Дания ; Берк, Монтана (2010). «Катализ основаниями Льюиса бром- и иодолактонизации и циклоэтерификации» . Учеб. Натл. акад. наук. 107 (48): 20655–20660. Бибкод : 2010PNAS..10720655D . дои : 10.1073/pnas.1005296107 . ПМЦ 2996424 . ПМИД 20705900 .
- ^ Шокетт, Калифорния; Садашивам, Д.В.; Цветы, РА (2011). «Каталитический Ni(II) в реакциях SmI 2 : химия на основе Sm(II) или Ni(0)?». Дж. Ам. хим. Соц. 133 (27): 10655–10661. дои : 10.1021/ja204287n . ПМИД 21619012 .
- ^ Мэтью, Дж.С.; Клуссманн, М.; Ивамура, Х.; Валера, Ф.; Футран, А; Эмануэльссон, EAC; Блэкмонд, Д.Г. (1999). «Исследование реакций сочетания ArX, катализируемых Pd, на основе кинетического анализа хода реакции». Дж. Орг. хим. 71 (13): 4711–4722. дои : 10.1021/jo052409i . ПМИД 16776495 .
- ^ Jump up to: а б Сталь, К.; Накуви, КР (1991). «Дифференциальный метод в химической кинетике». Дж. Физ. хим. 95 (26): 10703–10718. дои : 10.1021/j100179a037 .
- ^ Блэкмонд, Д.Г. ; Рознер, Т.; Пфальц, А. (1999). «Комплексный кинетический скрининг катализаторов с использованием реакционной калориметрии». Орг. Процесс Рез. Дев. 3 (4): 275–280. дои : 10.1021/op990024u .
- ^ Jump up to: а б Хейн, Дж. Э.; Армстронг, А.; Блэкмонд, генеральный директор (2011). «Кинетическое профилирование катализируемого пролинатом α-аминирования альдегидов». Орг. Летт. 13 (16): 4300–4303. дои : 10.1021/ol201639z . ПМИД 21761822 .
- ^ Сингх, Великобритания; Стритер, скорая помощь; Блэкмонд, генеральный директор; Бухвальд, СЛ (2002). «Механистический взгляд на катализируемое Pd (BINAP) аминирование арилбромидов: кинетические исследования в синтетически значимых условиях». Дж. Ам. хим. Соц. 124 (47): 14104–14114. дои : 10.1021/ja026885r . ПМИД 12440909 .
- ^ Херрманн, Вашингтон; Броссмер, К.; Райзингер, CP; Рирмайер, TH; Офеле, К.; Беллер, М. (1997). «Палладациклы: новые эффективные катализаторы для чертовски винилирования арилгалогенидов». хим. Евро. Дж. 3 (8): 1357–1364. дои : 10.1002/chem.19970030823 .
- ^ Jump up to: а б Девери, Джей-Джей; Конрад, JC; Макмиллан, DWC; Цветы, РА (2010). «Механистическая сложность органо-СОМО-активации» . Энджью. хим. Межд. Эд. 49 (35): 6106–6110. дои : 10.1002/anie.201001673 . ПМК 3065936 . ПМИД 20632343 .
- ^ Гилберт, Х.Ф. (1977). « Практическое правило» для вывода уравнений скорости установившегося состояния». Дж. Хим. Образование. 54 (8): 492–493. Бибкод : 1977ЖЧЭд..54..492Г . дои : 10.1021/ed054p492 .
- ^ «4.12: Стационарное приближение» . 22 июля 2015 г.
- ^ Хельферих, ФГ (1989). «Систематический подход к объяснению многоступенчатых реакционных сетей». Дж. Физ. хим. 93 (18): 6676–6681. дои : 10.1021/j100355a022 .
- ^ Зюэнд, С.Дж.; Якобсен, Э.Н. (2007). «Механистическая схема и кинетические данные адаптированы на основе независимого кинетического моделирования с использованием констант скорости и равновесия, указанных для цианозилирования кетонов, катализируемого аминотиомочевиной». Дж. Ам. хим. Соц . 129 (51): 15872–15883. дои : 10.1021/ja0735352 . ПМИД 18052247 .
- ^ Лист, Б. (2002). «Асимметричные реакции, катализируемые пролином». Тетраэдр . 58 (28): 5573–5590. дои : 10.1016/S0040-4020(02)00516-1 .
- ^ Зеебах, Д.; Бек, АК; Бадин, DM; Лимбах, М.; Эшенмозер, А.; Казначейство, AM; Хоби, Р.; Прикошович, В. (2007). «Действительно ли оксазолидиноны непродуктивны и являются паразитическими видами в пролиновом катализе? - Мысли и эксперименты, указывающие на альтернативную точку зрения» . Хелв. Хим. Акта . 90 (3): 425–471. дои : 10.1002/hlca.200790050 .
- ^ Рознер, Т.; Сирс, Пи Джей; Ньюджент, Вашингтон; Блэкмонд. ГД (2000). «Кинетические исследования ингибирования продуктов асимметричного алкилирования бензальдегида диэтилцинком, катализируемого аминоспиртами». Орг. Летт. 2 (16): 2511–2513. дои : 10.1021/ol006181r . ПМИД 10956534 .
- ^ Лайнуивер, Х .; Берк, Д. (1934). «Определение констант диссоциации ферментов». Дж. Ам. хим. Соц. 56 (3): 658–666. дои : 10.1021/ja01318a036 .
- ^ Платт, младший (1964). «Сильный вывод». Наука . 146 (3642): 347–353. Бибкод : 1964Sci...146..347P . дои : 10.1126/science.146.3642.347 . ПМИД 17739513 .