Кельвин
| Кельвин | |
|---|---|
 Эквивалентные температуры в Кельвинах (K), Цельсиях (°C) и Фаренгейтах (°F). | |
| Общая информация | |
| Система единиц | И |
| Единица | температура |
| Символ | К |
| Назван в честь | Уильям Томсон, первый барон Кельвин |
| определение 2019 года | к Б ≝ 1,380 649 × 10 −23 J / K |
| Конверсии | |
| х К в... | ... соответствует... |
| Цельсия | ( х − 273,15) °С |
| Фаренгейт | (1,8 х - 459,67) ° F |
| Рэнкин | 1,8 х °Ra |
Кельвин , , символ К является базовой единицей измерения температуры в Международной системе единиц (СИ). Шкала Кельвина — это абсолютная шкала температур , которая начинается с 0 К, самой низкой возможной температуры ( абсолютный ноль ), а затем повышается ровно на 1 К на каждый 1 °С. [1] [2] [3] [4] Шкала Кельвина была разработана таким образом, чтобы ее можно было легко преобразовать из шкалы Цельсия (обозначение °C). Любую температуру в градусах Цельсия можно перевести в Кельвины, добавив 273,15. [1] [5]
Британский ученый XIX века лорд Кельвин первым разработал и предложил шкалу. [5] В начале 20 века ее часто называли «абсолютной шкалой Цельсия». [6] Кельвин был официально добавлен в Международную систему единиц в 1954 году, определив 273,16 К как тройную точку воды . Используя это определение, шкалы Цельсия, Фаренгейта и Рэнкина были переопределены в терминах шкалы Кельвина. [2] [7] [8] Переопределение базовых единиц СИ в 2019 году теперь определяет кельвин с точки зрения энергии, устанавливая постоянную Больцмана 1,380 точно равной 649 × 10 . −23 джоули на кельвин; [2] каждое изменение термодинамической температуры на 1 К соответствует изменению тепловой энергии ровно на 1,380 649 × 10. −23 Дж .
История
[ редактировать ]Прекурсоры
[ редактировать ]
В XVIII веке несколько температурных шкал . было разработано [9] особенно градусы Фаренгейта и Цельсия (позже Цельсия). Эти шкалы предшествовали большей части современной науки термодинамики , включая атомную теорию и кинетическую теорию газов , которые лежат в основе концепции абсолютного нуля. Вместо этого они выбрали определяющие точки в пределах человеческого опыта, которые можно было легко и с достаточной точностью воспроизвести, но которые не имели какого-либо глубокого значения для теплофизики. В случае шкалы Цельсия (а также давно несуществующей шкалы Ньютона и шкалы Реомюра ) такой отправной точкой служила точка плавления льда, причем цель Цельсия определялась (с 1740-х по 1940-е годы ) путем калибровки термометра таким образом, чтобы:
- воды Температура замерзания составляет 0°С.
- воды Температура кипения составляет 100°С.
Это определение предполагает наличие чистой воды при определенном давлении , приближенном к естественному давлению воздуха на уровне моря. Таким образом, приращение на 1 °С равно 1/100 кипения . разницы температур между точками плавления и Тот же температурный интервал позже был использован для шкалы Кельвина.
Закон Чарльза
[ редактировать ]С 1787 по 1802 год его определяли Жак Шарль (неопубликовано), Джон Дальтон , [10] [11] и Жозеф Луи Гей-Люссак [12] что при постоянном давлении идеальные газы линейно расширяют или сжимают свой объем ( закон Чарльза ) примерно на 1/273 части на градус Цельсия при изменении температуры вверх или вниз, в диапазоне от 0 ° C до 100 ° C. Экстраполяция этого закона показала, что газ, охлажденный примерно до -273 ° C, будет занимать нулевой объем.
Лорд Кельвин
[ редактировать ]
Первая абсолютная шкала
[ редактировать ]В 1848 году Уильям Томсон, который позже был удостоен титула лорда Кельвина , опубликовал статью «Об абсолютной термометрической шкале» . [13] Предложенная в статье шкала оказалась неудовлетворительной, но принципы и формулы, на которых основывалась шкала, оказались правильными. [14] Например, в сноске Томсон вывел значение -273 ° C для абсолютного нуля, рассчитав отрицательную обратную величину 0,00366 — коэффициент теплового расширения идеального газа на градус Цельсия относительно точки льда. [15] Это полученное значение согласуется с принятым в настоящее время значением -273,15 °C, что позволяет учитывать точность и неопределенность расчетов.
Шкала была разработана по принципу, что «единица теплоты, нисходящая от тела А с температурой Т ° этой шкалы к телу В с температурой ( Т - 1)° , будет давать один и тот же механический эффект, каким бы ни было быть числом Т ». [16] В частности, Томсон выразил объем работы, необходимой для производства единицы тепла ( тепловой КПД ), как , где температура в градусах Цельсия, - коэффициент теплового расширения, а была «функция Карно», независимая от вещества величина, зависящая от температуры, [17] мотивировано устаревшей версией теоремы Карно . [14] [18] Шкала получается путем нахождения замены переменных температуры такой, что пропорционально .
Когда Томсон опубликовал свою статью в 1848 году, он рассматривал только экспериментальные измерения Реньо. . [19] В том же году Джеймс Прескотт Джоуль предположил Томсону, что истинная формула функции Карно выглядит так: [20] где это «механический эквивалент единицы тепла», [21] теперь называемая удельной теплоемкостью воды, она составляет примерно 771,8 фут-фунт-сила на градус Фаренгейта на фунт (4153 Дж/К/кг). [22] Томсон изначально скептически относился к отклонениям формулы Джоуля от эксперимента, заявляя: «Я думаю, будет общепризнано, что в части данных Рено не может быть такой неточности, и остается только неопределенность относительно плотности насыщенного пара». [23] Томсон назвал правильность формулы Джоуля « гипотезой Майера », поскольку она была впервые выдвинута Майером. [24] Томсон организовал многочисленные эксперименты совместно с Джоулем и в конце концов к 1854 году пришел к выводу, что формула Джоуля верна и что влияние температуры на плотность насыщенного пара объясняет все расхождения с данными Реньо. [25] Поэтому по современной шкале Кельвина , первая шкала может быть выражена следующим образом: [18] Параметры шкалы были выбраны произвольно так, чтобы они совпадали со шкалой Цельсия при 0 и 100 °С или 273 и 373 К (температуры плавления и кипения воды). [26] В этой шкале увеличение примерно на 222 градуса соответствует удвоению температуры Кельвина независимо от начальной температуры, а «бесконечный холод» ( абсолютный ноль ) имеет числовое значение отрицательной бесконечности . [27]
Современная абсолютная шкала
[ редактировать ]Томсон понял, что с помощью предложенной Джоулем формулы для , соотношение между работой и теплом для идеального термодинамического двигателя было просто константой . [28] Таким образом, в 1854 году Томсон и Джоуль сформулировали вторую абсолютную шкалу, которая была более практичной и удобной и для большинства целей согласовывалась с воздушными термометрами. [29] В частности, «числовая мера температуры должна быть просто механическим эквивалентом тепловой единицы, разделенной на функцию Карно». [30]
Чтобы объяснить это определение, рассмотрим обратимый двигатель с циклом Карно , где - количество тепловой энергии, переданной в систему, это тепло, покидающее систему, это работа, совершенная системой ( ), - температура горячего резервуара в градусах Цельсия, а – температура холодного резервуара в градусах Цельсия. Функция Карно определяется как , а абсолютная температура как . Человек обнаруживает отношения . Полагая , получается общий принцип абсолютной термодинамической температурной шкалы для двигателя Карно: . Можно показать, что это определение соответствует термометрической температуре законов идеального газа . [31]
Это определение само по себе недостаточно. Томсон указал, что шкала должна иметь два свойства: [32]
- Абсолютные значения двух температур относятся друг к другу как отношение теплоты, забираемой к теплу, отдаваемому в идеальной термодинамической машине, работающей с источником и холодильником при более высокой и более низкой из температур соответственно.
- Разность температур замерзания и кипения воды при нормальном атмосферном давлении называется 100 градусами. (То же самое, что и по шкале Цельсия). Лучшие оценки Томсона в то время заключались в том, что температура замерзающей воды составляла 273,7 К, а температура кипящей воды - 373,7 К. [33]
Эти два свойства будут присутствовать во всех будущих версиях шкалы Кельвина, хотя под этим названием она еще не была известна. В первые десятилетия 20-го века шкалу Кельвина часто называли шкалой «абсолютного Цельсия », указывая градусы Цельсия, отсчитываемые от абсолютного нуля, а не от точки замерзания воды, и используя тот же символ для обычных градусов Цельсия, °C. [6]
Трехточечный стандарт
[ редактировать ]
В 1873 году старший брат Уильяма Томсона Джеймс ввёл термин «тройная точка». [34] для описания сочетания температуры и давления , при котором твердая, жидкая и газовая фазы вещества способны сосуществовать в термодинамическом равновесии . В то время как любые две фазы могут сосуществовать в диапазоне комбинаций температуры и давления (например, на температуру кипения воды можно существенно повлиять повышением или понижением давления), условие тройной точки для данного вещества может возникнуть только при одном давлении и только при одной температуре. К 1940-м годам экспериментально измеренная тройная точка воды составляла около 0,6% стандартного атмосферного давления и очень близко к 0,01 ° C согласно историческому определению Цельсия, которое тогда использовалось.
В 1948 году шкала Цельсия была перекалибрована путем присвоения тройной температуре воды значения ровно 0,01 °C. [35] и обеспечение того, чтобы температура плавления при стандартном атмосферном давлении имела эмпирически определенное значение (а фактическая точка плавления при атмосферном давлении имела колеблющееся значение), близкое к 0 °C. Это было оправдано тем, что тройная точка считалась более точно воспроизводимой эталонной температурой, чем точка плавления. [36] Тройную точку можно измерить с точностью ±0,0001 °C, а температуру плавления — с точностью ±0,001 °C. [35]
В 1954 году, когда экспериментально было установлено, что абсолютный ноль составляет около -273,15 °C согласно используемому тогда определению °C, Резолюция 3 10-й Генеральной конференции по мерам и весам (CGPM) ввела новую международно стандартизированную шкалу Кельвина, которая определяла тройная точка равна ровно 273,15 + 0,01 = 273,16 градуса Кельвина. [37] [38]
В 1967/1968 году Резолюция 3 13-й ГКМВ переименовала единицу приращения термодинамической температуры в «кельвин», символ К, заменив «градус Кельвина», символ °К. [39] [40] [41] 13-я ГКМВ также постановила в Резолюции 4, что «Кельвин, единица термодинамической температуры, равен дроби 1 / 273,16 термодинамической температуры тройной точки воды». [4] [42] [43]
После переопределения метра в 1983 году кельвин, секунда и килограмм остались единственными единицами СИ, не определяемыми по отношению к какой-либо другой единице.
В 2005 году, отметив, что на тройную точку может влиять изотопное соотношение водорода и кислорода, составляющих пробу воды, и что это «теперь является одним из основных источников наблюдаемой изменчивости между различными реализациями тройной точки воды», Международный комитет мер и весов (CIPM), комитет CGPM, подтвердил, что для целей определения температуры тройной точки воды определение кельвина будет относиться к воде, имеющей изотопный состав, указанный Венским стандартом. Средняя океанская вода . [4] [44] [45]
переопределение 2019 года
[ редактировать ]
В 2005 году CIPM начал программу по переопределению кельвина (наряду с другими базовыми единицами СИ ) с использованием более строгого экспериментального метода. В частности, комитет предложил переопределить кельвин так, чтобы постоянная Больцмана ( k B ) принимала точное значение 1,380 6505 × 10. −23 Дж/К . [46] Комитет надеялся, что программа будет завершена к моменту ее принятия ГКМВ на ее заседании в 2011 году, но на заседании 2011 года решение было отложено до заседания 2014 года, когда она будет считаться частью более широкой программы . [47] Задача заключалась в том, чтобы избежать снижения точности измерений вблизи тройной точки. Переопределение было отложено в 2014 году в ожидании более точных измерений постоянной Больцмана с точки зрения текущего определения. [48] но был окончательно принят на 26-й ГКМВ в конце 2018 года со значением k B = 1,380 649 × 10. −23 J⋅K −1 . [49] [46] [1] [2] [4] [50]
Для научных целей главное преимущество нового определения заключается в том, что оно позволяет проводить более точные измерения при очень низких и очень высоких температурах, поскольку используемые методы зависят от постоянной Больцмана. Независимость от какого-либо конкретного вещества или измерения также является философским преимуществом. Кельвин теперь зависит только от постоянной Больцмана и универсальных констант (см. Диаграмму зависимостей единиц СИ 2019 года), что позволяет выражать кельвин точно так: [2]
- 1 Кельвин = 1.380 649 × 10 −23 / ( 6.626 070 15 × 10 −34 )( 9 192 631 770 ) h Δ ν Cs / k B = 13.806 49 / 6.091 102 297 113 866 55 h Δ ν Cs / k B .
Для практических целей переопределение осталось незамеченным; Для константы Больцмана было использовано достаточно цифр, чтобы гарантировать, что 273,16 К имеет достаточно значащих цифр , чтобы сдержать неопределенность тройной точки воды. [51] и вода все еще обычно замерзает при температуре 0 °C. [52] с высокой степенью точности. Но до переопределения тройная точка воды была точной, а постоянная Больцмана имела измеренное значение 1,380 649 03 (51) × 10. −23 Дж/К с относительной стандартной неопределенностью 3,7 × 10. −7 . [51] После этого константа Больцмана становится точной, и неопределенность переносится на тройную точку воды, которая теперь равна 273,1600(1) К. [а]
Новое определение официально вступило в силу 20 мая 2019 года, в 144-ю годовщину Метрической конвенции . [50] [1] [2] [4]
Практическое использование
[ редактировать ]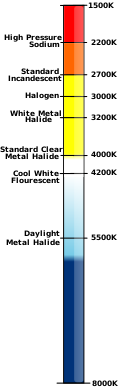
Цветовая температура
[ редактировать ]Кельвин часто используется как мера цветовой температуры источников света. Цветовая температура основана на принципе, согласно которому излучатель черного тела излучает свет с частотным распределением, характерным для его температуры. Черные тела при температуре ниже 4000 К кажутся красноватыми, тогда как при температуре выше 7500 К кажутся голубоватыми. Цветовая температура важна в области проекции изображений и фотографии, где цветовая температура около 5600 К. для соответствия пленочным эмульсиям «дневного света» требуется
В астрономии звездная классификация звезд и их место на диаграмме Герцшпрунга-Рассела частично основана на температуре их поверхности, известной как эффективная температура . Фотосфера Солнца , например, имеет эффективную температуру 5772 К [1] [2] [3] [4] , как это принято Резолюцией B3 МАС 2015 года.
Цифровые камеры и программное обеспечение для фотосъемки часто используют цветовую температуру в K в меню редактирования и настройки. Простое объяснение заключается в том, что более высокая цветовая температура создает изображение с улучшенными оттенками белого и синего. Снижение цветовой температуры приводит к тому, что в изображении преобладают красноватые, «более теплые» цвета .
Кельвин как единица шумовой температуры
[ редактировать ]В электронике кельвин используется как индикатор того, насколько шумна схема по отношению к предельному уровню шума , то есть шумовой температуре . Шум Джонсона-Найквиста резисторов постоянной (который создает соответствующий kTC шум в сочетании с конденсаторами ) представляет собой тип теплового шума, полученный из Больцмана , и может использоваться для определения шумовой температуры цепи с использованием формул Фрииса для шума .
Производные единицы и кратные СИ
[ редактировать ]Единственная производная единица системы СИ, имеющая особое название, происходящее от кельвина, — это градус Цельсия. Как и другие единицы СИ, кельвин также можно изменить, добавив метрический префикс , который умножает его на 10 :
| Дробные | Множители | ||||
|---|---|---|---|---|---|
| Ценить | символ СИ | Имя | Ценить | символ СИ | Имя |
| 10 −1 К | дК | децикельвин | 10 1 К | даК | декакельвин |
| 10 −2 К | СК | в сантикельвинах | 10 2 К | Гонконг | гектокельвин |
| 10 −3 К | мК | милликельвин | 10 3 К | кК | килокельвин |
| 10 −6 К | мкК | микрокельвин | 10 6 К | МК | мегакельвин |
| 10 −9 К | и т. д. | нанокельвин | 10 9 К | ГК | гигакельвин |
| 10 −12 К | ПК | пикокельвин | 10 12 К | ТК | теракельвин |
| 10 −15 К | ФК | фемтокельвин | 10 15 К | ПК | петакельвин |
| 10 −18 К | АК | Аттокельвин | 10 18 К | я | эксакельвин |
| 10 −21 К | зК | цептокельвин | 10 21 К | ЗК | зеттакельвин |
| 10 −24 К | yK | йоктокельвин | 10 24 К | ЮК | йоттакельвин |
| 10 −27 К | РК | Фаллелвин | 10 27 К | РК | Роннакельвин |
| 10 −30 К | qK | квиктокельвин | 10 30 К | КК | кветкельвин |
Орфография
[ редактировать ]Согласно соглашению СИ, кельвин никогда не упоминается и не пишется как градус . Слово «кельвин» не пишется с заглавной буквы, когда используется в качестве единицы измерения. При необходимости оно может быть в форме множественного числа (например, «на улице 283 градуса по Цельсию», а «на улице 50 градусов по Фаренгейту» и «10 градусов по Цельсию»). [54] [5] [55] [56] Обозначение устройства K — заглавная буква. [39] согласно соглашению СИ, символы единиц, производные от имени человека, следует писать с заглавной буквы. [57] При обращении к лорду Кельвину принято писать с заглавной буквы. [5] или шкале Кельвина. [58]
Символ единицы K кодируется в Юникоде в кодовой точке U+212A К ЗНАК КЕЛЬВИНА . Однако это символ совместимости , предусмотренный для совместимости с устаревшими кодировками. Стандарт Unicode рекомендует использовать U + 004B K ЛАТИНСКАЯ ЗАГЛАВНАЯ БУКВА K Вместо есть нормальный капитал К. ; то «Три буквоподобных символа получили каноническую эквивалентность обычным буквам: U+2126 Ом ЗНАК ОМА , U+212A K ЗНАК КЕЛЬВИНА и U+212B ЗНАК АНГСТРОМА . Во всех трех случаях следует использовать обычную букву». [59]
См. также
[ редактировать ]- Сравнение температурных шкал
- Международная температурная шкала 1990 г.
- кТ (энергия) – произведение постоянной Больцмана и температуры.
- Отрицательная температура
- Очерк метрологии и измерений
Примечания
[ редактировать ]Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д МБМВ (20 мая 2019 г.). «Практическая практика для определения кельвина в системе СИ» . BIPM.org . Проверено 18 февраля 2022 г.
- ^ Перейти обратно: а б с д и ж «Брошюра СИ: Международная система единиц (СИ) – 9-е издание (обновлено в 2022 г.)» . БИПМ . Проверено 7 сентября 2022 г.
- ^ «Базовая единица СИ: кельвин (К)» . БИПМ . Проверено 5 марта 2022 г.
- ^ Перейти обратно: а б с д и «Поворотный момент для человечества: новое определение мировой системы измерений» . НИСТ . 12 мая 2018 г. Проверено 21 февраля 2022 г.
- ^ Перейти обратно: а б с д «Кельвин: Введение» . НИСТ . 14 мая 2018 г. Проверено 2 сентября 2022 г.
- ^ Перейти обратно: а б Издания Британской энциклопедии 1920-х и 1950-х годов, статья «Планеты».
- ^ Бенхэм, Элизабет (06 октября 2020 г.). «Разрушение мифов о метрической системе» . НИСТ . Take Measure (официальный блог NIST) . Проверено 21 февраля 2022 г.
- ^ «Справочник 44 – 2022 – Приложение C – Общие таблицы единиц измерения» (PDF) . nist.gov . НИСТ . Проверено 21 февраля 2022 г.
- ^ «Кельвин: История» . НИСТ . 14 мая 2018 г. Проверено 21 февраля 2022 г.
- ^ Далтон, Джон (1801). «Очерк II. О силе пара или пара из воды и различных других жидкостей как в вакууме, так и на воздухе» . Мемуары Литературно-философского общества Манчестера . 5 часть 2: 550–574.
- ^ Далтон, Джон (1801). «Очерк IV. О расширении упругих жидкостей при нагревании» . Мемуары Литературно-философского общества Манчестера . 5 часть 2: 595–602.
- ^ Гей-Люссак, Жозеф Луи (1802), «Исследование расширения газов и паров», Annales de Chimie , XLIII : 137 . Английский перевод (отрывок).
- ^ Томсон 1882 , стр. 100–106.
- ^ Перейти обратно: а б Мэги, Уильям Фрэнсис (1935). Справочник по физике . п. 237.
- ^ Томсон 1882 , с. 104: «Если мы продвинем строгий принцип градуировки, изложенный выше, достаточно далеко, мы должны прийти к точке, соответствующей уменьшению объема воздуха до нуля, что будет отмечено как -273 ° шкалы (-100 / ·366, если ·366 — коэффициент расширения); и, следовательно, —273° воздушного термометра — это точка, которой нельзя достичь ни при какой конечной температуре, какой бы низкой она ни была».
- ^ Томсон 1882 , с. 104.
- ^ Томсон 1882 , с. 187.
- ^ Перейти обратно: а б Томсон 1882 , с. 106.
- ^ Томсон 1882 , с. 193.
- ^ Томсон 1882 , с. 212.
- ^ Томсон 1882 , с. 186.
- ^ Томсон 1882 , с. 192.
- ^ Томсон 1882 , стр. 214–215.
- ^ Томсон 1882 , с. 213.
- ^ Томсон 1882 , с. 388.
- ^ Томсон 1882 , с. 105: «Произвольные точки, совпадающие на двух шкалах, равны 0° и 100°».
- ^ Саслоу, ВМ (07 января 2020 г.). «История термодинамики: недостающее руководство» . Энтропия . 22 (1). уравнение (36). Бибкод : 2020Entrp..22...77S . дои : 10.3390/e22010077 . ПМК 7516509 . PMID 33285852 .
- ^ Томсон 1882 , с. 190, формула (7).
- ^ Томсон 1882 , стр. 106, 232–236.
- ^ Томсон 1882 , с. 234.
- ^ Ван, Линь-Шу (2020). Трактат о тепле и энергии . Чам: Спрингер. п. 77. ИСБН 9783030057466 .
- ^ Томсон 1882 , с. 235.
- ^ Томсон 1882 , с. 236.
- ^ Томсон, Джеймс (1873). «Количественное исследование некоторых отношений между газообразным, жидким и твердым состояниями водного вещества» . Труды Лондонского королевского общества . 22 : 28. Бибкод : 1873RSPS...22...27T . ISSN 0370-1662 .
и, следовательно, три кривые встретились бы или пересеклись друг с другом в одной точке, которую я назвал тройной точкой .
- ^ Перейти обратно: а б Суинтон, Флорида (сентябрь 1967 г.). «Тройная точка воды» . Журнал химического образования . 44 (9): 541. Бибкод : 1967ЖЧЭд..44..541С . дои : 10.1021/ed044p541 . ISSN 0021-9584 .
- ^ «Резолюция 3 9-й ГКМВ (1948 г.)» . БИПМ . Проверено 21 февраля 2022 г.
- ^ «Резолюция 3 10-й ГКМВ (1954 г.)» . БИПМ . Проверено 21 февраля 2022 г.
- ^ «Резолюция 3: Определение термодинамической температурной шкалы» . Резолюции 10-й ГКМВ . Международное бюро мер и веса. 1954. Архивировано из оригинала 23 июня 2007 г. Проверено 6 февраля 2008 г.
- ^ Перейти обратно: а б «Резолюция 3 13-й ГКМВ (1967 г.)» . БИПМ . Проверено 21 февраля 2022 г.
- ^ «Резолюция 3: единица термодинамической температуры СИ (кельвин)» . Резолюции 13-й ГКМВ . Международное бюро мер и веса. 1967. Архивировано из оригинала 21 апреля 2007 г. Проверено 6 февраля 2008 г.
- ^ Вестфаль, Вильгельм Генрих (1952). «Нокс, темная яркость, скот» . В Вестфале, Вильгельм Х. (ред.). Физический словарь (на немецком языке) (1-е изд.). Берлин / Геттинген / Гейдельберг, Германия: Springer-Verlag OHG . стр. 125, 271, 389. doi : 10.1007/978-3-662-12706-3 . ISBN 978-3-662-12707-0 . Проверено 16 марта 2023 г. стр. 271, 389:
Яркость в темноте. [...] На основе этой кривой чувствительности в Германии в 1940 году была установлена темновая яркость с помощью единицы Скот (ск) так, что для света с цветовой температурой 2360° К 1 ск = 10 −3 асб применяется. В 1948 году Международная комиссия по освещению (IBK) установила эталонную температуру на уровне 2046°К, температуры затвердевания платины . Термин скот не был принят ИБК, но его следует называть «скотопический стильб». В Германии в качестве максимально допустимого предела темновой яркости установлено 10 шот, чтобы избежать использования темновой яркости в области смешанного колбочного и палочечного зрения , так как в этой области фотометрические измерения теряют смысл из-за постепенного скольжения кривая чувствительности глаз. [...] Скот, сокращенно sk, единица темновой яркости, которая в 1940 году Немецким светотехническим обществом была создана излучение черного тела при Т = 2360 °К, т. е. излучение с цветовой температурой Т 1 для числовой информации и для соединения темной яркости с нормальной яркостью. Для этой связи было согласовано = 2360 °К. Источник света излучает темновую яркость 1 ск, если она фотометрически равна излучению цветовой температуры. Т 2 = 2360 °К и яркость 10 −3 асб (апостиль). При цветовой температуре T 1 = 2360 °К справедливо соотношение: 1 sk = 10. −3 пожалуйста = 10 −7 /п сб.
- ^ «Резолюция 4 13-й ГКМВ (1967 г.)» . БИПМ . Проверено 21 февраля 2022 г.
- ^ «Резолюция 4: Определение единицы термодинамической температуры СИ (кельвин)» . Резолюции 13-й ГКМВ . Международное бюро мер и веса. 1967. Архивировано из оригинала 15 июня 2007 г. Проверено 6 февраля 2008 г.
- ^ «Резолюция 10 23-й ГКМВ (2007 г.)» . БИПМ . Проверено 21 февраля 2022 г.
- ^ «Единица термодинамической температуры (кельвин)» . Брошюра SI, 8-е издание . Международное бюро мер и веса. 1967. Раздел 2.1.1.5. Архивировано из оригинала 26 сентября 2007 г. Проверено 6 февраля 2008 г.
- ^ Перейти обратно: а б Ян Миллс (29 сентября 2010 г.). «Проект главы 2 брошюры SI с учетом переопределения базовых единиц» (PDF) . БИПМ . ККУ. Архивировано из оригинала (PDF) 10 января 2011 г. Проверено 1 января 2011 г.
- ^ «Генеральная конференция мер и весов одобряет возможные изменения в Международной системе единиц, включая новое определение килограмма» (PDF) (Пресс-релиз). Севр, Франция: Генеральная конференция по мерам и весам . 23 октября 2011 г. Архивировано из оригинала (PDF) 9 февраля 2012 г. Проверено 25 октября 2011 г.
- ^ Вуд, Б. (3–4 ноября 2014 г.). «Отчет о заседании целевой группы CODATA по фундаментальным константам» (PDF) . БИПМ . п. 7. Архивировано из оригинала (PDF) 13 октября 2015 г.
[Директор BIPM Мартин] Милтон ответил на вопрос о том, что произойдет, если... CIPM или CGPM проголосуют за отказ от пересмотра определения SI. Он ответил, что, по его мнению, к тому времени решение двигаться вперед следует рассматривать как предрешенное решение.
- ^ «Значение CODATA 2022: постоянная Больцмана» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
- ^ Перейти обратно: а б «Резолюция 1 26-й ГКМВ (2018 г.)» . БИПМ . Проверено 21 февраля 2022 г.
- ^ Перейти обратно: а б Ньюэлл, Д.Б.; Кабиати, Ф; Фишер, Дж; Фуджи, К; Каршенбойм, С.Г.; Марголис, HS; де Мирандес, Э; Мор, П.Дж.; Нез, Ф; Пачуки, К; Куинн, Ти Джей; Тейлор, Б.Н.; Ван, М; Вуд, Б.М.; Чжан, З; и др. (Целевая группа по фундаментальным константам Комитета по данным для науки и технологий (CODATA)) (29 января 2018 г.). «Значения h , e , k и N A в CODATA 2017 для пересмотра SI» . Метрология . 55 (1): Л13–Л16. Бибкод : 2018Метро..55Л..13Н . дои : 10.1088/1681-7575/aa950a .
- ^ «Обновление определения кельвина» (PDF) . БИПМ . Архивировано из оригинала (PDF) 23 ноября 2008 г. Проверено 23 февраля 2010 г.
- ^ Фишер, Дж; Феллмут, Б; Гайзер, С; Зандт, Т; Грудь, Л; Спараски, Ф; Плиммер, доктор медицины; де Подеста, М; Андервуд, Р.; Саттон, Дж; Мачин, Г; Гавиозо, РМ; Мадонна Рипа, D; Стер, PPM; Цюй, Дж; Фэн, XJ; Чжан, Дж; Молдовер, MR; Бенц, СП; Уайт, ДР; Джанфрани, Л; Кастрильо, А; Моретти, Л; Дарке, Б; Муфаредж, Э; Даусси, К; Бриодо, С; Козлова О; Рисегари, Л; Сеговия, Джей-Джей; Мартин, MC; дель Кампо, защитник (01 апреля 2018 г.). «Проект Больцмана» . Метрология . 55 (2): Р1–Р20. Бибкод : 2018Метро..55Р...1Ф . дои : 10.1088/1681-7575/aaa790 . ПМК 6508687 . ПМИД 31080297 .
- ^ «Руководство NIST по системе СИ | Глава 9: Правила и соглашения о стиле для названий единиц правописания» , NIST SP 811 , 28 января 2016 г.,
Производная единица в английском языке обычно имеет единственное число, например, значение 3 м. 2 ·К/Вт обычно обозначается как «три квадратных метра-кельвина на ватт», а значение 3 См·м 2 /V обычно пишется как «три кулона-метра в квадрате на вольт». Однако «единая» единица может быть множественной; например, значение 5 кПа пишется как «пять килопаскалей», хотя допустимо и «пять килопаскалей». Если в таком случае, состоящем из одной единицы, число меньше единицы, то при написании единица всегда является единственной; например, 0,5 кПа пишется как «пять десятых килопаскаля».
- ^ «Определение КЕЛЬВИНА» . www.merriam-webster.com . Проверено 21 августа 2023 г.
- ^ Руководство CERN по стилю английского языка (PDF) . ЦЕРН . 2022. с. 64.
- ^ «Написание единиц измерения СИ (Метрическая система)» . НИСТ . 13 января 2010 г.
- ^ Брэди, Джеймс Э.; Сенезе, Фред (28 января 2008 г.). Химия, Учебное пособие для студентов: Изучение материи и ее изменений . Джон Уайли и сыновья. п. 15. ISBN 978-0-470-18464-6 .
- ^ «22,2». Стандарт Юникод, версия 8.0 (PDF) . Маунтин-Вью, Калифорния, США: Консорциум Unicode. Август 2015. ISBN. 978-1-936213-10-8 . Архивировано (PDF) из оригинала 6 декабря 2016 г. Проверено 6 сентября 2015 г.
Библиография
[ редактировать ]- Международное бюро мер и веса (2019). «Брошюра о Международной системе единиц (СИ)» (PDF) . 9-е издание. Международный комитет мер и весов . Проверено 28 апреля 2022 г.
- Томсон, Уильям (лорд Кельвин) (1882). Математические и физические статьи: Том I. Издательство Кембриджского университета.
Внешние ссылки
[ редактировать ]- Томсон, Уильям (октябрь 1848 г.). «По абсолютной термометрической шкале, основанной на теории движущей силы тепла Карно и рассчитанной на основе наблюдений Рено» . zapatopi.net . Философский журнал. Архивировано из оригинала 1 февраля 2008 г. Проверено 21 февраля 2022 г.
- Томсон, Уильям (март 1851 г.). «О динамической теории тепла с численными результатами, полученными на основе эквивалента тепловой единицы г-на Джоуля, и наблюдений г-на Рено над паром» . zapatopi.net . Труды Королевского общества Эдинбурга . Проверено 5 мая 2024 г.





















