Временная логика

В логике . темпоральная логика — это любая система правил и символики для представления и рассуждения о предложениях, определяемых с точки зрения времени (например, «Я всегда голоден», «Я в конечном итоге буду голоден» или «Я буду голоден») пока я не съем что-нибудь»). Иногда его также используют для обозначения временной логики , системы темпоральной логики, основанной на модальной логике, представленной Артуром Прайором в конце 1950-х годов, с важным вкладом Ганса Кампа . В дальнейшем он был развит учёными-компьютерщиками , особенно Амиром Пнуэли , и логиками .

Темпоральная логика нашла важное применение в формальной верификации , где она используется для формулирования требований к аппаратным или программным системам. Например, можно сказать, что всякий раз, когда делается запрос, доступ к ресурсу в конечном итоге предоставляется, но он никогда не предоставляется двум запрашивающим сторонам одновременно. Такое утверждение удобно выразить во временной логике.

Мотивация

Рассмотрим утверждение «Я голоден». Хотя его значение является постоянным во времени, истинностное значение утверждения может меняться со временем. Иногда это правда, а иногда ложь, но никогда одновременно истина и ложь. Во временной логике утверждение может иметь истинностное значение, которое меняется во времени, в отличие от вневременной логики, которая применяется только к утверждениям, истинностные значения которых постоянны во времени. Такая трактовка истинностного значения во времени отличает темпоральную логику от вычислительной глагольной логики .

Темпоральная логика всегда способна рассуждать о временной шкале. Так называемая логика «линейного времени» ограничивается этим типом рассуждений. Однако логика времени ветвления может рассуждать о нескольких временных шкалах. Это позволяет, в частности, относиться к средам, которые могут действовать непредсказуемо.Продолжая пример, в логике времени ветвления мы можем заявить, что «есть вероятность, что я останусь голодным навсегда» и что «существует вероятность того, что в конечном итоге я перестану быть голодным». Если мы не знаем, будем ли меня когда-нибудь кормить, оба этих утверждения могут быть правдой.

История

Хотя логика Аристотеля почти полностью связана с теорией категорического силлогизма , в его работах есть отрывки, которые сейчас рассматриваются как предвосхищение темпоральной логики и могут подразумевать раннюю, частично развитую форму первого порядка темпоральной модальной двухвалентной логики . . Аристотель был особенно озабочен проблемой будущих контингентов , где он не мог согласиться с тем, что принцип бивалентности применим к утверждениям о будущих событиях, т.е. что мы можем в настоящий момент решить, является ли утверждение о будущем событии истинным или ложным, например, «существует завтра будет морской бой».

На протяжении тысячелетий развития не было, как отмечал Чарльз Сандерс Пирс в 19 веке:

Логики обычно рассматривают время как так называемую «экстралогическую» материю. Я никогда не разделял этого мнения. Но я думал, что логика еще не достигла того состояния развития, на котором введение временных изменений ее форм не привело бы к большой путанице; и я пока придерживаюсь такого же образа мышления.

К удивлению Пирса , первая система темпоральной логики была построена, насколько нам известно, в первой половине 20 века. Хотя Артур Прайор широко известен как основатель темпоральной логики, первая формализация такой логики была предоставлена ​​в 1947 году польским логиком Ежи Лось . В своей работе Podstawy Analizy Metodologicznej Kanonów Milla ( «Основы методологического анализа методов Милля ») он представил формализацию канонов Милля . В подходе Лось акцент был сделан на факторе времени. Таким образом, чтобы достичь своей цели, ему пришлось создать логику, которая могла бы предоставить средства формализации временных функций. Эту логику можно рассматривать как побочный продукт главной цели Лося . хотя это была первая позиционная логика, которая в качестве основы позже использовалась для Лося изобретений в эпистемической логике . Сама логика имеет синтаксис, сильно отличающийся от временной логики Прайора, в которой используются модальные операторы. Язык логики Лось скорее использует оператор реализации, специфичный для позиционной логики, который связывает выражение с конкретным контекстом, в котором рассматривается его истинностное значение. В творчестве Лося этот рассматриваемый контекст был лишь временным, поэтому выражения были связаны с конкретными моментами или интервалами времени.

В последующие годы начались исследования темпоральной логики Артура Прайора . Его волновали философские последствия свободы воли и предопределения . По словам его жены, он впервые задумался о формализации темпоральной логики в 1953 году. Результаты его исследований были впервые представлены на конференции в Веллингтоне в 1954 году. Система, представленная Прайором, была синтаксически похожа на логику Лося , хотя только в 1955 году он явно ссылался на работу Лося Прайора в последнем разделе Приложения 1 в «Формальной логике» .

Прайор читал лекции по этой теме в Оксфордском университете в 1955–1956 годах, а в 1957 году опубликовал книгу « Время и модальность» , в которой он представил пропозициональную модальную логику с двумя временными связками ( модальными операторами ), F и P, соответствующими «когда-нибудь в будущем» и «когда-нибудь в прошлом». В этой ранней работе Прайор считал время линейным. Однако в 1958 году он получил письмо от Саула Крипке , который указывал, что это предположение, возможно, необоснованно. В развитии, которое предвещало подобное развитие в информатике, Прайор принял это во внимание и разработал две теории ветвления времени, которые он назвал «оккамистской» и «пирсианской». Между 1958 и 1965 годами Прайор также переписывался с Чарльзом Леонардом Хэмблином , и в этой переписке можно проследить ряд ранних событий в этой области, например, последствия Хэмблина . Прайор опубликовал свою самую зрелую работу по этой теме - книгу « Прошлое, настоящее и будущее» в 1967 году. Он умер два года спустя.

Наряду с временной логикой Прайор построил несколько систем позиционной логики, унаследовавших свои основные идеи от Лося . Работы в области позиционно-темпоральной логики продолжил Николас Решер в 60-70-х годах. В таких работах, как «Записки о хронологической логике» (1966), «О логике хронологических высказываний» (1968) , «Топологическая логика» (1968) и «Темпоральная логика» (1971), он исследовал связи между Лося и Приора системами . Более того, он доказал, что временные операторы Прайора могут быть определены с использованием оператора реализации в конкретной позиционной логике. Решер в своей работе создал и более общие системы позиционной логики. Хотя первые из них были созданы исключительно для временных целей, он предложил термин топологическая логика для логик, которые должны были содержать оператор реализации, но не имели конкретных темпоральных аксиом, таких как аксиома часов.

Бинарные временные операторы «С тех пор» и «До» были введены Гансом Кампом в его докторской диссертации 1968 года. диссертация, которая также содержит важный результат, связывающий темпоральную логику с логикой первого порядка — результат, теперь известный как теорема Кампа .

Двумя ранними претендентами на формальные проверки были линейная временная логика , логика линейного времени Амира Пнуэли , и логика дерева вычислений (CTL), логика времени ветвления Мордехая Бен-Ари , Зохара Манны и Амира Пнуэли. Почти эквивалентный формализм CTL был предложен примерно в то же время Э.М. Кларком и Э.А. Эмерсоном . Тот факт, что вторая логика может быть решена более эффективно, чем первая, не отражается на логике ветвления и линейного времени в целом, как это иногда утверждается. Скорее, Эмерсон и Лей показывают, что любая логика линейного времени может быть расширена до логики времени ветвления, решение которой может быть выполнено с той же сложностью.

Позиционная логика Лося

Логика Лося была опубликована в качестве его магистерской диссертации в 1947 году «Podstawy Analizy Metodologicznej Kanonów Milla» ( «Основы методологического анализа методов Милля» ). Его философские и формальные концепции можно рассматривать как продолжение идей Львовско -Варшавской школы логики , поскольку его руководителем был Ежи Слупецкий , ученик Яна Лукасевича . Статья не была переведена на английский язык до 1977 года, хотя Генрик Хиж представил в 1951 году краткий, но информативный обзор в « Журнале символической логики» . Этот обзор содержал основные концепции работы Лося и был достаточен для популяризации его результатов среди логического сообщества. Основной целью данной работы было представить каноны Милля в рамках формальной логики. Для достижения этой цели автор исследовал значение темпоральных функций в структуре концепции Милля. Имея это, он предложил свою аксиоматическую систему логики, которая могла бы послужить основой для канонов Милля вместе с их временными аспектами.

Синтаксис

Язык логики, впервые опубликованный в Podstawy Analizy Metodologicznej Kanonów Milla ( «Основы методологического анализа методов Милля »), состоял из:

• логические операторы первого порядка '¬', '∧', '∨', '→', '≡', '∀' и '∃'
• оператор реализации U
• функциональный символ δ
• пропозициональные переменные p ₁ ,p ₂ ,p ₃ ,...
• переменные, обозначающие моменты времени t ₁ ,t ₂ ,t ₃ ,...
• переменные, обозначающие временные интервалы n ₁ ,n ₂ ,n ₃ ,...

Множество термов (обозначается S) строится следующим образом:

• переменные, обозначающие моменты времени или интервалы, являются термовами
• если $\tau \in S$ и $\epsilon$ является переменной временного интервала, тогда $\delta (\tau ,\epsilon )\in S$

Набор формул (обозначается For) строится следующим образом:

• все логические формулы первого порядка действительны
• если $\tau \in S$ и $\phi$ является пропозициональной переменной, то $U_{\tau }(\phi )\in For$
• если $\phi \in For$, затем $\neg \phi \in For$
• если $\phi ,\psi \in For$ и $\circ \in \{\wedge ,\vee ,\rightarrow ,\equiv \}$, затем $\phi \circ \psi \in For$
• если $\phi \in For$ и $Q\in \{\forall ,\exists \}$ и υ — пропозициональная, моментная или интервальная переменная, тогда $Q_{\upsilon }\phi \in For$

Оригинальная аксиоматическая система

1. $U_{t_{1}}\neg p_{1}\equiv \neg U_{t_{1}}p_{1}$
2. $U_{t_{1}}(p_{1}\rightarrow p_{2})\rightarrow (U_{t_{1}}p_{1}\rightarrow U_{t_{1}}p_{2})$
3. $U_{t_{1}}((p_{1}\rightarrow p_{2})\rightarrow ((p_{2}\rightarrow p_{3})\rightarrow (p_{1}\rightarrow p_{3})))$
4. $U_{t_{1}}(p_{1}\rightarrow (\neg p_{1}\rightarrow p_{2}))$
5. $U_{t_{1}}((\neg p_{1}\rightarrow p_{1})\rightarrow p_{1})$
6. $\forall _{t_{1}}U_{t_{1}}p_{1}\rightarrow p_{1}$
7. $\forall _{t_{1}}\forall _{n_{1}}\exists _{t_{2}}\forall _{p_{1}}(U_{\delta (t_{1},n_{1})}p_{1}\equiv U_{t_{2}}p_{1})$
8. $\forall _{t_{1}}\forall _{n_{1}}\exists _{t_{2}}\forall _{p_{1}}(U_{\delta (t_{2},n_{1})}p_{1}\equiv U_{t_{1}}p_{1})$
9. $\forall _{t_{1}}\exists _{p_{1}}\forall _{t_{2}}(U_{t_{2}}p_{1}\equiv \forall _{p_{2}}(U_{t_{1}}p_{2}\equiv U_{t_{2}}p_{2}))$

Напряженная логика Прайора (TL)

Логика временного предложения, представленная в книге «Время и модальность», имеет четыре (не- истинно-функциональных ) модальных оператора (в дополнение ко всем обычным функциональным истинности операторам в логике высказываний первого порядка ).

• П : «Было так, что...» (П означает «прошлое»).
• Ф : «Будет так, что...» (F означает «будущее»).
• Г : «Так будет всегда…»
• Х : «Так всегда было…»

Их можно объединить, если мы позволим π быть бесконечным путем:

• $\pi \vDash FG\phi$: «В какой-то момент $\phi$ верно во всех будущих состояниях пути»
• $\pi \vDash GF\phi$: " $\phi$ верно в бесконечном числе состояний на пути»

Из P и F можно определить G и H , и наоборот:

${\begin{aligned}F&\equiv \lnot G\lnot \\P&\equiv \lnot H\lnot \end{aligned}}$

Синтаксис и семантика

Минимальный синтаксис для TL определяется следующей грамматикой BNF :

$\phi ::=a\;|\;\bot \;|\;\lnot \phi \;|\;\phi \lor \phi \;|\;G\phi \;|\;H\phi$

где a — некоторая атомарная формула .

Модели Крипке используются для оценки истинности предложений в TL. Пара ( T , <) множества T и бинарного отношения < на T (называемого «приоритетом») называется фреймом . Модель называемой задается тройкой ( T , <, V ) кадра и функцией V, оценкой , которая присваивает каждой паре ( a , u ) атомарной формулы и временного значения некоторое значение истинности. Понятие « φ истинно в модели U =( T , <, V ) в момент времени u » сокращенно обозначается U ⊨ φ [ u ]. С помощью этого обозначения

Заявление	... верно только тогда, когда
U ⊨ а [ ты ]	V ( а , ты ) = правда
U ⊨¬ φ [ ты ]	не U ⊨ φ [ ты ]
U ⊨( φ ∧ ψ )[ ты ]	U ⊨ ψ [ ты ] и U ⊨ ψ [ ты ]
U ⊨( φ ∨ ψ )[ ты ]	U ⊨ ψ [ ты ] или U ⊨ ψ [ ты ]
U ⊨( φ → ψ )[ ты ]	U ⊨ ψ [ ты ], если U ⊨ ψ [ ты ]
U ⊨G φ [ ты ]	U ⊨ φ [ v ] для всех v таких, что u < v
U ⊨H φ [ ты ]	U ⊨ φ [ v ] для всех v таких, что v < u

Учитывая класс F фреймов, предложение φ из TL является

• справедливо по отношению к F, если для каждой модели U =( T ,<, V ) с ( T ,<) в F и для каждого u в T , U ⊨ φ [ u ]
• выполнимо относительно F, если существует модель U =( T ,<, V ) с ( , <) в F такая, что для некоторого u из T U T ⊨ φ [ u ]
• следствие , предложения ψ относительно F , если для каждой модели U =( T ,<, V ) с ( T <) в F и для каждого u в T , если U ⊨ ψ [ u ], то U ⊨ φ [ ты ]

Многие предложения действительны только для ограниченного класса фреймов. Обычно класс фреймов ограничивается рамками с отношением <, которое является транзитивным , антисимметричным , рефлексивным , трихотомическим , иррефлексивным , тотальным , плотным или некоторой их комбинацией.

Минимальная аксиоматическая логика

Бёрджесс обрисовывает логику, которая не делает никаких предположений относительно отношения <, но допускает значимые выводы, основанные на следующей схеме аксиом:

1. A , где A — тавтология логики первого порядка.
2. Г( А → Б )→(Г А → ГБ )
3. ЧАС( А → Б )→( ЧА → ЧБ )
4. A →GP A
5. A →HF A

со следующими правилами вычета:

1. учитывая A → B и A , вывести B ( метод установки )
2. учитывая тавтологию A , сделать вывод G A
3. учитывая тавтологию A , сделайте вывод H A

Можно вывести следующие правила:

1. Правило Беккера : по заданному A → B вывести T A → TB, где T — время , любую последовательность, состоящую из G, H, F и P.
2. Зеркальное отображение : по теореме A выведите ее зеркальное утверждение A. ^§ , который получается заменой G на H (и, следовательно, F на P) и наоборот.
3. Двойственность : по теореме A выведите ее двойственное утверждение A *, которое получается путем замены ∧ на ∨, G на F и H на P.

Перевод в логику предикатов

Бёрджесс дает перевод Мередита из утверждений в TL в утверждения в логике первого порядка с одной свободной переменной x ₀ (представляющей настоящий момент). Этот перевод M определяется рекурсивно следующим образом:

${\begin{aligned}&M(a)&&=a^{*}x_{0}\\&M(\lnot \phi )&&=\lnot M(\phi )\\&M(\phi \land \psi )&&=M(\phi )\land M(\psi )\\&M({\mathsf {G}}\phi )&&=\forall x_{1}(x_{0}<x_{1}\rightarrow M(A^{+}))\\&M({\mathsf {H}}\phi )&&=\forall x_{1}(x_{1}<x_{0}\rightarrow M(A^{+}))\end{aligned}}$

где $A^{+}$ — это предложение A со всеми индексами переменных, увеличенными на 1, и $a^{*}$ является одноместным предикатом, определяемым $x\mapsto V(a,x)$.

Временные операторы

Темпоральная логика имеет два типа операторов: логические операторы и модальные операторы. Логические операторы — это обычные операторы с функциональными истинностями ( $\neg ,\lor ,\land ,\rightarrow$). Модальные операторы, используемые в линейной темпоральной логике и логике дерева вычислений, определяются следующим образом.

Текстовый	Символический	Определение	Объяснение	Диаграмма
Бинарные операторы
φ U ψ	$\phi ~{\mathcal {U}}~\psi$	$(B\,{\mathcal {U}}\,C)(\phi )=\ (\exists i:C(\phi _{i})\land (\forall j<i:B(\phi _{j})))$	До тех пор, пока: ψ сохраняется в текущей или будущей позиции, и φ должна сохраняться до этой позиции. В этом положении φ больше не обязана сохраняться.
φ р ψ	$\phi ~{\mathcal {R}}~\psi$	$(B\,{\mathcal {R}}\,C)(\phi )=\ (\forall i:C(\phi _{i})\lor (\exists j<i:B(\phi _{j})))$	Освобождение : φ освобождает ψ, если ψ истинно вплоть до первой позиции, в которой φ истинно (или навсегда, если такая позиция не существует).
Унарные операторы
Н φ	$\bigcirc \phi$	${\mathcal {N}}B(\phi _{i})=B(\phi _{i+1})$	N ext: φ должна сохраняться в следующем состоянии. ( X используется как синоним.)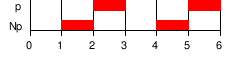
F φ	$\Diamond \phi$	${\mathcal {F}}B(\phi )=(true\,{\mathcal {U}}\,B)(\phi )$	Будущее : φ в конечном итоге должна выполняться (где-то на следующем пути).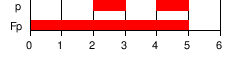
г ж	$\Box \phi$	${\mathcal {G}}B(\phi )=\neg {\mathcal {F}}\neg B(\phi )$	G глобально: φ должна соблюдаться на всем последующем пути.
и φ	$\forall \phi$	$({\mathcal {A}}B)(\psi )=\ (\forall \phi :\phi _{0}=\psi \to B(\phi ))$	A ll: φ должен выполняться на всех путях, начиная с текущего состояния.
Э ж	$\exists \phi$	$({\mathcal {E}}B)(\psi )=\ (\exists \phi :\phi _{0}=\psi \land B(\phi ))$	Существует : существует хотя бы один путь, начинающийся из текущего состояния, в котором φ выполняется .

Альтернативные символы:

• оператор R иногда обозначается V
• Оператор W является слабым оператором до тех пор, пока : $f\mathbf {W} g$ эквивалентно $f\mathbf {U} g\lor \mathbf {G} f$

Унарные операторы являются корректными формулами , если B( φ ) корректно сформированы. Бинарные операторы являются корректными формулами, если B( φ ) и C( φ ) правильно сформированы.

В некоторых логиках некоторые операторы не могут быть выражены. Например, оператор N не может быть выражен во временной логике действий .

Временная логика

Временная логика включает в себя:

• Некоторые системы позиционной логики
• Линейная темпоральная логика (LTL) темпоральная логика без ветвления временных шкал
• Временная логика дерева вычислений (CTL) с ветвящимися временными шкалами
• Интервальная темпоральная логика (ITL)
• Временная логика действий (ТЛА)
• Сигнальная временная логика (STL)
• Временная логика временных меток (TTL)
• Язык спецификации свойств (PSL)
• CTL* , который обобщает LTL и CTL
• Логика Хеннесси – Милнера (HML)
• Модальное μ-исчисление , включающее в качестве подмножества HML и CTL*
• Метрическая темпоральная логика (MTL)
• Метрическая интервальная темпоральная логика (MITL)
• Временная пропозициональная темпоральная логика (TPTL)
• Усеченная линейная временная логика (TLTL)
• Гипертемпоральная логика (HyperLTL)

Разновидностью, тесно связанной с временной, хронологической или временной логикой, является модальная логика, основанная на «топологии», «месте» или «пространственном положении».

См. также

• формализм ГПО
• Структура Крипке
• Теория автоматов
• Грамматика Хомского
• Государственная переходная система
• Расчет продолжительности (DC)
• Гибридная логика
• Темпоральная логика в проверке конечных состояний
• Язык координации Рео
• Модальная логика
• Материалы исследования: Архив Общества Макса Планка

Ссылки

• Мордехай Бен-Ари, Зоар Манна, Амир Пнуэли: Временная логика ветвления времени . ПОПЛ 1981: 164–176.
• Амир Пнуэли: Временная логика программ FOCS 1977: 46–57.
• Венема, Иде, 2001, «Временная логика», в издании Гобла Лу, « Руководство Блэквелла по философской логике» . Блэквелл.
• Э.А. Эмерсон и Чин-Лаунг Лей, « Модальность проверки модели: логика времени ветвления наносит ответный удар », в журнале Science of Computer Programming 8, стр. 275–306, 1987.
• Э.А. Эмерсон, « Временная и модальная логика », Справочник по теоретической информатике , глава 16, MIT Press, 1990 г.
• Практическое введение в PSL , Синди Эйснер, Дана Фисман
• Варди, Моше Ю. (2008). «От церкви и до PSL ». В Орне Грумберг; Хельмут Вейт (ред.). 25 лет проверки модели: история, достижения, перспективы . Спрингер. ISBN  978-3-540-69849-4 . препринт . Исторический взгляд на то, как, казалось бы, разрозненные идеи объединились в информатике и технике. (Упоминание Чёрча в названии этой статьи является отсылкой к малоизвестной статье 1957 года, в которой Чёрч предложил способ проверки оборудования.)

Дальнейшее чтение

• Питер Орстрем; Согласно Ф.В. Хасле (1995). Временная логика: от древних идей к искусственному интеллекту . Спрингер. ISBN  978-0-7923-3586-3 .

Внешние ссылки

• Стэнфордская энциклопедия философии : « Временная логика » Энтони Гальтона.
• Временная логика Иде Венемы, формальное описание синтаксиса и семантики, вопросы аксиоматизации. Рассматривая также диадические темпоральные операторы Кампа (с тех пор, пока)
• Заметки Яна Ходкинсона об играх по темпоральной логике , включая формальное описание темпоральной логики первого порядка.
• CADP – предоставляет общие средства проверки моделей для различной временной логики.
• PAT — это мощная бесплатная программа проверки моделей, проверки LTL, симулятора и проверки уточнений для CSP и его расширений (с общей переменной, массивами и широким диапазоном справедливости).