Графический конвейер

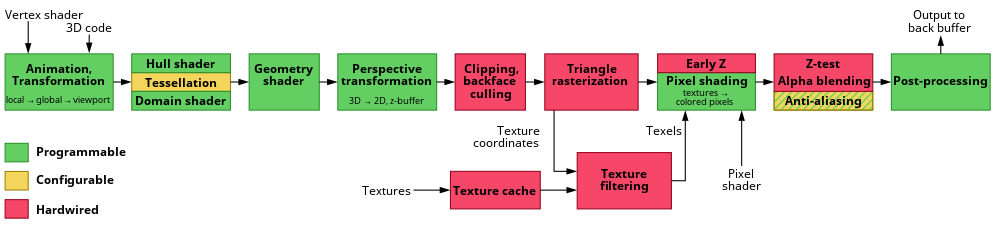
Конвейер компьютерной графики , также известный как конвейер рендеринга или графический конвейер , представляет собой структуру компьютерной графики, которая описывает необходимые процедуры для преобразования трехмерной (3D) сцены в двухмерное (2D) представление на экране. ^[1] После создания 3D-модели графический конвейер преобразует ее в визуально воспринимаемый формат на дисплее компьютера. ^[2] Из-за зависимости от конкретного программного обеспечения , аппаратных конфигураций и желаемых атрибутов отображения универсально применимого графического конвейера не существует. графических Тем не менее, интерфейсы программирования приложений (API), такие как Direct3D , OpenGL и Vulkan, были разработаны для стандартизации общих процедур и контроля графического конвейера данного аппаратного ускорителя. Эти API обеспечивают уровень абстракции над базовым оборудованием, избавляя программистов от необходимости писать код, явно ориентированный на различные аппаратные графические ускорители, такие как AMD , Intel , Nvidia и другие.

Модель графического конвейера обычно используется при рендеринге в реальном времени. Часто большинство шагов конвейера реализуются аппаратно, что позволяет проводить специальные оптимизации . Термин «конвейер» используется в аналогичном смысле для конвейера в процессорах : отдельные шаги конвейера выполняются параллельно, пока на каждом данном шаге есть то, что ему нужно.

Концепция

3D-конвейер обычно относится к наиболее распространенной форме компьютерного 3D-рендеринга, называемой 3D-рендерингом полигонов. ^{[ нужна ссылка ]}, в отличие от Raytracing и Raycasting . В методе Raycasting луч возникает в точке, где находится камера, и если этот луч попадает на поверхность, вычисляется цвет и освещение точки на поверхности, куда попадает луч. При рендеринге 3D-полигонов происходит обратный процесс: вычисляется площадь, отданная камере, а затем создаются лучи из каждой части каждой поверхности, переданной камере, и прослеживаются обратно к камере. ^[3]

Структура

Графический конвейер можно разделить на три основные части: приложение, геометрия и растеризация. ^[4]

Приложение

Шаг приложения выполняется программным обеспечением на главном процессоре ( ЦП ). На этапе приложения в сцену вносятся изменения по мере необходимости, например, при взаимодействии пользователя с использованием устройств ввода или во время анимации. Новая сцена со всеми ее примитивами (обычно треугольниками, линиями и точками) затем передается на следующий шаг конвейера.

Примерами задач, которые обычно выполняются на этапе приложения, являются методы обнаружения столкновений , анимации, морфинга и ускорения с использованием схем пространственного подразделения, таких как Quadtrees или Octrees . Они также используются для уменьшения объема оперативной памяти, необходимой в данный момент. «Мир» современной компьютерной игры гораздо больше того, что может сразу уместиться в памяти.

Геометрия

Шаг геометрии (с Geometry Pipeline ), отвечающий за большинство операций с полигонами и их вершинами (с Vertex Pipeline ), можно разделить на следующие пять задач. То, как эти задачи организованы как реальные параллельные этапы конвейера, зависит от конкретной реализации.

Определения

Вершина (множественное число: вершины) — это точка мира. Для соединения поверхностей используется множество точек. В особых случаях облака точек рисуются напрямую, но это все же исключение.

Треугольник . — самый распространенный геометрический примитив компьютерной графики Он определяется тремя вершинами и вектором нормали — вектор нормали служит для обозначения передней грани треугольника и представляет собой вектор, перпендикулярный поверхности. Треугольник может быть снабжен цветом или текстурой ( поверх него «наклеено» изображение). Треугольники предпочтительнее прямоугольников, поскольку три их точки всегда находятся в одной плоскости .

Мировая система координат

Мировая система координат — это система координат, в которой создается виртуальный мир. Это должно соответствовать нескольким условиям, чтобы можно было легко применить следующую математическую формулу:

Это должна быть прямоугольная декартова система координат, в которой все оси имеют одинаковый масштаб.

Определение единицы измерения системы координат остается на усмотрение разработчика. Таким образом, соответствует ли единичный вектор системы одному метру или ангстрему, зависит от приложения.

Будет ли использоваться правая или левая система координат, может определяться используемой графической библиотекой.

Пример: если нам нужно разработать симулятор полета, мы можем выбрать мировую систему координат так, чтобы начало координат находилось в центре Земли, а единица измерения была установлена на один метр. Кроме того, чтобы облегчить привязку к реальности, определим, что ось X должна пересекать экватор на нулевом меридиане, а ось Z проходит через полюса. В правосторонней системе ось Y проходит через меридиан 90° восточной долготы (где-то в Индийском океане ). Теперь у нас есть система координат, описывающая каждую точку Земли в трехмерных декартовых координатах . В этой системе координат мы сейчас моделируем принципы нашего мира, гор, долин и океанов.

Примечание. Помимо компьютерной геометрии, географические координаты используются для Земли , т. е. широта и долгота , а также высота над уровнем моря. Приблизительное преобразование - если не учитывать тот факт, что Земля не является точной сферой - простое:

{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}(R+{hasl})*\cos({lat})*\cos({long})\\(R+{hasl})*\cos({lat})*\sin({long})\\(R+{hasl})*\sin({lat})\end{pmatrix}}

где R = радиус Земли [6,378,137 м], широта = широта, долгота = долгота, hasl = высота над уровнем моря.

Все следующие примеры применимы в правосторонней системе. Для левосторонней системы знаки, возможно, придется поменять местами.

Объекты, содержащиеся в сцене (дома, деревья, автомобили), часто проектируются в их системе координат объекта (также называемой системой координат модели или локальной системой координат) из соображений упрощения моделирования. Чтобы присвоить этим объектам координаты в мировой системе координат или глобальной системе координат всей сцены, координаты объекта преобразуются с помощью перевода, вращения или масштабирования. Это делается путем умножения соответствующих матриц преобразования . Кроме того, из одного объекта может быть образовано несколько по-разному преобразованных копий, например, из дерева лес; Этот метод называется созданием экземпляров.

Чтобы разместить модель самолета в мире, мы сначала определяем четыре матрицы. Поскольку мы работаем в трехмерном пространстве, нам нужны четырехмерные однородные матрицы . для наших расчетов

Во-первых, нам нужны три матрицы вращения , а именно по одной на каждую из трех осей самолета (вертикальная ось, поперечная ось, продольная ось).

Вокруг оси X (обычно определяемой как продольная ось в системе координат объекта)

$R_{x}={\begin{pmatrix}1&0&0&0\\0&\cos(\alpha )&\sin(\alpha )&0\\0&-\sin(\alpha )&\cos(\alpha )&0\\0&0&0&1\end{pmatrix}}$

Вокруг оси Y (обычно определяемой как поперечная ось в системе координат объекта)

$R_{y}={\begin{pmatrix}\cos(\alpha )&0&-\sin(\alpha )&0\\0&1&0&0\\\sin(\alpha )&0&\cos(\alpha )&0\\0&0&0&1\end{pmatrix}}$

Вокруг оси Z (обычно определяемой как вертикальная ось в системе координат объекта)

$R_{z}={\begin{pmatrix}\cos(\alpha )&\sin(\alpha )&0&0\\-\sin(\alpha )&\cos(\alpha )&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}$

Мы также используем матрицу перевода, которая перемещает самолет в нужную точку нашего мира: $T_{x,y,z}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\x&y&z&1\end{pmatrix}}$ .

Примечание : Приведенные выше матрицы транспонируются относительно матриц ротации статей . Объяснение почему смотрите ниже.

Теперь мы могли вычислить положение вершин самолета в мировых координатах, последовательно умножив каждую точку на эти четыре матрицы. Поскольку умножение матрицы на вектор является довольно дорогостоящим (отнимает много времени), обычно выбирают другой путь и сначала перемножают четыре матрицы вместе. Умножение двух матриц еще более затратно, но должно выполняться только один раз для всего объекта. Умножения $((((v*R_{x})*R_{y})*R_{z})*T)$ и $(v*(((R_{x}*R_{y})*R_{z})*T))$ эквивалентны. После этого полученную матрицу можно применить к вершинам. На практике, однако, умножение на вершины пока не применяется, а сначала определяются матрицы камер (см. ниже).

Однако для нашего приведенного выше примера перевод должен определяться несколько иначе, поскольку общее значение « вверх », за исключением Северного полюса, не совпадает с нашим определением положительной оси Z, и поэтому модель также необходимо повернуть. вокруг центра Земли:

T_{Kugel}=T_{x,y,z}(0,0,R+{hasl})*R_{y}(\Pi /2-{lat})*R_{z}({long})

На первом этапе начало координат модели перемещается на правильную высоту над поверхностью Земли, затем оно поворачивается по широте и долготе.

Порядок применения матриц важен, поскольку умножение матриц является не коммутативным . Это также относится к трем вращениям, что можно продемонстрировать на примере: Точка (1, 0, 0) лежит на оси X, если повернуть ее сначала на 90° вокруг X-, а затем вокруг Y-. оси, он оказывается на оси Z (вращение вокруг оси X не влияет на точку, находящуюся на оси). С другой стороны, если сначала вращаться вокруг оси Y, а затем вокруг оси X, результирующая точка окажется на оси Y. Сама последовательность произвольна, пока она всегда одинакова. Последовательность с x, затем y, затем z (крен, тангаж, курс) часто является наиболее интуитивно понятной, поскольку вращение заставляет направление компаса совпадать с направлением «носа».

Существует также два соглашения для определения этих матриц, в зависимости от того, хотите ли вы работать с векторами-столбцами или векторами-строками. Разные графические библиотеки имеют здесь разные предпочтения. OpenGL предпочитает векторы-столбцы, векторы-строки DirectX . Решение определяет, с какой стороны точечные векторы должны быть умножены на матрицы преобразования. Для векторов-столбцов умножение выполняется справа, т.е. $v_{out}=M*v_{in}$ , где v _out и v _in — векторы-столбцы 4x1. Объединение матриц также производится справа налево, т.е., например $M=T_{x}*R_{x}$ , при первом вращении, а затем при переключении.

В случае векторов-строок это работает с точностью до наоборот. Умножение теперь происходит слева как $v_{out}=v_{in}*M$ с векторами строк размером 1x4, а конкатенация $M=R_{x}*T_{x}$ когда мы тоже сначала вращаемся, а потом движемся. Матрицы, показанные выше, действительны для второго случая, тогда как матрицы для векторов-столбцов транспонируются. Правило $(v*M)^{T}=M^{T}*v^{T}$ ^[5] применяется, что для умножения на векторы означает, что вы можете переключать порядок умножения, транспонируя матрицу.

В цепочке матриц каждое преобразование определяет новую систему координат, что позволяет гибко расширять ее. Например, пропеллер самолета, смоделированный отдельно, можно прикрепить к носовой части самолета путем перемещения, которое лишь смещается от модели к системе координат пропеллера. Чтобы визуализировать самолет, сначала вычисляется его матрица преобразования для преобразования точек, а затем умножается матрица модели пропеллера на матрицу самолета для точек пропеллера. Эта рассчитанная матрица известна как «мировая матрица», необходимая для каждого объекта в сцене перед рендерингом. Затем приложение может динамически изменять эти матрицы, например обновлять положение самолета в каждом кадре в зависимости от скорости.

Вычисленную таким образом матрицу еще называют мировой матрицей . Перед рендерингом его необходимо определить для каждого объекта в мире. Приложение может внести сюда изменения, например, меняя положение самолета в зависимости от скорости после каждого кадра.

Трансформация камеры

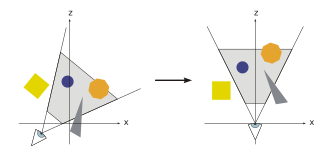
Помимо объектов, сцена также определяет виртуальную камеру или средство просмотра, которое указывает положение и направление обзора, относительно которого визуализируется сцена. Сцена преобразуется так, что камера находится в начале координат и смотрит вдоль оси Z. Результирующая система координат называется системой координат камеры, а преобразование называется преобразованием камеры или преобразованием представления .

Матрица обзора обычно определяется по положению камеры, целевой точке (куда смотрит камера) и «вектору вверх» («вверх» от точки зрения зрителя). Требуются первые три вспомогательных вектора:

Zaxis = normal(cameraPosition - cameraTarget)

Xaxis = normal(cross(cameraUpVector, Zaxis))

Yaxis = cross(Zaxis, Xaxis )

С Normal(v) = нормализация вектора v;

крест(v1, v2) = векторное произведение v1 и v2.

Наконец, матрица:

{\begin{pmatrix}{xaxis}.x&{yaxis}.x&{zaxis}.x&0\\{xaxis}.y&{yaxis}.y&{zaxis}.y&0\\{xaxis}.z&{yaxis}.z&{zaxis}.z&0\\-{dot}({xaxis},{cameraPosition})&-{dot}({yaxis},{cameraPosition})&-{dot}({zaxis},{cameraPosition})&1\end{pmatrix}}

где точка(v1, v2) = скалярное произведение v1 и v2.

Проекция

Шаг 3D-проекции преобразует объем вида в куб с координатами угловой точки (-1, -1, 0) и (1, 1, 1); Иногда используются и другие целевые тома. Этот шаг называется проекцией , хотя он преобразует один объем в другой объем, поскольку полученные координаты Z не сохраняются в изображении, а используются только в Z-буферизации на последующем этапе растрирования. На перспективной иллюстрации центральная проекция используется . Для ограничения количества отображаемых объектов используются две дополнительные плоскости отсечения; Таким образом, зрительный объем представляет собой усеченную пирамиду ( frustum ). Параллельная или ортогональная проекция используется, например, для технических изображений, поскольку она имеет то преимущество, что все параллели в пространстве объекта также параллельны в пространстве изображений, а поверхности и объемы имеют одинаковый размер независимо от расстояния от зрителя. . В картах используется, например, ортогональная проекция (так называемая ортофото ), но косые изображения ландшафта таким образом использовать нельзя — хотя технически их можно визуализировать, но они кажутся настолько искаженными, что мы не можем ими воспользоваться. Формула для расчета матрицы отображения перспективы:

${\begin{pmatrix}w&0&0&0\\0&h&0&0\\0&0&{far}/({near-far})&-1\\0&0&({near}*{far})/({near}-{far})&0\end{pmatrix}}$

С h=cot(fieldOfView/2.0) (угол раскрытия камеры); w = h/Aspect Ratio (соотношение сторон целевого изображения); ближний = наименьшее расстояние, с которого можно быть видимым; Far = Самое большое расстояние, которое будет видно.

Причины, по которым здесь необходимо указывать наименьшее и наибольшее расстояние, заключаются, с одной стороны, в том, что это расстояние разделено для достижения масштаба сцены (более удаленные объекты на перспективном изображении меньше, чем близкие), а с другой - с другой стороны, чтобы масштабировать значения Z в диапазоне 0..1 для заполнения Z-буфера . Этот буфер часто имеет разрешение всего 16 бит, поэтому значения ближнего и дальнего света следует выбирать осторожно. Слишком большая разница между ближним и дальним значением приводит к так называемой Z-борьбе из-за низкого разрешения Z-буфера. Из формулы также видно, что ближайшее значение не может быть равно 0, поскольку эта точка является точкой фокуса проекции. На данный момент изображения нет.

Для полноты картины формула параллельной проекции (ортогональной проекции):

${\begin{pmatrix}2.0/w&0&0&0\\0&2.0/h&0&0\\0&0&1.0/({near-far})&-1\\0&0&{near}/({near}-{far})&0\end{pmatrix}}$

где w = ширина целевого куба (размерность в единицах мировой системы координат); H = w/Aspect Ratio (соотношение сторон целевого изображения); ближний = наименьшее расстояние, с которого можно быть видимым; Far = самое большое расстояние, на котором можно быть видимым.

Из соображений эффективности камера и матрица проекции обычно объединяются в матрицу преобразования, так что система координат камеры опускается. Результирующая матрица обычно одинакова для одного изображения, тогда как мировая матрица выглядит по-разному для каждого объекта. Таким образом, на практике вид и проекция заранее рассчитываются так, что во время отображения необходимо адаптировать только мировую матрицу. Однако возможны более сложные преобразования, такие как смешивание вершин. Также могут быть выполнены свободно программируемые шейдеры геометрии , изменяющие геометрию.

На фактическом этапе рендеринга вычисляется мировая матрица * матрица камеры * матрица проекции, а затем, наконец, применяется к каждой отдельной точке. Таким образом, точки всех объектов переносятся непосредственно в экранную систему координат (по крайней мере почти, диапазон значений осей по-прежнему -1..1 для видимого диапазона, см. раздел «Окно-Вьюпорт-Трансформация»).

Освещение

Часто сцена содержит источники света, расположенные в разных местах, чтобы освещение объектов выглядело более реалистичным. В этом случае коэффициент усиления текстуры рассчитывается для каждой вершины на основе источников света и свойств материала, связанных с соответствующим треугольником. На более позднем этапе растеризации значения вершин треугольника интерполируются по его поверхности. Ко всем поверхностям применяется общее освещение (рассеянный свет). Это рассеянная и, следовательно, независимая от направления яркость сцены. Солнце — это направленный источник света, который можно считать бесконечно далеким. Освещенность, действующая на поверхность солнцем, определяется путем формирования скалярного произведения вектора направления от Солнца и вектора нормали к поверхности. Если значение отрицательное, поверхность обращена к солнцу.

Обрезка

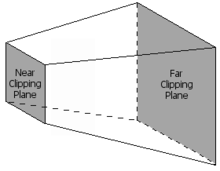
(рисовать) необходимо только примитивы, находящиеся в пределах визуального объема Растрировать . Этот визуальный объем определяется как внутренняя часть усеченной пирамиды , формы в виде пирамиды со срезанной вершиной. Примитивы, полностью находящиеся за пределами визуального объема, отбрасываются; Это называется отбраковкой усеченного конуса . Дальнейшие методы отбора, такие как обратный отбор, который уменьшает количество рассматриваемых примитивов, теоретически могут быть выполнены на любом этапе графического конвейера. Примитивы, которые лишь частично находятся внутри куба, должны быть обрезаны по кубу. Преимущество предыдущего шага проецирования состоит в том, что отсечение всегда происходит по одному и тому же кубу. На последний шаг передаются только примитивы (возможно, обрезанные), находящиеся в пределах визуального объема.

Преобразование «Окно-Вьюпорт»

Чтобы вывести изображение в любую целевую область (окно просмотра) экрана, другое преобразование — преобразование «Окно-Вьюпорт» необходимо применить . Это сдвиг, за которым следует масштабирование. Полученные координаты являются координатами устройства вывода. Окно просмотра содержит 6 значений: высоту и ширину окна в пикселях, верхний левый угол окна в координатах окна (обычно 0, 0), а также минимальное и максимальное значения Z (обычно 0 и 1).

Формально:

{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}{vp}.X+(1.0+v.X)*{vp}.{width}/2.0\\{vp}.Y+(1.0-v.Y)*{vp}.{height}/2.0\\{vp}.{minz}+v.Z*({vp}.{maxz}-{vp}.{minz})\end{pmatrix}}

С vp=Viewport; v=Точка после проекции

На современном оборудовании большая часть шагов вычисления геометрии выполняется в вершинном шейдере . Это, в принципе, свободно программируется, но обычно выполняет как минимум преобразование точек и расчет освещенности. Для интерфейса программирования DirectX начиная с версии 10 необходимо использование собственного вершинного шейдера, тогда как в более старых версиях все еще есть стандартный шейдер.

Растеризация

Шаг растеризации — это последний шаг перед конвейером фрагментного шейдера, с помощью которого растеризуются все примитивы . На этапе растеризации из непрерывных примитивов создаются дискретные фрагменты.

На этом этапе графического конвейера точки сетки также называются фрагментами для большей различимости. Каждый фрагмент соответствует одному пикселю в буфере кадра, а это соответствует одному пикселю экрана. Они могут быть цветными (и, возможно, с подсветкой). Кроме того, необходимо определить видимый, ближайший к наблюдателю фрагмент в случае перекрывающихся полигонов. Для определения так называемой скрытой поверхности обычно используется Z-буфер . Цвет фрагмента зависит от освещения, текстуры и других свойств материала видимого примитива и часто интерполируется с использованием свойств вершины треугольника. Там, где это возможно, фрагментный шейдер (также называемый пиксельным шейдером ) запускается на этапе растра для каждого фрагмента объекта. Если фрагмент виден, его теперь можно смешать с уже существующими значениями цвета в изображении, если используется прозрачность или множественная выборка. На этом этапе один или несколько фрагментов становятся пикселями.

Чтобы пользователь не видел постепенной растеризации примитивов, происходит двойная буферизация. Растеризация осуществляется в специальной области памяти. После полной растеризации изображения оно копируется в видимую область памяти изображений.

Обратный

Все используемые матрицы невырождены и, следовательно, обратимы. Поскольку умножение двух неособых матриц создает еще одну неособую матрицу, вся матрица преобразования также обратима. Обратное требуется для пересчета мировых координат из экранных координат - например, для определения по положению указателя мыши объекта, по которому щелкнули. Однако, поскольку экран и мышь имеют только два измерения, третье неизвестно. Поэтому в месте положения курсора проецируется луч в мир и затем определяется пересечение этого луча с полигонами в мире.

Шейдер

Классические видеокарты все еще относительно близки к графическому конвейеру. С ростом требований к графическому процессору ограничения постепенно снимались, чтобы обеспечить большую гибкость. Современные видеокарты используют свободно программируемый конвейер, управляемый шейдерами, который обеспечивает прямой доступ к отдельным этапам обработки. Чтобы разгрузить основной процессор, дополнительные этапы обработки были перенесены на конвейер и графический процессор.

Наиболее важными модулями шейдеров являются вершинные шейдеры , геометрические шейдеры и пиксельные шейдеры.

юнитов . Был введен унифицированный шейдер, позволяющий в полной мере использовать преимущества всех Это дает один большой пул шейдерных блоков. По мере необходимости пул делится на разные группы шейдеров. Поэтому строгое разделение типов шейдеров больше не имеет смысла.

Также можно использовать так называемый вычислительный шейдер для выполнения любых вычислений без отображения графики на графическом процессоре. Преимущество в том, что они работают очень параллельно, но есть ограничения. Эти универсальные вычисления также называются вычислениями общего назначения на графических процессорах , или GPGPU сокращенно .

Сетчатые шейдеры — это недавнее дополнение, призванное преодолеть узкие места фиксированной компоновки геометрического конвейера. ^[6]

См. также

Источники

Акенине-Мёллер, Томас; Хейнс, Эрик; Хоффман, Нати (2019) [2008]. Рендеринг в реальном времени . ЦРК Пресс. ISBN 9781315362007 .
Бендер, Майкл; Брилл, Манфред (2006). Компьютерная графика: прикладно-ориентированный учебник . Мюнхен: Хансер. ISBN 3-446-40434-1 .
Фишер, Мартин (4 июля 2011 г.). Пиксельная фабрика. Как графические чипы создают на экране игровые миры . c't журнал о компьютерных технологиях. Издатель журнала Heise. п. 180. ISSN 0724-8679 .

Ссылки

^ «Графический конвейер» . Майкрософт . 30 мая 2018 года . Проверено 15 июня 2015 г.
^ «Лекция: Графический конвейер и анимация» . Архивировано из оригинала 7 декабря 2017 года . Проверено 15 июня 2015 г.
^ Лоуренс, Джейсон (22 октября 2012 г.). «Конвейер рендеринга 3D-полигонов» (PDF) . Архивировано (PDF) из оригинала 29 декабря 2016 г. Проверено 19 сентября 2019 г.
^ Акенин-Мёллер, Haines & Hoffman 2019 , стр. 13 2.1 Архитектура Рисунок 2.2
^ Нипп, К.; Стоффер, Д. (1998). Линейная алгебра . v/d/f Издательство ETH Zurich University Press. ISBN 3-7281-2649-7 .
^ Расширенная производительность API: сетчатые шейдеры

Внешние ссылки

^{[ мертвая ссылка ]}

[1] «Графический конвейер» . Майкрософт . 30 мая 2018 года . Проверено 15 июня 2015 г.

[2] «Лекция: Графический конвейер и анимация» . Архивировано из оригинала 7 декабря 2017 года . Проверено 15 июня 2015 г.

[prince12-3] Лоуренс, Джейсон (22 октября 2012 г.). «Конвейер рендеринга 3D-полигонов» (PDF) . Архивировано (PDF) из оригинала 29 декабря 2016 г. Проверено 19 сентября 2019 г.

[4] Акенин-Мёллер, Haines & Hoffman 2019 , стр. 13 2.1 Архитектура Рисунок 2.2

[5] Нипп, К.; Стоффер, Д. (1998). Линейная алгебра . v/d/f Издательство ETH Zurich University Press. ISBN 3-7281-2649-7 .

[6] Расширенная производительность API: сетчатые шейдеры

[1]

[2]

[3]

[4]

[5]

[6]