Вибрация струн

Вибрация, стоячие волны в струне. Основной 5 и первые обертонов гармонического ряда .

Вибрация ​ струны – это волна . Резонанс заставляет колеблющуюся струну производить звук постоянной частоты , то есть постоянной высоты . Если длина и натяжение струны отрегулированы правильно, издаваемый звук представляет собой музыкальный тон . Вибрирующие струны являются основой струнных инструментов, таких как гитары , виолончели и фортепиано .

Волна

Скорость распространения волны в струне ( $v$) пропорциональна квадратному корню из силы натяжения струны ( $T$) и обратно пропорциональна квадратному корню из линейной плотности ( $\mu$) строки:

$v={\sqrt {T \over \mu }}.$

Эту связь обнаружил Винченцо Галилей в конце 1500-х годов.

Вывод

Illustration for a vibrating string

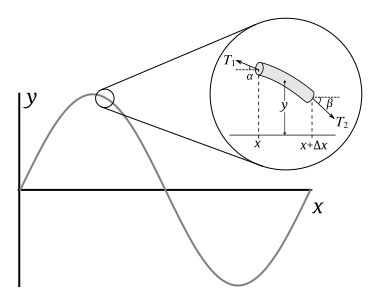
Источник:

Позволять $\Delta x$ быть длиной куска веревки, $m$ его масса и $\mu$ его линейная плотность . Если углы $\alpha$ и $\beta$ малы, то горизонтальные компоненты напряжения с обеих сторон могут быть аппроксимированы постоянными $T$, для которого результирующая горизонтальная сила равна нулю. Соответственно, используя приближение малых углов, горизонтальные напряжения, действующие по обе стороны сегмента струны, определяются выражением

$T_{1x}=T_{1}\cos(\alpha )\approx T.$

$T_{2x}=T_{2}\cos(\beta )\approx T.$

Из второго закона Ньютона для вертикальной составляющей масса (которая является произведением его линейной плотности и длины) этого куска, умноженная на его ускорение: $a$, будет равна результирующей силе, действующей на деталь:

$\Sigma F_{y}=T_{1y}-T_{2y}=-T_{2}\sin(\beta )+T_{1}\sin(\alpha )=\Delta ma\approx \mu \Delta x{\frac {\partial ^{2}y}{\partial t^{2}}}.$

Разделив это выражение на $T$ и подставляя первое и второе уравнения, получаем (мы можем выбрать либо первое, либо второе уравнение для $T$, поэтому нам удобно выбирать каждый из них с соответствующим углом $\beta$ и $\alpha$)

$-{\frac {T_{2}\sin(\beta )}{T_{2}\cos(\beta )}}+{\frac {T_{1}\sin(\alpha )}{T_{1}\cos(\alpha )}}=-\tan(\beta )+\tan(\alpha )={\frac {\mu \Delta x}{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.$

Согласно малоугловому приближению тангенсы углов на концах отрезка струны равны наклонам на концах с дополнительным знаком минус, обусловленным определением $\alpha$ и $\beta$. Использование этого факта и перестановка обеспечивают

${\frac {1}{\Delta x}}\left(\left.{\frac {\partial y}{\partial x}}\right|^{x+\Delta x}-\left.{\frac {\partial y}{\partial x}}\right|^{x}\right)={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.$

В том пределе, что $\Delta x$ приближается к нулю, левая часть представляет собой определение второй производной $y$:

${\frac {\partial ^{2}y}{\partial x^{2}}}={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.$

Это волновое уравнение для $y(x,t)$, а коэффициент при второй производной по времени равен ${\frac {1}{v^{2}}}$; таким образом

$v={\sqrt {T \over \mu }},$

Где $v$ — скорость распространения волны в струне ( см. в статье о волновом уравнении подробнее об этом ). Однако этот вывод справедлив только для колебаний малой амплитуды; для тех, которые имеют большую амплитуду, $\Delta x$ не является хорошим приближением длины куска струны, горизонтальная составляющая натяжения не обязательно постоянна. Горизонтальные напряжения плохо аппроксимируются $T$.

Частота волны

Зная скорость распространения, можно вычислить частоту звука, издаваемого струной. Скорость распространения волны равна длине волны $\lambda$ разделить на период $\tau$, или умноженный на частоту $f$:

$v={\frac {\lambda }{\tau }}=\lambda f.$

Если длина строки $L$, основная гармоника – это та, которая создается вибрацией, узлами которой являются два конца струны, поэтому $L$ равна половине длины волны основной гармоники. Отсюда следуют законы Мерсенна :

$f={\frac {v}{2L}}={1 \over 2L}{\sqrt {T \over \mu }}$

где $T$ - напряжение (в Ньютонах), $\mu$ - линейная плотность (то есть масса на единицу длины), а $L$ длина колеблющейся части струны. Поэтому:

• чем короче струна, тем выше частота основного тона
• чем выше напряжение, тем выше частота основного
• чем легче струна, тем выше частота основного тона

Более того, если мы возьмем n-ю гармонику как имеющую длину волны, определяемую выражением $\lambda _{n}=2L/n$, то мы легко получаем выражение для частоты n-й гармоники:

$f_{n}={\frac {nv}{2L}}$

А для струны, находящейся под натяжением Т с линейной плотностью $\mu$, затем

$f_{n}={\frac {n}{2L}}{\sqrt {\frac {T}{\mu }}}$

Наблюдение за колебаниями струн

Можно увидеть формы сигналов на вибрирующей струне, если частота достаточно низкая и вибрирующая струна находится перед экраном ЭЛТ, например, на телевизоре или компьютере ( не аналоговом осциллографе).Этот эффект называется стробоскопическим эффектом , и скорость, с которой кажется, что струна вибрирует, представляет собой разницу между частотой струны и частотой обновления экрана. То же самое может произойти с люминесцентной лампой со скоростью, равной разнице между частотой струны и частотой переменного тока .(Если частота обновления экрана равна частоте строки или целому кратному ей числу, строка будет выглядеть неподвижной, но деформированной.)При дневном свете и других неколеблющихся источниках света этот эффект не возникает, и струна кажется неподвижной, но более толстой, более светлой или размытой из-за постоянства зрения .

Аналогичный, но более контролируемый эффект можно получить с помощью стробоскопа . Это устройство позволяет согласовать частоту ксеноновой лампы-вспышки с частотой вибрации струны. В темной комнате отчетливо видна форма сигнала. В противном случае можно использовать изгиб или, что, возможно, проще, регулируя головки машины, чтобы получить ту же или кратную частоту переменного тока для достижения того же эффекта. Например, в случае гитары шестая (самая низкая) струна, прижатая к третьему ладу, дает соль на частоте 97,999 Гц. Небольшая регулировка может изменить ее до 100 Гц, что ровно на одну октаву выше частоты переменного тока в Европе и большинстве стран Африки и Азии, 50 Гц. В большинстве стран Америки, где частота переменного тока составляет 60 Гц, изменение частоты A# на пятой струне первого лада со 116,54 Гц на 120 Гц дает аналогичный эффект.

Реальный пример

См. Также: Настройки гитары , 12 равнотемперированных и A440 (стандарт высоты тона).

Professional Soloist XL пользователя Википедии Jackson Электрогитара порожка имеет расстояние от до подставки (соответствует $L$ выше) из 25 5 ⁄ 8 дюйма и D'Addario Струны для электрогитары сверхлегкого калибра XL с никелированной обмоткой EXL-120 со следующими характеристиками производителя:

Технические характеристики производителя D'Addario EXL-120

Номер строки.	Толщина [дюймы] ( $d$)	Рекомендуемое натяжение [фунты] ( $T$)	$\rho$ [г/см 3 ]
1	0.00899	13.1	7.726 (стальной сплав)
2	0.0110	11.0	"
3	0.0160	14.7	"
4	0.0241	15.8	6.533 (сплав никелевой стали)
5	0.0322	15.8	"
6	0.0416	14.8	"

Учитывая приведенные выше характеристики, каковы будут вычисленные частоты вибрации ( $f$) основных гармоник вышеуказанных струн, если бы струны были натянуты с натяжением, рекомендованным производителем?

Чтобы ответить на этот вопрос, мы можем начать с формулы из предыдущего раздела: $n=1$:

$f={\frac {1}{2L}}{\sqrt {\frac {T}{\mu }}}$

Линейная плотность $\mu$ может быть выражено через пространственную (массовую/объемную) плотность $\rho$ через отношение $\mu =\pi r^{2}\rho =\pi d^{2}\rho /4$, где $r$ - радиус струны и $d$ — это диаметр (он же толщина) в таблице выше:

$f={\frac {1}{2L}}{\sqrt {\frac {T}{\pi d^{2}\rho /4}}}={\frac {1}{2Ld}}{\sqrt {\frac {4T}{\pi \rho }}}={\frac {1}{Ld}}{\sqrt {\frac {T}{\pi \rho }}}$

Для целей вычислений мы можем заменить напряжение $T$ выше, через второй закон Ньютона (сила = масса × ускорение), выражение $T=ma$, где $m$ - это масса, которая на поверхности Земли имела бы эквивалентный вес, соответствующий значениям натяжения $T$ в таблице выше, как связано со стандартным ускорением силы тяжести на поверхности Земли, $g_{0}=980.665$ см/с ² . (Эта замена здесь удобна, поскольку натяжение струн, указанное производителем выше, выражено в фунтах силы , которые удобнее всего преобразовать в эквивалентные массы в килограммах с помощью знакомого коэффициента пересчета 1 фунт = 453,59237 г.) Тогда приведенная выше формула явно выражена. становится:

$f_{\mathrm {Hz} }={\frac {1}{L_{\mathrm {in} }\times 2.54\ \mathrm {cm/in} \times d_{\mathrm {in} }\times 2.54\ \mathrm {cm/in} }}{\sqrt {\frac {T_{\mathrm {lb} }\times 453.59237\ \mathrm {g/lb} \times 980.665\ \mathrm {cm/s^{2}} }{\pi \times \rho _{\mathrm {g/cm^{3}} }}}}$

Используя эту формулу для вычисления $f$ для строки №. 1 выше дает:

$f_{1}={\frac {1}{25.625\ \mathrm {in} \times 2.54\ \mathrm {cm/in} \times 0.00899\ \mathrm {in} \times 2.54\ \mathrm {cm/in} }}{\sqrt {\frac {13.1\ \mathrm {lb} \times 453.59237\ \mathrm {g/lb} \times 980.665\ \mathrm {cm/s^{2}} }{\pi \times 7.726\ \mathrm {g/cm^{3}} }}}\approx 330\ \mathrm {Hz}$

Повторение этого вычисления для всех шести струн приводит к следующим частотам. Рядом с каждой частотой показана музыкальная нота (в научном обозначении высоты тона ) в стандартной настройке гитары, частота которой ближе всего, что подтверждает, что натяжение вышеуказанных струн с рекомендованным производителем натяжением действительно приводит к получению стандартной высоты звука гитары:

Основные гармоники, рассчитанные по приведенным выше формулам вибрации струны.

Номер строки.	Расчетная частота [Гц]	Ближайшая нота в A440 12-TET настройке
1	330	Е 4 (= 440 ÷ 2 5/12 ≈ 329,628 Гц)
2	247	Б 3 (= 440 ÷ 2 10/12 ≈ 246,942 Гц)
3	196	Г 3 (= 440 ÷ 2 14/12 ≈ 195,998 Гц)
4	147	Д 3 (= 440 ÷ 2 19/12 ≈ 146,832 Гц)
5	110	А 2 (= 440 ÷ 2 24/12 = 110 Гц)
6	82.4	Е 2 (= 440 ÷ 2 29/12 ≈ 82,407 Гц)

См. также

• Резные инструменты
• Музыкальная акустика
• Вибрации круглого барабана
• Эксперимент Мелде
• 3-й мост (гармонический резонанс, основанный на равных делениях струн)
• Струнный резонанс
• Изменение фазы отражения

Ссылки

• Молтено, TCA; Н. Б. Туфилларо (сентябрь 2004 г.). «Экспериментальное исследование динамики струны». Американский журнал физики . 72 (9): 1157–1169. Бибкод : 2004AmJPh..72.1157M . дои : 10.1119/1.1764557 .
• Туфилларо, НБ (1989). «Нелинейные и хаотические колебания струны». Американский журнал физики . 57 (5): 408. Бибкод : 1989AmJPh..57..408T . дои : 10.1119/1.16011 .

Специфический

Внешние ссылки

• « Вибрирующая струна » Алена Гориэли и Марка Робертсона-Тесси, Демонстрационный проект Вольфрама .