Функция окна

Термин, используемый в операторах SQL, см. в разделе «Оконная функция (SQL)» .

Популярная оконная функция — окно Ханна . Наиболее популярные оконные функции представляют собой подобные колоколообразные кривые.

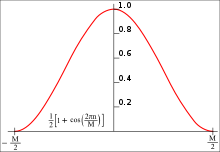
В обработке сигналов и статистике ( используется оконная функция также известная как функция аподизации или функция сужения). ) — математическая функция , имеющая нулевое значение вне некоторого выбранного интервала . Обычно оконные функции симметричны вокруг середины интервала, достигают максимума в середине и сужаются к середине. Математически, когда другая функция или форма сигнала/последовательность данных «умножается» на оконную функцию, произведение также имеет нулевое значение за пределами интервала: остается только часть, где они перекрываются, «вид через окно». Эквивалентно и на практике сегмент данных внутри окна сначала изолируется, а затем только эти данные умножаются на значения оконной функции. Таким образом, основной целью оконных функций является сужение, а не сегментация.

Причины для изучения сегментов более длинной функции включают обнаружение переходных процессов и усреднение по времени частотных спектров. Продолжительность сегментов определяется в каждом приложении такими требованиями, как разрешение по времени и частоте. Но этот метод также изменяет частотный состав сигнала за счет эффекта, называемого утечкой спектра . Оконные функции позволяют нам распределять утечку по спектру различными способами в соответствии с потребностями конкретного приложения. В этой статье подробно описано множество вариантов, но многие различия настолько тонки, что на практике оказываются незначительными.

В типичных приложениях используемые оконные функции представляют собой неотрицательные, плавные, колоколообразные кривые. Также можно использовать прямоугольник, треугольник и другие функции. Более общее определение оконных функций не требует, чтобы они были тождественно равными нулю вне интервала, пока произведение окна, умноженное на его аргумент, интегрируется с квадратом , и, более конкретно, чтобы функция достаточно быстро приближалась к нулю.

Приложения

Оконные функции используются при спектральном анализе /модификации/ ресинтезе , разработка фильтров с конечной импульсной характеристикой , объединяющих многомасштабные и многомерные наборы данных, а также формирование диаграммы направленности и антенны конструкция .

Рисунок 2. Окно синусоиды приводит к утечке спектра. Одинаковая величина утечки происходит независимо от того, присутствует ли в окне целое (синий) или нецелое (красный) количество циклов (строки 1 и 2). Когда синусоида дискретизируется и обрабатывается окном, ее преобразование Фурье с дискретным временем (DTFT) также демонстрирует ту же картину утечки (строки 3 и 4). Но когда DTFT дискретизируется редко, через определенный интервал, можно (в зависимости от вашей точки зрения): (1) избежать утечки или (2) создать иллюзию отсутствия утечки. В случае синего DTFT эти выборки являются выходными данными дискретного преобразования Фурье (ДПФ). Красный DTFT имеет тот же интервал пересечений нуля, но выборки DFT попадают между ними, и обнаруживается утечка.

Спектральный анализ

Основная статья: Спектральная утечка

Преобразование Фурье функции cos( ωt ) равно нулю, за исключением частоты ± ω . Однако многие другие функции и сигналы не имеют удобных преобразований в замкнутой форме. Альтернативно, их спектральный состав может быть интересен только в течение определенного периода времени.

В любом случае преобразование Фурье (или подобное преобразование) может быть применено к одному или нескольким конечным интервалам формы сигнала. Обычно преобразование применяется к произведению формы сигнала и оконной функции. Любое окно (в том числе прямоугольное) влияет на спектральную оценку, вычисляемую этим методом.

Конструкция фильтра

Основная статья: Конструкция фильтра

Окна иногда используются при проектировании цифровых фильтров , в частности, для преобразования «идеальной» импульсной характеристики бесконечной длительности, такой как функция sinc , в конструкцию фильтра с конечной импульсной характеристикой (FIR). Это называется оконным методом .

Статистика и подбор кривой

Основная статья: ядро ​​(статистика)

Оконные функции иногда используются в области статистического анализа, чтобы ограничить набор анализируемых данных диапазоном вблизи заданной точки с весовым коэффициентом , который уменьшает влияние точек, находящихся дальше от подгоняемой части кривой. В области байесовского анализа и подбора кривых его часто называют ядром .

Применение прямоугольных окон

Анализ переходных процессов

При анализе переходного сигнала в модальном анализе , такого как импульс, ударная реакция, синусоидальный импульс, чирп-пакет или шумовой пакет, где распределение энергии по времени крайне неравномерно, прямоугольное окно может быть наиболее подходящим. Например, когда большая часть энергии находится в начале записи, окно непрямоугольной формы ослабляет большую часть энергии, ухудшая соотношение сигнал/шум.

Гармонический анализ

Возможно, кто-то захочет измерить гармонический состав музыкальной ноты определенного инструмента или гармонические искажения усилителя на заданной частоте. Снова обращаясь к рисунку 2 , мы можем заметить, что утечка отсутствует на дискретном наборе гармонически связанных частот, выбранных с помощью дискретного преобразования Фурье (ДПФ). (Спектральные нули на самом деле являются точками пересечения нуля, которые невозможно отобразить в таком логарифмическом масштабе.) Это свойство уникально для прямоугольного окна, и его необходимо соответствующим образом настроить для частоты сигнала, как описано выше.

Перекрывающиеся окна

Когда длина преобразуемого набора данных больше, чем необходимо для обеспечения желаемого разрешения по частоте, общепринятой практикой является разделение его на более мелкие наборы и индивидуальное оконное моделирование. Чтобы уменьшить «потери» по краям окна, отдельные наборы могут перекрываться во времени. См. метод Уэлча степенного спектрального анализа и модифицированное дискретное косинусное преобразование .

Двумерные окна

Основная статья: Двумерный дизайн окна

Двумерные окна обычно используются при обработке изображений для уменьшения нежелательных высоких частот в преобразовании Фурье изображения. Они могут быть построены из одномерных окон в любой из двух форм. Разделяемая форма, $W(m,n)=w(m)w(n)$ вычислить тривиально. Радиальная , форма $W(m,n)=w(r)$, который включает в себя радиус $r={\sqrt {(m-M/2)^{2}+(n-N/2)^{2}}}$, изотропна и не зависит от ориентации осей координат. Только функция Гаусса одновременно сепарабельна и изотропна. Сепарабельные формы всех остальных оконных функций имеют углы, зависящие от выбора осей координат. Изотропия/ анизотропия двумерной оконной функции разделяется ее двумерным преобразованием Фурье. Разница между разделительной и радиальной формами подобна результату дифракции от прямоугольных и круглых отверстий, который можно визуализировать как произведение двух функций sinc и функции Эйри соответственно.

Примеры оконных функций

Соглашения :

• $w_{0}(x)$ — функция нулевой фазы (симметричная относительно $x=0$), непрерывный для $x\in [-N/2,N/2],$ где $N$ целое положительное число (четное или нечетное).
• Последовательность $\{w[n]=w_{0}(n-N/2),\quad 0\leq n\leq N\}$ симметричен длины , $N+1.$
• $\{w[n],\quad 0\leq n\leq N-1\}$ является ДПФ-симметричным , длины $N.$

• Параметр B функции , отображаемый на каждом спектральном графике, представляет собой показатель полосы пропускания, эквивалентный шуму , в единицах интервалов ДПФ .
  • «Спектральная утечка См. разделы « Сигналы дискретного времени» и «Некоторые оконные метрики» и «Нормированная частота» » для понимания использования «элементов» для оси X на этих графиках.

Разреженная выборка дискретного преобразования Фурье (DTFT), такая как DFT на рис. 2, выявляет только утечку в элементы DFT из синусоиды, частота которой также является целочисленным элементом DFT. Невидимые боковые лепестки показывают утечку, которую можно ожидать от синусоид на других частотах. Поэтому при выборе оконной функции обычно важно более плотно сэмплировать DTFT (как мы делаем в этом разделе) и выбирать окно, которое подавляет боковые лепестки до приемлемого уровня.

Прямоугольное окно

Прямоугольное окно

Прямоугольное окно (иногда известное как товарный вагон , или униформа, или Дирихле окно , или ошибочно называемое «без окна» в некоторых программах). ) — это простейшее окно, эквивалентное замене всех кроме N последовательных значений последовательности данных, , нулями, в результате чего сигнал внезапно включается и выключается:

$w[n]=1.$

Другие окна предназначены для смягчения этих внезапных изменений, уменьшения зубчатых потерь и улучшения динамического диапазона (описано в § Спектральный анализ ).

Прямоугольное окно — 1 ^ул. -порядок B -сплайновое окно, а также 0 ^й Окно мощности синуса .

Прямоугольное окно обеспечивает минимальную оценку среднеквадратической ошибки преобразования Фурье дискретного времени за счет других обсуждаемых проблем.

B -сплайновые окна

B -сплайновые окна могут быть получены как k -кратная свертка прямоугольного окна. К ним относятся само прямоугольное окно ( k = 1), § треугольное окно ( k = 2) и § окно Парзена ( k = 4). Альтернативные определения выбирают соответствующие нормализованные B -сплайна базисные функции вместо свертки окон дискретного времени. А к ^й -сплайновая базисная функция -порядка B представляет собой кусочную полиномиальную функцию степени k −1, полученную k -кратной самосверткой прямоугольной функции .

Треугольное окно

Треугольное окно (при L = N + 1)

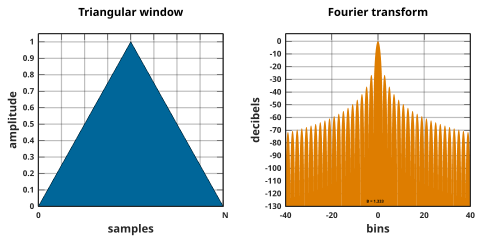
Треугольные окна имеют:

$w[n]=1-\left|{\frac {n-{\frac {N}{2}}}{\frac {L}{2}}}\right|,\quad 0\leq n\leq N$

где L может быть N , Н + 1, или Н +2. Первое из них также известно как Бартлетта окно или Фейера окно . Все три определения сходятся при N. больших

Треугольное окно — это 2 ^nd -порядок B -сплайновое окно. Форму L = N можно рассматривать как свертку двух Прямоугольные окна N / 2 ширины. Преобразование Фурье результата представляет собой квадрат значения преобразования прямоугольного окна половинной ширины.

Окно Парцена

Окно Парцена

Не путать с оценкой плотности ядра .

Определив L ≜ N + 1 , окно Парзена, также известное как окно Валле Пуссена , это 4 ^й -order B -окно сплайна, заданное:

$w_{0}(n)\triangleq \left\{{\begin{array}{ll}1-6\left({\frac {n}{L/2}}\right)^{2}\left(1-{\frac {|n|}{L/2}}\right),&0\leq |n|\leq {\frac {L}{4}}\\2\left(1-{\frac {|n|}{L/2}}\right)^{3}&{\frac {L}{4}}<|n|\leq {\frac {L}{2}}\\\end{array}}\right\}$

$w[n]=\ w_{0}\left(n-{\tfrac {N}{2}}\right),\ 0\leq n\leq N$

окно Уэлча

Другие полиномиальные окна

окно Уэлча

Окно Уэлча состоит из одной параболической секции:

$w[n]=1-\left({\frac {n-{\frac {N}{2}}}{\frac {N}{2}}}\right)^{2},\quad 0\leq n\leq N.$

Определяющий квадратичный полином достигает нулевого значения в выборках сразу за пределами окна.

Синусоидальное окно

Синусоидальное окно

$w[n]=\sin \left({\frac {\pi n}{N}}\right)=\cos \left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.$

Соответствующий $w_{0}(n)\,$ функция представляет собой косинус без смещения фазы π /2. Итак, синусоидальное окно иногда также называют косинусным окном . Поскольку он представляет собой половину цикла синусоидальной функции, его также называют полусинусоидальным окном. или полукосинусное окно .

Автокорреляция . синусоидального окна создает функцию, известную как окно Бомана

Окна мощности синуса/косинуса

Эти оконные функции имеют вид:

$w[n]=\sin ^{\alpha }\left({\frac {\pi n}{N}}\right)=\cos ^{\alpha }\left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.$

Прямоугольное окно ( α = 0 ), синусоидальное окно ( α = 1 ) и окно Ханна ( α = 2 ) являются членами этого семейства.

Для четных значений α эти функции также можно выразить в форме косинусной суммы:

$w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right)-...$

${\begin{array}{l|llll}\hline \alpha &a_{0}&a_{1}&a_{2}&a_{3}&a_{4}\\\hline 0&1\\2&0.5&0.5\\4&0.375&0.5&0.125\\6&0.3125&0.46875&0.1875&0.03125\\8&0.2734375&0.4375&0.21875&0.0625&7.8125\times 10^{-3}\\\hline \end{array}}$

Окна косинусной суммы

Это семейство также известно как обобщенные косинусные окна .

$w[n]=\sum _{k=0}^{K}(-1)^{k}a_{k}\;\cos \left({\frac {2\pi kn}{N}}\right),\quad 0\leq n\leq N.$ ( Уравнение 1 )

В большинстве случаев, включая приведенные ниже примеры, все коэффициенты a _k ≥ 0. Эти окна имеют только 2 K + 1 ненулевой N -точечный коэффициент DFT.

Окна Ханна и Хэмминга

Основная статья: функция Ханна

Он окно

Окно Хэмминга: 0 _{= 0,53836} и 1 _{= 0,46164} . Исходное окно Хэмминга имело бы 0 ₌ = 0,54 и 1 _0,46 .

Обычные окна суммы косинусов для случая K = 1 имеют вид:

$w[n]=a_{0}-\underbrace {(1-a_{0})} _{a_{1}}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad 0\leq n\leq N,$

который легко (и часто) путают с его нулевой версией:

${\begin{aligned}w_{0}(n)\ &=w\left[n+{\tfrac {N}{2}}\right]\\&=a_{0}+a_{1}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad -{\tfrac {N}{2}}\leq n\leq {\tfrac {N}{2}}.\end{aligned}}$

Параметр $a_{0}=0.5$ создает окно Ханна:

$w[n]=0.5\;\left[1-\cos \left({\frac {2\pi n}{N}}\right)\right]=\sin ^{2}\left({\frac {\pi n}{N}}\right),$

назван в честь Юлиуса фон Ханна и иногда ошибочно упоминается как Ханнинг , предположительно из-за его лингвистического и шаблонного сходства с окном Хэмминга. Он также известен как приподнятый косинус , потому что версия с нулевой фазой $w_{0}(n),$ представляет собой одну долю повышенной косинусной функции.

Эта функция является членом семейств косинус-суммы и степени синуса . В отличие от окна Хэмминга , конечные точки окна Ханна просто касаются нуля. В результате боковые лепестки спадают примерно на 18 дБ на октаву.

Параметр $a_{0}$ примерно до 0,54, а точнее 25/46, получается окно Хэмминга , предложенное Ричардом В. Хэммингом . Этот выбор приводит к переходу через нуль на частоте 5 π /( N - 1), что устраняет первый боковой лепесток окна Ханна, придавая ему высоту примерно в одну пятую высоты окна Ханна. Окно Хэмминга часто называют меткой Хэмминга , когда оно используется для формирования импульса .

Приближение коэффициентов до двух десятичных знаков существенно снижает уровень боковых лепестков, почти до состояния равной пульсации. В равновесном смысле оптимальные значения коэффициентов составляют a ₀ = 0,53836 и a ₁ = 0,46164.

Окно Блэкмана

окно Блэкмана; α = 0,16

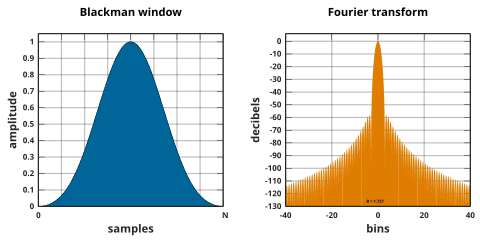
Окна Блэкмана определяются как:

$w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)$

$a_{0}={\frac {1-\alpha }{2}};\quad a_{1}={\frac {1}{2}};\quad a_{2}={\frac {\alpha }{2}}.$

По общему соглашению, неквалифицированный термин « окно Блэкмана » относится к «не очень серьезному предложению» Блэкмана α = 0,16 ( a ₀ = 0,42, a ₁ = 0,5, a ₂ = 0,08), которое близко приближается к точному значению Блэкмана , с 0 _{= 9240/18608 ≈} 0,42659, 1 ₂ 0,49656 и = _{= 7938/18608 ≈} 1430/18608 ≈ 0,076849. Эти точные значения помещают нули в третий и четвертый боковые лепестки. но это приводит к разрыву по краям и спаду на 6 дБ/октаву. Усеченные коэффициенты также не обнуляют боковые лепестки, но имеют улучшенный спад 18 дБ/октаву.

Окно Наттолла, непрерывная первая производная

Окно Наттолла, непрерывная первая производная

Непрерывная форма окна Наттолла, $w_{0}(x),$ и ее первая производная непрерывна всюду, как и функция Ханна . То есть функция обращается к 0 при x = ± N /2, в отличие от окон Блэкмана-Наттолла, Блэкмана-Харриса и Хэмминга. Окно Блэкмана ( α = 0,16 ) также является непрерывным с непрерывной производной на краю, но «точное окно Блэкмана» — нет.

$w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)$

$a_{0}=0.355768;\quad a_{1}=0.487396;\quad a_{2}=0.144232;\quad a_{3}=0.012604.$

Окно Блэкмана – Наттолла

Окно Блэкмана – Наттолла

$w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)$

$a_{0}=0.3635819;\quad a_{1}=0.4891775;\quad a_{2}=0.1365995;\quad a_{3}=0.0106411.$

Окно Блэкмана – Харриса

Окно Блэкмана – Харриса

Обобщение семейства Хэмминга, полученное путем добавления большего количества смещенных функций sinc, предназначенное для минимизации уровней боковых лепестков.

$w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)$

$a_{0}=0.35875;\quad a_{1}=0.48829;\quad a_{2}=0.14128;\quad a_{3}=0.01168.$

Окно с плоской верхушкой

Окно с плоской верхушкой

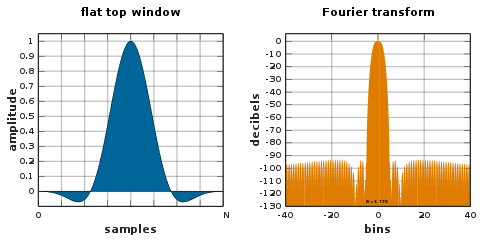
Окно с плоской вершиной — это окно с частичным отрицательным значением, которое имеет минимальные скаллопирующие потери в частотной области. Это свойство желательно для измерения амплитуд синусоидальных частотных составляющих. Однако его широкая полоса пропускания приводит к высокой полосе шума и более широкому выбору частот, что в зависимости от применения может быть недостатком.

Окна с плоским верхом могут быть спроектированы с использованием методов проектирования фильтров нижних частот. или они могут иметь обычную разновидность косинусной суммы :

${\begin{aligned}w[n]=a_{0}&{}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)\\&{}-a_{3}\cos \left({\frac {6\pi n}{N}}\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right).\end{aligned}}$

Вариант Matlab имеет следующие коэффициенты:

$a_{0}=0.21557895;\quad a_{1}=0.41663158;\quad a_{2}=0.277263158;\quad a_{3}=0.083578947;\quad a_{4}=0.006947368.$

Доступны и другие варианты, например, боковые лепестки, которые уменьшаются за счет более высоких значений вблизи главного лепестка.

Окна Райфа – Винсента

Окна Райфа – Винсента обычно масштабируются по среднему значению, равному единице, а не по пиковому значению, равному единице. Значения коэффициентов ниже, примененные к уравнению 1 , отражают этот обычай.

Класс I, порядок 1 ( К = 1): $a_{0}=1;\quad a_{1}=1$ Функционально эквивалентен окну Ханна .

Класс I, порядок 2 ( К = 2): $a_{0}=1;\quad a_{1}={\tfrac {4}{3}};\quad a_{2}={\tfrac {1}{3}}$

Класс I определяется минимизацией амплитуды боковых лепестков высокого порядка. Коэффициенты для заказов до К=4 сведены в таблицу.

Класс II минимизирует ширину главного лепестка при заданном максимальном боковом лепестке.

Класс III представляет собой компромисс, для которого порядок K = 2 напоминает § окно Блэкмана .

Регулируемые окна

Гауссово окно

Гауссово окно, σ = 0,4

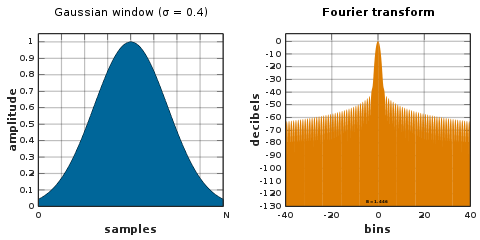
Преобразование Фурье гауссиана также является гауссианом. Поскольку поддержка функции Гаусса распространяется до бесконечности, ее необходимо либо обрезать на концах окна, либо объединить в другое окно с нулевым концом.

Поскольку логарифм гауссовой функции дает параболу , ее можно использовать для почти точной квадратичной интерполяции при оценке частоты .

$w[n]=\exp \left(-{\frac {1}{2}}\left({\frac {n-N/2}{\sigma N/2}}\right)^{2}\right),\quad 0\leq n\leq N.$

$\sigma \leq \;0.5\,$

Стандартное отклонение функции Гаусса составляет σ · N /2 периода выборки.

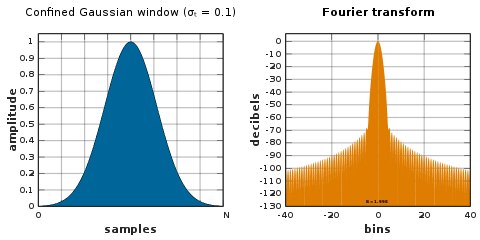
Ограниченное гауссово окно, σ _t = 0,1

Ограниченное гауссово окно

Ограниченное гауссово окно дает наименьшую возможную среднеквадратичную ширину частоты σ _ω для данной временной ширины ( N + 1) σ _t . Эти окна оптимизируют среднеквадратичные значения частотно-временной полосы пропускания. Они вычисляются как минимальные собственные векторы матрицы, зависящей от параметра. Семейство ограниченных гауссовских окон содержит § синусоидальное окно и § гауссово окно в предельных случаях больших и малых σ _t соответственно.

Приблизительное ограниченное гауссово окно, σ _t = 0,1

Приблизительное ограниченное гауссово окно

Определив L ≜ N + 1 , ограниченное гауссово окно временной ширины L × σ _t хорошо аппроксимируется формулой:

$w[n]=G(n)-{\frac {G(-{\tfrac {1}{2}})[G(n+L)+G(n-L)]}{G(-{\tfrac {1}{2}}+L)+G(-{\tfrac {1}{2}}-L)}}$

где $G$ является функцией Гаусса:

$G(x)=\exp \left(-\left({\cfrac {x-{\frac {N}{2}}}{2L\sigma _{t}}}\right)^{2}\right)$

Стандартное отклонение аппроксимированного окна асимптотически равно значения N ) L × σt _{(т.е. большие} для σt _0,14 < .

Обобщенное нормальное окно

Более обобщенная версия гауссова окна — это обобщенное нормальное окно. Сохраняя обозначения гауссовского окна выше, мы можем представить это окно как

$w[n,p]=\exp \left(-\left({\frac {n-N/2}{\sigma N/2}}\right)^{p}\right)$

для любого даже $p$. В $p=2$, это окно Гаусса и так как $p$ подходы $\infty$, это приближается к прямоугольному окну. Преобразование Фурье этого окна не существует в замкнутом виде для общего случая. $p$. Однако он демонстрирует и другие преимущества плавной регулируемой полосы пропускания. Как и окно § Тьюки , это окно, естественно, предлагает «плоскую вершину» для управления затуханием амплитуды временного ряда (в отношении которого у нас нет контроля с помощью окна Гаусса). По сути, он предлагает хороший (контролируемый) компромисс с точки зрения утечки спектра, разрешения по частоте и затухания амплитуды между окном Гаусса и прямоугольным окном.См. также для исследования частотно-временного представления этого окна (или функции).

Окно Тьюки

Окно Тьюки, α = 0,5

Окно Тьюки, также известное как окно с косинусным сужением , можно рассматривать как косинусоидальную долю ширины Nα /2 (охватывающую Nα /2 + 1 наблюдений), которая свернута с прямоугольным окном ширины N (1 − α /2 ) .

$\left.{\begin{array}{lll}w[n]={\frac {1}{2}}\left[1-\cos \left({\frac {2\pi n}{\alpha N}}\right)\right],\quad &0\leq n<{\frac {\alpha N}{2}}\\w[n]=1,\quad &{\frac {\alpha N}{2}}\leq n\leq {\frac {N}{2}}\\w[N-n]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}$

При α = 0 оно становится прямоугольным, а при α = 1 — окном Ханна.

Планковское окно

Окно планковского конуса, ε = 0,25

Так называемое окно «Планковского конуса» представляет собой функцию рельефа , которая широко используется. в теории разбиений единицы в многообразиях . Он гладкий ( $C^{\infty }$ функция) всюду, но равна нулю вне компактной области, ровно единице на интервале внутри этой области и плавно и монотонно меняется между этими пределами. Его использование в качестве оконной функции при обработке сигналов было впервые предложено в контексте гравитационно-волновой астрономии , вдохновленной распределением Планка . Она определяется как кусочная функция :

$\left.{\begin{array}{lll}w[0]=0,\\w[n]=\left(1+\exp \left({\frac {\varepsilon N}{n}}-{\frac {\varepsilon N}{\varepsilon N-n}}\right)\right)^{-1},\quad &1\leq n<\varepsilon N\\w[n]=1,\quad &\varepsilon N\leq n\leq {\frac {N}{2}}\\w[N-n]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}$

Величина сужения контролируется параметром ε : меньшие значения дают более резкие переходы.

DPSS или окно Слепиана

DPSS (дискретная вытянутая сфероидальная последовательность) или окно Слепия максимизирует концентрацию энергии в главном лепестке . и используется в многоконусном спектральном анализе, который усредняет шум в спектре и уменьшает потери информации по краям окна.

Главный лепесток заканчивается в интервале частоты, заданном параметром α .

Окно DPSS, α = 2

Окно DPSS, α = 3

Окна Кайзера, представленные ниже, созданы путем простой аппроксимации окон DPSS:

Окно Кайзера, α = 2

Окно Кайзера, α = 3

Окно Кайзера

Основная статья: Окно Кайзера

Окно Кайзера, или Кайзера-Бесселя, представляет собой простую аппроксимацию окна DPSS с использованием функций Бесселя , открытого Джеймсом Кайзером .

$w[n]={\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2n}{N}}-1\right)^{2}}}\right)}{I_{0}(\pi \alpha )}},\quad 0\leq n\leq N$

$w_{0}(n)={\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2n}{N}}\right)^{2}}}\right)}{I_{0}(\pi \alpha )}},\quad -N/2\leq n\leq N/2$

где $I_{0}$ это 0 ^й -порядковая модифицированная функция Бесселя первого рода. Переменный параметр $\alpha$ определяет компромисс между шириной основного лепестка и уровнями боковых лепестков диаграммы спектральной утечки. Ширина основного лепестка между нулями определяется выражением $2{\sqrt {1+\alpha ^{2}}},$ в единицах бункеров DFT, и типичное значение $\alpha$ это 3.

Окно Дольфа – Чебышева

Окно Дольфа – Чебышева, α = 5

Минимизирует чебышевскую норму боковых лепестков для заданной ширины основного лепестка.

Нулевая фазовая оконная функция Дольфа – Чебышева $w_{0}[n]$ обычно определяется через вещественное дискретное преобразование Фурье , $W_{0}[k]$:

$W_{0}(k)={\frac {T_{N}{\big (}\beta \cos \left({\frac {\pi k}{N+1}}\right){\big )}}{T_{N}(\beta )}}={\frac {T_{N}{\big (}\beta \cos \left({\frac {\pi k}{N+1}}\right){\big )}}{10^{\alpha }}},\ 0\leq k\leq N.$

T _n ( x ) — n -й полином Чебышева первого рода, оцененный по x , который можно вычислить с помощью

$T_{n}(x)={\begin{cases}\cos \!{\big (}n\cos ^{-1}(x){\big )}&{\text{if }}-1\leq x\leq 1\\\cosh \!{\big (}n\cosh ^{-1}(x){\big )}&{\text{if }}x\geq 1\\(-1)^{n}\cosh \!{\big (}n\cosh ^{-1}(-x){\big )}&{\text{if }}x\leq -1,\end{cases}}$

и

$\beta =\cosh \!{\big (}{\tfrac {1}{N}}\cosh ^{-1}(10^{\alpha }){\big )}$

это уникальное положительное реальное решение $T_{N}(\beta )=10^{\alpha }$, где параметр α устанавливает чебышевскую норму боковых лепестков, равную −20 α децибел.

Оконную функцию можно вычислить по W ₀ ( k ) с помощью обратного дискретного преобразования Фурье (ДПФ):

$w_{0}(n)={\frac {1}{N+1}}\sum _{k=0}^{N}W_{0}(k)\cdot e^{i2\pi kn/(N+1)},\ -N/2\leq n\leq N/2.$

Лагированную версию окна можно получить следующим образом:

$w[n]=w_{0}\left(n-{\frac {N}{2}}\right),\quad 0\leq n\leq N,$

который для четных значений N необходимо вычислять следующим образом:

${\begin{aligned}w_{0}\left(n-{\frac {N}{2}}\right)={\frac {1}{N+1}}\sum _{k=0}^{N}W_{0}(k)\cdot e^{\frac {i2\pi k(n-N/2)}{N+1}}={\frac {1}{N+1}}\sum _{k=0}^{N}\left[\left(-e^{\frac {i\pi }{N+1}}\right)^{k}\cdot W_{0}(k)\right]e^{\frac {i2\pi kn}{N+1}},\end{aligned}}$

что является обратным ДПФ $\left(-e^{\frac {i\pi }{N+1}}\right)^{k}\cdot W_{0}(k).$

Вариации:

• Из-за условия равной пульсации окно временной области имеет разрывы по краям. Приближение, позволяющее избежать их, позволяя равномерным рябьм спадать по краям, — это окно Тейлора .
• Также доступна альтернатива определению обратного ДПФ. [1] .

Ультрасферическое окно

ультрасферического окна Параметр μ определяет, уменьшаются ли амплитуды боковых лепестков преобразования Фурье, остаются на одном уровне или (показано здесь) увеличиваются с частотой.

Ультрасферическое окно было предложено Роем Стрейтом в 1984 году. и имеет применение в конструкции антенных решеток, нерекурсивный дизайн фильтра, и спектральный анализ.

Как и другие настраиваемые окна, ультрасферическое окно имеет параметры, которые можно использовать для управления шириной основного лепестка преобразования Фурье и относительной амплитудой боковых лепестков. В отличие от других окон, оно имеет дополнительный параметр, который можно использовать для установки скорости уменьшения (или увеличения) амплитуды боковых лепестков.

Окно можно выразить во временной области следующим образом:

$w[n]={\frac {1}{N+1}}\left[C_{N}^{\mu }(x_{0})+\sum _{k=1}^{\frac {N}{2}}C_{N}^{\mu }\left(x_{0}\cos {\frac {k\pi }{N+1}}\right)\cos {\frac {2n\pi k}{N+1}}\right]$

где $C_{N}^{\mu }$ – ультрасферический полином степени N, а $x_{0}$ и $\mu$ контролировать диаграмму направленности боковых лепестков.

Определенные конкретные значения $\mu$ выведите другие известные окна: $\mu =0$ и $\mu =1$ дайте окна Дольфа – Чебышева и Сарамяки соответственно. См. здесь иллюстрацию ультрасферических окон с различной параметризацией.

Экспоненциальное окно или окно Пуассона

Экспоненциальное окно, τ = N /2

Экспоненциальное окно, τ = ( N /2)/(60/8,69)

Окно Пуассона, или, в более общем смысле, экспоненциальное окно, экспоненциально увеличивается к центру окна и экспоненциально уменьшается во второй половине. Поскольку показательная функция никогда не достигает нуля, значения окна в ее пределах не равны нулю (это можно рассматривать как умножение показательной функции на прямоугольное окно). ). Это определяется

$w[n]=e^{-\left|n-{\frac {N}{2}}\right|{\frac {1}{\tau }}},$

где τ — постоянная времени функции. Экспоненциальная функция затухает как e ≃ 2,71828 или примерно 8,69 дБ на постоянную времени. Это означает, что для целевого затухания D дБ на половине длины окна постоянная времени τ определяется выражением

$\tau ={\frac {N}{2}}{\frac {8.69}{D}}.$

Гибридные окна

Оконные функции также создавались как мультипликативные или аддитивные комбинации других окон.

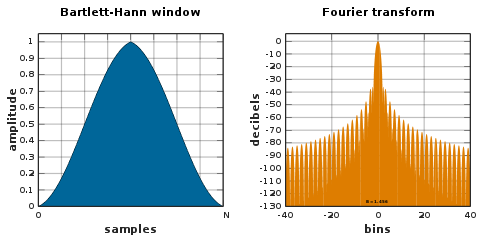
Окно Бартлетта – Ханна

Окно Бартлетта – Ханна

$w[n]=a_{0}-a_{1}\left|{\frac {n}{N}}-{\frac {1}{2}}\right|-a_{2}\cos \left({\frac {2\pi n}{N}}\right)$

$a_{0}=0.62;\quad a_{1}=0.48;\quad a_{2}=0.38\,$

Окно Планка – Бесселя

Окно Планка–Бесселя, ε = 0,1, α = 4,45

§ Окно конуса Планка, умноженное на окно Кайзера , которое определяется в терминах модифицированной функции Бесселя . Эта гибридная оконная функция была введена для уменьшения пикового уровня боковых лепестков окна сужения Планка, сохраняя при этом его хорошее асимптотическое затухание. Он имеет два настраиваемых параметра: ε из конуса Планка и α из окна Кайзера, поэтому его можно настроить в соответствии с требованиями данного сигнала.

Окно Ханна – Пуассона

Окно Ханна – Пуассона, α = 2

Окно Ханна, умноженное на окно Пуассона . Для $\alpha \geqslant 2$ у него нет боковых лепестков, поскольку его преобразование Фурье навсегда спадает за пределами главного лепестка без локальных минимумов. Таким образом, его можно использовать в восхождения на холм алгоритмах , таких как метод Ньютона . Окно Ханна-Пуассона определяется:

$w[n]={\frac {1}{2}}\left(1-\cos \left({\frac {2\pi n}{N}}\right)\right)e^{\frac {-\alpha \left|N-2n\right|}{N}}\,$

где α — параметр, контролирующий наклон экспоненты.

Другие окна

Окно GAP (окно Наттолла, оптимизированное для GAP)

Окно обобщенного адаптивного полинома (GAP)

Окно GAP — это семейство настраиваемых оконных функций, основанных на симметричном полиномиальном разложении порядка. $K$. Оно непрерывно с непрерывной производной всюду. При соответствующем наборе коэффициентов разложения и порядке разложения окно GAP может имитировать все известные оконные функции, точно воспроизводя их спектральные свойства.

$w_{0}[n]=a_{0}+\sum _{k=1}^{K}a_{2k}\left({\frac {n}{\sigma }}\right)^{2k},\quad -{\frac {N}{2}}\leq n\leq {\frac {N}{2}},$

где $\sigma$ является стандартным отклонением $\{n\}$ последовательность.

Кроме того, начиная с набора коэффициентов расширения $a_{2k}$ которое имитирует определенную известную оконную функцию, окно GAP можно оптимизировать с помощью процедур минимизации, чтобы получить новый набор коэффициентов, которые улучшают одно или несколько спектральных свойств, таких как ширина основного лепестка, затухание боковых лепестков и скорость спада боковых лепестков. Таким образом, можно разработать оконную функцию GAP с заданными спектральными свойствами в зависимости от конкретного приложения.

Окно Синка или Ланцоша

Окно Ланчош

$$w[n]=\operatorname {sinc} \left({\frac {2n}{N}}-1\right)$$

• используется при повторной выборке Ланцоша
• для окна Ланцоша, $\operatorname {sinc} (x)$ определяется как $\sin(\pi x)/\pi x$
• также известное как окно sinc , потому что: $$w_{0}(n)=\operatorname {sinc} \left({\frac {2n}{N}}\right)\,$$ является основным лепестком нормализованной функции sinc

Асимметричные оконные функции

The $w_{0}(x)$ форма, согласно приведенному выше соглашению, симметрична вокруг $x=0$. Однако существуют оконные функции, которые являются асимметричными, например, распределение гаммы, используемое в КИХ-реализациях фильтров Gammatone . Эти асимметрии используются для уменьшения задержки при использовании больших размеров окна или для подчеркивания начального переходного процесса затухающего импульса.

В качестве оконной функции можно легко использовать любую ограниченную функцию с компактным носителем , в том числе асимметричную. Кроме того, существуют способы преобразования симметричных окон в асимметричные путем преобразования временной координаты, например, с помощью приведенной ниже формулы.

$x\leftarrow N\left({\frac {x}{N}}+{\frac {1}{2}}\right)^{\alpha }-{\frac {N}{2}}\,,$

где окно имеет больший вес для самых ранних образцов, когда $\alpha >1$и, наоборот, придает больший вес последним образцам, когда $\alpha <1$.

См. также

• Аподизация
• Фильтр Колмогорова – Зурбенко
• Мультиконусность
• Кратковременное преобразование Фурье
• Спектральная утечка
• метод Уэлча
• Весовая функция
• Метод оформления окна

Дальнейшее чтение

• Харрис, Фредерик Дж. (сентябрь 1976 г.). «Окна, гармонический анализ и дискретное преобразование Фурье» (PDF) . apps.dtic.mil . Подводный военно-морской центр, Сан-Диего. Архивировано (PDF) из оригинала 8 апреля 2019 г. Проверено 08 апреля 2019 г.
• Альбрехт, Ганс Хельге (2012). Настроенные окна суммы косинусов с минимальным боковым лепестком и минимальным боковым лепестком. Версия 1.0 . Том ISBN 978-3-86918-281-0). редактор: Физико-технический федеральный институт. Физико-технический федеральный институт. дои : 10.7795/110.20121022aa . ISBN  978-3-86918-281-0 .
• Берген, ЮВА; Антониу, А. (2005). «Проектирование нерекурсивных цифровых фильтров с использованием функции ультрасферического окна» . Журнал EURASIP по прикладной обработке сигналов . 2005 (12): 1910–1922. Бибкод : 2005EJASP2005...44B . дои : 10.1155/ASP.2005.1910 .
• Прабху, КММ (2014). Оконные функции и их применение в обработке сигналов . Бока-Ратон, Флорида: CRC Press. ISBN  978-1-4665-1583-3 .
• Патент США 7065150 , Пак, Ён-Со, «Система и способ генерации модуляции корневого косинусного мультиплексирования с ортогональным частотным разделением (RRC OFDM)», опубликован в 2003 г., выдан в 2006 г.  

Внешние ссылки

• СМИ, связанные с функцией окна, на Викискладе?
• Справка LabView, Характеристики сглаживающих фильтров, http://zone.ni.com/reference/en-XX/help/371361B-01/lvanlsconcepts/char_smoothing_windows/
• Создание и свойства оконных функций косинусной суммы, http://electronicsart.weebly.com/fftwindows.html
• Онлайн-интерактивное БПФ, моделирование Windows, разрешения и утечек | РИТЭК | Библиотека и инструменты