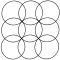
Сетка перекрывающихся кругов

Пример перекрывающихся круглых фигур
квадратная круговая сетка
1+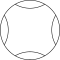
4
9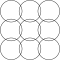
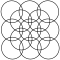
Центрированные квадратные решетчатые формы
5
13

треугольная круговая сетка
1+
3
4
7
19

Сетка перекрывающихся кругов представляет собой геометрический узор из повторяющихся перекрывающихся кругов одинакового радиуса в двумерном пространстве . Обычно дизайн основан на кругах с центрами на треугольниках (с простой формой из двух кругов, называемой vesica piscis ) или на квадратной решетке из точек.

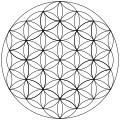
Узоры из семи перекрывающихся кругов появляются на исторических артефактах, начиная с VII века до нашей эры; они стали часто используемым орнаментом в период Римской империи и сохранились в средневековых художественных традициях как в исламском искусстве ( гирих украшения ), так и в готическом искусстве . Название «Цветок Жизни» дано узору перекрывающихся кругов в публикациях Нью Эйдж .

Особый интерес представляет шестилепестковая розетка, созданная на основе узора «семь перекрывающихся кругов», также известного как « Солнце Альп » из-за его частого использования в альпийском народном искусстве 17 и 18 веков.

Треугольная сетка перекрывающихся кругов

Треугольная форма решетки с радиусами кругов, равными их разделению, называется сеткой из семи перекрывающихся кругов . ^[1] Он содержит 6 кругов, пересекающихся в одной точке, с центром в этом пересечении седьмой круг.

нечасто использовались в различных декоративных искусствах Перекрывающиеся круги со схожими геометрическими конструкциями с древних времен . Этот узор нашел широкое применение в массовой культуре, моде , ювелирных изделиях , татуировках и декоративных изделиях.

Культурное значение

Ближний Восток

Самое старое известное появление рисунка «перекрывающихся кругов» датируется VII или VI веком до нашей эры. найден на пороге дворца ассирийского царя Ашшур-бани-апли в Дур Шаррукине (ныне находится в Лувре ). ^[2]

Этот дизайн становится более распространенным в первые века нашей эры. Одним из первых примеров являются пять узоров из 19 перекрывающихся кругов, нарисованных на гранитных колоннах храма Осириса в Абидосе , Египет . ^[3] и еще пять на колонне напротив здания. Они нарисованы красной охрой , некоторые из них очень тусклые и их трудно различить. ^[4] Узоры представляют собой граффити и не встречаются в исконно египетских орнаментах. В основном они датируются первыми веками христианской эры. ^[5] хотя средневековое или даже современное (начало 20 века) происхождение нельзя с уверенностью исключать, поскольку рисунки не упоминаются в обширных списках граффити в храме, составленных Маргарет Мюррей в 1904 году. ^[6]

Подобные узоры иногда использовались в Англии в качестве апотропных знаков, не позволяющих ведьмам проникать в здания. ^[7] Кресты освящения, обозначающие точки в храмах, помазанные святой водой во время освящения храмов, также имеют форму перекрывающихся кругов.

Узор гирих , который можно нарисовать с помощью циркуля и линейки.

Оконная клетка во дворце Топкапы с использованием узора

В исламском искусстве узор представляет собой одно из нескольких расположений кругов (другие используются для четырех- или пятикратных рисунков), используемых для построения сеток для исламских геометрических узоров . Он используется для создания узоров с 6- и 12-конечными звездами, а также шестиугольниками в стиле гирих . Однако полученные узоры характерно скрывают строительную сетку, представляя вместо этого дизайн переплетенных ремешков . ^[8]

Европа

Узоры из семи перекрывающихся кругов встречаются на римских мозаиках, например, во дворце Ирода в I веке до нашей эры. ^[9]

Рисунок находится на одной из серебряных пластинок позднеримского клада Кайзераугст (обнаружен в 1961 году). ^[10] Позже он встречается как орнамент в готической архитектуре , а еще позже — в европейском народном искусстве раннего Нового времени.

Примеры высокого средневековья включают тротуары Космати в Вестминстерском аббатстве (13 век). ^[11] Леонардо да Винчи подробно обсудил математические пропорции конструкции. ^[12]

Современное использование

Название «Цветок жизни» современное, связано с движением Нью Эйдж и обычно приписывается Друнвало Мелхиседеку в его книге «Древняя тайна цветка жизни» (1999). ^[13]^[14]

Узор и современное название получили широкое распространение в массовой культуре, моде, ювелирных изделиях, татуировках и декоративных изделиях. Узор в выстегивании назвали бриллиантовым обручальным кольцом или треугольным обручальным кольцом, чтобы отличать его от квадратного узора . Помимо периодического использования в моде, ^[15] он также используется в декоративном искусстве. Например, в альбоме Sempiternal (2013) группы Bring Me the Horizon используется сетка из 61 перекрывающегося круга . в качестве основной особенности обложки альбома ^[16] тогда как в альбоме A Head Full of Dreams (2015) группы Coldplay сетка из 19 перекрывающихся кругов является центральной частью обложки альбома. Плакаты-тизеры, иллюстрирующие обложку книги « Голова, полная мечтаний» , были широко развешаны в лондонском метро в последнюю неделю октября 2015 года. ^[17]

Символ «Солнце Альп» ( итальянский Sole delle Alpi ) использовался в качестве эмблемы паданского национализма на севере Италии с 1990-х годов. ^[18] Это напоминает узор, часто встречающийся в этом районе на зданиях. ^[19]

Семикруговой «Цветок Жизни» также используется на гербе Асгардии космической державы .

Галерея

Шестиугольный вариант с 1, 7 и 19 кругами

В примерах ниже узор имеет шестиугольный контур и дополнительно очерчен.

Рисунок Леонардо да Винчи из Атлантического кодекса , между 1478 и 1519 годами.
Рисунок Леонардо да Винчи ( Атлантический кодекс , л. 307v)
1-круг с завершенными дугами
7-круг: Мозаичный пол бани во дворце Ирода , I век до н.э.
Символ из 19 кругов с завершенными дугами, ограниченный большим кругом.
19-круг: два символа, нарисованные красной охрой. Храм Осириса в Абидосе, Египет.
19-круг: Окно на южной апсиде церкви монастыря Превели (Moni Preveli), Крит.
19-круг: Из Эфеса , Турция.

Подобные шаблоны

В примерах ниже узор не имеет шестиугольного контура.

Чаша с мифологическими сценами, фризом со сфинксом и изображением короля, побеждающего своих врагов. Кипро-архаика I (VIII–VII вв. до н.э.). Из Идалиона, Кипр .
Мяч, который держит мужчина-императорский лев-хранитель у Врат Высшей Гармонии , Запретный город , Пекин , Китай, демонстрирует геометрический узор на его поверхности.
Украшение пола дворца короля Ашшурбанипала на севере Ирака , которое можно увидеть в Лувре, датированное 645 годом до нашей эры.
Кофейная чашка (Германия, 2022 г.)
Эмблема « Солнце Альп », используемая Лигой Севера.

Строительство

Марта Бартфельд, автор учебников по геометрическому искусству, описала свое независимое открытие этого дизайна в 1968 году. В ее первоначальном определении говорилось: «Этот дизайн состоит из кругов радиусом 1 [дюйм; 25 мм], каждая точка пересечения которых служит новый центр. Дизайн можно расширять до бесконечности в зависимости от того, сколько раз отмечены нечетные точки».

Фигуру узора можно нарисовать ручкой и циркулем , создав несколько серий взаимосвязанных кругов одинакового диаметра, соприкасающихся с центром предыдущего круга. Второй круг центрируется в любой точке первого круга. Все последующие круги центрированы на пересечении двух других кругов.

Прогрессии

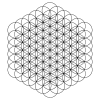
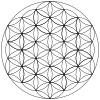
Узор можно расширить наружу в виде концентрических шестиугольных колец из кругов, как показано на рисунке. В первом ряду показаны кольца кругов. Во второй строке показана трехмерная интерпретация набора кубов сфер размером n × n × n , если смотреть с диагональной оси. В третьей строке показан узор, завершенный частичными дугами окружностей внутри набора завершенных кругов.

Расширяющиеся множества имеют 1, 7, 19, 37, 61, 91, 127 и т. д. кругов, а также продолжающиеся все большие шестиугольные кольца кругов. Количество кругов равно n. ³-( п -1) ³ = 3н ²-3 n +1 = 3 n ( n -1)+1.

Эти перекрывающиеся круги также можно рассматривать как проекцию n -единичного куба сфер в трехмерном пространстве, если смотреть на диагональную ось. Сфер больше, чем кругов, потому что некоторые из них перекрываются в двух измерениях.

Фигуры- розетки , включая неполные круги
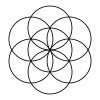
1-круг	7-круг (8-1)	19-круг (27-8)	37-круг (64-27)	61-круг (125-64)	91-круг (216-125)	127-круг... (343-216)

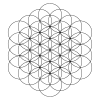
1-сфера (1×1×1)	8-сфера (2×2×2)	27-сфера (3×3×3)	64-сфера (4×4×4)	125-сфера (5×5×5)	216-сфера (6×6×6)	343-сфера (7×7×7)
			(изображение отсутствует)	(изображение отсутствует)	(изображение отсутствует)	(изображение отсутствует)
+12 дуг	+24 дуги	+36 дуг	+48 дуг	+60 дуг	+72 дуги	+84 дуги

Другие варианты

еще одна треугольная форма решетки Распространена , в которой расстояние между кругами равно квадратному корню из трехкратного их радиуса. Ричард Кершнер показал в 1939 году, что никакое расположение кругов не может покрыть плоскость более эффективно, чем расположение шестиугольной решетки. ^[20]

Две смещенные копии этого кругового узора образуют ромбический узор мозаики , а три копии образуют исходный треугольный узор.

пример 19 кругов
Две смещенные копии минимального узора покрывающего круга (слева) образуют узор ромбической плитки , как в этой красно-синей версии.
Три смещенные копии минимального узора закрывающих кругов (крайнее левое изображение) образуют узор из 7 кругов, как в этой красной, зеленой и синей версии.
Пример керамической глазурованной банки Айюбидов Ракки . Сирия, 12/13 века.
Черно-белый мозаичный пол на вилле Адриана , Тиволи, II век нашей эры.

Связанные понятия

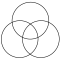
Центральная линза фигуры из двух кругов называется vesica piscis от Евклида . Две окружности также называются окружностями Вильярсо как плоское пересечение тора. Области внутри одного круга и за пределами другого круга называются луной .

Фигура из трех кругов напоминает изображение колец Борромео и используется в трех множеств теории диаграммах Венна . Его внутренняя часть образует уникурсальный путь, называемый трикетрой . Центр фигуры из трех кругов называется треугольником Рело .

Рыба-пузырь	Борромео кольца	Диаграмма друзей	Три раза	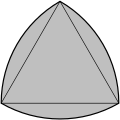Треугольник Рело

Некоторые сферические многогранники с ребрами вдоль больших кругов можно стереографически спроецировать на плоскость как перекрывающиеся круги.

Многогранники в стереографической проекции
Октаэдр	Кубооктаэдр	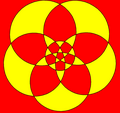Икосододекаэдр

Узор из семи кругов также называют исламским узором из семи кругов из- за его использования в исламском искусстве .

Квадратная сетка перекрывающихся кругов

Квадратная форма решетки
Радиус круга равен квадратному корню, умноженному на 2 их расстояния (расстояния между их центрами).	называется Лоскутное одеяло рисунком двойного обручального кольца.

Центрированная квадратная решётка
Его можно рассматривать как две полусмещенные квадратные сетки из касательных кругов.	Египетский дизайн из книги Оуэна Джонса «Грамматика орнамента» (1856 г.)

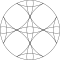
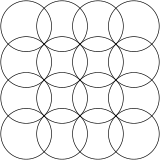
Квадратную форму решетки можно увидеть в виде кругов, которые выстраиваются горизонтально и вертикально, пересекаясь по диагонали. Узор выглядит немного иначе, если его повернуть по диагонали, что также называется формой центрированной квадратной решетки , поскольку его можно рассматривать как две квадратные решетки, каждая из которых сосредоточена в промежутках другой.

он называется мотивом Кавунг В индонезийском батике и встречается на стенах индуистского храма Прамбанан 8-го века на Яве .

математике он называется Апсамиккум В древнем месопотамском . ^[21]

Квадратную сетку можно увидеть в виде гранецентрированной кубической решетки с 12 сферами, соприкасающимися вокруг каждой сферы.
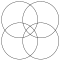
Соответствующая сетка из пяти перекрывающихся кругов строится из двух наборов перекрывающихся кругов с половинным смещением. ^[22]
Кавунг или из батика саронг «Кофейные зерна» (фрагмент), Ява, Индонезия.

См. также

Теория узлов
Мутации симметрии равномерного тайлинга - мутации узоров в трехмерном пространстве.

Ссылки

^ Исламское искусство и геометрический дизайн: деятельность для обучения
^ Лувр, инв.-№. АО 19915 . Жорж Перро, Шарль Чипьез, История искусства в Халдее и Ассирии , том. 1, Лондон, 1884 г., стр. 240, (gutenberg.org)
^ Вайсштейн, Эрик В. «Цветок жизни» . Математический мир .
^ Стюарт, Малкольм (2008). «Цветок Жизни» и Осирион – Факты интереснее Фантазий» . Египетский тур (Дэвид Ферлонг) . Проверено 8 ноября 2015 г.
^ Ферлонг, Дэвид. «Осирион и цветок жизни» . Проверено 8 ноября 2015 г. Ферлонг утверждает, что эти гравюры могут быть датированы не ранее 535 г. до н.э. и, вероятно, датируются 2-м и 4-м веками нашей эры. Его исследование основано на фотографических свидетельствах греческого текста, которые еще предстоит полностью расшифровать. Текст виден рядом с рисунками и в верхней части колонн высотой более 4 метров. Ферлонг предполагает, что Осирион был наполовину заполнен песком до того, как были нарисованы круги, и, следовательно, вероятно, это произошло намного позже конца династии Птолемеев .
^ Мюррей, Маргарет Элис (1904). Осирион в Абидосе, Лондон . п. 35 . Проверено 4 ноября 2015 г.
^ Кеннеди, Маев (31 октября 2016 г.). "Ведьмины метки: общественность попросили найти древние царапины на зданиях" . Хранитель . Проверено 31 октября 2016 г.
^ Бруг, Эрик (2008). Исламские геометрические узоры . Темза и Гудзон . стр. 22–23 и пассим. ISBN 978-0-500-28721-7 .
^ Кац, Юджин А.; Джин, Би-Яу (август 2016 г.). Хайлебрук, Дирк (ред.). «Фуллерены, многогранники и китайские львы-хранители». Математический турист. Математический интеллект . 38 (3): 61–68. дои : 10.1007/s00283-016-9663-0 .
^ Ганс Ульрих Инстинский: Находка позднеримского серебра из Кайзераугста. Майнц 1971 г., мемориальная доска 85.
^ Тротуары Космати в Вестминстерском аббатстве. Проверено 14 сентября 2013 г.
^ Атлантический кодекс , след. 307р–309в, 459р (1478–1519 гг.).
^ Бартфельд, Марта (2005). Как создавать мандалы сакральной геометрии . Санта-Фе, Нью-Мексико: Mandalart Creations. п. 35. ISBN 9780966228526 . OCLC 70293628 .
^ Вайсштейн, Эрик В. (12 декабря 2002 г.). CRC Краткая математическая энциклопедия, второе издание . CRC Press (опубликовано в 2002 г.). п. 1079. ИСБН 1420035223 .
^ Например Заман, Сана (14 мая 2013 г.). «Заим Джамал представляет новую коллекцию на борту частной яхты в Дубай Марина» . Высокая жизнь . Проверено 9 ноября 2015 г.
^ Купер, Эд (25 февраля 2013 г.). «Bring Me The Horizon: Этот альбом должен длиться вечно» . Независимый . Архивировано из оригинала 23 октября 2015 года . Проверено 8 ноября 2015 г.
^ Денхэм, Джесс (6 ноября 2015 г.). «Новый альбом Coldplay: Бейонсе и Ноэль Галлахер выступят в программе A Head Full of Dreams» . Независимый . Архивировано из оригинала 24 мая 2022 г. Проверено 8 ноября 2015 г.
^ «Значение символа Солнца Альп» (на итальянском языке). Северная лига. Архивировано из оригинала 12 января 2014 года . Проверено 1 декабря 2014 г.
^ Ивано Дорболо (6 июня 2010 г.). «Церковь С.Эджидио и символ Солнца Альп» . История границ – долины Натисоне . Проверено 9 ноября 2015 г.
^ Сферические упаковки, решетки и группы , Джон Конвей, Нил Дж. А. Слоан, Глава 2, раздел 1.1, Покрытие пространства перекрывающимся кругом. стр. 31-32. Рисунок 2.1. Покрытие плоскости кругами (б) Более эффективное или более тонкое покрытие в гексагональной решетке. [1]
^ Месопотамская математика 2100–1600 до н. э.: Технические константы в бюрократии и образовании (Оксфордские издания клинописных текстов), Элеонора Робсон, Clarendon Press, 1999, ISBN 978-0198152460 [2] на books.google.com.
^ Создание квадратных сеток из кругов

Внешние ссылки

[1] Исламское искусство и геометрический дизайн: деятельность для обучения

[2] Лувр, инв.-№. АО 19915 . Жорж Перро, Шарль Чипьез, История искусства в Халдее и Ассирии , том. 1, Лондон, 1884 г., стр. 240, (gutenberg.org)

[3] Вайсштейн, Эрик В. «Цветок жизни» . Математический мир .

[furlong2-4] Стюарт, Малкольм (2008). «Цветок Жизни» и Осирион – Факты интереснее Фантазий» . Египетский тур (Дэвид Ферлонг) . Проверено 8 ноября 2015 г.

[furlong1-5] Ферлонг, Дэвид. «Осирион и цветок жизни» . Проверено 8 ноября 2015 г. Ферлонг утверждает, что эти гравюры могут быть датированы не ранее 535 г. до н.э. и, вероятно, датируются 2-м и 4-м веками нашей эры. Его исследование основано на фотографических свидетельствах греческого текста, которые еще предстоит полностью расшифровать. Текст виден рядом с рисунками и в верхней части колонн высотой более 4 метров. Ферлонг предполагает, что Осирион был наполовину заполнен песком до того, как были нарисованы круги, и, следовательно, вероятно, это произошло намного позже конца династии Птолемеев .

[murray-6] Мюррей, Маргарет Элис (1904). Осирион в Абидосе, Лондон . п. 35 . Проверено 4 ноября 2015 г.

[Kennedy2016-7] Кеннеди, Маев (31 октября 2016 г.). "Ведьмины метки: общественность попросили найти древние царапины на зданиях" . Хранитель . Проверено 31 октября 2016 г.

[8] Бруг, Эрик (2008). Исламские геометрические узоры . Темза и Гудзон . стр. 22–23 и пассим. ISBN 978-0-500-28721-7 .

[9] Кац, Юджин А.; Джин, Би-Яу (август 2016 г.). Хайлебрук, Дирк (ред.). «Фуллерены, многогранники и китайские львы-хранители». Математический турист. Математический интеллект . 38 (3): 61–68. дои : 10.1007/s00283-016-9663-0 .

[10] Ганс Ульрих Инстинский: Находка позднеримского серебра из Кайзераугста. Майнц 1971 г., мемориальная доска 85.

[11] Тротуары Космати в Вестминстерском аббатстве. Проверено 14 сентября 2013 г.

[12] Атлантический кодекс , след. 307р–309в, 459р (1478–1519 гг.).

[HTCSGM-13] Бартфельд, Марта (2005). Как создавать мандалы сакральной геометрии . Санта-Фе, Нью-Мексико: Mandalart Creations. п. 35. ISBN 9780966228526 . OCLC 70293628 .

[14] Вайсштейн, Эрик В. (12 декабря 2002 г.). CRC Краткая математическая энциклопедия, второе издание . CRC Press (опубликовано в 2002 г.). п. 1079. ИСБН 1420035223 .

[15] Например Заман, Сана (14 мая 2013 г.). «Заим Джамал представляет новую коллекцию на борту частной яхты в Дубай Марина» . Высокая жизнь . Проверено 9 ноября 2015 г.

[16] Купер, Эд (25 февраля 2013 г.). «Bring Me The Horizon: Этот альбом должен длиться вечно» . Независимый . Архивировано из оригинала 23 октября 2015 года . Проверено 8 ноября 2015 г.

[17] Денхэм, Джесс (6 ноября 2015 г.). «Новый альбом Coldplay: Бейонсе и Ноэль Галлахер выступят в программе A Head Full of Dreams» . Независимый . Архивировано из оригинала 24 мая 2022 г. Проверено 8 ноября 2015 г.

[18] «Значение символа Солнца Альп» (на итальянском языке). Северная лига. Архивировано из оригинала 12 января 2014 года . Проверено 1 декабря 2014 г.

[19] Ивано Дорболо (6 июня 2010 г.). «Церковь С.Эджидио и символ Солнца Альп» . История границ – долины Натисоне . Проверено 9 ноября 2015 г.

[20] Сферические упаковки, решетки и группы , Джон Конвей, Нил Дж. А. Слоан, Глава 2, раздел 1.1, Покрытие пространства перекрывающимся кругом. стр. 31-32. Рисунок 2.1. Покрытие плоскости кругами (б) Более эффективное или более тонкое покрытие в гексагональной решетке. [1]

[21] Месопотамская математика 2100–1600 до н. э.: Технические константы в бюрократии и образовании (Оксфордские издания клинописных текстов), Элеонора Робсон, Clarendon Press, 1999, ISBN 978-0198152460 [2] на books.google.com.

[22] Создание квадратных сеток из кругов

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]