✖


Jump to content

Мутации симметрии равномерного тайлинга

Add links
Пример * n 32 мутации симметрии
Сферические мозаики ( n = 3..5)

*332
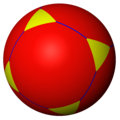*432
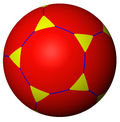*532
Замощение евклидовой плоскости ( n = 6)

*632
Гиперболические плоские мозаики ( n = 7...∞)

*732
*832
... *∞32

В геометрии мутация симметрии — это отображение фундаментальных областей между двумя группами симметрии. [ 1 ] Они компактно выражаются в орбифолдной записи . Эти мутации могут происходить от сферических мозаик к евклидовым и гиперболическим мозаикам . Гиперболические мозаики также можно разделить на компактные, паракомпактные и расходящиеся случаи.

Однородные мозаики — это простейшее применение этих мутаций, хотя в фундаментальной области можно выразить и более сложные закономерности.

В этой статье представлены прогрессивные последовательности однородных мозаик внутри семейств симметрии.

Мутации орбифолдов

[ редактировать ]

Орбифолды с одинаковой структурой могут мутировать между разными классами симметрии, в том числе в областях кривизны от сферической до евклидовой и гиперболической. В этой таблице показаны классы мутаций. [ 1 ] Эта таблица не является полной для возможных гиперболических орбифолдов.

Орбифолд сферический евклидов гиперболический
тот - тот -
пп 22, 33 ... ∞∞ -
*пп *22, *33 ... *∞∞ -
п* 2*, 3* ... ∞* -
p× 2×, 3× ... ∞×
** - ** -
*× - *× -
×× - ×× -
ппп 222 333 444 ...
пп* - 22* 33* ...
pp× - 22× 33×, 44× ...
сеть 222, 322 ... , 233 244 255 ..., 433 ...
пкр 234, 235 236 237 ..., 245 ...
пк* - - 23*, 24* ...
pq× - - 23×, 24× ...
п*к 2*2, 2*3 ... 3*3, 4*2 5*2 5*3 ..., 4*3, 4*4 ..., 3*4, 3*5 ...
*п* - - *2* ...
*p× - - *2× ...
пппп - 2222 3333 ...
pppq - - 2223...
ппкк - - 2233
пп*п - - 22*2 ...
п*qr - 2*22 3*22 ..., 2*32 ...
*ппп *222 *333 *444 ...
*pqq *стр22, *233 *244 *255 ..., *344...
*pqr *234, *235 *236 *237..., *245..., *345 ...
п*ппп - - 2*222
*pqrs - *2222 *2223...
*пппппп - - *22222 ...
...

* n 22 симметрия

[ редактировать ]

Регулярные мозаики

[ редактировать ]
Семейство правильных осоэдров · * n 22 мутации симметрии правильных осоэдров: nn
Космос сферический евклидов
Укладка плитки
имя 		шестиугольный
осоэдр 		Дигональный
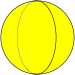
осоэдр 		Треугольный
осоэдр 		Квадрат
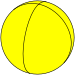
осоэдр 		пятиугольный
осоэдр 		... Апейрогональный
осоэдр
Укладка плитки
изображение 		...
Шлефли
символ 		{2,1} {2,2} {2,3} {2,4} {2,5} ... {2,∞}
Коксетер
диаграмма 		...
Лица и
края 		1 2 3 4 5 ... ∞
Вершины 2 2 2 2 2 ... 2
Вертекс
конфиг. 		2 2.2 2 3 2 4 2 5 ... 2 ∞
Семейство правильных двугранников · * n 22 мутации симметрии правильных двугранных мозаик: nn
Космос сферический евклидов
Укладка плитки
имя 		моногональный
двугранник 		Дигональный
двугранник 		Треугольный
двугранник 		Квадрат
двугранник 		пятиугольный
двугранник 		... Апейрогональный
двугранник
Укладка плитки
изображение 		...
Шлефли
символ 		{1,2} {2,2} {3,2} {4,2} {5,2} ... {∞,2}
Коксетер
диаграмма 		...
Лица 2 {1} 2 {2} 2 {3} 2 {4} 2 {5} ... 2 {∞}
Края и
вершины 		1 2 3 4 5 ... ∞
Вертекс
конфиг. 		1.1 2.2 3.3 4.4 5.5 ... ∞.∞

Разбиение призм

[ редактировать ]
* n 22 мутации симметрии однородных призм : n .4.4
Космос сферический евклидов
Укладка плитки
Конфиг. 3.4.4 4.4.4 5.4.4 6.4.4 7.4.4 8.4.4 9.4.4 10.4.4 11.4.4 12.4.4 ... ∞.4.4

Антипризматические мозаики

[ редактировать ]
* n 22 мутации симметрии разбиений антипризм: V n .3.3.3
Космос сферический евклидов
Укладка плитки
Конфиг. 2.3.3.3 3.3.3.3 4.3.3.3 5.3.3.3 6.3.3.3 7.3.3.3 8.3.3.3 ... ∞.3.3.3

* n 32 симметрия

[ редактировать ]

Регулярные мозаики

[ редактировать ]
* n 32 мутация симметрии правильных мозаик: {3, n }
Spherical Euclid. Compact hyper. Paraco. Noncompact hyperbolic
3.3 33 34 35 36 37 38 3∞ 312i 39i 36i 33i
* n 32 мутация симметрии правильных мозаик: { n ,3}
Spherical Euclidean Compact hyperb. Paraco. Noncompact hyperbolic
{2,3} {3,3} {4,3} {5,3} {6,3} {7,3} {8,3} {∞,3} {12i,3} {9i,3} {6i,3} {3i,3}

Усеченные мозаики

[ редактировать ]
* n 32 мутация симметрии усеченных мозаик: t{ n ,3}
Symmetry
*n32
[n,3] 		Spherical Euclid. Compact hyperb. Paraco. Noncompact hyperbolic
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3]... 		*∞32
[∞,3] 		[12i,3] [9i,3] [6i,3]
Truncated
figures
Symbol t{2,3} t{3,3} t{4,3} t{5,3} t{6,3} t{7,3} t{8,3} t{∞,3} t{12i,3} t{9i,3} t{6i,3}
Triakis
figures
Config. V3.4.4 V3.6.6 V3.8.8 V3.10.10 V3.12.12 V3.14.14 V3.16.16 V3.∞.∞
* n 32 мутация симметрии усеченных мозаик: n .6.6
Sym.
*n42
[n,3] 		Spherical Euclid. Compact Parac. Noncompact hyperbolic
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3]... 		*∞32
[∞,3] 		[12i,3] [9i,3] [6i,3]
Truncated
figures
Config. 2.6.6 3.6.6 4.6.6 5.6.6 6.6.6 7.6.6 8.6.6 ∞.6.6 12i.6.6 9i.6.6 6i.6.6
n-kis
figures
Config. V2.6.6 V3.6.6 V4.6.6 V5.6.6 V6.6.6 V7.6.6 V8.6.6 V∞.6.6 V12i.6.6 V9i.6.6 V6i.6.6

Квазирегулярные мозаики

[ редактировать ]
Квазирегулярные разбиения: (3.n) 2
Sym.
*n32
[n,3] 		Spherical Euclid. Compact hyperb. Paraco. Noncompact hyperbolic
*332
[3,3]
Td 		*432
[4,3]
Oh 		*532
[5,3]
Ih 		*632
[6,3]
p6m 		*732
[7,3]
  		*832
[8,3]...
  		*∞32
[∞,3]
  		[12i,3] [9i,3] [6i,3]
Figure
Figure
Vertex (3.3)2 (3.4)2 (3.5)2 (3.6)2 (3.7)2 (3.8)2 (3.∞)2 (3.12i)2 (3.9i)2 (3.6i)2
Schläfli r{3,3} r{3,4} r{3,5} r{3,6} r{3,7} r{3,8} r{3,∞} r{3,12i} r{3,9i} r{3,6i}
Coxeter
Dual uniform figures
Dual
conf.
V(3.3)2
V(3.4)2
V(3.5)2
V(3.6)2
V(3.7)2
V(3.8)2
V(3.∞)2
Мутации симметрии двойственных квазирегулярных мозаик: V(3.n) 2
*n32 Spherical Euclidean Hyperbolic
*332 *432 *532 *632 *732 *832... *∞32
Tiling
Conf. V(3.3)2 V(3.4)2 V(3.5)2 V(3.6)2 V(3.7)2 V(3.8)2 V(3.∞)2

Расширенные мозаики

[ редактировать ]
* n 32 мутация симметрии развернутых мозаик: 3.4. № .4
Symmetry
*n32
[n,3] 		Spherical Euclid. Compact hyperb. Paraco. Noncompact hyperbolic
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3]... 		*∞32
[∞,3] 		 
[12i,3] 		 
[9i,3] 		 
[6i,3]
Figure
Config. 3.4.2.4 3.4.3.4 3.4.4.4 3.4.5.4 3.4.6.4 3.4.7.4 3.4.8.4 3.4.∞.4 3.4.12i.4 3.4.9i.4 3.4.6i.4
* n 32 мутация симметрии двойных расширенных мозаик: V3.4. № .4
Симметрия
* № 32
[н,3] 		сферический Евклид. Компактный гиперб. Парако.
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3]... 		*∞32
[∞,3]
Фигура
Конфиг.
Версия 3.4.2.4
Версия 3.4.3.4
Версия 3.4.4.4
Версия 3.4.5.4
Версия 3.4.6.4
Версия 3.4.7.4
Версия 3.4.8.4
V3.4.∞.4

Всеусеченные мозаики

[ редактировать ]
* n 32 мутация симметрии всеусеченных мозаик: 4.6.2n
Sym.
*n32
[n,3] 		Spherical Euclid. Compact hyperb. Paraco. Noncompact hyperbolic
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3] 		*∞32
[∞,3] 		 
[12i,3] 		 
[9i,3] 		 
[6i,3] 		 
[3i,3]
Figures
Config. 4.6.4 4.6.6 4.6.8 4.6.10 4.6.12 4.6.14 4.6.16 4.6.∞ 4.6.24i 4.6.18i 4.6.12i 4.6.6i
Duals
Config. V4.6.4 V4.6.6 V4.6.8 V4.6.10 V4.6.12 V4.6.14 V4.6.16 V4.6.∞ V4.6.24i V4.6.18i V4.6.12i V4.6.6i

Курносые плитки

[ редактировать ]
n 32 мутации симметрии курносых мозаик: 3.3.3.3.n
Symmetry
n32 		Spherical Euclidean Compact hyperbolic Paracomp.
232 332 432 532 632 732 832 ∞32
Snub
figures
Config. 3.3.3.3.2 3.3.3.3.3 3.3.3.3.4 3.3.3.3.5 3.3.3.3.6 3.3.3.3.7 3.3.3.3.8 3.3.3.3.∞
Gyro
figures
Config. V3.3.3.3.2 V3.3.3.3.3 V3.3.3.3.4 V3.3.3.3.5 V3.3.3.3.6 V3.3.3.3.7 V3.3.3.3.8 V3.3.3.3.∞

* n 42 симметрия

[ редактировать ]

Регулярные мозаики

[ редактировать ]
* n 42 мутация симметрии правильных мозаик: {4, n }
Spherical Euclidean Compact hyperbolic Paracompact

{4,3}
{4,4}
{4,5}
{4,6}
{4,7}
{4,8}...
{4,∞}
* n 42 мутация симметрии регулярных мозаик: { n ,4}
Spherical Euclidean Hyperbolic tilings
24 34 44 54 64 74 84 ...∞4

Квазирегулярные мозаики

[ редактировать ]
* n 42 мутации симметрии квазирегулярных мозаик: (4. n ) 2
Symmetry
*4n2
[n,4] 		Spherical Euclidean Compact hyperbolic Paracompact Noncompact
*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4]... 		*∞42
[∞,4] 		 
[ni,4]
Figures
Config. (4.3)2 (4.4)2 (4.5)2 (4.6)2 (4.7)2 (4.8)2 (4.∞)2 (4.ni)2
* n 42 мутации симметрии квазирегулярных двойственных мозаик: V (4.n) 2
Symmetry
*4n2
[n,4] 		Spherical Euclidean Compact hyperbolic Paracompact Noncompact
*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4]... 		*∞42
[∞,4] 		 
[iπ/λ,4]
Tiling
 
Conf.
V4.3.4.3
V4.4.4.4
V4.5.4.5
V4.6.4.6
V4.7.4.7
V4.8.4.8
V4.∞.4.∞ 		V4.∞.4.∞

Усеченные мозаики

[ редактировать ]
* n 42 мутация симметрии усеченных мозаик: 4,2 n .2 n
Symmetry
*n42
[n,4] 		Spherical Euclidean Compact hyperbolic Paracomp.
*242
[2,4] 		*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4]... 		*∞42
[∞,4]
Truncated
figures
Config. 4.4.4 4.6.6 4.8.8 4.10.10 4.12.12 4.14.14 4.16.16 4.∞.∞
n-kis
figures
Config. V4.4.4 V4.6.6 V4.8.8 V4.10.10 V4.12.12 V4.14.14 V4.16.16 V4.∞.∞
* n 42 мутация симметрии усеченных мозаик: n.8.8
Symmetry
*n42
[n,4] 		Spherical Euclidean Compact hyperbolic Paracompact
*242
[2,4] 		*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4]... 		*∞42
[∞,4]
Truncated
figures
Config. 2.8.8 3.8.8 4.8.8 5.8.8 6.8.8 7.8.8 8.8.8 ∞.8.8
n-kis
figures
Config. V2.8.8 V3.8.8 V4.8.8 V5.8.8 V6.8.8 V7.8.8 V8.8.8 V∞.8.8

Расширенные мозаики

[ редактировать ]
* n 42 мутация симметрии расширенных мозаик: n .4.4.4
Symmetry
[n,4], (*n42) 		Spherical Euclidean Compact hyperbolic Paracomp.
*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4] 		*∞42
[∞,4]
Expanded
figures
Config. 3.4.4.4 4.4.4.4 5.4.4.4 6.4.4.4 7.4.4.4 8.4.4.4 ∞.4.4.4
Rhombic
figures
config.
V3.4.4.4
V4.4.4.4
V5.4.4.4
V6.4.4.4
V7.4.4.4
V8.4.4.4
V∞.4.4.4

Всеусеченные мозаики

[ редактировать ]
* n 42 мутация симметрии всеусеченных мозаик: 4.8.2n
Symmetry
*n42
[n,4] 		Spherical Euclidean Compact hyperbolic Paracomp.
*242
[2,4] 		*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4]... 		*∞42
[∞,4]
Omnitruncated
figure
4.8.4
4.8.6
4.8.8
4.8.10
4.8.12
4.8.14
4.8.16
4.8.∞
Omnitruncated
duals
V4.8.4
V4.8.6
V4.8.8
V4.8.10
V4.8.12
V4.8.14
V4.8.16
V4.8.∞

Курносые плитки

[ редактировать ]
4 n 2 мутации симметрии курносых мозаик: 3.3.4.3.n
Symmetry
4n2 		Spherical Euclidean Compact hyperbolic Paracomp.
242 342 442 542 642 742 842 ∞42
Snub
figures
Config. 3.3.4.3.2 3.3.4.3.3 3.3.4.3.4 3.3.4.3.5 3.3.4.3.6 3.3.4.3.7 3.3.4.3.8 3.3.4.3.∞
Gyro
figures
Config. V3.3.4.3.2 V3.3.4.3.3 V3.3.4.3.4 V3.3.4.3.5 V3.3.4.3.6 V3.3.4.3.7 V3.3.4.3.8 V3.3.4.3.∞

* n 52 симметрия

[ редактировать ]

Регулярные мозаики

[ редактировать ]
* n 52 мутация симметрии усеченных мозаик: 5 н
Сфера Гиперболическая плоскость

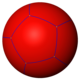{5,3}
{5,4}
{5,5}
{5,6}
{5,7}
{5,8}
... {5,∞}

* n 62 симметрия

[ редактировать ]

Регулярные мозаики

[ редактировать ]
* n 62 мутация симметрии правильных мозаик: {6, n }
Spherical Euclidean Hyperbolic tilings

{6,2}
{6,3}
{6,4}
{6,5}
{6,6}
{6,7}
{6,8} 		...
{6,∞}

* n 82 симметрия

[ редактировать ]

Регулярные мозаики

[ редактировать ]
n 82 мутации симметрии правильных мозаик: 8 н
Космос сферический Компактный гиперболический Паракомпакт
Укладка плитки
Конфиг. 8.8 8 3 8 4 8 5 8 6 8 7 8 8 ... 8 ∞

Ссылки

[ редактировать ]
  1. ^ Jump up to: а б Мутации двумерной симметрии Дэниел Хьюсон

Источники

[ редактировать ]
  • Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN   978-1-56881-220-5 [1]
  • От гиперболического 2-мерного пространства к евклидову 3-мерному пространству: мозаика и шаблоны через топологию Стивен Хайд
Retrieved from "https://en.wikipedia.org/w/index.php?title=Uniform_tiling_symmetry_mutations&oldid=1189601855"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: a6092ead1895a92cc3e52f0d9f134a80__1702407360
URL1:https://arc.ask3.ru/arc/aa/a6/80/a6092ead1895a92cc3e52f0d9f134a80.html
Заголовок, (Title) документа по адресу, URL1:
Uniform tiling symmetry mutations - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)