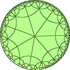
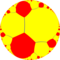
Symmetric subdivision in hyperbolic geometry
Примеры однородных мозаик сферический евклидов гиперболический {5,3} {6,3} {7,3} {∞,3} Регулярные мозаики т{5,3} т{6,3} т{7,3} т{∞,3} Усеченные мозаики имеют 2p.2p.q фигур вершин из обычного {p,q}. г{5,3} г{6,3} г{7,3} Квазирегулярные мозаики рр{5,3} рр{6,3} рр{7,3} рр{∞,3} Полуправильные мозаики тр{5,3} тр{6,3} тр{7,3} тр{∞,3} Всеусеченные мозаики
Построение архимедовых тел и мозаик показывать Симметрия Треугольная двугранная симметрия Тетраэдрический Октаэдрический икосаэдрический p6m симметрия [3,7] симметрия [3,8] симметрия Starting solid Symbol Triangular hosohedron Triangular dihedron Tetrahedron Cube Octahedron Dodecahedron Icosahedron Hexagonal tiling Triangular tiling Heptagonal tiling Order-7 triangular tiling Octagonal tiling Order-8 triangular tiling Truncation (t)t{p,q} triangular prism truncated triangular dihedron (Half of the "edges" count as degenerate digon faces . The other half are normal edges.) truncated tetrahedron truncated cube truncated octahedron truncated dodecahedron truncated icosahedron Truncated hexagonal tiling Truncated triangular tiling Truncated heptagonal tiling Truncated order-7 triangular tiling Truncated octagonal tiling Truncated order-8 triangular tiling Rectification (r)r{p,q} tridihedron (All of the "edges" count as degenerate digon faces .) tetratetrahedron cuboctahedron icosidodecahedron Trihexagonal tiling Triheptagonal tiling Trioctagonal tiling Bitruncation (2t)2t{p,q} truncated triangular dihedron(Half of the "edges" count as degenerate digon faces . The other half are normal edges.) triangular prism truncated tetrahedron truncated octahedron truncated cube truncated icosahedron truncated dodecahedron truncated triangular tiling truncated hexagonal tiling Truncated order-7 triangular tiling Truncated heptagonal tiling Truncated order-8 triangular tiling Truncated octagonal tiling Birectification (2r)Dual (d)2r{p,q} triangular dihedron triangular hosohedron tetrahedron octahedron cube icosahedron dodecahedron triangular tiling hexagonal tiling Order-7 triangular tiling Heptagonal tiling Order-8 triangular tiling Octagonal tiling Cantellation (rr)Expansion (e)rr{p,q} triangular prism (The "edge" between each pair of tetragons counts as a degenerate digon face . The other edges (the ones between a trigon and a tetragon) are normal edges.) rhombitetratetrahedron rhombicuboctahedron rhombicosidodecahedron rhombitrihexagonal tiling Rhombitriheptagonal tiling Rhombitrioctagonal tiling Snub rectified (sr)Snub (s) sr{p,q} triangular antiprism (Three yellow-yellow "edges", no two of which share any vertices, count as degenerate digon faces . The other edges are normal edges.) snub tetratetrahedron snub cuboctahedron snub icosidodecahedron snub trihexagonal tiling Snub triheptagonal tiling Snub trioctagonal tiling Cantitruncation (tr)tr{p,q} hexagonal prism truncated tetratetrahedron truncated cuboctahedron truncated icosidodecahedron truncated trihexagonal tiling Truncated triheptagonal tiling Truncated trioctagonal tiling
В гиперболической геометрии равномерное гиперболическое замощение (или регулярное, квазирегулярное или полуправильное гиперболическое замощение) представляет собой заполнение гиперболической плоскости от края до края, которое имеет правильные многоугольники в качестве граней и является вершинно-транзитивным ( транзитивным на своих вершинах , изогональным, т.е. существует изометрия , отображающая любую вершину на любую другую). Отсюда следует, что все вершины конгруэнтны , а мозаика имеет высокую степень вращательной и трансляционной симметрии .
Однородные мозаики можно идентифицировать по конфигурации их вершин — последовательности чисел, представляющей количество сторон многоугольников вокруг каждой вершины. Например, 7.7.7 представляет собой семиугольную мозаику , в каждой вершине которой находится по 3 семиугольника . Он также является правильным, поскольку все многоугольники имеют одинаковый размер, поэтому ему также можно присвоить символ Шлефли {7,3}.
Однородные мозаики могут быть регулярными (если также транзитивны по граням и граням), квазирегулярными (если транзитивны по граням, но не по граням) или полуправильными (если не транзитивны ни по граням, ни по граням). Для прямоугольных треугольников ( p q 2) существует две правильные мозаики, представленные символами Шлефли { p , q } и { q , p }.
Пример конструкции Витхоффа с прямоугольными треугольниками ( r = 2) и 7 образующими точками. Линии, ведущие к активным зеркалам, окрашены в красный, желтый и синий цвета, а три узла напротив них связаны с символом Витхоффа. Существует бесконечное количество однородных мозаик, основанных на треугольниках Шварца ( p q r ), где 1 / p + 1 / q + 1 / r < 1, где p , q , r — каждый порядок симметрии отражения в трёх точках треугольника фундаментальной области — группа симметрии представляет собой группу гиперболического треугольника .
Каждое семейство симметрии содержит 7 однородных мозаик, определяемых символом Витхоффа или диаграммой Кокстера-Динкина , 7 из которых представляют собой комбинации из 3 активных зеркал. Восьмая представляет собой операцию чередования , удаляющую альтернативные вершины из высшей формы со всеми активными зеркалами.
Семейства с r = 2 содержат регулярные гиперболические мозаики , определенные группой Кокстера , такой как [7,3], [8,3], [9,3], ... [5,4], [6,4], ....
Гиперболические семейства с r = 3 или выше определяются как ( p q r ) и включают (4 3 3), (5 3 3), (6 3 3) ... (4 4 3), (5 4 3), ... (4 4 4)....
Гиперболические треугольники ( p q r ) определяют компактные однородные гиперболические мозаики. В пределе любой из p , q или r может быть заменен на ∞, который определяет паракомпактный гиперболический треугольник и создает равномерные мозаики либо с бесконечными гранями (называемыми апейрогонами ), которые сходятся к одной идеальной точке, либо с бесконечной вершинной фигурой с бесконечным количеством расходящихся ребер. из той же идеальной точки.
Больше семейств симметрии можно построить из фундаментальных областей, не являющихся треугольниками.
Ниже показаны избранные семейства однородных мозаик (с использованием модели диска Пуанкаре для гиперболической плоскости). Три из них – (7 3 2), (5 4 2) и (4 3 3) – и никакие другие не являются минимальными в том смысле, что если любое из их определяющих чисел заменить меньшим целым числом, результирующий шаблон будет либо Евклидова или сферическая, а не гиперболическая; и наоборот, любое из чисел можно увеличить (даже до бесконечности), чтобы создать другие гиперболические шаблоны.
Каждая равномерная мозаика порождает двойную равномерную мозаику , многие из которых также приведены ниже.
Существует бесконечно много ( p q 2) семейств групп треугольников . В этой статье показаны регулярные замощения до p , q = 8 и равномерные замощения в 12 семействах: (7 3 2), (8 3 2), (5 4 2), (6 4 2), (7 4 2). , (8 4 2), (5 5 2), (6 5 2) (6 6 2), (7 7 2), (8 6 2) и (8 8 2).
Простейшим набором гиперболических мозаик являются правильные мозаики { p , q }, которые существуют в матрице с правильными многогранниками и евклидовыми мозаиками. Обычное замощение { p , q } имеет двойственное замощение { q , p } по диагональной оси таблицы. Самодвойственные мозаики {2,2}, {3,3} , {4,4} , {5,5} и т. д. проходят по диагонали таблицы.
показывать Spherical (improper /Platonic) /Euclidean /hyperbolic (Poincaré disc: compact /paracompact /noncompact ) tessellations with their Schläfli symbol p \ q 2 3 4 5 6 7 8 ... ∞ ... iπ/λ 2 {2 ,2} {2,3} {2,4} {2,5} {2,6} {2,7} {2,8} {2,∞} 3 {3,2} tetrahedron )octahedron )icosahedron )deltille ){3,7} {3,8} {3,∞} 4 {4,2} cube )quadrille ){4,5} {4,6} {4,7} {4,8} {4,∞} 5 {5,2} dodecahedron ){5,4} {5,5} {5,6} {5,7} {5,8} {5,∞} 6 {6,2} hextille ){6,4} {6,5} {6,6} {6,7} {6,8} {6,∞} 7 {7,2} {7,3} {7,4} {7,5} {7,6} {7,7} {7,8} {7,∞} {7,iπ/λ} 8 {8,2} {8,3} {8,4} {8,5} {8,6} {8,7} {8,8} {8,∞} {8,iπ/λ} ... ∞ {∞,2} {∞,3} {∞,4} {∞,5} {∞,6} {∞,7} {∞,8} {∞,∞} ... iπ/λ {iπ/λ,7} {iπ/λ,8} {iπ/λ, iπ/λ}
Группа (7 3 2) треугольников , группа Кокстера [7,3], орбифолд (*732) содержит эти равномерные мозаики:
показывать Однородные семиугольные/треугольные мозаики Symmetry: [7,3], (*732) [7,3]+ , (732) {7,3} t{7,3} r{7,3} t{3,7} {3,7} rr{7,3} tr{7,3} sr{7,3} Uniform duals V73 V3.14.14 V3.7.3.7 V6.6.7 V37 V3.4.7.4 V4.6.14 V3.3.3.3.7
Группа (8 3 2) треугольников , группа Кокстера [8,3], орбифолд (*832) содержит эти равномерные мозаики:
показывать Symmetry: [8,3], (*832) [8,3]+ [1+ ,8,3] [8,3+ ] {8,3} t{8,3} r{8,3} t{3,8} {3,8} rr{8,3} 2 {3,8}tr{8,3} sr{8,3} h{8,3} h2 {8,3} s{3,8} Uniform duals V83 V3.16.16 V3.8.3.8 V6.6.8 V38 V3.4.8.4 V4.6.16 V34 .8 V(3.4)3 V8.6.6 V35 .4
Группа (5 4 2) треугольников , группа Кокстера [5,4], орбифолд (*542) содержит эти равномерные мозаики:
показывать Однородные пятиугольные/квадратные плитки Symmetry: [5,4], (*542) [5,4]+ , (542) [5+ ,4], (5*2) [5,4,1+ ], (*552) {5,4} t{5,4} r{5,4} 2t{5,4}=t{4,5} 2r{5,4}={4,5} rr{5,4} tr{5,4} sr{5,4} s{5,4} h{4,5} Uniform duals V54 V4.10.10 V4.5.4.5 V5.8.8 V45 V4.4.5.4 V4.8.10 V3.3.4.3.5 V3.3.5.3.5 V55
Группа (6 4 2) треугольников , группа Кокстера [6,4], орбифолд (*642) содержит эти равномерные разбиения. Поскольку все элементы четные, каждый из них представляет собой фундаментальную область отражательной симметрии: *3333, *662, *3232, *443, *222222, *3222 и *642 соответственно. Кроме того, все 7 однородных плиток можно чередовать, и у них также есть двойные.
показывать Однородные тетрагексагональные мозаики Symmetry : [6,4], (*642 ){6,4} t{6,4} r{6,4} t{4,6} {4,6} rr{6,4} tr{6,4} Uniform duals V64 V4.12.12 V(4.6)2 V6.8.8 V46 V4.4.4.6 V4.8.12 Alternations [1+ ,6,4] [6+ ,4] [6,1+ ,4] [6,4+ ] [6,4,1+ ] [(6,4,2+ )] [6,4]+ h{6,4} s{6,4} hr{6,4} s{4,6} h{4,6} hrr{6,4} sr{6,4}
Группа (7 4 2) треугольников , группа Кокстера [7,4], орбифолд (*742) содержит эти равномерные мозаики:
показывать Однородные семиугольные/квадратные мозаики Symmetry: [7,4], (*742) [7,4]+ , (742) [7+ ,4], (7*2) [7,4,1+ ], (*772) {7,4} t{7,4} r{7,4} 2t{7,4}=t{4,7} 2r{7,4}={4,7} rr{7,4} tr{7,4} sr{7,4} s{7,4} h{4,7} Uniform duals V74 V4.14.14 V4.7.4.7 V7.8.8 V47 V4.4.7.4 V4.8.14 V3.3.4.3.7 V3.3.7.3.7 V77
Группа (8 4 2) треугольников , группа Кокстера [8,4], орбифолд (*842) содержит эти равномерные разбиения. Поскольку все элементы четные, каждый из них представляет собой фундаментальную область отражательной симметрии: *4444, *882, *4242, *444, *22222222, *4222 и *842 соответственно. Кроме того, все 7 однородных плиток можно чередовать, и у них также есть двойные.
показывать Однородные восьмиугольные/квадратные плитки [8,4], (*842) {8,4} t{8,4} r{8,4} 2t{8,4}=t{4,8} 2r{8,4}={4,8} rr{8,4} tr{8,4} Uniform duals V84 V4.16.16 V(4.8)2 V8.8.8 V48 V4.4.4.8 V4.8.16 Alternations [1+ ,8,4] [8+ ,4] [8,1+ ,4] [8,4+ ] [8,4,1+ ] [(8,4,2+ )] [8,4]+ h{8,4} s{8,4} hr{8,4} s{4,8} h{4,8} hrr{8,4} sr{8,4} Alternation duals V(4.4)4 V3.(3.8)2 V(4.4.4)2 V(3.4)3 V88 V4.44 V3.3.4.3.8
Группа (5 5 2) треугольников , группа Кокстера [5,5], орбифолд (*552) содержит эти равномерные мозаики:
показывать Однородные пятипентагональные мозаики Symmetry: [5,5], (*552) [5,5]+ , (552) Order-5 pentagonal tiling {5,5} Truncated order-5 pentagonal tiling t{5,5} Order-4 pentagonal tiling r{5,5} Truncated order-5 pentagonal tiling 2t{5,5} = t{5,5} Order-5 pentagonal tiling 2r{5,5} = {5,5} Tetrapentagonal tiling rr{5,5} Truncated order-4 pentagonal tiling tr{5,5} Snub pentapentagonal tiling sr{5,5} Uniform duals Order-5 pentagonal tiling V5.5.5.5.5 V5.10.10 Order-5 square tiling V5.5.5.5 V5.10.10 Order-5 pentagonal tiling V5.5.5.5.5 V4.5.4.5 V4.10.10 V3.3.5.3.5
Группа (6 5 2) треугольников , группа Кокстера [6,5], орбифолд (*652) содержит эти равномерные мозаики:
показывать Symmetry: [6,5], (*652) [6,5]+ , (652) [6,5+ ], (5*3) [1+ ,6,5], (*553) {6,5} t{6,5} r{6,5} 2t{6,5}=t{5,6} 2r{6,5}={5,6} rr{6,5} tr{6,5} sr{6,5} s{5,6} h{6,5} Uniform duals V65 V5.12.12 V5.6.5.6 V6.10.10 V56 V4.5.4.6 V4.10.12 V3.3.5.3.6 V3.3.3.5.3.5 V(3.5)5
Группа (6 6 2) треугольников , группа Кокстера [6,6], орбифолд (*662) содержит эти равномерные мозаики:
показывать Равномерные шестиугольные мозаики Symmetry: [6,6], (*662) {6,6} t{6,6} 2 {4,6}r{6,6} t{6,6} 2 {4,6}{6,6} rr{6,6} tr{6,6} Uniform duals V66 V6.12.12 V6.6.6.6 V6.12.12 V66 V4.6.4.6 V4.12.12 Alternations [1+ ,6,6] [6+ ,6] [6,1+ ,6] [6,6+ ] [6,6,1+ ] [(6,6,2+ )] [6,6]+ h{6,6} s{6,6} hr{6,6} s{6,6} h{6,6} hrr{6,6} sr{6,6}
Группа (8 6 2) треугольников , группа Кокстера [8,6], орбифолд (*862) содержит эти равномерные разбиения.
показывать Однородные восьмиугольные/шестиугольные плитки Symmetry : [8,6], (*862) {8,6} t{8,6} r{8,6} 2t{8,6}=t{6,8} 2r{8,6}={6,8} rr{8,6} tr{8,6} Uniform duals V86 V6.16.16 V(6.8)2 V8.12.12 V68 V4.6.4.8 V4.12.16 Alternations [1+ ,8,6] [8+ ,6] [8,1+ ,6] [8,6+ ] [8,6,1+ ] [(8,6,2+ )] [8,6]+ h{8,6} s{8,6} hr{8,6} s{6,8} h{6,8} hrr{8,6} sr{8,6} Alternation duals V(4.6)6 V3.3.8.3.8.3 V(3.4.4.4)2 V3.4.3.4.3.6 V(3.8)8 V3.45 V3.3.6.3.8
Группа (7 7 2) треугольников , группа Кокстера [7,7], орбифолд (*772) содержит эти равномерные мозаики:
показывать Однородные семигептагональные мозаики Symmetry: [7,7], (*772) [7,7]+ , (772) {7,7} t{7,7} r{7,7} 2t{7,7}=t{7,7} 2r{7,7}={7,7} rr{7,7} tr{7,7} sr{7,7} Uniform duals V77 V7.14.14 V7.7.7.7 V7.14.14 V77 V4.7.4.7 V4.14.14 V3.3.7.3.7
Группа (8 8 2) треугольников , группа Кокстера [8,8], орбифолд (*882) содержит эти равномерные мозаики:
показывать Однородные восьмиугольные плитки Symmetry: [8,8], (*882) {8,8} t{8,8} r{8,8} 2t{8,8}=t{8,8} 2r{8,8}={8,8} rr{8,8} tr{8,8} Uniform duals V88 V8.16.16 V8.8.8.8 V8.16.16 V88 V4.8.4.8 V4.16.16 Alternations [1+ ,8,8] [8+ ,8] [8,1+ ,8] [8,8+ ] [8,8,1+ ] [(8,8,2+ )] [8,8]+ h{8,8} s{8,8} hr{8,8} s{8,8} h{8,8} hrr{8,8} sr{8,8} Alternation duals V(4.8)8 V3.4.3.8.3.8 V(4.4)4 V3.4.3.8.3.8 V(4.8)8 V46 V3.3.8.3.8
Существует бесконечно много общих групп треугольников семейств ( p q r ). В этой статье показаны однородные мозаики в 9 семействах: (4 3 3), (4 4 3), (4 4 4), (5 3 3), (5 4 3), (5 4 4), (6 3 3). , (6 4 3) и (6 4 4).
Группа (4 3 3) треугольников , группа Кокстера [(4,3,3)], орбифолд (*433) содержит эти равномерные мозаики. Без прямых углов в основном треугольнике конструкции Витгофа немного отличаются. Например, в семействе треугольников (4,3,3) форма имеет курносая шесть многоугольников вокруг вершины, а ее двойственная форма имеет шестиугольники, а не пятиугольники. В общем, вершинная фигура курносой мозаики в треугольнике ( p , q , r ) равна p. 3.q.3.r.3, в данном случае ниже 4.3.3.3.3.3.
Равномерные (4,3,3) мозаики скрывать Симметрия: [(4,3,3)], (*433) [(4,3,3)] + , (433) ч{8,3} 0 (4,3,3) г{3,8} 1 / 2 0,1 (4.3.3) ч{8,3} 1 (4,3,3) ч 2 {8,3} 1,2 (4,3,3) {3,8} 1 / 2 2 (4,3,3) ч 2 {8,3} 0,2 (4.3.3) т{3,8} 1 / 2 0,1,2 (4,3,3) с{3,8} 1 / 2 Униформа дуалы V(3.4) 3 В3.8.3.8 V(3.4) 3 Версия 3.6.4.6 V(3.3) 4 Версия 3.6.4.6 Версия 6.6.8 В3.3.3.3.3.4
Группа (4 4 3) треугольников , группа Кокстера [(4,4,3)], орбифолд (*443) содержит эти равномерные мозаики.
показывать Равномерные (4,4,3) мозаики Symmetry: [(4,4,3)] (*443) [(4,4,3)]+ [(4,4,3+ )] [(4,1+ ,4,3)] h{6,4} 0 (4,4,3)h2 {6,4} 0,1 (4,4,3){4,6}1 /2 1 (4,4,3)h2 {6,4}1,2 (4,4,3) h{6,4}2 (4,4,3) r{6,4}1 /2 0,2 (4,4,3)t{4,6}1 /2 0,1,2 (4,4,3)s{4,6}1 /2 hr{4,6}1 /2 h{4,6}1 /2 q{4,6} 1 (4,3,4)Uniform duals V(3.4)4 V3.8.4.8 V(4.4)3 V3.8.4.8 V(3.4)4 V4.6.4.6 V6.8.8 V3.3.3.4.3.4 V(4.4.3)2 V66 V4.3.4.6.6
Группа (4 4 4) треугольников , группа Кокстера [(4,4,4)], орбифолд (*444) содержит эти равномерные мозаики.
показывать Равномерные (4,4,4) мозаики Symmetry: [(4,4,4)], (*444) [(4,4,4)]+ [(1+ ,4,4,4)] [(4+ ,4,4)] t0 (4,4,4) t0,1 (4,4,4) 2 {8,4}t1 (4,4,4) 1 /2 t1,2 (4,4,4) 2 {8,4}t2 (4,4,4) t0,2 (4,4,4) 1 /2 t0,1,2 (4,4,4) 1 /2 s(4,4,4) 1 /2 h(4,4,4) 1 /2 hr(4,4,4) 1 /2 Uniform duals V(4.4)4 V4.8.4.8 V(4.4)4 V4.8.4.8 V(4.4)4 V4.8.4.8 V8.8.8 V3.4.3.4.3.4 V88 V(4,4)3
Группа (5 3 3) треугольников , группа Кокстера [(5,3,3)], орбифолд (*533) содержит эти равномерные мозаики.
показывать Равномерные (5,3,3) мозаики Symmetry: [(5,3,3)], (*533) [(5,3,3)]+ , (533) h{10,3} 0 (5,3,3)r{3,10}1 /2 0,1 (5,3,3)h{10,3} 1 (5,3,3)h2 {10,3} 1,2 (5,3,3){3,10}1 /2 2 (5,3,3)h2 {10,3} 0,2 (5,3,3)t{3,10}1 /2 0,1,2 (5,3,3)s{3,10}1 /2 0,1,2 (5,3,3)Uniform duals V(3.5)3 V3.10.3.10 V(3.5)3 V3.6.5.6 V(3.3)5 V3.6.5.6 V6.6.10 V3.3.3.3.3.5
Группа (5 4 3) треугольников , группа Кокстера [(5,4,3)], орбифолд (*543) содержит эти равномерные мозаики.
показывать Symmetry: [(5,4,3)], (*543) [(5,4,3)]+ , (543) t0 (5,4,3) t0,1 (5,4,3) t1 (5,4,3) t1,2 (5,4,3) t2 (5,4,3) t0,2 (5,4,3) t0,1,2 (5,4,3) s(5,4,3) Uniform duals V(3.5)4 V3.10.4.10 V(4.5)3 V3.8.5.8 V(3.4)5 V4.6.5.6 V6.8.10 V3.5.3.4.3.3
Группа (5 4 4) треугольников , группа Кокстера [(5,4,4)], орбифолд (*544) содержит эти равномерные мозаики.
показывать Равномерные (5,4,4) мозаики Symmetry: [(5,4,4)] [(5,4,4)]+ [(5+ ,4,4)] [(5,4,1+ ,4)] t0 (5,4,4) t0,1 (5,4,4) 1 /2 t1 (5,4,4) t1,2 (5,4,4) 2 {10,4}t2 (5,4,4) 1 /2 t0,2 (5,4,4) 2 {10,4}t0,1,2 (5,4,4) 1 /2 s(4,5,4) 1 /2 h(4,5,4) 1 /2 hr(4,5,4)1 /2 Uniform duals V(4.5)4 V4.10.4.10 V(4.5)4 V4.8.5.8 V(4.4)5 V4.8.5.8 V8.8.10 V3.4.3.4.3.5 V1010 V(4.4.5)2
Группа (6 3 3) треугольников , группа Кокстера [(6,3,3)], орбифолд (*633) содержит эти равномерные мозаики.
показывать Равномерные (6,3,3) мозаики Symmetry: [(6,3,3)], (*633) [(6,3,3)]+ , (633) t0 {(6,3,3)} t0,1 {(6,3,3)} 1 /2 t1 {(6,3,3)} t1,2 {(6,3,3)} 2 {12,3}t2 {(6,3,3)} 1 /2 t0,2 {(6,3,3)} 2 {12,3}t0,1,2 {(6,3,3)} 1 /2 s{(6,3,3)} 1 /2 Uniform duals V(3.6)3 V3.12.3.12 V(3.6)3 V3.6.6.6 V(3.3)6 V3.6.6.6 V6.6.12 V3.3.3.3.3.6
Группа (6 4 3) треугольников , группа Кокстера [(6,4,3)], орбифолд (*643) содержит эти равномерные мозаики.
показывать Symmetry: [(6,4,3)] [(6,4,3)]+ [(6,1+ ,4,3)] [(6,4,3+ )] t0 {(6,4,3)} t0,1 {(6,4,3)} t1 {(6,4,3)} t1,2 {(6,4,3)} t2 {(6,4,3)} t0,2 {(6,4,3)} t0,1,2 {(6,4,3)} s{(6,4,3)} h{(6,4,3)} hr{(6,4,3)} Uniform duals V(3.6)4 V3.12.4.12 V(4.6)3 V3.8.6.8 V(3.4)6 V4.6.6.6 V6.8.12 V3.6.3.4.3.3 V(3.6.6)3 V4.(3.4)3
Группа (6 4 4) треугольников , группа Кокстера [(6,4,4)], орбифолд (*644) содержит эти равномерные мозаики.
показывать Symmetry : [(6,4,4)], (*644)(644) (6,4,4) t0,1 (6,4,4) 1 /2 t1 (6,4,4) t1,2 (6,4,4) 2 {12,4}t2 (6,4,4) 1 /2 t0,2 (6,4,4) 2 {12,4}t0,1,2 (6,4,4) 1 /2 s(6,4,4)1 /2 Uniform duals V(4.6)4 V(4.12)2 V(4.6)4 V4.8.6.8 V412 V4.8.6.8 V8.8.12 V4.6.4.6.6.6
Сводка мозаик с конечными треугольными фундаментальными областями [ редактировать ] Для таблицы всех равномерных гиперболических мозаик с фундаментальными областями ( p q r ), где 2 ⩽ p , q , r ⩽ 8.
См. Шаблон: Таблица конечных треугольных гиперболических мозаик. Четырехугольная область имеет 9 позиций образующих точек, которые определяют равномерные мозаики. Фигуры вершин перечислены для общей орбифолдной симметрии * pqrs , с 2-угольными гранями, вырождающимися в ребра. Пример равномерного мозаики симметрии *3222 Четырехсторонние фундаментальные области также существуют в гиперболической плоскости, причем * 3222 орбифолд (обозначение [∞, 3, ∞] Кокстера) является наименьшим семейством. Существует 9 мест генерации для равномерного разбиения мозаики внутри четырехугольных доменов. Фигура вершины может быть извлечена из фундаментальной области в трех случаях (1) Угол, (2) Средний край и (3) Центр. Когда генерирующие точки представляют собой углы, примыкающие к углам порядка 2, в этих углах существуют вырожденные двуугольные грани {2}, но их можно игнорировать. Плоские и чередующиеся однородные мозаики также могут быть созданы (не показаны), если фигура вершин содержит только четные грани.
Диаграммы Кокстера четырехугольных областей рассматриваются как вырожденный граф тетраэдра , 2 из 6 ребер которого отмечены бесконечностью или пунктирными линиями. Логическое требование, чтобы хотя бы одно из двух параллельных зеркал было активным, ограничивает однородные случаи до 9, а другие кольцевые шаблоны недействительны.
показывать 64 2 6.4.4.4 2 46
Существует бесконечно много семейств групп треугольников, включая бесконечные порядки. В этой статье показаны равномерные мозаики в 9 семействах: (∞ 3 2), (∞ 4 2), (∞ ∞ 2), (∞ 3 3), (∞ 4 3), (∞ 4 4), (∞ ∞ 3). , (∞ ∞ 4) и (∞ ∞ ∞).
Идеальная (∞ 3 2) группа треугольников , группа Кокстера [∞,3], орбифолд (*∞32) содержит эти равномерные мозаики:
показывать Symmetry: [∞,3], (*∞32) [∞,3]+ [1+ ,∞,3] [∞,3+ ] {∞,3} t{∞,3} r{∞,3} t{3,∞} {3,∞} rr{∞,3} tr{∞,3} sr{∞,3} h{∞,3} h2 {∞,3} s{3,∞} Uniform duals V∞3 V3.∞.∞ V(3.∞)2 V6.6.∞ V3∞ V4.3.4.∞ V4.6.∞ V3.3.3.3.∞ V(3.∞)3 V3.3.3.3.3.∞
Идеальная (∞ 4 2) группа треугольников , группа Кокстера [∞,4], орбифолд (*∞42) содержит эти равномерные мозаики:
показывать {∞,4} t{∞,4} r{∞,4} 2t{∞,4}=t{4,∞} 2r{∞,4}={4,∞} rr{∞,4} tr{∞,4} Dual figures V∞4 V4.∞.∞ V(4.∞)2 V8.8.∞ V4∞ V43 .∞ V4.8.∞ Alternations [1+ ,∞,4] [∞+ ,4] [∞,1+ ,4] [∞,4+ ] [∞,4,1+ ] [(∞,4,2+ )] [∞,4]+ h{∞,4} s{∞,4} hr{∞,4} s{4,∞} h{4,∞} hrr{∞,4} s{∞,4} Alternation duals V(∞.4)4 V3.(3.∞)2 V(4.∞.4)2 V3.∞.(3.4)2 V∞∞ V∞.44 V3.3.4.3.∞
Идеальная (∞ 5 2) группа треугольников , группа Кокстера [∞,5], орбифолд (*∞52) содержит эти равномерные мозаики:
показывать Symmetry: [∞,5], (*∞52) [∞,5]+ [1+ ,∞,5] [∞,5+ ] {∞,5} t{∞,5} r{∞,5} 2t{∞,5}=t{5,∞} 2r{∞,5}={5,∞} rr{∞,5} tr{∞,5} sr{∞,5} h{∞,5} h2 {∞,5} s{5,∞} Uniform duals V∞5 V5.∞.∞ V5.∞.5.∞ V∞.10.10 V5∞ V4.5.4.∞ V4.10.∞ V3.3.5.3.∞ V(∞.5)5 V3.5.3.5.3.∞
Идеальная (∞ ∞ 2) группа треугольников , группа Кокстера [∞, ∞], орбифолд (*∞∞2) содержит эти равномерные мозаики:
показывать {∞,∞} t{∞,∞} r{∞,∞} 2t{∞,∞}=t{∞,∞} 2r{∞,∞}={∞,∞} rr{∞,∞} tr{∞,∞} Dual tilings V∞∞ V∞.∞.∞ V(∞.∞)2 V∞.∞.∞ V∞∞ V4.∞.4.∞ V4.4.∞ Alternations [1+ ,∞,∞] [∞+ ,∞] [∞,1+ ,∞] [∞,∞+ ] [∞,∞,1+ ] [(∞,∞,2+ )] [∞,∞]+ h{∞,∞} s{∞,∞} hr{∞,∞} s{∞,∞} h2 {∞,∞} hrr{∞,∞} sr{∞,∞} Alternation duals V(∞.∞)∞ V(3.∞)3 V(∞.4)4 V(3.∞)3 V∞∞ V(4.∞.4)2 V3.3.∞.3.∞
Идеальная (∞ 3 3) группа треугольников , группа Кокстера [(∞,3,3)], орбифолд (*∞33) содержит эти равномерные мозаики.
показывать Symmetry: [(∞,3,3)], (*∞33) [(∞,3,3)]+ , (∞33) (∞,∞,3) t 0,1 (∞,3,3)t1 (∞,3,3) t1,2 (∞,3,3) t2 (∞,3,3) t0,2 (∞,3,3) t0,1,2 (∞,3,3) s(∞,3,3) Dual tilings V(3.∞)3 V3.∞.3.∞ V(3.∞)3 V3.6.∞.6 V(3.3)∞ V3.6.∞.6 V6.6.∞ V3.3.3.3.3.∞
Идеальная (∞ 4 3) группа треугольников , группа Кокстера [(∞,4,3)], орбифолд (*∞43) содержит эти равномерные мозаики:
показывать Symmetry: [(∞,4,3)] [(∞,4,3)]+ [(∞,4,3+ )] [(∞,1+ ,4,3)] (∞,4,3) t 0,1 (∞,4,3)t1 (∞,4,3) t1,2 (∞,4,3) t2 (∞,4,3) t0,2 (∞,4,3) t0,1,2 (∞,4,3) s(∞,4,3) ht0,2 (∞,4,3) ht1 (∞,4,3) Dual tilings V(3.∞)4 V3.∞.4.∞ V(4.∞)3 V3.8.∞.8 V(3.4)∞ 4.6.∞.6 V6.8.∞ V3.3.3.4.3.∞ V(4.3.4)2 .∞ V(6.∞.6)3
Идеальная (∞ 4 4) группа треугольников , группа Кокстера [(∞,4,4)], орбифолд (*∞44) содержит эти равномерные мозаики.
показывать Symmetry: [(4,4,∞)], (*44∞) (44∞) (4,4,∞) t 0,1 (4,4,∞)1 /2 t1 (4,4,∞)1 /2 t1,2 (4,4,∞)2 {∞,4} t2 (4,4,∞){4,∞}1 /2 t0,2 (4,4,∞)2 {∞,4} t0,1,2 (4,4,∞)t{4,∞}1 /2 s(4,4,∞)1 /2 Dual tilings V(4.∞)4 V4.∞.4.∞ V(4.∞)4 V4.∞.4.∞ V4∞ V4.∞.4.∞ V8.8.∞ V3.4.3.4.3.∞
Идеальная (∞ ∞ 3) группа треугольников , группа Кокстера [(∞, ∞,3)], орбифолд (*∞∞3) содержит эти равномерные мозаики.
показывать Symmetry: [(∞,∞,3)], (*∞∞3) [(∞,∞,3)]+ [(∞,∞,3+ )] [(∞,1+ ,∞,3)] (∞,∞,3) t 0,1 (∞,∞,3)2 {6,∞}t1 (∞,∞,3)1 /2 t1,2 (∞,∞,3)2 {6,∞} t2 (∞,∞,3) t0,2 (∞,∞,3)1 /2 t0,1,2 (∞,∞,3)1 /2 s(∞,∞,3)1 /2 hr0,2 (∞,∞,3)1 /2 hr1 (∞,∞,3)1 /2 Dual tilings V(3.∞)∞ V3.∞.∞.∞ V(∞.∞)3 V3.∞.∞.∞ V(3.∞)∞ V(6.∞)2 V6.∞.∞ V3.∞.3.∞.3.3 V(3.4.∞.4)2 V(∞.6)6
Идеальная (∞ ∞ 4) группа треугольников , группа Кокстера [(∞, ∞,4)], орбифолд (*∞∞4) содержит эти равномерные мозаики.
показывать Symmetry: [(∞,∞,4)], (*∞∞4) (∞,∞,4) t 0,1 (∞,∞,4)2 {8,∞}t1 (∞,∞,4) t1,2 (∞,∞,4)2 {∞,8} t2 (∞,∞,4) t0,2 (∞,∞,4) t0,1,2 (∞,∞,4) Dual tilings V(4.∞)∞ V∞.∞.∞.4 V∞4 V∞.∞.∞.4 V(4.∞)∞ V∞.∞.∞.4 V∞.∞.8 Alternations [(1+ ,∞,∞,4)] [(∞+ ,∞,4)] [(∞,1+ ,∞,4)] [(∞,∞+ ,4)] [(∞,∞,1+ ,4)] [(∞,∞,4+ )] [(∞,∞,4)]+ Alternation duals V∞∞ V∞.44 V(∞.4)4 V∞.44 V∞∞ V∞.44 V3.∞.3.∞.3.4
Идеальная (∞ ∞ ∞) группа треугольников , группа Кокстера [(∞, ∞, ∞)], орбифолд (*∞∞∞) содержит эти равномерные мозаики.
показывать (∞,∞,∞) r(∞,∞,∞) 2 {∞,∞}(∞,∞,∞) r(∞,∞,∞) 2 {∞,∞}(∞,∞,∞) r(∞,∞,∞) t(∞,∞,∞) Dual tilings V∞∞ V∞.∞.∞.∞ V∞∞ V∞.∞.∞.∞ V∞∞ V∞.∞.∞.∞ V∞.∞.∞ Alternations [(1+ ,∞,∞,∞)] [∞+ ,∞,∞)] [∞,1+ ,∞,∞)] [∞,∞+ ,∞)] [(∞,∞,∞,1+ )] [(∞,∞,∞+ )] [∞,∞,∞)]+ Alternation duals V(∞.∞)∞ V(∞.4)4 V(∞.∞)∞ V(∞.4)4 V(∞.∞)∞ V(∞.4)4 V3.∞.3.∞.3.∞
Краткое изложение мозаик с бесконечными треугольными фундаментальными областями [ редактировать ] Для таблицы всех равномерных гиперболических мозаик с фундаментальными областями ( p q r ), где 2 ≤ p , q , r ≤ 8 и один или несколько при ∞.
показывать (p q r) t0 h0 t01 h01 t1 h1 t12 h12 t2 h2 t02 h02 t012 s t0 {∞,3} 3 h0 {∞,3}3 t01 {∞,3} t1 {∞,3}2 t12 {∞,3} h12 {∞,3} t2 {∞,3} ∞ t02 {∞,3} t012 {∞,3} s{∞,3} t0 {∞,4} 4 h0 {∞,4}4 t01 {∞,4} h01 {∞,4} t1 {∞,4}2 h1 {∞,4}2 t12 {∞,4} h12 {∞,4} t2 {∞,4} ∞ h2 {∞,4}∞ t02 {∞,4} h02 {∞,4} t012 {∞,4} s{∞,4} t0 {∞,5} 5 h0 {∞,5}5 t01 {∞,5} t1 {∞,5}2 t12 {∞,5} h12 {∞,5} t2 {∞,5} ∞ t02 {∞,5} t012 {∞,5} s{∞,5} t0 {∞,6} 6 h0 {∞,6}6 t01 {∞,6} h01 {∞,6} t1 {∞,6} 2 h1 {∞,6}2 t12 {∞,6} h12 {∞,6} t2 {∞,6} ∞ h2 {∞,6}∞ t02 {∞,6} h02 {∞,6} t012 {∞,6} s{∞,6} t0 {∞,7} 7 h0 {∞,7}7 t01 {∞,7} t1 {∞,7} 2 t12 {∞,7} h12 {∞,7} t2 {∞,7} ∞ t02 {∞,7} t012 {∞,7} s{∞,7} t0 {∞,8} 8 h0 {∞,8}8 t01 {∞,8} h01 {∞,8} t1 {∞,8} 2 h1 {∞,8}2 t12 {∞,8} h12 {∞,8} t2 {∞,8} ∞ h2 {∞,8}∞ t02 {∞,8} h02 {∞,8} t012 {∞,8} s{∞,8} t0 {∞,∞} ∞ h0 {∞,∞}∞ t01 {∞,∞} h01 {∞,∞} t1 {∞,∞} 4 h1 {∞,∞}4 t12 {∞,∞} h12 {∞,∞} t2 {∞,∞} ∞ h2 {∞,∞}∞ t02 {∞,∞} 2 h02 {∞,∞}2 t012 {∞,∞} s{∞,∞} t0 (∞,3,3)3 t01 (∞,3,3)2 t1 (∞,3,3)3 t12 (∞,3,3) t2 (∞,3,3)∞ t02 (∞,3,3) t012 (∞,3,3) s(∞,3,3) t0 (∞,4,3)4 t01 (∞,4,3) t1 (∞,4,3)3 h1 (∞,4,3)3 t12 (∞,4,3) t2 (∞,4,3)∞ t02 (∞,4,3) h02 (∞,4,3) t012 (∞,4,3) s(∞,4,3) t0 (∞,5,3)5 t01 (∞,5,3) t1 (∞,5,3)3 t12 (∞,5,3) t2 (∞,5,3)∞ t02 (∞,5,3) t012 (∞,5,3) s(∞,5,3) t0 (∞,6,3)6 t01 (∞,6,3) t1 (∞,6,3)3 h1 (∞,6,3)3 t12 (∞,6,3) t2 (∞,6,3)∞ t02 (∞,6,3) h02 (∞,6,3) t012 (∞,6,3) s(∞,6,3) t0 (∞,7,3)7 t01 (∞,7,3) t1 (∞,7,3)3 t12 (∞,7,3) t2 (∞,7,3)∞ t02 (∞,7,3) t012 (∞,7,3) s(∞,7,3) t0 (∞,8,3)8 t01 (∞,8,3) t1 (∞,8,3)3 h1 (∞,8,3)3 t12 (∞,8,3) t2 (∞,8,3)∞ t02 (∞,8,3) h02 (∞,8,3) t012 (∞,8,3) s(∞,8,3) t0 (∞,∞,3)∞ t01 (∞,∞,3) t1 (∞,∞,3)6 h1 (∞,∞,3)6 t12 (∞,∞,3) t2 (∞,∞,3)∞ t02 (∞,∞,3)2 h02 (∞,∞,3)2 t012 (∞,∞,3) s(∞,∞,3) t0 (∞,4,4)4 h0 (∞,4,4)4 t01 (∞,4,4)2 h01 (∞,4,4)2 t1 (∞,4,4)4 h1 (∞,4,4)4 t12 (∞,4,4) h12 (∞,4,4) t2 (∞,4,4)∞ h2 (∞,4,4)∞ t02 (∞,4,4) h02 (∞,4,4) t012 (∞,4,4) s(∞,4,4) t0 (∞,5,4)5 h0 (∞,5,4)5 t01 (∞,5,4) t1 (∞,5,4)4 t12 (∞,5,4) h12 (∞,5,4) t2 (∞,5,4)∞ t02 (∞,5,4) t012 (∞,5,4) s(∞,5,4) t0 (∞,6,4)6 h0 (∞,6,4)6 t01 (∞,6,4) h01 (∞,6,4) t1 (∞,6,4)4 h1 (∞,6,4)4 t12 (∞,6,4) h12 (∞,6,4) t2 (∞,6,4)∞ h2 (∞,6,4)∞ t02 (∞,6,4) h02 (∞,6,4) t012 (∞,6,4) s(∞,6,4) t0 (∞,7,4)7 h0 (∞,7,4)7 t01 (∞,7,4) t1 (∞,7,4)4 t12 (∞,7,4) h12 (∞,7,4) t2 (∞,7,4)∞ t02 (∞,7,4) t012 (∞,7,4) s(∞,7,4) t0 (∞,8,4)8 h0 (∞,8,4)8 t01 (∞,8,4) h01 (∞,8,4) t1 (∞,8,4)4 h1 (∞,8,4)4 t12 (∞,8,4) h12 (∞,8,4) t2 (∞,8,4)∞ h2 (∞,8,4)∞ t02 (∞,8,4) h02 (∞,8,4) t012 (∞,8,4) s(∞,8,4) t0 (∞,∞,4)∞ h0 (∞,∞,4)∞ t01 (∞,∞,4) h01 (∞,∞,4) t1 (∞,∞,4)8 h1 (∞,∞,4)8 t12 (∞,∞,4) h12 (∞,∞,4) t2 (∞,∞,4)∞ h2 (∞,∞,4)∞ t02 (∞,∞,4)2 h02 (∞,∞,4)2 t012 (∞,∞,4) s(∞,∞,4) t0 (∞,5,5)5 t01 (∞,5,5)2 t1 (∞,5,5)5 t12 (∞,5,5) t2 (∞,5,5)∞ t02 (∞,5,5) t012 (∞,5,5) s(∞,5,5) t0 (∞,6,5)6 t01 (∞,6,5) t1 (∞,6,5)5 h1 (∞,6,5)5 t12 (∞,6,5) t2 (∞,6,5)∞ t02 (∞,6,5) h02 (∞,6,5) t012 (∞,6,5) s(∞,6,5) t0 (∞,7,5)7 t01 (∞,7,5) t1 (∞,7,5)5 t12 (∞,7,5) t2 (∞,7,5)∞ t02 (∞,7,5) t012 (∞,7,5) s(∞,7,5) t0 (∞,8,5)8 t01 (∞,8,5) t1 (∞,8,5)5 h1 (∞,8,5)5 t12 (∞,8,5) t2 (∞,8,5)∞ t02 (∞,8,5) h02 (∞,8,5) t012 (∞,8,5) s(∞,8,5) t0 (∞,∞,5)∞ t01 (∞,∞,5) t1 (∞,∞,5)10 h1 (∞,∞,5)10 t12 (∞,∞,5) t2 (∞,∞,5)∞ t02 (∞,∞,5)2 h02 (∞,∞,5)2 t012 (∞,∞,5) s(∞,∞,5) t0 (∞,6,6)6 h0 (∞,6,6)6 t01 (∞,6,6)2 h01 (∞,6,6)2 t1 (∞,6,6)6 h1 (∞,6,6)6 t12 (∞,6,6) h12 (∞,6,6) t2 (∞,6,6)∞ h2 (∞,6,6)∞ t02 (∞,6,6) h02 (∞,6,6) t012 (∞,6,6) s(∞,6,6) t0 (∞,7,6)7 h0 (∞,7,6)7 t01 (∞,7,6) t1 (∞,7,6)6 t12 (∞,7,6) h12 (∞,7,6) t2 (∞,7,6)∞ t02 (∞,7,6) t012 (∞,7,6) s(∞,7,6) t0 (∞,8,6)8 h0 (∞,8,6)8 t01 (∞,8,6) h01 (∞,8,6) t1 (∞,8,6)6 h1 (∞,8,6)6 t12 (∞,8,6) h12 (∞,8,6) t2 (∞,8,6)∞ h2 (∞,8,6)∞ t02 (∞,8,6) h02 (∞,8,6) t012 (∞,8,6) s(∞,8,6) t0 (∞,∞,6)∞ h0 (∞,∞,6)∞ t01 (∞,∞,6) h01 (∞,∞,6) t1 (∞,∞,6)12 h1 (∞,∞,6)12 t12 (∞,∞,6) h12 (∞,∞,6) t2 (∞,∞,6)∞ h2 (∞,∞,6)∞ t02 (∞,∞,6)2 h02 (∞,∞,6)2 t012 (∞,∞,6) s(∞,∞,6) t0 (∞,7,7)7 t01 (∞,7,7)2 t1 (∞,7,7)7 t12 (∞,7,7) t2 (∞,7,7)∞ t02 (∞,7,7) t012 (∞,7,7) s(∞,7,7) t0 (∞,8,7)8 t01 (∞,8,7) t1 (∞,8,7)7 h1 (∞,8,7)7 t12 (∞,8,7) t2 (∞,8,7)∞ t02 (∞,8,7) h02 (∞,8,7) t012 (∞,8,7) s(∞,8,7) t0 (∞,∞,7)∞ t01 (∞,∞,7) t1 (∞,∞,7)14 h1 (∞,∞,7)14 t12 (∞,∞,7) t2 (∞,∞,7)∞ t02 (∞,∞,7)2 h02 (∞,∞,7)2 t012 (∞,∞,7) s(∞,∞,7) t0 (∞,8,8)8 h0 (∞,8,8)8 t01 (∞,8,8)2 h01 (∞,8,8)2 t1 (∞,8,8)8 h1 (∞,8,8)8 t12 (∞,8,8) h12 (∞,8,8) t2 (∞,8,8)∞ h2 (∞,8,8)∞ t02 (∞,8,8) h02 (∞,8,8) t012 (∞,8,8) s(∞,8,8) t0 (∞,∞,8)∞ h0 (∞,∞,8)∞ t01 (∞,∞,8) h01 (∞,∞,8) t1 (∞,∞,8)16 h1 (∞,∞,8)16 t12 (∞,∞,8) h12 (∞,∞,8) t2 (∞,∞,8)∞ h2 (∞,∞,8)∞ t02 (∞,∞,8)2 h02 (∞,∞,8)2 t012 (∞,∞,8) s(∞,∞,8) t0 (∞,∞,∞)∞ h0 (∞,∞,∞)∞ t01 (∞,∞,∞)2 h01 (∞,∞,∞)2 t1 (∞,∞,∞)∞ h1 (∞,∞,∞)∞ t12 (∞,∞,∞)2 h12 (∞,∞,∞)2 t2 (∞,∞,∞)∞ h2 (∞,∞,∞)∞ t02 (∞,∞,∞)2 h02 (∞,∞,∞)2 t012 (∞,∞,∞)3 s(∞,∞,∞)3