Треугольник Шварца

Герман Шварц , ок. 1890 г.

В геометрии треугольник Шварца , названный в честь Германа Шварца , представляет собой сферический треугольник , который можно использовать для мозаики сферы . ( сферическая мозаика ), возможно, перекрывающейся, посредством отражений в ее краях Они были классифицированы Шварцем (1873) .

В более общем смысле их можно определить как мозаику сферы, евклидовой плоскости или гиперболической плоскости . Каждый треугольник Шварца на сфере определяет конечную группу , а на евклидовой или гиперболической плоскости они определяют бесконечную группу.

Треугольник Шварца представлен тремя рациональными числами ( p q r ) , каждое из которых представляет угол в вершине. Значение n ⁄ d означает, что угол при вершине равен d ⁄ n полукруга. «2» означает прямоугольный треугольник . Когда это целые числа, треугольник называется треугольником Мёбиуса и соответствует непересекающейся мозаике, а группа симметрии называется группой треугольников . В сфере имеется три треугольника Мёбиуса плюс одно однопараметрическое семейство; на плоскости имеются три треугольника Мёбиуса, а в гиперболическом пространстве существует трёхпараметрическое семейство треугольников Мёбиуса и нет исключительных объектов .

Пространство решений

Фундаментальный треугольник домена ( pqr ) с углами при вершинах π ⁄ p , π ⁄ q и π ⁄ r , может существовать в разных пространствах в зависимости от значения суммы обратных чисел этих целых чисел:

$${\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}\quad {\begin{cases}>1&\implies {\text{Sphere}}\\[2pt]=1&\implies {\text{Euclidean plane}}\\[2pt]<1&\implies {\text{Hyperbolic plane}}\end{cases}}$$

Это просто способ сказать, что в евклидовом пространстве сумма внутренних углов треугольника равна π , тогда как на сфере они дают угол, больший, чем π , а в гиперболическом пространстве — меньший.

Графическое представление

Треугольник Шварца графически изображается треугольным графиком . Каждый узел представляет собой ребро (зеркало) треугольника Шварца. Каждое ребро помечается рациональным значением, соответствующим порядку отражения, т.е. π/ угол вершины .

Черный треугольник ( p q r ) на сфере

График треугольника Шварца

Края второго порядка представляют собой перпендикулярные зеркала, которые на этой диаграмме можно игнорировать. Диаграмма Коксетера-Динкина представляет собой этот треугольный граф со скрытыми ребрами второго порядка.

Группу Кокстера можно использовать для более простых обозначений, например ( p q r ) для циклических графов и ( p q 2) = [ p , q ] для (прямоугольных треугольников) и ( p 2 2) = [ p ]× [].

Список треугольников Шварца

Треугольники Мёбиуса для сферы

(2 2 2) или [2,2]	(3 2 2) или [3,2]	...
(3 3 2) или [3,3]	(4 3 2) или [4,3]	(5 3 2) или [5,3]

Треугольники Шварца с целыми числами, также называемые треугольниками Мёбиуса , включают одно 1-параметрическое семейство и три исключительных случая:

1. [ p ,2] или ( p 2 2) – двугранная симметрия ,
2. [3,3] или (3 3 2) – тетраэдрическая симметрия ,
3. [4,3] или (4 3 2) – Октаэдрическая симметрия ,
4. [5,3] или (5 3 2) – икосаэдрическая симметрия ,

Треугольники Шварца для сферы по плотности

Треугольники Шварца ( p q r ), сгруппированные по плотности :

Плотность	двугранный	Тетраэдрический	Октаэдрический	икосаэдрический
д	( 2 2 н / д )
1		( 2 3 3)	( 2 3 4)	( 2 3 5)
2		(3/2 3 3)	(3/2 4 4)	(3/2 5 5), (5/2 3 3)
3		( 2 3/2 3)		( 2 5/2 5)
4			(3 4/3 4)	(3 5/3 5)
5		( 2 3/2 3/2)	( 2 3/2 4)
6		(3/2 3/2 3/2)		(5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7			( 2 3 4/3)	( 2 3 5/2)
8				(3/2 5/2 5)
9				( 2 5/3 5)
10				(3 5/3 5/2), (3 5/4 5)
11			( 2 3/2 4/3)	( 2 3/2 5)
13				( 2 3 5/3)
14			(3/2 4/3 4/3)	(3/2 5/2 5/2), (3 3 5/4)
16				(3 5/4 5/2)
17				( 2 3/2 5/2)
18				(3/2 3 5/3), (5/3 5/3 5/2)
19				( 2 3 5/4)
21				( 2 5/4 5/2)
22				(3/2 3/2 5/2)
23				( 2 3/2 5/3)
26				(3/2 5/3 5/3)
27				( 2 5/4 5/3)
29				( 2 3/2 5/4)
32				(3/2 5/4 5/3)
34				(3/2 3/2 5/4)
38				(3/2 5/4 5/4)
42				(5/4 5/4 5/4)

Треугольники для евклидовой плоскости

(3 3 3)

(4 4 2)

(6 3 2)

Плотность 1:

1. (3 3 3) – 60-60-60 ( равносторонние ),
2. (4 4 2) – 45-45-90 (равнобедренная правая),
3. (6 3 2) – 30-60-90 ,

Плотность 2:

1. (6 6 3/2) — треугольник 120-30-30

Плотность ∞:

1. (4 4/3 ∞)
2. (3 3/2 ∞)
3. (6 6/5 ∞)

Треугольники для гиперболической плоскости

(7 3 2)	(8 3 2)	(5 4 2)
(4 3 3)	(4 4 3)	(∞ ∞ ∞)
Основные области треугольников ( p q r )

Плотность 1:

• (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
• (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
• (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
• (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
• (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
• (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
• (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
• (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
• ...
• (∞ ∞ ∞)

Плотность 2:

• (3/2 7 7), (3/2 8 8), (3/2 9 9) ... (3/2 ∞ ∞)
• (5/2 4 4), (5/2 5 5), (5/2 6 6) ... (5/2 ∞ ∞)
• (7/2 3 3), (7/2 4 4), (7/2 5 5) ... (7/2 ∞ ∞)
• (9/2 3 3), (9/2 4 4), (9/2 5 5) ... (9/2 ∞ ∞)
• ...

Плотность 3:

• (2 7/2 7), (2 9/2 9), (2 11/2 11) ...

Плотность 4:

• (7/3 3 7), (8/3 3 8), (3 10/3 10), (3 11/3 11) ...

Плотность 6:

• (7/4 7 7), (9/4 9 9), (11/4 11 11) ...
• (7/2 7/2 7/2), (9/2 9/2 9/2), ...

Плотность 10:

• (3 7/2 7)

Треугольник Шварца (2 3 7) является наименьшим гиперболическим треугольником Шварца и поэтому представляет особый интерес. Его группа треугольников (или, точнее, группа фон Дейка индекса 2 изометрий, сохраняющих ориентацию) — это (2,3,7) группа треугольников , которая является универсальной группой для всех групп Гурвица — максимальных групп изометрий римановых поверхностей . Все группы Гурвица являются факторами группы треугольников (2,3,7), а все поверхности Гурвица замощены треугольником Шварца (2,3,7). Наименьшая группа Гурвица — это простая группа порядка 168, вторая наименьшая неабелева простая группа , изоморфная PSL(2,7) , а соответствующая поверхность Гурвица (рода 3) — квартика Клейна .

Треугольник (2 3 8) замощает поверхность Больца , высокосимметричную (но не Гурвиц) поверхность рода 2.

Перечисленные выше треугольники с одним нецелым углом были впервые классифицированы Энтони В. Кнаппом . Список треугольников с кратными нецелыми углами приведен в .

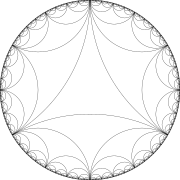
Тесселяция треугольниками Шварца

В этом разделе с использованием элементарных методов будет обсуждаться замощение гиперболической верхней полуплоскости треугольниками Шварца. элементарный подход Каратеодори (1954) Для треугольников без «каспов» — углов, равных нулю или, что эквивалентно, вершин на действительной оси — будет использоваться . Для треугольников с одной или двумя точками возврата будут использоваться элементарные рассуждения Эванса (1973) , упрощающие подход Хекке (1935) : в случае треугольника Шварца с одним углом нулевым, а другим прямым углом, сохраняется ориентация Подгруппа группы отражения треугольника является группой Гекке . Для идеального треугольника, в котором все углы равны нулю, так что все вершины лежат на вещественной оси, существование мозаики будет установлено путем соотнесения ее с рядом Фейри, описанным в Hardy & Wright (2008) и Series (2015) . В этом случае мозаику можно рассматривать как мозаику, связанную с тремя соприкасающимися кругами на сфере Римана , предельный случай конфигураций, связанных с тремя непересекающимися невложенными кругами и их группами отражений, так называемую « Группы Шоттки », подробно описанные в Mumford, Series & Wright (2015) . Альтернативно — разделив идеальный треугольник на шесть треугольников с углами 0, π /2 и π /3 — мозаику идеальными треугольниками можно понять с точки зрения мозаика треугольниками с одной или двумя вершинами.

Треугольники без точек пересечения

Мозаика треугольниками с углами π /4, π /4 и π /5.

Мозаика треугольниками с углами π /3, π /5 и ​​π /7.

Мозаика равносторонними треугольниками с углами π /4

Предположим, что гиперболический треугольник Δ имеет углы π / a , π / b и π / c с целыми числами a , b , c больше 1. Гиперболическая площадь треугольника Δ равна π – π / a – π / b – π / c , так что

${\frac {1}{a}}+{\frac {1}{b}}+{\frac {1}{c}}<1.$

Построение мозаики сначала будет осуществляться для случая, когда a , b и c больше 2.

Исходный треугольник Δ дает выпуклый многоугольник P ₁ с 3 вершинами. В каждой из трех вершин треугольник можно последовательно отразить через ребра, исходящие из вершин, чтобы создать 2 млн копий треугольника, где угол в вершине равен π / m . Треугольники не перекрываются, за исключением краев, половина из них имеет обратную ориентацию и совмещается, образуя мозаику окрестностей точки. Объединение этих новых треугольников вместе с исходным треугольником образует связную фигуру P ₂ . Он состоит из треугольников, которые пересекаются только по краям или вершинам, образует выпуклый многоугольник со всеми углами, меньшими или равными π , и каждая сторона является ребром отраженного треугольника. В случае, когда угол Δ равен π /3, вершина P ₂ будет иметь внутренний угол π , но это не влияет на выпуклость P ₂ . Даже в этом вырожденном случае, когда возникает угол π , два коллинеарных края по-прежнему считаются различными для целей построения.

Построение P ₂ можно понять более ясно, заметив, что некоторые треугольники или плитки добавляются дважды, причем три из них имеют общую сторону с исходным треугольником. Остальные имеют только одну общую вершину. Более систематический способ укладки мозаики — сначала добавить по плитке к каждой стороне (отражение треугольника на этом ребре), а затем заполнить промежутки в каждой вершине. В результате всего получается 3 + (2 a – 3) + (2 b – 3) + (2 c – 3) = 2( a + b + c ) – 6 новых треугольников. Новые вершины бывают двух типов. Те, которые являются вершинами треугольников, прикрепленных к сторонам исходного треугольника, которые соединены с двумя вершинами Δ. Каждый из них лежит в трех новых треугольниках, пересекающихся в этой вершине. Остальные соединены с единственной вершиной треугольника Δ и принадлежат двум новым треугольникам, имеющим общее ребро. Таким образом, имеется 3 + (2 a – 4) + (2 b – 4) + (2 c – 4) = 2( a + b + c ) – 9 новых вершин. По конструкции перекрытия отсутствуют. Чтобы увидеть, что P ₂ выпукла, достаточно увидеть, что угол между сторонами, сходящимися в новой вершине, составляет угол, меньший или равный π . Но новые вершины лежат в двух или трех новых треугольниках, которые пересекаются в этой вершине, поэтому угол в этой вершине не превышает 2 π /3 или π , как и требуется.

Этот процесс можно повторить для P2 _, чтобы получить , _{сначала} добавляя плитки к каждому краю P2 _, а затем заполняя плитки вокруг каждой вершины P2 _P3 . Затем процесс можно повторить от P ₃ , чтобы получить P ₄ и так далее, последовательно производя P _n из P _{n – 1} . Индуктивно можно проверить, что все это выпуклые многоугольники с непересекающимися плитками.Действительно, как и на первом этапе процесса, при построении P _n из P _{n – 1} существует два типа плиток : те, которые прикреплены к ребру P _{n – 1} , и те, которые прикреплены к одной вершине. Аналогично, существует два типа вершин: в одной встречаются две новые плитки, а в другой — три плитки. Таким образом, при условии, что плитки не перекрываются, предыдущий аргумент показывает, что углы при вершинах не превышают π и, следовательно, P _n — выпуклый многоугольник.

Поэтому необходимо убедиться, что при построении P _n из P _{n − 1} :

(a) новые треугольники не перекрываются с P _{n − 1,} за исключением случаев, уже описанных;

(б) новые треугольники не перекрываются друг с другом, за исключением случаев, уже описанных;

(в) геодезическая из любой точки Δ до вершины многоугольника P _{n – 1} составляет угол ≤ 2 π /3 с каждым из ребер многоугольника в этой вершине.

Чтобы доказать (а), заметим, что по выпуклости многоугольник P _{n − 1} является пересечением выпуклых полупространств, определяемых полными дугами окружностей, определяющими его границу. Таким образом, в данной вершине P _{n − 1} находятся две такие дуги окружности, определяющие два сектора: один сектор содержит внутренность P _{n − 1} , другой содержит внутренности новых треугольников, добавленных вокруг данной вершины. Это можно визуализировать, используя преобразование Мёбиуса, чтобы сопоставить верхнюю полуплоскость с единичным диском, а вершину с началом координат; внутренняя часть многоугольника и каждый из новых треугольников лежат в разных секторах единичного круга. Таким образом, (а) доказано.

Прежде чем доказывать (c) и (b), можно применить преобразование Мёбиуса, чтобы сопоставить верхнюю полуплоскость с единичным кругом, а фиксированную точку внутри Δ — с началом координат.

Доказательство (в) проводится по индукции. Обратите внимание, что радиус, соединяющий начало координат с вершиной многоугольника P _{n − 1,} образует угол меньше 2 π /3 с каждым из ребер многоугольника в этой вершине, если ровно два треугольника из P _{n − 1} пересекаются в вершине. вершине, поскольку каждый из них имеет угол, меньший или равный π /3 в этой вершине. Чтобы проверить, верно ли это, когда три треугольника P _{n − 1} встречаются в вершине, скажем, C , предположим, что основание среднего треугольника находится на стороне AB из P _{n − 2} . Радиусы OA и OB углы, меньшие или равные 2π / по индукции образуют с ребром AB 3 . В этом случае область в секторе между радиусами ОА и ОВ вне ребра AB является выпуклой как пересечение трех выпуклых областей. По индукции углы A и B больше или равны π /3. Таким образом, геодезические, ведущие к C из A и B, начинаются в этом регионе; по выпуклости треугольник ABC целиком лежит внутри области. Четырехугольник OACB имеет все углы меньше π (поскольку OAB — геодезический треугольник), поэтому он выпуклый. Следовательно, радиус OC угла треугольника ABC вблизи C. лежит внутри Таким образом, углы между OC и двумя краями P _{n – 1,} встречающимися в точке C, меньше или равны π /3 + π /3 = 2 π /3, как утверждается.

Для доказательства (б) надо проверить, как пересекаются новые треугольники Pn _в .

Сначала рассмотрим плитки, добавленные к краям P _{n – 1} . Приняв обозначения, аналогичные (c), пусть AB — основание плитки, а C — третья вершина. Тогда радиусы OA и OB углы, меньшие или равные 2 π образуют с ребром AB /3 , и рассуждения доказательства (c) применимы для доказательства того, что треугольник ABC лежит внутри сектора, определяемого радиусами OA и OB. . Это верно для каждого ребра P _{n – 1} . Поскольку внутренности секторов, определяемых отдельными ребрами, не пересекаются, новые треугольники этого типа пересекаются только так, как утверждается.

Далее рассмотрим дополнительные плитки, добавленные для каждой вершины P _{n – 1} . Если считать вершину A , то три — это два ребра AB ₁ и AB ₂ из P _{n – 1,} пересекаются в A. которые Пусть C ₁ и C ₂ — дополнительные вершины плиток, добавленных к этим ребрам. Теперь дополнительные плитки, добавленные в A , лежат в секторе, определенном радиусами OB ₁ и OB ₂ . Многоугольник с вершинами C ₂ O , C ₁ , а затем вершинами дополнительных плиток имеет все внутренние углы меньше π и, следовательно, является выпуклым. Следовательно, он полностью содержится в секторе, определяемом радиусами OC ₁ и OC ₂ . Поскольку внутренности этих секторов не пересекаются, это подразумевает все утверждения о том, как пересекаются добавленные плитки.

Мозаика треугольниками с углами π /2, π /3 и π /7.

Мозаика треугольниками с углами π /2, π /4 и π /5.

Наконец, осталось доказать, что замощение, образованное объединением треугольников, покрывает всю верхнюю полуплоскость. Любая точка z, мозаикой, лежит в многоугольнике и _Pn , следовательно, в многоугольнике Pn _{покрытая +1} . Следовательно, он лежит в копии исходного треугольника Δ, а также в копии P _{2 ,} полностью содержащейся в P _{n +1} . Гиперболическое расстояние между ∆ и внешностью P2 _меньше равно r > 0. Таким образом, гиперболическое расстояние между z и точками, не покрытыми мозаикой, не r . Поскольку это относится ко всем точкам замощения, множество, покрытое замощением, замкнуто. С другой стороны, замощение является открытым, поскольку оно совпадает с объединением внутренностей многоугольников P _n . Благодаря связности тесселяция должна охватывать всю верхнюю полуплоскость.

Чтобы понять, как действовать в случае, когда угол Δ является прямым, обратите внимание, что неравенство

${\frac {1}{a}}+{\frac {1}{b}}+{\frac {1}{c}}<1$.

подразумевает, что если один из углов прямой, скажем a = 2, то оба угла b и c больше 2 и один из них, скажем b , должен быть больше 3. В этом случае отражение треугольника через сторону AB дает равнобедренный гиперболический треугольник с углами π / c , π / c и 2 π / b . Если 2 π / b ≤ π /3, т.е. b больше 5, то все углы удвоенного треугольника меньше или равны π /3. В этом случае построение мозаики, приведенной выше, посредством увеличения выпуклых многоугольников слово в слово адаптируется к этому случаю, за исключением того, что вокруг вершины с углом 2 π / b требуется только b , а не 2 b, копии треугольника, чтобы замостить окрестность. вершины. Это возможно, поскольку удвоенный треугольник является равнобедренным. Тесселяция для удвоенного треугольника дает результат для исходного треугольника, если разрезать все большие треугольники пополам.

Осталось рассмотреть случай, когда b равно 4 или 5. Если b = 4, то c ≥ 5: в этом случае, если c ≥ 6, то b и c можно поменять местами, и применим приведенный выше аргумент, оставив случай b = 4. и c = 5. Если b = 5, то c ≥ 4. Случай c ≥ 6 можно решить, поменяв местами b и c , так что единственным дополнительным случаем будет b = 5 и c = 5. Этот последний равнобедренный треугольник является удвоенная версия первого исключительного треугольника, поэтому _{только этот треугольник Δ 1} — с углами π /2, π /4 и π /5 и ​​гиперболической площадью π необходимо рассматривать /20 (см. ниже). Каратеодори (1954) рассматривает этот случай с помощью общего метода, который работает для всех прямоугольных треугольников, у которых два других угла меньше или равны π /4. Предыдущий метод построения P ₂ , P ₃ , ... модифицируется добавлением дополнительного треугольника каждый раз, когда угол 3 π в вершине возникает /2. Те же рассуждения применимы для доказательства отсутствия перекрытия и того, что мозаика покрывает гиперболическую верхнюю полуплоскость.

С другой стороны, данная конфигурация порождает группу арифметических треугольников. Впервые они были изучены Фрике и Кляйном (1897) . и породили обширную литературу. В 1977 году Такеучи получил полную классификацию групп арифметических треугольников (их конечное число) и определил, когда две из них соизмеримы. Конкретный пример связан с кривой Бринга , и арифметическая теория подразумевает, что группа треугольников для Δ ₁ содержит группу треугольников для треугольника Δ ₂ с углами π / 4, π / 4 и π / 5 в качестве ненормальной подгруппы индекса. 6.

Удваивая треугольники Δ1 _и Δ2 _, это означает, что должна существовать связь между 6 треугольниками Δ3 _с углами π /2, π /5 и ​​π /5 и ​​гиперболической площадью π /10 и треугольником Δ4 _с углами π / 5, π /5 и ​​π /10 и гиперболическая площадь 3 π /5. Трелфолл (1932) установил такое соотношение непосредственно, совершенно элементарными геометрическими средствами, без обращения к теории арифметики: действительно, как показано на пятом рисунке ниже, четырехугольник, полученный отражением через сторону треугольника типа Δ _4, можно разложить по формуле 12 треугольников типа Δ ₃ . Мозаику треугольниками типа Δ ₄ можно выполнить основным методом этого раздела; следовательно, это доказывает существование мозаики треугольниками типа _∆3 и _∆1 .

• 
  Мозаика треугольниками с углами π /2, π /5 и ​​π /5.
• 
  Тесселяция, полученная путем объединения двух треугольников
• 
  Замощение пятиугольниками, образованными из 10 (2,5,5) треугольников.
• 
  Приспособление к замощению треугольниками с углами π /5, π /10, π /10
• 
  Укладка 2 (5,10,10) треугольников 12 (2,5,5) треугольниками

Треугольники с одной или двумя вершинами

В случае треугольника Шварца с одной или двумя точками возврата процесс замощения упрощается; но легче использовать другой метод, восходящий к Гекке, чтобы доказать, что они исчерпывают гиперболическую верхнюю полуплоскость.

В случае одного возврата и ненулевых углов π / a , π / b с целыми числами a , b больше единицы, мозаику можно представить в единичном круге с вершиной, имеющей угол π / a в начале координат. Укладка мозаики начинается с добавления 2–1 копий треугольника в начале координат путем последовательных отражений. В результате получается многоугольник P ₁ с 2 точками возврата и между каждыми двумя вершинами 2 a, каждая из которых имеет угол π / b . Следовательно, многоугольник выпуклый. Для каждой неидеальной вершины P ₁ уникальный треугольник с этой вершиной можно аналогично отразить вокруг этой вершины, добавив таким образом 2 b – 1 новых треугольников, 2 b – 1 новых идеальных точек и 2 b – 1 новых вершин с углом π. / а . Таким образом, полученный многоугольник P ₂ состоит из 2 a (2 b – 1) точек возврата и такого же количества вершин, каждая из которых имеет угол π / a , поэтому является выпуклым. Процесс можно продолжить таким образом, чтобы получить выпуклые многоугольники P ₃ , P ₄ и так далее. Многоугольник P _n будет иметь вершины с углами, чередующимися между 0 и π / a для четного n и между 0 и π / b для нечетного n . По конструкции треугольники перекрываются только по краям или вершинам, поэтому образуют мозаику.

• 
  Мозаика треугольником с углами 0, π /3, π /5
• 
  Мозаика треугольником с углами 0, π /5, π /2
• 
  Мозаика треугольником с углами 0, 0, π /5

Случай, когда треугольник имеет две вершины и один ненулевой угол π / a, можно свести к случаю одной вершины, заметив, что тринале является двойником треугольника с одной вершиной и ненулевыми углами π / a и π. / b с b = 2. Затем разбиение продолжается, как и раньше.

Чтобы доказать, что они дают мозаику, удобнее работать в верхней полуплоскости. Оба случая можно рассматривать одновременно, поскольку случай двух точек возврата получается удвоением треугольника с одной точкой возврата и ненулевыми углами π / a и π /2. Итак, рассмотрим геодезический треугольник в верхней полуплоскости с углами 0, π / a , π / b и целыми числами a , b, большими единицы. Внутренность такого треугольника можно представить как область X в верхней полуплоскости, лежащую вне единичного круга | г | ≤ 1 и между двумя прямыми, параллельными мнимой оси, проходящим через точки u и v на единичной окружности. Пусть Γ — группа треугольников, порожденная тремя отражениями на сторонах треугольника.

Чтобы доказать, что последовательные отражения треугольника покрывают верхнюю полуплоскость, достаточно показать, что для любого в верхней полуплоскости существует g в Γ такой, что g ( z ) лежит в X. z Это следует из аргумента Эванса (1973) , упрощенного из теории групп Гекке . Пусть λ = Re a и µ = Re b, так что, не ограничивая общности, λ < 0 ⩽ µ. Три отражения по сторонам определяются выражением

$R_{1}(z)={\frac {1}{\overline {z}}},\ R_{2}(z)=-{\overline {z}}+\lambda ,\ R_{3}(z)=-{\overline {z}}+\mu .$

Таким образом, T = R ₃ ∘ R ₂ является сдвигом на µ − λ. Отсюда следует, что для любого z ₁ в верхней полуплоскости существует элемент g ₁ в подгруппе Γ ₁ группы Γ, порожденный T такой, что w ₁ = g ₁ ( z ₁ ) удовлетворяет условию λ ⩽ Re w ₁ ⩽ µ, т.е. эта полоса является фундаментальной областью для группы сдвигов Γ ₁ . Если | ш ₁ | ≥ 1, то w ₁ лежит в X , и результат доказан. В противном случае пусть z ₂ = R ₁ ( w ₁ ) и находят g ₂ Γ ₁ такой, что w ₂ = g ₂ ( z ₂ ) удовлетворяет условию λ ⩽ Re w ₂ ⩽ µ. Если | ш ₂ | ≥ 1, то результат доказан. Продолжая таким же образом, либо некоторое w _n удовлетворяет | ш _н | ≥ 1, и в этом случае результат доказан; или | ш _н | < 1 для всех n . Теперь, поскольку g _{n + 1} лежит в Γ ₁ и | ш _н | < 1,

$\operatorname {Im} g_{n+1}(z_{n+1})=\operatorname {Im} z_{n+1}=\operatorname {Im} {\frac {w_{n}}{|w_{n}|{}^{2}}}={\frac {\operatorname {Im} w_{n}}{|w_{n}|{}^{2}}}.$

В частности

$\operatorname {Im} w_{n+1}\geq \operatorname {Im} w_{n}$

и

${\frac {\operatorname {Im} w_{n+1}}{\operatorname {Im} w_{n}}}=|w_{n}|^{-2}\geq 1.$

Таким образом, из неравенства выше точки ( w _n ) лежат в компакте | г | ≤ 1, λ ≤ Re z ≤ µ и Im z ≥ Im w ₁ . Отсюда следует, что | ш _н | стремится к 1; в противном случае существовало бы r < 1 такое, что | ш _м | ≤ r для бесконечного числа m , и тогда последнее уравнение выше будет означать, что Im w _n стремится к бесконечности, противоречие.

Пусть w — предельная точка w _n , так что | ш | = 1. Таким образом, w лежит на дуге единичной окружности между u и v . Если w ≠ u , v , то R ₁ w _n будет лежать в X при достаточно большом n , вопреки предположению. Следовательно, w = u или v . при n достаточно большом wn _{Следовательно ,} лежит близко к u или v и, следовательно, должно лежать в одном из отражений треугольника относительно вершины u или v , поскольку они заполняют окрестности u и v . существует элемент g в Γ такой, что ( wn ) _{Таким образом ,} лежит в X. g Поскольку по построению w _n находится на Γ-орбите точки z ₁ , то на этой орбите существует точка, лежащая в X , что и требовалось.

Идеальные треугольники

Мозаика для идеального треугольника со всеми его вершинами на единичной окружности и всеми углами 0 может рассматриваться как частный случай мозаики для треугольника с одной вершиной и двумя теперь нулевыми углами π /3 и π /2. Действительно, идеальный треугольник состоит из шести копий треугольника с одной вершиной, полученного отражением меньшего треугольника вокруг вершины с углом π /3.

• 
  Тесселяция треугольника с углами 0, π /3 и π /2
• 
  Тесселяция для идеального треугольника
• 
  Рисование линии замощения идеальными треугольниками

D - гармоническое сопряжение C относительно A и B.

Отражение идеального треугольника в одной из его сторон.

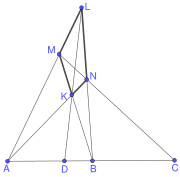
Однако каждый шаг мозаики однозначно определяется положением новых точек возврата на окружности или, что то же самое, на действительной оси; и эти моменты можно понять непосредственно с точки зрения серии Фари, следующей за Series (2015) , Hatcher (2013 , стр. 20–32) и Hardy & Wright (2008 , стр. 23–31). Все начинается с основного шага, который создает мозаику — отражение идеального треугольника на одной из его сторон. Отражение соответствует процессу инверсии в проективной геометрии и принятию проективно-гармонического сопряжения , которое можно определить через перекрестное отношение . Фактически, если p , q , r , s — разные точки в сфере Римана, то существует единственное комплексное преобразование Мёбиуса g, переводящее p , q и s в 0, ∞ и 1 соответственно. Перекрестное отношение ( p , q ; r , s ) определяется как g ( r ) и определяется по формуле

$(p,q;r,s)={\frac {(p-r)(q-s)}{(p-s)(q-r)}}.$

По определению он инвариантен относительно преобразований Мёбиуса. Если a , b лежат на вещественной оси, гармоническое сопряжение c относительно a и b определяется как уникальное действительное число d такое, что ( a , b ; c , d ) = −1. Так, например, если a = 1 и b = –1, сопряженное число r равно 1/ r . В общем, инвариантность Мёбиуса можно использовать для получения явной формулы для d через a , b и c . Действительно, переводя центр t = ( a + b )/2 круга с диаметром, имеющим конечные точки a и b, в 0, d – t является гармонически сопряженным c – t относительно a – t и b – t . Радиус круга равен ρ = ( b – a )/2, поэтому ( d – t )/ρ является гармоническим сопряжением ( c – t )/ρ относительно 1 и -1. Таким образом

${\frac {d-t}{\rho }}={\frac {\rho }{c-t}}$

так что

$d={\frac {\rho ^{2}}{r-t}}+t={\frac {(c-a)b+(c-b)a}{(c-a)+(c-b)}}.$

Теперь будет показано, что существует параметризация таких идеальных треугольников, заданная рациональными числами в сокращенной форме.

$a={\frac {p_{1}}{q_{1}}},\ b={\frac {p_{1}+p_{2}}{q_{1}+q_{2}}},\ c={\frac {p_{2}}{q_{2}}}$

где a и c удовлетворяют «условию соседства» p ₂ q ₁ − q ₂ p ₁ = 1.

Средний член b называется суммой Фарея или медианой внешних членов и записывается

$b=a\oplus c.$

Формула отраженного треугольника дает

$d={\frac {p_{1}+2p_{2}}{q_{1}+2q_{2}}}=a\oplus b.$

Аналогично отраженный треугольник во втором полукруге дает новую вершину b ⊕ c . Непосредственно проверяется, что a и b удовлетворяют условию соседства, как и b и c .

Теперь эту процедуру можно использовать для отслеживания треугольников, полученных последовательным отражением базового треугольника Δ с вершинами 0, 1 и ∞. Достаточно рассмотреть полосу с 0 ≤ Re z ≤ 1, поскольку та же картина воспроизводится в параллельных полосках применением отражений в линиях Re z = 0 и 1. Идеальный треугольник с вершинами 0, 1, ∞ отражает в полукруге с основанием [0,1] в треугольник с вершинами a = 0, b = 1/2, c = 1. Таким образом, a = 0/1 и c = 1/1 являются соседями и b = a ⊕ c . Полукруг разделен на два меньших полукруга с основаниями [ a , b ] и [ b , c ]. Каждый из этих интервалов разделяется на два интервала одним и тем же процессом, в результате чего получается 4 интервала. Продолжая таким же образом, мы получаем подразделения на 8, 16, 32 интервала и так далее. На n -м этапе имеется 2 ^н соседние интервалы с 2 ^н + 1 конечная точка. Приведенная выше конструкция показывает, что последовательные конечные точки удовлетворяют условию соседства, так что новые конечные точки, возникающие в результате отражения, задаются формулой суммы Фарея.

Чтобы доказать, что мозаика покрывает всю гиперболическую плоскость, достаточно показать, что каждое рациональное число в [0,1] в конечном итоге встречается в качестве конечной точки. Есть несколько способов увидеть это. Один из наиболее элементарных методов описан в Graham, Knuth & Patashnik (1994) при развитии — без использования цепных дробей — теории дерева Штерна-Броко , которая кодифицирует новые рациональные конечные точки, появляющиеся на n -м уровне. этап. Они дают прямое доказательство существования всякого рационального. Действительно, начиная с {0/1,1/1}, последовательные конечные точки вводятся на уровне n +1 путем добавления сумм Фарея или медиан ( p + r )/( q + s ) между всеми последовательными членами p / q , r / s на n -м уровне (как описано выше). Пусть x = a / b — рациональное число, лежащее между 0 и 1, причем a и b взаимно простые. Предположим, что на некотором уровне x зажат между последовательными членами p / q < x < r / s . Эти неравенства вынуждают aq – bp ≥ 1 и br – as ≥ 1 и, следовательно, поскольку rp – qs = 1 ,

$a+b=(r+s)(ap-bq)+(p+q)(br-as)\geq p+q+r+s.$

Это накладывает верхнюю границу на сумму числителей и знаменателей. С другой стороны, медиана ( p + r )/( q + s ) может быть введена и либо равна x , и в этом случае рациональный x появляется на этом уровне; или медиата дает новый интервал, содержащий x со строго большей суммой числителя и знаменателя. Таким образом, процесс должен завершиться не более чем через a + b шагов, тем самым доказывая, что x появляется.

Второй подход основан на модулярной группе G = SL(2, Z ). Алгоритм Евклида предполагает, что эта группа порождается матрицами

$S={\begin{pmatrix}0&1\\-1&0\end{pmatrix}},\,\,\,T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}.$

Фактически, пусть H будет подгруппой G, порожденной S и T . Позволять

$g={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$

быть элементом SL(2, Z ). Таким образом, ad − cb = 1, так что a и c взаимно просты. Позволять

$v={\begin{pmatrix}a\\c\end{pmatrix}},\,\,\,u={\begin{pmatrix}1\\0\end{pmatrix}}.$

Применяя при необходимости S , можно считать, что | а | > | с |(равенство невозможно в силу взаимной простоты). Пишем a = mc + r с0 ≤ р ≤ | с |. Но тогда

$T^{-m}{\begin{pmatrix}a\\c\end{pmatrix}}={\begin{pmatrix}r\\c\end{pmatrix}}.$

Этот процесс можно продолжать до тех пор, пока одна из записей не станет равна 0, и в этом случае другая обязательно будет равна ±1. Применяя при необходимости степень S , отсюда следует, что v = h u для некоторого h из H . Следовательно

$h^{-1}g={\begin{pmatrix}1&p\\0&q\end{pmatrix}}$

с целыми числами p , q . Очевидно, p = 1, так что h ⁻¹ г = Т ^д . Таким образом, g = h T ^д лежит в H, как и требовалось.

Чтобы доказать, что все рациональные числа в [0,1] встречаются, достаточно показать, что G переносит ∆ на треугольники в мозаике. Это следует из того, что сначала отметим, что S и T переносят ∆ в такой треугольник: действительно, как и преобразования Мёбиуса, S ( z ) = –1/ z и T ( z ) = z + 1, поэтому они дают отражения ∆ в двух из его стороны. Но тогда S и T сопрягают отражения в сторонах Δ с отражениями в сторонах S Δ и T Δ, лежащих в Γ. Таким образом, G нормализует Γ. Поскольку треугольники в мозаике - это в точности треугольники формы g ∆ с g в Γ, отсюда следует, что S и T и, следовательно, все элементы G переставляют треугольники в мозаике. Поскольку каждое рациональное число имеет форму g (0) для g в G , каждое рациональное число в [0,1] является вершиной треугольника в мозаике.

Группу отражений и мозаику для идеального треугольника также можно рассматривать как предельный случай группы Шоттки для трех непересекающихся невложенных кругов на сфере Римана. И снова эта группа порождается гиперболическими отражениями в трех кругах. В обоих случаях три окружности имеют общую окружность, которая пересекает их перпендикулярно. Используя преобразование Мёбиуса, можно предположить, что это единичная окружность или, что то же самое, действительная ось в верхней полуплоскости.

Подход Сигела

подход Карла Людвига Зигеля В этом подразделе изложен к теореме мозаики для треугольников. Менее элементарный подход Зигеля не использует выпуклость, вместо этого полагаясь на теорию римановых поверхностей , накрывающих пространств и версию теоремы монодромии для накрытий. Он был обобщен для доказательства более общей теоремы Пуанкаре о многоугольниках. (Обратите внимание, что частный случай замощения правильными n -угольниками с внутренними углами 2 π / n является непосредственным следствием мозаики треугольниками Шварца с углами π / n , π / n и π /2.)

Пусть Γ — свободное произведение Z ₂ ∗ Z ₂ ∗ Z ₂ . Если Δ = ABC — треугольник Шварца с углами π / a , π / b и π / c , где a , b , c ≥ 2, то существует естественное отображение Γ на группу, порожденное отражениями в сторонах Δ. . Элементы Γ описываются произведением трех генераторов, где никакие два соседних генератора не равны. В вершинах A , B и C произведение отражений от сторон, встречающихся в вершине, определяют повороты на углы 2 π / a , 2 π / b и 2 π / c ; Пусть g _A , g _B и g _C — соответствующие произведения образующих Γ = Z ₂ ∗ Z ₂ ∗ Z ₂ . Пусть Г0 _— нормальная подгруппа индекса 2 группы Г, состоящая из элементов, являющихся произведением четного числа образующих; и пусть Γ ₁ — нормальная подгруппа Γ, порожденная ( g _A ) ^а , ( г _Б ) ^б и ( г _С ) ^с . Они действуют на D тривиально. Пусть Γ = Γ/Γ ₁ и Γ ₀ = Γ ₀ /Γ ₁ .

Дизъюнктное объединение копий Δ, индексированных элементами из Γ с отождествлениями ребер, имеет естественную структуру римановой поверхности Σ. Во внутренней точке треугольника находится очевидная диаграмма. В качестве точки внутренней части ребра диаграмма получается путем отражения треугольника через ребро. В вершине треугольника с внутренним углом π / n карта получается из 2 n копий треугольника, полученных путем его последовательного отражения вокруг этой вершины. Группа Γ действует посредством преобразований колоды Σ, при этом элементы из Γ ₀ действуют как голоморфные отображения, а элементы, не входящие в Γ _0, действуют как антиголоморфные отображения.

Существует естественное отображение P точки Σ в гиперболическую плоскость. Внутренность треугольника с меткой g в Γ переносится на g (Δ), ребра переходят на ребра, а вершины на вершины. Также легко проверить, что окрестность внутренней точки ребра берется в окрестность изображения; и аналогично для вершин. Таким образом, P является локально гомеоморфизмом и поэтому переводит открытые множества в открытые множества. Таким образом, образ P (Σ), т. е. объединение трансляций g ( Δ ), является открытым подмножеством верхней полуплоскости. С другой стороны, это множество также закрыто. Действительно, если точка находится достаточно близко к Δ, она должна находиться в сдвиге Δ . Действительно, окрестность каждой вершины заполнена отражениями Δ , и если точка лежит вне этих трех окрестностей, но все еще близка к Δ, она должна лежать на трех отражениях Δ в ее сторонах. Таким образом, существует δ > 0 такое, что если z находится на расстоянии меньшем, чем δ, от Δ , то z лежит в Γ -переносе Δ . Поскольку гиперболическое расстояние Γ -инвариантно, отсюда следует, что если z находится на расстоянии меньшем, чем δ, от Γ( Δ ), на самом деле он лежит в Γ( Δ ), поэтому это объединение замкнуто. Из связности следует, что P (Σ) — вся верхняя полуплоскость.

С другой стороны, P — локальный гомеоморфизм, то есть накрывающее отображение. Поскольку верхняя полуплоскость односвязна, отсюда следует, что P одноединичный и, следовательно, сдвиги Δ замощают верхнюю полуплоскость. Это является следствием следующей версии теоремы о монодромии для покрытий римановых поверхностей: если Q — отображение покрытия между римановыми поверхностями 1 _и 2 _, то любой путь из ₂ можно поднять до пути в ₁ и любой два гомотопических пути с одинаковыми концами поднимаются до гомотопических путей с одинаковыми конечными точками; непосредственным следствием является то, что если ₂ односвязно, то Q должен быть гомеоморфизмом. Чтобы применить это, пусть Σ ₁ = Σ, пусть Σ ₂ — верхняя полуплоскость и пусть Q = P . По следствию теоремы монодромии P должно быть однозначно.

Отсюда также следует, что g (∆) = ∆ тогда и только тогда, когда g лежит в Γ ₁ , так что гомоморфизм Γ ₀ в группу Мёбиуса является точным.

Группы гиперболического отражения

См. Также: Равномерные мозаики в гиперболической плоскости.

Мозаику треугольников Шварца можно рассматривать как обобщение теории бесконечных групп Кокстера , следуя теории гиперболических групп отражений , алгебраически развитой Жаком Титсом. и геометрически Эрнестом Винбергом . В случае с Лобачевским или гиперболической плоскостью идеи берут начало в работах Анри Пуанкаре и Вальтера фон Дейка девятнадцатого века . Однако, как Джозеф Ленер отметил в «Математических обзорах» , строгие доказательства того, что отражения треугольника Шварца порождают мозаику, часто были неполными, одним из примеров является его собственная книга 1964 года «Разрывные группы и автоморфные функции» . Строгими доказательствами являются элементарная трактовка Каратеодори в его учебнике Funktiontheorie 1950 года , переведенном на английский язык в 1954 году, и отчет Сигела 1954 года, использующий принцип монодромии. Здесь будет обобщен подход с использованием групп Кокстера в общих рамках классификации групп гиперболического отражения.

Пусть r, s, t — символы и пусть a , b , c ≥ 2 — целые числа, возможно, ∞ , причем

$${1 \over a}+{1 \over b}+{1 \over c}<1.$$

Определим Γ как группу с представлением, имеющим генераторы r, s, t, которые все являются инволюциями и удовлетворяют условиям $${\begin{aligned}(st)^{a}&=1,\\[2pt](tr)^{b}&=1,\\[2pt](rs)^{c}&=1.\end{aligned}}$$Если одно из целых чисел бесконечно, то произведение имеет бесконечный порядок. Генераторы r, s, t называются простыми отражениями .

Набор $${\begin{aligned}A&={\begin{cases}\cos {\frac {\pi }{a}}&{\text{if }}a\geq 2{\text{ is finite,}}\\[2pt]\cosh x,\ x>0&{\text{otherwise.}}\end{cases}}\\[8pt]B&={\begin{cases}\cos {\frac {\pi }{b}}&{\text{if }}b\geq 2{\text{ is finite,}}\\[2pt]\cosh y,\ y>0&{\text{otherwise.}}\end{cases}}\\[8pt]C&={\begin{cases}\cos {\frac {\pi }{c}}&{\text{if }}c\geq 2{\text{ is finite,}}\\[2pt]\cosh z,\ z>0&{\text{otherwise.}}\end{cases}}\end{aligned}}$$Пусть e _r , es _с , e _t — базис трехмерного вещественного векторного пространства V симметричной билинейной формой Λ такой, что $${\begin{aligned}\Lambda (\mathbf {e} _{s},\mathbf {e} _{t})&=-A,\\[2pt]\Lambda (\mathbf {e} _{t},\mathbf {e} _{r})&=-B,\\[2pt]\Lambda (\mathbf {e} _{r},\mathbf {e} _{s})&=-C,\end{aligned}}$$с тремя диагональными элементами, равными одному. Симметричная билинейная форма Λ невырождена с сигнатурой (2, 1) . Определять: $${\begin{aligned}\rho (\mathbf {v} )&=\mathbf {v} -2\Lambda (\mathbf {v} ,\mathbf {e} _{r})\mathbf {e} _{r}\\[2pt]\sigma (\mathbf {v} )&=\mathbf {v} -2\Lambda (\mathbf {v} ,\mathbf {e} _{s})\mathbf {e} _{s}\\[2pt]\tau (\mathbf {v} )&=\mathbf {v} -2\Lambda (\mathbf {v} ,\mathbf {e} _{t})\mathbf {e} _{t}\end{aligned}}$$

Теорема (геометрическое представление). Операторы , τ являются инволюциями на V ρ, σ с соответствующими собственными векторами e _r , e _s , e _t с простым собственным значением −1. Произведения операторов имеют порядок, соответствующий приведенному выше представлению (поэтому στ имеет порядок и a т. д.). Операторы ρ, σ, τ индуцируют представление Γ на V , сохраняющее Λ .

Билинейная форма Λ базиса имеет матрицу

$$M={\begin{pmatrix}1&-C&-B\\-C&1&-A\\-B&-A&1\\\end{pmatrix}},$$

так же имеет определитель $$\det(M)=1-A^{2}-B^{2}-C^{2}-2ABC.$$ Если , скажем, c = 2 , то собственные значения матрицы равны $1,\ 1\pm {\sqrt {A^{2}+B^{2}}}.$ Состояние ${\tfrac {1}{a}}+{\tfrac {1}{b}}<{\tfrac {1}{2}}$ немедленно заставляет $A^{2}+B^{2}>1,$ так что Λ должен иметь сигнатуру (2, 1) . Итак, в общем случае a , b , c ≥ 3 . Очевидно, что случай, когда все равны 3, невозможен. Но тогда определитель матрицы отрицателен, а ее след положителен. В результате два собственных значения положительны, а одно отрицательно, т.е. Λ имеет сигнатуру (2, 1) . Очевидно , ρ, σ, τ являются инволюциями, сохраняющими Λ с заданными −1 собственными векторами.

Чтобы проверить порядок произведений типа στ , достаточно отметить, что:

1. отражения σ и τ порождают конечную или бесконечную группу диэдра ;
2. двумерная линейная оболочка U es e _; и t _τ инвариантна относительно σ и с ограничением Λ положительно определенным
3. W , ортогональное дополнение к U , отрицательно определено на Λ , а и τ действуют тривиально на W. σ

(1) понятно, поскольку если γ = στ порождает нормальную подгруппу с σγσ ⁻¹ = с ⁻¹ . Для (2) U инвариантен по определению, а матрица положительно определена, поскольку $0<\cos {\tfrac {\pi }{a}}<1.$ Поскольку Λ имеет сигнатуру (2, 1) , ненулевой вектор w в W должен удовлетворять Λ( w , w ) < 0 . По определению, σ имеет собственные значения 1 и –1 на U , поэтому w должно быть зафиксировано σ . Аналогично w должно быть зафиксировано τ , чтобы (3) было доказано. Наконец в (1)

$${\begin{alignedat}{5}\sigma (\mathbf {e} _{s})&=-{\mathbf {e} }_{s},&\quad \tau (\mathbf {e} _{s})&=2\cos({\tfrac {\pi }{a}})\,\mathbf {e} _{s}+\mathbf {e} _{t},\\[2pt]\sigma (\mathbf {e} _{t})&=2\cos({\tfrac {\pi }{a}})\,\mathbf {e} _{s}+\mathbf {e} _{t},&\quad \tau (\mathbf {e} _{t})&=-{\mathbf {e} }_{t},\end{alignedat}}$$

так что, если a конечно, собственные значения στ равны -1, ς и ς ⁻¹ , где $\varsigma =e^{\frac {2\pi i}{a}};$ и если a бесконечно, собственные значения равны -1, X и X ⁻¹ , где $X=e^{2x}.$ Более того, простой индукционный аргумент показывает, что если $\theta ={\tfrac {\pi }{a}}$ затем

$${\begin{aligned}(\sigma \tau )^{m}({\mathbf {e} }_{s})&=\left[{\frac {\sin(2m+1)\theta }{\sin \theta }}\right]{\mathbf {e} }_{s}+\left[{\frac {\sin 2m\theta }{\sin \theta }}\right]{\mathbf {e} }_{t},\\[4pt]\tau (\sigma \tau )^{m}({\mathbf {e} }_{s})&=\left[{\frac {\sin(2m+1)\theta }{\sin \theta }}\right]{\mathbf {e} }_{s}+\left[{\frac {\sin(2m+2)\theta }{\sin \theta }}\right]{\mathbf {e} }_{t},\end{aligned}}$$

и если х > 0, то

$${\begin{aligned}(\sigma \tau )^{m}({\mathbf {e} }_{s})&=\left[{\frac {\sinh(2m+1)x}{\sinh x}}\right]{\mathbf {e} }_{s}+\left[{\frac {\sinh 2mx}{\sinh x}}\right]{\mathbf {e} }_{t},\\[4pt]\lim _{x\to 0}\ (\sigma \tau )^{m}(\mathbf {e} _{s})&=(2m+1)\mathbf {e} _{s}+2m\mathbf {e} _{t};\\[12pt]\tau (\sigma \tau )^{m}({\mathbf {e} }_{s})&=\left[{\frac {\sinh(2m+1)x}{\sinh x}}\right]{\mathbf {e} }_{s}+\left[{\frac {\sinh(2m+2)x}{\sinh x}}\right]{\mathbf {e} }_{t},\\[4pt]\lim _{x\to 0}\,\tau (\sigma \tau )^{m}(\mathbf {e} _{s})&=(2m+1)\mathbf {e} _{s}+(2m+2)\mathbf {e} _{t}.\end{aligned}}$$

Пусть Γ _a — подгруппа диэдра в Γ, порожденная s и t , с аналогичными определениями для Γ _b и Γ _c . Аналогично определите Γ _r как циклическую подгруппу Γ, заданную 2-группой {1, r }, с аналогичными определениями для Γ _s и Γ _t . По свойствам геометрического представления все шесть этих групп точно действуют на V . В частности Γ _a можно отождествить с группой, порожденной σ и τ ; как и выше, оно явно разлагается в прямую сумму двумерного неприводимого подпространства U и одномерного подпространства W с тривиальным действием. Таким образом, существует единственный вектор $$\mathbf {w} =\mathbf {e} _{r}+\lambda \mathbf {e} _{s}+\mu \mathbf {e} _{t}$$в W, удовлетворяющем σ ( w ) = w и τ ( w ) = w . Явно, $$\lambda ={\frac {C+AB}{1-A^{2}}},\quad \mu ={\frac {B+AC}{1-A^{2}}}.$$

Замечание о представлениях групп диэдра. Хорошо известно, что для конечномерных вещественных пространств со скалярными произведениями две ортогональные инволюции S и T могут быть разложены как ортогональная прямая сумма двумерных или одномерных инвариантных пространств; например, это можно вывести из наблюдения Пола Халмоша и других, что положительный самосопряженный оператор ( S – T ) ² коммутирует как с S, так и с T . Однако в приведенном выше случае, когда билинейная форма Λ больше не является положительно определенным скалярным произведением, другие специальные необходимо привести рассуждения.

Теорема (Титса). Геометрическое представление группы Кокстера точное.

Этот результат был впервые доказан Титсом в начале 1960-х годов и впервые опубликован в тексте Бурбаки (1968) с его многочисленными упражнениями. В тексте фундаментальная палата была введена индуктивным аргументом; Упражнение 8 в §4 главы V было расширено Винаем Деодхаром для разработки теории положительных и отрицательных корней и, таким образом, сокращения исходного аргумента Титса.

Пусть X — выпуклый конус сумм κ e _r + λ e _s + µ e _t с вещественными неотрицательными коэффициентами, не все из которых равны нулю. Для g в группе Γ определим ℓ( g ) , длина слова или length , чтобы быть минимальным количеством отражений от r, s, t, необходимых для записи g как упорядоченной композиции простых отражений. Определим положительный корень как вектор g e _r , g e _s или g e _{r ,} лежащий в X , с g в Γ .

Обычно по определениям проверяют, что

• если | ℓ( гк ) – ℓ( г ) | = 1 для простого отражения q и, если g ≠ 1 , всегда существует простое отражение q такое, что ℓ( g ) = ℓ( gq ) + 1 ;
• для g и h в Γ , ℓ( gh ) ≤ ℓ( g ) + ℓ( h ) .

Предложение. Если g находится в Γ и ℓ( gq ) = ℓ( g ) ± 1 для простого отражения q , то g e _q лежит в ± X и , следовательно, является положительным или отрицательным корнем в зависимости от знака.

При замене g на gq необходимо учитывать только положительный знак. Утверждение будет доказано индукцией по ℓ( g ) = m , оно тривиально при m = 0 .Предположим, что ℓ( gs ) = ℓ( g ) + 1 . Если ℓ( g ) = m > 0 , без ограничения общности можно предположить, что минимальное выражение для g заканчивается на ...t . Поскольку s и t порождают группу диэдра Γ _a , g можно записать как произведение g = hk , где k = ( st ) ^н или т ( ст ) ^н и h имеет минимальное выражение, которое заканчивается на ...r , но никогда на s или t . Это означает, что ℓ( hs ) = ℓ( h ) + 1 и ℓ( ht ) = ℓ( h ) + 1 . Поскольку ℓ( h ) < m , предположение индукции показывает, что оба h e _s , h e _t лежат в X . Поэтому достаточно показать, что k e _s имеет вид λ e _s + µ e _t с λ , µ ≥ 0 , а не оба 0. Но это уже проверено в формулах выше.

Следствие (доказательство теоремы Титса). Геометрическое представление верно.

Достаточно показать, что если фиксирует er , _es то , _e g t _, g = 1 . Учитывая минимальное выражение для g ≠ 1 , условия ℓ( gq ) = ℓ( g ) + 1 явно не могут быть одновременно удовлетворены тремя простыми отражениями q .

Обратите внимание, что, как следствие теоремы Титса, генераторы (слева) удовлетворяют условиям (справа): $${\begin{alignedat}{5}(g&=st)\ \ {\text{ s.t. }}&g^{a}=1,\\[4pt](h&=tr)\ \ {\text{ s.t. }}&h^{b}=1,\\[4pt](k&=rs)\ \ {\text{ s.t. }}&k^{c}=1,\\[4pt]&&ghk=1.\end{alignedat}}$$Это дает представление о сохраняющей ориентацию нормальной подгруппе индекса 2 Γ ₁ группы Γ . Представление соответствует фундаментальной области, полученной путем отражения двух сторон геодезического треугольника с образованием геодезического параллелограмма (частный случай теоремы Пуанкаре о многоугольнике).

Дальнейшие последствия. Корни представляют собой непересекающееся объединение положительных и отрицательных корней. Простое отражение q переставляет каждый положительный корень, кроме e _q . Для g в Γ благодаря ℓ( g ) — это количество положительных корней, ставших отрицательными g .

Фундаментальная область и конус Титса.

Пусть G — трехмерная замкнутая подгруппа Ли группы GL( V ), сохраняющая Λ . Поскольку V можно отождествить с трехмерным пространством Лоренца или Минковского с сигнатурой (2,1) , группа G изоморфна группе Лоренца O(2,1) и, следовательно, $\mathrm {SL} _{\pm }(2,\mathbb {R} )\setminus \{\pm \,I\,\}.$ Выбирая e в качестве положительного корневого вектора в X , стабилизатор e представляет собой максимальную компактную подгруппу K группы G, изоморфную O(2) . Однородное пространство X = G / K — симметричное пространство постоянной отрицательной кривизны, которое можно отождествить с двумерным гиперболоидом или плоскостью Лобачевского. ${\mathfrak {H}}^{2}$. Дискретная группа Γ действует разрывно на G / K : фактор-пространство Γ \ G / K компактно, если все a, b, c конечны, и имеют конечную площадь в противном случае. Результаты о фундаментальной камере Титса имеют естественную интерпретацию в терминах соответствующего треугольника Шварца, что непосредственно переводится в свойства мозаики геодезического треугольника через гиперболическую группу отражений Γ . Переход от групп Кокстера к мозаике впервые можно найти в упражнениях §4 главы V Бурбаки (1968) , принадлежащих Титсу, и у Ивахори (1966) ; в настоящее время доступно множество других эквивалентных методов лечения, не всегда непосредственно сформулированных в терминах симметричных пространств.

Подход Маскита, де Рама и Бердона

Маскит (1971) дал общее доказательство теоремы Пуанкаре о многоугольниках в гиперболическом пространстве; аналогичное доказательство было дано в работе де Рама (1971) . Специализируясь на гиперболической плоскости и треугольниках Шварца, это можно использовать для создания современного подхода к установлению существования мозаики треугольников Шварца, как описано в Бердоне (1983) и Маските (1988) . Швейцарские математики де ла Гарп (1991) и Хефлигер представили вводный отчет, взяв геометрическую теорию групп . за отправную точку

См. также

• Список однородных многогранников по треугольнику Шварца
• Символ Витхоффа
• Строительство Витхоффа
• Однородный многогранник
• Невыпуклый однородный многогранник
• Плотность (многогранник)
• Тетраэдр Гурса
• Регулярная гиперболическая мозаика
• Равномерные мозаики в гиперболической плоскости

Ссылки

• Коксетер, HSM (1973), Правильные многогранники (Третье изд.), Dover Publications, ISBN  0-486-61480-8 , Таблица 3: Треугольники Шварца
• Шварц, Х.А. (1873), «О тех случаях, когда гипергеометрический ряд Гаусса представляет собой алгебраическую функцию своего четвертого элемента» , Журнал чистой и прикладной математики , 1873 (75): 292–335, doi : 10.1515/crll.1873.75 .292 , ISSN   0075-4102 , S2CID   121698536 (Обратите внимание, что Коксетер ссылается на это как на «К теории гипергеометрического ряда», это краткое название, используемое в заголовках страниц журнала).
• Веннингер, Магнус Дж. (1979), «Введение в понятие многогранной плотности», Сферические модели , Архив CUP, стр. 132–134 , ISBN  978-0-521-22279-2

• Абраменко, Петр; Браун, Кеннет С. (2007). Здания: теория и приложения . Тексты для аспирантов по математике. Том. 248. Шпрингер-Верлаг . ISBN  978-0-387-78834-0 . МР   2439729 .
• Бердон, Алан Ф. (1983), «Теорема Пуанкаре», Геометрия дискретных групп , Тексты для аспирантов по математике, том. 91, Спрингер, стр. 242–252, ISBN.  0-387-90788-2
• Бердон, Алан Ф. (1984), «Букварь по римановым поверхностям» , Серия лекций Лондонского математического общества , 78 , Cambridge University Press, ISBN  0521271045
• Бергер, Марсель (2010), Раскрытая геометрия. Лестница Иакова к современной высшей геометрии , перевод Лестера Сенешала, Springer, ISBN  978-3-540-70996-1
• Берндт, Брюс С .; Кнопп, Марвин И. (2008), Теория модулярных форм Гекке и ряды Дирихле , Монографии по теории чисел, том. 5, Всемирный научный, ISBN  978-981-270-635-5
• Бурбаки, Николя (1968). «Глава IV: Группы Кокстера и системы Титса • Глава V: Группы, порожденные отражениями». Группы и алгебры Ли . Элементы математики (на французском языке). Париж: Германн. стр. 1–56, 57–141. МР   0240238 . Перепечатано Массоном в 1981 году как ISBN   2-225-76076-4 .
• Бридсон, Мартин Р .; Хефлигер, Андре (1999). «I. Основной материал по SL ₂ (R), дискретным подгруппам и верхней полуплоскости». Метрические пространства неположительной кривизны (PDF) . Основные принципы математических наук. Том 319. Шпрингер-Верлаг . ISBN  3-540-64324-9 . МР   1744486 .
• Браун, Кеннет С. (1989). Здания . Спрингер-Верлаг . ISBN  0-387-96876-8 . МР   0969123 .
• Каратеодори, Константин (1954), Теория функций комплексной переменной , вып. 2, перевод Ф. Стейнхардта, Челси
• Дэвис, Майкл В. (2008), «Приложение D. Геометрическое представление», Геометрия и топология групп Кокстера , Монографии Лондонского математического общества, том. 32, Princeton University Press , стр. 439–447, ISBN.  978-0-691-13138-2
• де ла Арп, Пьер (1991). «Приглашение в группы Кокстера». Теория групп с геометрической точки зрения (Триест, 1990) . Всемирная научная . стр. 193–253. МР   1170367 .
• Деодхар, Винай В. (1982). «О корневой системе группы Кокстера». Комм. Алгебра . 10 (6): 611–630. дои : 10.1080/00927878208822738 . МР   0647210 .
• Деодхар, Винай В. (1986). «Некоторые характеристики групп Кокстера» . Энсен. Математика. 32 : 111–120. МР   0850554 .
• де Рам, Г. (1971). «О многоугольниках, порождающих фуксовы группы» . Учите. Математика. (на французском языке). 17 :49–61.
• Эллис, Грэм (2019). «Треугольные группы». Приглашение к вычислительной гомотопии . Издательство Оксфордского университета . стр. 441–444. ISBN  978-0-19-883298-0 . МР   3971587 .
• Эпштейн, Дэвид Б.А .; Петронио, Карло (1994). «Изложение теоремы Пуанкаре о многограннике» . Энсен. Математика. 40 : 113–170. МР   1279064 .
• Эванс, Рональд (1973), «Фундаментальная область модульной группы Хекке», Journal of Number Theory , 5 (2): 108–115, Бибкод : 1973JNT.....5..108E , doi : 10.1016/0022- 314x(73)90063-2
• Фрике, Роберт ; Кляйн, Феликс (1897), Лекции по теории автоморфных функций. Первый том; Основы теории групп (на немецком языке), Б. Г. Тойбнер, ISBN  978-1-4297-0551-6 , ЯФМ   28.0334.01
• Грэм, Рональд Л .; Кнут, Дональд Э .; Паташник, Орен (1994), Конкретная математика (2-е изд.), Аддисон-Уэсли, стр. 116–118, ISBN  0-201-55802-5
• Харди, штат Джорджия ; Райт, Э.М. (2008), Введение в теорию чисел (6-е изд.), Oxford University Press, ISBN  978-0-19-921986-5
• Хэтчер, Аллен (2013). «1. Диаграмма Фарея». Топология чисел (PDF) . Корнеллский университет . Проверено 25 февраля 2022 г.
• Хекке, Э. (1935), «Об определении рядов Дирихле их функциональным уравнением», Mathematical Annals (на немецком языке), 112 : 664–699, doi : 10.1007/bf01565437
• Хекман, Герт Дж. (2018). «Группы Кокстера» (PDF) . Университет Радбауд в Неймегене . Проверено 3 марта 2022 г.
• Хиллер, Ховард (1982). Геометрия групп Кокстера . Исследования по математике. Том. 54. Питман. ISBN  0-273-08517-4 . МР   0649068 .
• Хоулетт, Роберт (1996). «Введение в группы Кокстера» . Семинар по теории геометрических групп Австралийского национального университета . Сидней . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Хамфрис, Джеймс Э. (1990). Группы отражения и группы Кокстера . Кембриджские исследования по высшей математике. Том. 29. Издательство Кембриджского университета . ISBN  0-521-37510-Х . МР   1066460 .
• Иверсен, Биргер (1992), Гиперболическая геометрия , Студенческие тексты Лондонского математического общества, том. 25, Издательство Кембриджского университета, ISBN  0-521-43508-0
• Ивахори, Нагаёси (1966). «О дискретных группах отражений на симметричных римановых многообразиях». Учеб. Американо-японский семинар по дифференциальной геометрии (Киото, 1965 г.) . Токио: Ниппон Хёронша. стр. 57–62. МР   0217741 .
• Ленер, Джозеф (1964), Разрывные группы и автоморфные функции , Математические обзоры, том. 8, Провиденс, Род-Айленд: Американское математическое общество, MR   0164033
• Магнус, Вильгельм (1974), Неевклидовы мозаики и их группы , Чистая и прикладная математика, том. 61, Академик Пресс
• Магнус, Вильгельм ; Каррасс, Авраам; Солитар, Дональд (1976). Комбинаторная теория групп: представления групп через генераторы и отношения (второе исправленное изд.). Дуврские книги . МР   0207802 .
• Маскит, Бернар (1971), «О теореме Пуанкаре для фундаментальных многоугольников», Успехи в математике , 7 (3): 219–230, doi : 10.1016/s0001-8708(71)80003-8
• Маскит, Бернард (1988). «Теорема Пуанкаре». Клейновы группы . Основные принципы математических наук. Том 287. Шпрингер-Верлаг . ISBN  3-540-17746-9 . МР   0959135 .
• Максвелл, Джордж (1982). «Сферические упаковки и гиперболические группы отражений» . Дж. Алгебра . 79 : 78–97. дои : 10.1016/0021-8693(82)90318-0 . МР   0679972 .
• МакМаллен, Кертис Т. (1998), «Хаусдорфова размерность и конформная динамика. III. Вычисление размерности», American Journal of Mathematics , 120 : 691–721, doi : 10.1353/ajm.1998.0031 , S2CID   15928775
• Милнор, Джон (1975). «О трехмерных многообразиях Брискорна M(p,q,r)». Узлы, группы и трехмерные многообразия (Статьи, посвященные памяти Р. Х. Фокса) . Энн. математики. Исследования. Том. 84. Издательство Принстонского университета . стр. 175–225. МР   0418127 .
• Мамфорд, Дэвид ; Сериал, Кэролайн ; Райт, Дэвид (2015), Жемчуг Индры. Видение Феликса Кляйна , издательство Кембриджского университета, ISBN  978-1-107-56474-9
• Серия, Кэролайн (2015), Цепные дроби и гиперболическая геометрия, Летняя школа LMS Лафборо (PDF) , получено 15 февраля 2017 г.
• Сигел, CL (1971), Темы теории комплексных функций , вып. II. Автоморфные функции и абелевы интегралы в переводе А. Шеницера; М. Треткофф, Wiley-Interscience, стр. 85–87, ISBN.  0-471-60843-2
• Стейнберг, Роберт (1968). Эндоморфизмы линейных алгебраических групп . Мемуары Американского математического общества . Том. 80. Американское математическое общество . МР   0230728 .
• Такеучи, Кисао (1977a), «Группы арифметических треугольников», Журнал Математического общества Японии , 29 : 91–106, doi : 10.2969/jmsj/02910091
• Такеучи, Кисао (1977b), «Классы соизмеримости групп арифметических треугольников», Журнал факультета естественных наук Токийского университета, раздел IA, Математика , 24 : 201–212.
• Трелфолл, В. (1932), «Групповые картинки» (PDF) , Трактаты математическо-физического класса Саксонской академии наук , 41 , Хирцель: 1–59
• Титс, Жак (2013). «Группы и геометрии Кокстера». У Ф. Букенхаута; Б.М. Мюльхерр; ДжП. Тиньоль ; Х. Ван Мальдегем (ред.). Œuvres/Собрание сочинений, Том I. Наследие европейской математики (на французском языке). Цюрих: Европейское математическое общество . стр. 803–817. ISBN  978-3-03719-126-2 . Эта рукопись стала основополагающим текстом теории групп Кокстера, использованным для подготовки главы IV книги Бурбаки «Группы и алгебры лжи» ; Впервые он был опубликован в 2001 году.
• Винберг, Эрнест Б. (1971). «Дискретные линейные группы, порожденные отражениями». Математика СССР-Известия . 5 (5). Перевод П. Флора: 1083–1119. Бибкод : 1971ИзМат...5.1083В . дои : 10.1070/IM1971v005n05ABEH001203 . МР   0302779 .
• Винберг, Эрнест Б. (1985). «Гиперболические группы отражений» . Российские математические обзоры . 40 (1). Перевод Дж. Вигольда. Лондонское математическое общество : 31–75. Бибкод : 1985РуМаС..40...31В . doi : 10.1070/RM1985v040n01ABEH003527 . S2CID   250912767 .
• Винберг, Эрнест Б .; Шварцман О.В. (1993). «Дискретные группы движений пространств постоянной кривизны». Геометрия II: Пространства постоянной кривизны . Энциклопедия математики. наук. Том. 29. Шпрингер-Верлаг . стр. 139–248. ISBN  3-540-52000-7 . МР   1254933 .
• Вебер, Маттиас (2005), «Маленький звездчатый додекаэдр Кеплера как риманова поверхность» , Pacific Journal of Mathematics , 220 : 167–182, doi : 10.2140/pjm.2005.220.167

Внешние ссылки

• Вайсштейн, Эрик В. «Черный треугольник» . Математический мир .
• Клитцинг, Ричард. «3D Общий треугольник Шварца (pqr) и обобщенные матрицы инцидентности соответствующих многогранников» .