Усеченная шестиугольная плитка порядка 4
| Усеченная шестиугольная плитка порядка 4 | |
|---|---|
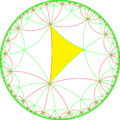
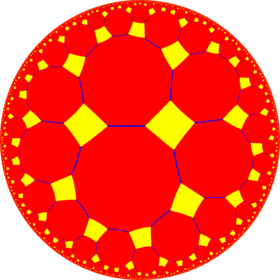 Модель диска Пуанкаре гиперболической плоскости | |
| Тип | Гиперболическая равномерная мозаика |
| Конфигурация вершин | 4.12.12 |
| Символ Шлефли | т{6,4} tr{6,6} или |
| Символ Витхоффа | 2 4 | 6 2 6 6 | |
| Диаграмма Кокстера | |
| Группа симметрии | [6,4], (*642) [6,6], (*662) |
| Двойной | Квадратная плитка тетракиса порядка 6 |
| Характеристики | Вершинно-транзитивный |
В геометрии усеченная шестиугольная мозаика четвертого порядка представляет собой равномерную мозаику гиперболической плоскости . Он имеет символ Шлефли t{6,4}. Вторичная конструкция tr{6,6} называется усечённой шестиугольной мозаикой с двумя цветами додекагонов .
Конструкции
[ редактировать ]Существуют две однородные конструкции этого мозаики, первая из [6,4] калейдоскоп , и более низкая симметрия за счет удаления последнего зеркала, [6,4,1 + ], дает [6,6], (*662).
| Имя | Тетрашестиугольный | Усеченный шестиугольный |
|---|---|---|
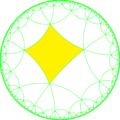
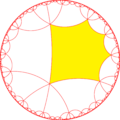
| Изображение |  |  |
| Симметрия | [6,4] (*642) | [6,6] = [6,4,1 + ] (*662) |
| Символ | т{6,4} | тр{6,6} |
| Диаграмма Кокстера |
Двойная черепица
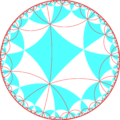
[ редактировать ] |  |
| Двойная мозаика, квадратная мозаика тетракиса 6-го порядка, имеет конфигурацию граней V4.12.12 и представляет собой фундаментальные области группы симметрии [6,6]. | |
Связанные многогранники и мозаика
[ редактировать ]| * n 42 мутация симметрии усеченных мозаик: 4,2 n .2 n |
|---|
| Однородные тетрагексагональные мозаики |
|---|
| Равномерные шестиугольные мозаики |
|---|
Симметрия
[ редактировать ]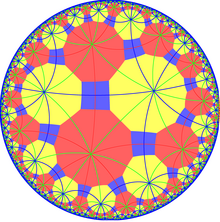
Двойственный тайлинг представляет фундаментальные области (*662) орбифолдной симметрии. Согласно симметрии [6,6] (*662), существует 15 малых индексных подгрупп (12 уникальных) с помощью операторов зеркального удаления и чередования . Зеркала можно удалить, если все его порядки ветвей четные, и это сокращает соседние порядки ветвей пополам. Удаление двух зеркал оставляет точку вращения половинного порядка, где встречаются удаленные зеркала. В этих изображениях фундаментальные области попеременно окрашены в черный и белый цвета, а на границах между цветами существуют зеркала. Индекс подгруппы -8 группа, [1 + ,6,1 + ,6,1 + ] (3333) — коммутатор из [6,6].
Большая подгруппа, построенная как [6,6 * ], удаляя точки вращения (6*3), индекс 12 становится (*333333).
Симметрию можно удвоить до симметрии 642 , добавив зеркало, чтобы разделить фундаментальную область пополам.
| Малые индексные подгруппы [6,6] (*662) |
|---|
Ссылки
[ редактировать ]- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
См. также
[ редактировать ]- Квадратная плитка
- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Гиперболическая мозаика» . Математический мир .
- Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре» . Математический мир .
- Галерея гиперболических и сферических плиток
- KaleidoTile 3: образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик.
- Гиперболические плоские мозаики, Дон Хэтч