Восьмиугольная плитка
Эта статья может быть слишком технической для понимания большинства читателей . ( Май 2021 г. ) |
| Восьмиугольная плитка | |
|---|---|
 Модель диска Пуанкаре гиперболической плоскости | |
| Тип | Гиперболическая регулярная мозаика |
| Конфигурация вершин | 8 3 |
| Символ Шлефли | {8,3} т{4,8} |
| Символ Витхоффа | 3 | 8 2 2 8 | 4 4 4 4 | |
| Диаграмма Кокстера | |
| Группа симметрии | [8,3], (*832) [8,4], (*842) [(4,4,4)], (*444) |
| Двойной | Треугольная плитка порядка 8 |
| Характеристики | Вершинно-транзитивный , реберно-транзитивный , грани-транзитивный |
В геометрии восьмиугольная мозаика — это правильная мозаика гиперболической плоскости . Он представлен Шлефли символом {8,3} , имеющим три правильных восьмиугольника вокруг каждой вершины. Он также имеет конструкцию в виде усеченной квадратной мозаики восьмого порядка, t{4,8}.
Равномерные раскраски
[ редактировать ]Как и шестиугольная мозаика евклидовой плоскости, эта гиперболическая мозаика имеет три однородные раскраски. Двойная мозаика V8.8.8 представляет фундаментальные области симметрии [(4,4,4)].
| Обычный | Усечения | ||
|---|---|---|---|
 {8,3} | 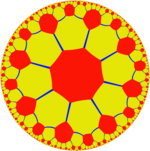 т{4,8} |  т{4 [3] } | |
| Двойная черепица | |||
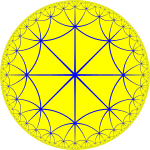 {3,8} |  |  | |
Обычные карты
[ редактировать ]Регулярное отображение {8,3} 2,0 можно рассматривать как 6-раскраску гиперболического мозаики {8,3}. На обычной карте восьмиугольники одного цвета считаются одной и той же гранью, показанной в нескольких местах. Нижние индексы 2,0 показывают, что один и тот же цвет будет повторяться при перемещении на 2 шага в прямом направлении по противоположным краям. Эта обычная карта также имеет представление в виде двойного покрытия куба, представленного символом Шлефли {8/2,3}, с 6 восьмиугольными гранями, двойной оберткой {8/2}, с 24 ребрами и 16 вершинами. Он был описан Бранко Грюнбаумом в его статье 2003 года « Являются ли ваши многогранники такими же, как мои многогранники?» [1]
Связанные многогранники и мозаики
[ редактировать ]Это замощение топологически является частью последовательности правильных многогранников и замощений с символом Шлефли {n,3}.
| * n 32 мутация симметрии правильных мозаик: { n ,3} |
|---|
А также топологически является частью последовательности правильных мозаик с символом Шлефли {8,n}.
| Космос | сферический | Компактный гиперболический | Паракомпакт | |||||
|---|---|---|---|---|---|---|---|---|
| Укладка плитки |  |  |  |  |  |  |  | |
| Конфиг. | 8.8 | 8 3 | 8 4 | 8 5 | 8 6 | 8 7 | 8 8 | ... 8 ∞ |
Из конструкции Витхоффа существует десять гиперболических однородных мозаик , которые могут быть основаны на правильной восьмиугольной мозаике.
Если нарисовать плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета по исходным краям, получится 10 форм.
| Однородные восьмиугольные/треугольные плитки |
|---|
| Однородные восьмиугольные/квадратные плитки |
|---|
| Равномерные (4,4,4) мозаики |
|---|
См. также
[ редактировать ]- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Ссылки
[ редактировать ]- ^ Грюнбаум, Бранко (2003). «Ваши многогранники такие же, как мои многогранники?» (PDF) . Дискретная и вычислительная геометрия . 25 : 461–488. дои : 10.1007/978-3-642-55566-4_21 . Проверено 27 апреля 2023 г.
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Гиперболическая мозаика» . Математический мир .
- Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре» . Математический мир .
- Галерея гиперболических и сферических плиток
- KaleidoTile 3: образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик.
- Гиперболические плоские мозаики, Дон Хэтч



























































