Аксиомы Хузиты – Хатори

Аксиомы Хузиты-Джастина или аксиомы Хузиты-Хатори представляют собой набор правил, связанных с математическими принципами оригами , описывающих операции, которые можно выполнить при складывании листа бумаги. Аксиомы предполагают , что операции выполняются на плоскости (т. е. на идеальном листе бумаги) и что все складки линейны. Это не минимальный набор аксиом, а скорее полный набор возможных одиночных складок.

Первые семь аксиом были впервые обнаружены французским математиком Жаком Жюстеном в 1986 году. Аксиомы с 1 по 6 были заново открыты японско - итальянским математиком Хумиаки Хузитой и доложены на Первой международной конференции по оригами в образовании и терапии в 1991 году. Аксиомы с 1 по 5 были заново открыты Окли и Кливлендом в 1995 году. Аксиома 7 была заново открыта Косиро Хатори в 1995 году. 2001 г.; Роберт Дж. Лэнг также нашел аксиому 7.

Семь аксиом

Первые шесть аксиом известны как аксиомы Джастина или аксиомы Хузиты. Аксиома 7 была открыта Жаком Жюстином . Косиро Хатори и Роберт Дж. Лэнг также нашли аксиому 7. Аксиомы следующие:

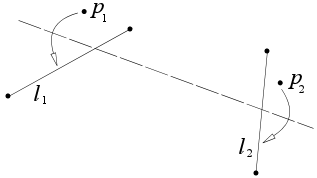
1. Учитывая две различные точки и _{существует единственная складка ,} p2 , _p1 проходящая через обе.
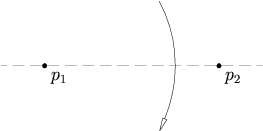
2. точки p1 _{которая} и p2 _, существует единственная складка, p1 _{помещает} на p2 _{Учитывая две различные} .
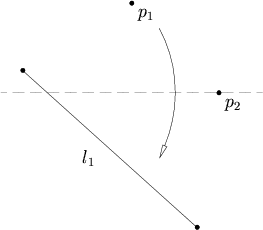
3. Даны две прямые l ₁ и l ₂ , существует складка, которая помещает l ₁ на l ₂ .
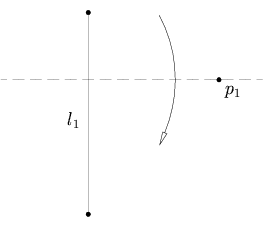
4. точки p1 _{Для данной} и прямой l1 _, существует единственная складка, перпендикулярная которая _{проходит} через точку p1 _l1 .
5. Учитывая две точки p1 _и и p2 _{которая} прямую l1 _p2 существует складка, p1 _{помещает} на l1 _, через и _{проходит} .
6. точки p1 _и две p2 _, прямые l1 _l1 и l2 _и существует складка p1 _{которая} на и _l2 . p2 _на две , _{помещает} Учитывая
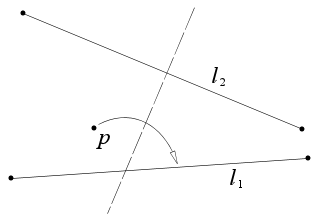
7. Учитывая одну точку p и две прямые l ₁ и l ₂ , существует складка, которая помещает точку p на l ₁ и перпендикулярна l ₂ .

Аксиома 5 может иметь 0, 1 или 2 решения, а аксиома 6 может иметь 0, 1, 2 или 3 решения. Таким образом, результирующая геометрия оригами сильнее, чем геометрия циркуля и линейки , где максимальное число решений аксиомы равно 2. Таким образом, геометрия циркуля и линейки решает уравнения второй степени, в то время как геометрия оригами, или оригами, может решать уравнения третьей степени и решать такие задачи, как трисекция угла и удвоение куба . Построение сгиба, гарантированное Аксиомой 6, требует «скольжения» бумаги, или neusis , что не допускается в классических конструкциях циркуля и линейки. Использование неусиса вместе с циркулем и линейкой позволяет выполнить трисекцию произвольного угла.

Подробности

Аксиома 1

Учитывая две точки p1 _{существует единственная складка ,} и p2 _, проходящая через обе.

В параметрической форме уравнение линии, проходящей через две точки, имеет вид:

$F(s)=p_{1}+s(p_{2}-p_{1}).$

Аксиома 2

две точки p1 _{которая} и p2 _p1 существует единственная складка, , _{помещает} на p2 _{Учитывая} .

Это эквивалентно нахождению серединного перпендикуляра отрезка p ₁ p ₂ . Это можно сделать в четыре шага:

• Используйте аксиому 1 чтобы найти линию, проходящую через и _, p2 , _p1 заданную формулой $P(s)=p_{1}+s(p_{2}-p_{1})$
• Найдите середину p ​ _{середине} в P ( s )
• Найдите вектор v ^{преступник} перпендикуляр к P ( s )
• Тогда параметрическое уравнение складки имеет вид:

$F(s)=p_{\mathrm {mid} }+s\cdot \mathbf {v} ^{\mathrm {perp} }.$

Аксиома 3

Даны две прямые l ₁ и l ₂ , существует складка, которая помещает l ₁ на l ₂ .

Это эквивалентно нахождению биссектрисы угла между l ₁ и l ₂ . Пусть p1 _q1 и p2 _— любые две точки на и _, пусть q2 _и — любые _две точки на l2 _l1 . Кроме того, пусть u и v будут единичными векторами направления l ₁ и l ₂ соответственно; то есть:

$\mathbf {u} =(p_{2}-p_{1})/\left|(p_{2}-p_{1})\right|$

$\mathbf {v} =(q_{2}-q_{1})/\left|(q_{2}-q_{1})\right|.$

Если две линии не параллельны, их точка пересечения:

$p_{\mathrm {int} }=p_{1}+s_{\mathrm {int} }\cdot \mathbf {u}$

где

$s_{int}=-{\frac {\mathbf {v} ^{\perp }\cdot (p_{1}-q_{1})}{\mathbf {v} ^{\perp }\cdot \mathbf {u} }}.$

Тогда направление одной из биссектрис будет:

$\mathbf {w} ={\frac {\left|\mathbf {u} \right|\mathbf {v} +\left|\mathbf {v} \right|\mathbf {u} }{\left|\mathbf {u} \right|+\left|\mathbf {v} \right|}}.$

И параметрическое уравнение складки:

$F(s)=p_{\mathrm {int} }+s\cdot \mathbf {w} .$

Также существует вторая биссектриса, перпендикулярная первой и проходящая через p _int . Складывание вдоль этой второй биссектрисы также позволит достичь желаемого результата — размещения l ₁ на l ₂ . В зависимости от расположения точки пересечения может оказаться невозможным выполнить ту или иную из этих сгибов.

Если две прямые параллельны, у них нет точки пересечения. Сгиб должен представлять собой линию посередине между l ₁ и l ₂ и параллельную им.

Аксиома 4

точки p1 _{Для данной} и прямой l1 _, существует единственная складка, перпендикулярная которая _{проходит} через точку p1 _l1 .

Это эквивалентно нахождению перпендикуляра к l ₁ , проходящего через p ₁ . Если мы найдем некоторый вектор v , перпендикулярный прямой l ₁ , то параметрическое уравнение складки будет иметь вид:

$F(s)=p_{1}+s\cdot \mathbf {v} .$

Аксиома 5

Учитывая две точки p1 _и и p2 _{которая} прямую l1 _p2 существует складка, p1 _{помещает} на l1 _, через и _{проходит} .

Эта аксиома эквивалентна поиску пересечения прямой с окружностью, поэтому она может иметь 0, 1 или 2 решения. Линия определяется l ₁ , а центр круга находится в точке p ₂ , а радиус равен расстоянию от p ₂ до p ₁ . Если прямая не пересекает окружность, решений нет. Если прямая касается окружности, существует одно решение, а если прямая пересекает окружность в двух местах, существует два решения.

Если мы знаем две точки на линии ( x ₁ , y ₁ ) и ( x ₂ , y ₂ ), то линию можно параметрически выразить как:

$x=x_{1}+s(x_{2}-x_{1})$

$y=y_{1}+s(y_{2}-y_{1}).$

Пусть окружность определяется ее центром в точке p ₂ =( x _c , y _c ) с радиусом $r=\left|p_{1}-p_{2}\right|$. Тогда круг можно выразить как:

$(x-x_{c})^{2}+(y-y_{c})^{2}=r^{2}.$

Чтобы определить точки пересечения прямой с окружностью, подставим компоненты x и y уравнений для прямой в уравнение для окружности, что дает:

$(x_{1}+s(x_{2}-x_{1})-x_{c})^{2}+(y_{1}+s(y_{2}-y_{1})-y_{c})^{2}=r^{2}.$

Или, упрощенно:

$as^{2}+bs+c=0$

где:

$a=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

$b=2(x_{2}-x_{1})(x_{1}-x_{c})+2(y_{2}-y_{1})(y_{1}-y_{c})$

$c=x_{c}^{2}+y_{c}^{2}+x_{1}^{2}+y_{1}^{2}-2(x_{c}x_{1}+y_{c}y_{1})-r^{2}.$

Дальше просто решаем квадратное уравнение:

${\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.$

Если дискриминант b ² − 4 ac < 0, решений нет. Круг не пересекает линию и не касается ее. Если дискриминант равен 0, то существует единственное решение, в котором прямая касается окружности. А если дискриминант больше 0, существует два решения, представляющие две точки пересечения. Назовем решения d ₁ и d ₂ , если они существуют. У нас есть 0, 1 или 2 отрезка:

$m_{1}={\overline {p_{1}d_{1}}}$

$m_{2}={\overline {p_{1}d_{2}}}.$

Сгиб F ₁ ( s ), перпендикулярный m ₁ через его середину, поместит p ₁ на линию в точке d ₁ . Аналогично, сгиб F ₂ ( s ), перпендикулярный m ₂ через его середину, поместит p ₁ на линию в точке d ₂ . Это легко достигается применением Аксиомы 2. Таким образом, параметрические уравнения складок таковы:

${\begin{aligned}F_{1}(s)&=p_{1}+{\frac {1}{2}}(d_{1}-p_{1})+s(d_{1}-p_{1})^{\perp }\\[8pt]F_{2}(s)&=p_{1}+{\frac {1}{2}}(d_{2}-p_{1})+s(d_{2}-p_{1})^{\perp }.\end{aligned}}$

Аксиома 6

точки p1 _и две p2 _, прямые l1 _l1 и l2 _и существует складка p1 _{которая} на и _l2 . p2 _на две , _{помещает} Учитывая

Эта аксиома эквивалентна нахождению прямой, одновременно касающейся двух парабол, и ее можно считать эквивалентной решению уравнения третьей степени, поскольку обычно существует три решения. Две параболы имеют фокусы в точках p ₁ и p ₂ соответственно, с директрисами, определяемыми l ₁ и l ₂ соответственно.

Эта складка называется складкой Белоха в честь Маргариты П. Белох , которая в 1936 году показала с ее помощью, что оригами можно использовать для решения общих кубических уравнений.

Аксиома 7

Учитывая одну точку p и две прямые l ₁ и l _2, которые не параллельны, существует сгиб, который помещает точку p на l ₁ и перпендикулярен l ₂ .

Эта аксиома была первоначально открыта Жаком Жюстином в 1989 году, но была упущена из виду и была заново открыта Косиро Хатори в 2002 году. Роберт Дж. Лэнг доказал, что этот список аксиом дополняет аксиомы оригами.

Конструктивность

Подмножества аксиом можно использовать для построения различных наборов чисел. Первые три можно использовать с тремя заданными точками, не лежащими на одной линии, для выполнения того, что Альперин называет талиевыми конструкциями.

Первые четыре аксиомы с двумя заданными точками определяют систему, более слабую, чем конструкции циркуля и линейки : каждую фигуру, которую можно сложить с помощью этих аксиом, можно построить с помощью циркуля и линейки, но некоторые вещи можно построить с помощью циркуля и линейки, которые нельзя сложить с помощью циркуля и линейки. эти аксиомы. Числа, которые можно построить, называются числами оригами или числами Пифагора. Если расстояние между двумя заданными точками равно 1, то все конструируемые точки имеют форму $(\alpha ,\beta )$ где $\alpha$ и $\beta$ являются числами Пифагора. Числа Пифагора задаются наименьшим полем, содержащим рациональные числа и ${\sqrt {1+\alpha ^{2}}}$ в любое время $\alpha$ это такое число.

Добавление пятой аксиомы дает евклидовы числа , то есть точки, которые можно построить с помощью циркуля и линейки .

Добавив аксиому neusis 6, можно построить все конструкции циркуля-линейки и многое другое. В частности, конструктивными правильными многоугольниками с этими аксиомами являются те, у которых $2^{a}3^{b}\rho \geq 3$ стороны, где $\rho$ является произведением различных простых чисел Пьерпона . Конструкции с циркулем и линейкой позволяют $2^{a}\phi \geq 3$ стороны, где $\phi$ является произведением различных простых чисел Ферма . (Простые числа Ферма являются подмножеством простых чисел Пьерпона.)

Седьмая аксиома не позволяет строить дальнейшие аксиомы. Семь аксиом дают все возможные одноразовые конструкции, а не являются минимальным набором аксиом.

Восьмая аксиома

В 2017 году Лусеро заявил о существовании восьмой аксиомы, которую можно сформулировать так: вдоль заданной линии l ₁ существует складка . Новая аксиома была найдена после перебора всех возможных вхождений между конструктивными точками и прямыми на плоскости. Хотя он и не создает новую линию, он, тем не менее, необходим при фактическом складывании бумаги, когда требуется сложить слой бумаги вдоль линии, отмеченной на слое непосредственно под ним.

Внешние ссылки

• Геометрические конструкции оригами Томаса Халла
• Математическая теория конструкций и чисел оригами Роджера К. Альперина