Строительство Нейсиса

В геометрии неусис , ( νεῦσις ; от древнегреческого νεύειν (neuein) «наклоняться к»; множественное число: νεύσεις , neuseis ) — геометрический метод построения который использовался в древности греческими математиками .

Геометрическая конструкция

Конструкция neusis состоит из размещения элемента заданной длины ( $a$ ) между двумя заданными линиями ( $l$ и $m$ ) таким образом, что линейный элемент или его продолжение проходит через заданную точку $P.$ линейного То есть один конец линейного элемента должен лежать на $l$ другой конец на $m$ , при этом линейный элемент «наклонен» в сторону $P.$ ,

Точка $Р$ называется полюсом невиса, линия $l$ — директрисой или направляющей линией, а линия $m$ — линией захвата. Длина $а$ называется диастемой ( греч . διάστημα , букв. «расстояние»).

Построение неусиса можно осуществить с помощью маркированной линейки, вращающейся вокруг точки $Р$ (это можно сделать, вставив булавку в точку $Р$ и затем прижав линейку к булавке). На рисунке один конец линейки отмечен желтым глазком с перекрестием: это начало деления шкалы на линейке. Вторая отметка на линейке (голубой глазок) указывает расстояние $a$ от начала координат. Желтый глаз перемещается по линии $l$ до тех пор, пока синий глаз не совпадет с линией $m$ . Положение найденного таким образом элемента линии показано на рисунке темно-синей полосой.

Трисекция угла

Трисекция Нейсиса угла $θ > 135°$ , чтобы найти $φ = θ /3$ , используя только длину линейки. Радиус дуги равен длине линейки. Для углов $θ < 135°$ применяется та же конструкция, но с $P,$ выходящим за пределы $AB$ .

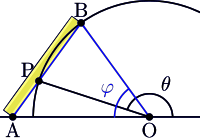
Нейзис можно использовать для разделения углов пополам следующими способами (см. изображение):

Для угла меньше 45° : отметьте на линейке радиус круга, затем переместите ее точку A по линии АО , удерживая B на ее краю, пока конец линейки не коснется круга — это будет точка «выше», чем B на круге (это будет похоже на изображение, за исключением того, что B и P перевернуты). Тогда угол POA будет равен 60° минус треть угла BOA . Например, если BOA = 27°, то POA будет равен 60° − (27 ÷ 3)° = 51°.
Для угла больше 45°, но меньше 90° : принцип тот же, за исключением того, что на этот раз A будет находиться на вертикальной линии, идущей вверх O. от
Для угла больше 90°, но меньше 135° : A все еще находится на вертикальной линии, идущей вверх O. от Однако пусть точка C где-нибудь на горизонтальной линии слева от O , а точка D — где-нибудь на горизонтальной линии справа от O. находится Угол POC теперь будет равен трети БПК .
Для угла больше 135° , но меньше 180° : на этот раз рисунок точно отображает ситуацию: точка D находится где-нибудь на горизонтальной линии справа от O , так что θ = ∠DOB. AB равно OP = OB .

Использование невиса

Neuseis были важны, потому что иногда они предоставляют средства для решения геометрических задач, которые невозможно решить только с помощью циркуля и линейки . Примерами являются трисечение любого угла на три равные части и удвоение куба . ^[1]^[2] Такие математики, как Архимед Сиракузский (287–212 до н. э.) и Папп Александрийский (290–350 н. э.), свободно использовали neuseis ; Сэр Исаак Ньютон (1642–1726) следовал их идеям и также использовал конструкции neusis. ^[3] Тем не менее постепенно техника вышла из употребления.

Правильные многоугольники

В 2002 году А. Барагар показал, что каждая точка, которую можно построить с помощью отмеченной линейки и циркуля, лежит в башне полей над $\mathbb {Q}$ , $\mathbb {Q} =K_{0}\subset K_{1}\subset \dots \subset K_{n}=K$ , такой, что степень расширения на каждом шаге не превышает 6. Из всех многоугольников простой степени ниже 128-угольника этого достаточно, чтобы показать, что правильные 23- , 29-, 43-, 47-, 49- угольник -, 53-, 59-, 67-, 71-, 79-, 83-, 89-, 103-, 107-, 113-, 121- и 127-угольники не могут быть построены с помощью невиса. (Если правильный p -угольник можно построить, то $\zeta _{p}=e^{\frac {2\pi i}{p}}$ является конструктивным, и в этих случаях p − 1 имеет простой делитель больше 5.) 3- , 4- , 5- , 6- , 8- , 10- , 12- , 15- , 16- , 17- , 20- , 24- , 30- , 32-, 34-, 40-, 48-, 51-, 60-, 64-, 68-, 80-, 85-, 96-, 102-, 120- и 128. -угольники можно построить только с помощью линейки и циркуля, а 7- , 9- , 13- , 14- , 18- , 19-, 21-, 26-, 27-, 28-, 35-, 36-, 37-, 38-, 39-, 42-, 52-, 54-, 56-, 57-, 63-, 65-, 70-, 72-, 73-, 74-, 76-, 78-, 81- , 84-, 91-, 95-, 97-, 104-, 105-, 108-, 109-, 111-, 112-, 114-, 117-, 119- и 126-угольники с трисекцией угла. Однако в целом неизвестно, имеют ли все квинтики (полиномы пятого порядка) конструируемые неусисом корни, что актуально для 11- , 25-, 31-, 41-, 61-, 101- и 125-угольников. . ^[4] Бенджамин и Снайдер показали в 2014 году, что правильный 11-угольник можно построить с помощью нейзиса; ^[1] 25-, 31-, 41-, 61-, 101- и 125-угольники остаются открытыми проблемами. В более общем смысле, возможность построения всех степеней 5, больших 5, с помощью помеченной линейки и циркуля является открытой проблемой, как и все простые числа больше 11, имеющие форму p = 2. ^р3 ^с5 ^т + 1, где t > 0 (все простые числа больше 11 и на единицу больше, чем обычное число , кратное 10). ^[4]

Убывающая популярность

Т. Л. Хит , историк математики, предположил, что греческий математик Энопид ( ок. 440 г. до н. э. ) был первым, кто поставил конструкции циркуля и линейки выше neuseis . Принцип по возможности избегать neuseis , возможно, был распространен Гиппократом Хиосским ( ок. 430 г. до н. э. ), который происходил с того же острова, что и Энопид, и который, насколько нам известно, был первым, кто написал систематически упорядоченный учебник геометрии. . Спустя сто лет после него Евклид тоже избегал neuseis в своем очень влиятельном учебнике «Элементы» .

Следующая атака на neusis произошла, когда начиная с четвертого века до нашей эры получил Платона идеализм распространение. Под его влиянием сложилась иерархия трех классов геометрических построений. Спускаясь от «абстрактного и благородного» к «механическому и земному», эти три класса были:

конструкции только с прямыми линиями и окружностями (циркуль и линейка);
конструкции, в которых помимо этого используются конические сечения ( эллипсы , параболы , гиперболы );
конструкции, требовавшие еще и других средств строительства, например neuseis .

В конце концов, использование неусиса было признано приемлемым только тогда, когда две другие, более высокие категории конструкций не предлагали решения. Нейсис стал своего рода последним средством, к которому прибегали только тогда, когда все другие, более респектабельные методы не дали результата. Использование неусиса там, где могли быть использованы другие методы построения, было заклеймено покойным греческим математиком Паппом Александрийским ( ок. 325 г. н.э. ) как «незначительная ошибка».

См. также

Ссылки

^ Jump up to: ^а ^б Бенджамин, Эллиот; Снайдер, К. (май 2014 г.). «О построении правильного семиугольника по размеченной линейке и циркулю» . Математические труды Кембриджского философского общества . 156 (3): 409–424. Бибкод : 2014MPCPS.156..409B . дои : 10.1017/S0305004113000753 . S2CID 129791392 . Архивировано (PDF) из оригинала 26 сентября 2020 г. Проверено 26 сентября 2020 г.
^ Вайсштейн, Эрик В. «Строительство Neusis». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/NeusisConstruction.html
^ Гвиччардини, Никколо (2009). Исаак Ньютон о математической достоверности и методе, выпуск 4 . МТИ Пресс . п. 68. ИСБН 9780262013178 .
^ Jump up to: ^а ^б Артур Барагар (2002) Конструкции с использованием циркуля и линейки с двумя надрезами, The American Mathematical Monthly, 109:2, 151-164, дои : 10.1080/00029890.2002.11919848

Р. Букер, «Нейсис», в: Настоящая энциклопедия классической древности Паули , Г. Виссова, ред. (1894–), Приложение 9 (1962) 415–461. – На немецком языке. Наиболее полное обследование; Однако у автора иногда возникают весьма любопытные мнения.
Т.Л. Хит , История греческой математики (2 тома; Оксфорд, 1921).
Х. Г. Цойтен , Теория конических сечений в древности (Копенгаген, 1886 г.; перепечатано в Хильдесхайме, 1966 г.).

Внешние ссылки

[ElliotConstruction-1] Jump up to: ^а ^б Бенджамин, Эллиот; Снайдер, К. (май 2014 г.). «О построении правильного семиугольника по размеченной линейке и циркулю» . Математические труды Кембриджского философского общества . 156 (3): 409–424. Бибкод : 2014MPCPS.156..409B . дои : 10.1017/S0305004113000753 . S2CID 129791392 . Архивировано (PDF) из оригинала 26 сентября 2020 г. Проверено 26 сентября 2020 г.

[2] Вайсштейн, Эрик В. «Строительство Neusis». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/NeusisConstruction.html

[3] Гвиччардини, Никколо (2009). Исаак Ньютон о математической достоверности и методе, выпуск 4 . МТИ Пресс . п. 68. ИСБН 9780262013178 .

[Baragar-4] Jump up to: ^а ^б Артур Барагар (2002) Конструкции с использованием циркуля и линейки с двумя надрезами, The American Mathematical Monthly, 109:2, 151-164, дои : 10.1080/00029890.2002.11919848

[1]

[2]

[3]

[4]