График Лавеса

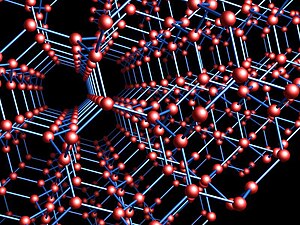
В геометрии и кристаллографии граф Лавеса — это бесконечная и высокосимметричная система точек и отрезков в трёхмерном евклидовом пространстве , образующая периодический граф . Три сегмента одинаковой длины встречаются под углом 120 ° в каждой точке, и во всех циклах используется десять или более сегментов. Это кратчайший возможный тройной периодический граф относительно объема его фундаментальной области . Один из вариантов графа Лавеса использует одну из каждых восьми точек целочисленной решетки в качестве своих точек и соединяет все пары этих точек, которые являются ближайшими соседями на расстоянии ${\sqrt {2}}$ . Его также можно определить, в отрыве от его геометрии, как абстрактный неориентированный граф , покрывающий полный граф на четырех вершинах.

HSM Coxeter ( 1955 ) назвал этот граф в честь Фрица Лавеса , который впервые написал о нем как о кристаллической структуре в 1932 году. ^[1]^[2] называют К4 _{кристаллом} . Его еще ^[3] (10,3)-сеть , ^[4] алмазный близнец , ^[5] третий мир , ^[6]^[7] и сеть SRS . ^[8] Области пространства, ближайшие к каждой вершине графа, представляют собой конгруэнтные 17-гранники, образующие плиточное пространство. Его ребра лежат на диагоналях правильного косого многогранника — поверхности с шестью квадратами, сходящимися в каждой целочисленной точке пространства.

Некоторые кристаллические химические вещества имеют известные или предсказанные структуры в форме графа Лавеса. Утолщение ребер графа Лавеса до цилиндров дает соответствующую минимальную поверхность , гироид , которая физически появляется в определенных структурах мыльной пленки и в крыльях бабочек.

Конструкции

Из целочисленной сетки

Правильный косой многогранник , в который можно вписать граф Лавеса. Ребра графа Лавеса являются диагоналями некоторых квадратов этой многогранной поверхности.

Как описывает Коксетер (1955) , вершины графа Лавеса могут быть определены путем выбора одной из каждых восьми точек в трехмерной целочисленной решетке и формирования графа их ближайших соседей . В частности, выбираются точки ${\begin{aligned}(0,0,0),\quad (1,2,3),\quad (2,3,1),\quad (3,1,2),\\(2,2,2),\quad (3,0,1),\quad (0,1,3),\quad (1,3,0),\\\end{aligned}}$ и все остальные точки, образованные добавлением к этим координатам числа, кратного четырем. Ребра графа Лавеса соединяют пары точек, евклидово расстояние которых друг от друга равно квадратному корню из двух , ${\sqrt {2}}$ , так как точки каждой пары различаются на одну единицу по двум координатам и совпадают по третьей координате. Края встречаются под углом 120° в каждой вершине в плоской плоскости. Все пары вершин, которые не являются соседними, находятся дальше друг от друга, на расстоянии не менее ${\sqrt {6}}$ друг от друга. Ребра полученного геометрического графа представляют собой диагонали подмножества граней правильного косого многогранника с шестью квадратными гранями на вершину, поэтому граф Лавеса вложен в этот косой многогранник. ^[1]

Можно выбрать больший набор из одной из каждых четырёх точек целочисленной решётки, так что график расстояний ${\sqrt {2}}$ пары этого большего набора образуют две зеркальные копии графа Лавеса, несвязанные друг с другом, причем все остальные пары точек находятся дальше, чем ${\sqrt {2}}$ отдельно. ^[9]

В качестве покрывающего графа

Как абстрактный граф, граф Лавеса может быть построен как максимальный абелев граф покрытия полного графа. $K_{4}$ . Будучи абелевым покрывающим графом $K_{4}$ означает, что вершины графа Лавеса могут быть четырехцветными, так что каждая вершина имеет соседей трех других цветов и что существуют сохраняющие цвет симметрии, переводящие любую вершину в любую другую вершину того же цвета. Для графа Лавеса в его геометрической форме с целочисленными координатами эти симметрии представляют собой сдвиги , которые добавляют четные числа к каждой координате (кроме того, смещения всех трех координат должны быть конгруэнтны по модулю четыре). При последовательном применении двух таких переводов итоговый перевод не зависит от их порядка: они коммутируют друг с другом, образуя абелеву группу . Векторы трансляции этой группы образуют трехмерную решетку . Наконец, то, что граф является максимальным абелевым накрывающим, означает, что не существует другого покрывающего графа для $K_{4}$ с участием решетки более высокой размерности. Эта конструкция оправдывает альтернативное название графа Лавеса — $K_{4}$ кристалл. ^[10]

Максимальный абелев граф покрытия можно построить из любого конечного графа $G$ ; применяется к $K_{4}$ , конструкция создает (абстрактный) граф Лавеса, но не дает ему той же геометрической структуры. Выберите связующее дерево из $G$ , позволять $d$ — количество ребер, которых нет в остовном дереве (в данном случае три ребра, не являющихся деревом), и выберите отдельный единичный вектор в $\mathbb {Z} ^{d}$ для каждого из этих недеревьевых ребер. Затем зафиксируем множество вершин покрывающего графа как упорядоченные пары $(v,w)$ где $v$ является вершиной $G$ и $w$ является вектором в $\mathbb {Z} ^{d}$ . Для каждой такой пары и каждого ребра $uv$ рядом с $v$ в $G$ , сделайте край из $(v,w)$ к $(u,w\pm \epsilon )$ где $\epsilon$ – нулевой вектор, если $uv$ принадлежит остовному дереву и в противном случае является базисным вектором, связанным с $uv$ , и где знак плюс или минус выбирается в зависимости от направления прохождения края. Полученный граф не зависит от выбранного остовного дерева, и ту же конструкцию можно интерпретировать более абстрактно, используя гомологии . ^[11]

Используя ту же конструкцию, гексагональная мозаика плоскости является максимальным абелевым графом покрытия трехреберного диполя , а алмазная кубика - максимальным абелевым графом покрытия четырехреберного диполя. $d$ -мерная целочисленная решетка (как граф с ребрами единичной длины) — это максимальный абелев накрывающий граф графа с одной вершиной и $d$ самопетли . ^[10]

В виде графика единичного расстояния

Граф единичных расстояний на трехмерной целочисленной решетке имеет вершину для каждой точки решетки; каждая вершина имеет ровно шесть соседей. Можно удалить часть точек из решетки так, чтобы у каждой оставшейся точки осталось ровно три соседа и чтобы в индуцированном подграфе этих точек не было циклов короче десяти ребер. Есть четыре способа сделать это, один из которых как абстрактный граф изоморфен графу Лавеса. Однако его вершины находятся в другом положении, чем у более симметричной традиционной геометрической конструкции. ^[12]

Другой подграф простой кубической сети, изоморфный графу Лавеса, получается удалением половины ребер определенным образом. Полученная структура, называемая полупростой кубической решеткой, также имеет более низкую симметрию, чем сам граф Лавеса. ^[13]

Характеристики

Граф Лавеса представляет собой кубический граф , что означает, что в каждой вершине имеется ровно три ребра. Любая пара вершины и смежного ребра может быть преобразована в любую другую такую пару благодаря симметрии графа, поэтому это симметричный граф . Более строго, для каждых двух вершин $u$ и $v$ , каждое взаимно однозначное соответствие между тремя ребрами, инцидентными $u$ и три ребра, инцидентные $v$ может быть реализовано посредством симметрии. Однако общая структура хиральна : никакая последовательность перемещений и вращений не может заставить ее совпасть со своим зеркальным отражением. ^[10] Группа симметрии графа Лавеса - это пространственная группа $I4_{1}32$ . ^[13]

Обхват этой структуры равен 10 — самые короткие циклы в графе имеют 10 вершин — и 15 из этих циклов проходят через каждую вершину. ^[10]^[1]^[9] Числа вершин на расстоянии 0, 1, 2, ... от любой вершины (образующие координационную последовательность графа Лавеса): ^[14]

1, 3, 6, 12, 24, 35, 48, 69, 86, 108, 138, 161, 192, 231, ... (последовательность A038620 в OEIS ).

Ячейки диаграммы Вороного графа Лавеса

Если окружающее пространство разбить на ближайшие к каждой вершине области — ячейки диаграммы Вороного этой структуры, — они образуют гептадекаэдры с 17 гранями в каждой. Это плезиоэдры , многогранники, которые замощают пространство изоэдрально . Экспериментируя со структурами, образованными этими многогранниками, физик Алан Шон открыл гироида минимальную поверхность . ^[15] что топологически эквивалентно поверхности, полученной утолщением ребер графа Лавеса до цилиндров и взятием границы их объединения. ^[16]

Граф Лавеса представляет собой единственную кратчайшую триждыпериодическую сеть в следующем смысле. Трижды периодическая означает бесконечное повторение во всех трех измерениях пространства, поэтому тройная периодическая сеть представляет собой связный геометрический граф с трехмерной решеткой трансляционных симметрий. — Фундаментальная область это любая форма, которая может замостить пространство своими транслированными копиями в соответствии с этими симметриями. Любая решетка имеет бесконечно много вариантов фундаментальной области различной формы, но все они имеют одинаковый объем. $V$ . Можно также измерить длину ребер сети в пределах одной копии фундаментальной области; позвони на этот номер $L$ . Аналогично $V$ , $L$ не зависит от выбора фундаментальной области, пока граница области пересекает только края, а не содержит части их длины. Граф Лавеса имеет четыре класса симметрии вершин ( орбит ), поскольку рассматриваемые здесь симметрии представляют собой всего лишь сдвиги, а не повороты, необходимые для отображения этих четырех классов друг в друга. Каждый класс симметрии имеет одну вершину в любой фундаментальной области, поэтому фундаментальная область содержит двенадцать полуребер общей длиной $6{\sqrt {2}}$ . Объем его фундаментальной области равен 32. Из этих двух чисел получается соотношение $L^{3}/V$ ( безразмерная величина ) поэтому $27/{\sqrt {2}}$ . Фактически это минимально возможное значение: все триждыпериодические сети имеют ${\frac {L^{3}}{V}}\geq {\frac {27}{\sqrt {2}}},$ с равенством только в случае графа Лавеса. ^[17]

Физические примеры

Искусство

Скульптура под названием Bamboozle работы Якобуса Верхуффа и его сына Тома Верхуффа представляет собой фрагмент графа Лавеса, вершины которого представлены разноцветными переплетающимися акриловыми треугольниками. Он был установлен в 2013 году в Технологическом университете Эйндховена . ^[18]

Молекулярные кристаллы

Граф Лавеса был предложен как аллотроп углерода , аналогичный более распространенной углеродной структуре графена и графита , которые также имеют три связи на атом под углами 120 °. ^[3]^[5] В графене соседние атомы имеют одинаковые плоскости связи, тогда как в структуре графа Лавеса плоскости связи соседних атомов закручены на угол примерно 70,5° вокруг линии связи. Однако этот гипотетический аллотроп углерода оказывается нестабильным. ^[19]

График Лавеса также может дать кристаллическую структуру бора , которая, как предсказывают вычисления, должна быть стабильной. ^[20] Другие химические вещества, которые могут образовывать эту структуру, включают SrSi ₂ (от которого происходит название «srs net»). ^[8] и элементарный азот , ^[9]^[20] а также некоторые металлоорганические каркасы ^[21] и циклические углеводороды . ^[22]

Была изучена электронная зонная структура для модели сильной связи графа Лавеса, показывающая существование точек Дирака и Вейля в этой структуре. ^[23]^[24]

Другой

Структура графа Лавеса и производных от него поверхностей гироида также наблюдалась экспериментально в системах мыльной воды и в хитиновых сетях чешуек крыльев бабочек . ^[9]

Ссылки

^ Перейти обратно: ^а ^б ^с Коксетер, HSM (1955), «О графике Лавеса обхвата десять», Canadian Journal of Mathematics , 7 : 18–23, doi : 10.4153/CJM-1955-003-7 , MR 0067508 , S2CID 124804911
^ Лавес, Ф. (1932), «К классификации силикатов. Геометрические исследования возможных кремний-кислородных соединений как возможности соединения правильных тетраэдров», Journal of Crystallography , 82 (1): 1–14, doi : 10.1524/zkri. 1932.82.1.1 , S2CID 101605313
^ Перейти обратно: ^а ^б Ито, Масахиро; Котани, Мотоко ; Наито, Хисаши; Сунада, Тошиказу ; Кавазоэ, Ёсиюки; Адшири, Тадафуми (2009), «Новый кристалл металлического углерода», Physical Review Letters , 102 (5): 055703, Bibcode : 2009PhRvL.102e5703I , doi : 10.1103/PhysRevLett.102.055703 , PMID 19257523
^ Уэллс, А. Ф. (1940), «X. Конечные комплексы в кристаллах: классификация и обзор», The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science , Series 7, 30 (199): 103–134, doi : 10.1080 /14786444008520702
^ Перейти обратно: ^а ^б Тагами, Макото; Лян, Юнье; Наито, Хисаши; Кавазоэ, Ёсиюки; Котани, Мотоко (2014), «Отрицательно изогнутые кубические кристаллы углерода с октаэдрической симметрией», Carbon , 76 : 266–274, doi : 10.1016/j.carbon.2014.04.077
^ Ланье, Джарон (2009), «От плоских структур к многогранникам» , American Scientist , 97:73 , doi : 10.1511/2009.76.73 .
^ Секен, Карло Х. (2008), «Сложные изоэдральные мозаики трехмерного евклидова пространства» , в Сарханги, Реза; Секин, Карло Х. (ред.), Бриджес Леуварден: математика, музыка, искусство, архитектура, культура , Лондон: Tarquin Publications, стр. 139–148, ISBN 9780966520194
^ Перейти обратно: ^а ^б Дельгадо Фридрихс, Олаф; О'Киф, Майкл; Яги, Омар М. (декабрь 2002 г.), «Трепериодические сети и мозаики: регулярные и квазирегулярные сети» (PDF) , Acta Crystallographica Раздел A: Основы кристаллографии , 59 (1): 22–27, doi : 10.1107/s0108767302018494 , hdl : 2027.42/115935 , PMID 12496458
^ Перейти обратно: ^а ^б ^с ^д Хайд, Стивен Т .; О'Киф, Майкл; Прозерпио, Давиде М. (2008), «Краткая история неуловимой, но повсеместно встречающейся структуры в химии, материалах и математике» (PDF) , Angewandte Chemie International Edition , 47 (42): 7996–8000, doi : 10.1002/anie .200801519 , PMID 18767088
^ Перейти обратно: ^а ^б ^с ^д Сунада, Тошиказу (2008), «Кристаллы, которые природа, возможно, не создала» (PDF) , Уведомления Американского математического общества , 55 (2): 208–215, MR 2375022 ; Сунада, Тошикадзу (2008), «Коррекция: кристаллы, которые природа могла упустить из виду» (PDF) , Уведомления Американского математического общества , 55 (3): 343
^ Биггс, Н.Л. (1984), «Гомологические покрытия графов», Журнал Лондонского математического общества , вторая серия, 30 (1): 1–14, doi : 10.1112/jlms/s2-30.1.1 , MR 0760867
^ Хаугланд, Ян Кристиан (2003), «Классификация некоторых подграфов трехмерной сетки», Journal of Graph Theory , 42 : 34–60, doi : 10.1002/jgt.10071 , MR 1943105 , S2CID 247671824
^ Перейти обратно: ^а ^б Кузьмин, доктор медицинских наук; Кузян, Р.О.; Рихтер, Дж. (2020), «Ферромагнетизм полупростой кубической решетки», The European Physical Journal Plus , 135 : 750, doi : 10.1140/epjp/s13360-020-00722-z .
^ Слоан, Нью-Джерси (редактор), «Последовательность A038620 (функция роста (или координационная последовательность) бесконечного кубического графа, соответствующего сети srs)» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS
^ Шон, Алан Х. (июнь – июль 2008 г.), «О графике (10,3)-a» (PDF) , Уведомления Американского математического общества , 55 (6): 663
^ Баэз, Джон (14 октября 2016 г.), «График Лавеса» , Visual Insight , Американское математическое общество
^ Алекс, Джером; Гроссе-Браукманн, Карстен (2017), Периодические сети Штейнера, минимизирующие длину , arXiv : 1705.02471 ; Алекс, Джером (2019), Периодическая задача Штейнера (докторская диссертация), Технический университет Дармштадта
^ Верховофф, Том; Верховев, Коос (2013), «Сложенные полоски ромбов и призыв к ${\sqrt {2}}:1$ ромб» , в Харте, Джордже У .; Сарханги, Реза (ред.), Proceedings of Bridges 2013: Mathematics, Music, Art, Architecture, Culture , Phoenix, Arizona: Tessellations Publishing, стр. 71–78, ISBN 978-1-938664-06-9 ; см. также Bamboozle: A Mathematical Artwork в MetaForum , Foundation MathArt Koos Verhoeff , получено 20 августа 2022 г.
^ Лян, Ю.; Чжан, В.; Чен, Л. (2009), «Фазовая стабильность и механические свойства двух новых кристаллов углерода», EPL , 87 (5): 56003, Bibcode : 2009EL.....8756003L , doi : 10.1209/0295-5075/87/ 56003 , S2CID 119424557
^ Перейти обратно: ^а ^б Дай, Джун; Ли, Чжэньюй; Ян, Цзиньлун (2010), «Кристалл бора K ₄ : стабильный хиральный трехмерный sp ² сеть», Physical Chemistry Chemical Physics , 12 (39): 12420–12422, Bibcode : 2010PCCP...1212420D , doi : 10.1039/C0CP00735H , PMID 20820588
^ Ян, Хуэй; Ли, Те-ху; Ван, Фэй; Чжан, Цзянь (февраль 2012 г.), «Необычные гетерометаллические строительные блоки ZnMg(COO) ₃ для построения гомохирального металлоорганического каркаса srs-типа», Inorganic Chemistry Communications , 16 : 86–88, doi : 10.1016/j.inoche .2011.11.039
^ Фукунага, Тошия М.; Като, Такахидэ; Икемото, Коки; Исобе, Хироюки (февраль 2022 г.), «Минимальная клетка алмазного двойника с хиральностью», Proceedings of the National Academy of Sciences , 119 (7), Bibcode : 2022PNAS..11920160F , doi : 10.1073/pnas.2120160119 , PMC 8851511 , PMID 35131931
^ Кауфманн, Ральф М.; Хлебников Сергей; Вефриц-Кауфманн, Биргит (2012), «Особенности, ласточкиные хвосты и точки Дирака: анализ семейств гамильтонианов и приложения к проводным сетям, особенно гироиду», Annals of Physics , 327 (11): 2865–2884, arXiv : 1208.3262 , Bibcode : 2012AnPhy.327.2865K , doi : 10.1016/j.aop.2012.08.001 , S2CID 14972547
^ Цучиидзу, Масахиса (2016), «Трехмерные дисперсии Дирака и Вейля с более высоким спином в сильно изотропном $кристалле K 4$ », Physical Review B , 94 (19): 195426, arXiv : 1609.09762 , Bibcode : 2016PhRvB..94s5426T , doi : 10.1103/PhysRevB.94.195426 , S2CID 119098343

Внешние ссылки

Харт, Джордж У. , (10, 3)-сеть .
Слоан, Нью-Джерси (редактор), «Последовательность A046944 (количество самоизбегающих блужданий длины n на графе Лавеса)» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS
Слоан, Нью-Джерси (редактор), «Последовательность A290705 (Тэта-серия трехугольника)» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS

[coxeter-1] Перейти обратно: ^а ^б ^с Коксетер, HSM (1955), «О графике Лавеса обхвата десять», Canadian Journal of Mathematics , 7 : 18–23, doi : 10.4153/CJM-1955-003-7 , MR 0067508 , S2CID 124804911

[laves-2] Лавес, Ф. (1932), «К классификации силикатов. Геометрические исследования возможных кремний-кислородных соединений как возможности соединения правильных тетраэдров», Journal of Crystallography , 82 (1): 1–14, doi : 10.1524/zkri. 1932.82.1.1 , S2CID 101605313

[prl09-3] Перейти обратно: ^а ^б Ито, Масахиро; Котани, Мотоко ; Наито, Хисаши; Сунада, Тошиказу ; Кавазоэ, Ёсиюки; Адшири, Тадафуми (2009), «Новый кристалл металлического углерода», Physical Review Letters , 102 (5): 055703, Bibcode : 2009PhRvL.102e5703I , doi : 10.1103/PhysRevLett.102.055703 , PMID 19257523

[wells-4] Уэллс, А. Ф. (1940), «X. Конечные комплексы в кристаллах: классификация и обзор», The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science , Series 7, 30 (199): 103–134, doi : 10.1080 /14786444008520702

[tlnkk-5] Перейти обратно: ^а ^б Тагами, Макото; Лян, Юнье; Наито, Хисаши; Кавазоэ, Ёсиюки; Котани, Мотоко (2014), «Отрицательно изогнутые кубические кристаллы углерода с октаэдрической симметрией», Carbon , 76 : 266–274, doi : 10.1016/j.carbon.2014.04.077

[lanier-6] Ланье, Джарон (2009), «От плоских структур к многогранникам» , American Scientist , 97:73 , doi : 10.1511/2009.76.73 .

[sequin-7] Секен, Карло Х. (2008), «Сложные изоэдральные мозаики трехмерного евклидова пространства» , в Сарханги, Реза; Секин, Карло Х. (ред.), Бриджес Леуварден: математика, музыка, искусство, архитектура, культура , Лондон: Tarquin Publications, стр. 139–148, ISBN 9780966520194

[doy-8] Перейти обратно: ^а ^б Дельгадо Фридрихс, Олаф; О'Киф, Майкл; Яги, Омар М. (декабрь 2002 г.), «Трепериодические сети и мозаики: регулярные и квазирегулярные сети» (PDF) , Acta Crystallographica Раздел A: Основы кристаллографии , 59 (1): 22–27, doi : 10.1107/s0108767302018494 , hdl : 2027.42/115935 , PMID 12496458

[elusive-9] Перейти обратно: ^а ^б ^с ^д Хайд, Стивен Т .; О'Киф, Майкл; Прозерпио, Давиде М. (2008), «Краткая история неуловимой, но повсеместно встречающейся структуры в химии, материалах и математике» (PDF) , Angewandte Chemie International Edition , 47 (42): 7996–8000, doi : 10.1002/anie .200801519 , PMID 18767088

[sunada-10] Перейти обратно: ^а ^б ^с ^д Сунада, Тошиказу (2008), «Кристаллы, которые природа, возможно, не создала» (PDF) , Уведомления Американского математического общества , 55 (2): 208–215, MR 2375022 ; Сунада, Тошикадзу (2008), «Коррекция: кристаллы, которые природа могла упустить из виду» (PDF) , Уведомления Американского математического общества , 55 (3): 343

[biggs-11] Биггс, Н.Л. (1984), «Гомологические покрытия графов», Журнал Лондонского математического общества , вторая серия, 30 (1): 1–14, doi : 10.1112/jlms/s2-30.1.1 , MR 0760867

[haugland-12] Хаугланд, Ян Кристиан (2003), «Классификация некоторых подграфов трехмерной сетки», Journal of Graph Theory , 42 : 34–60, doi : 10.1002/jgt.10071 , MR 1943105 , S2CID 247671824

[kuzmin-13] Перейти обратно: ^а ^б Кузьмин, доктор медицинских наук; Кузян, Р.О.; Рихтер, Дж. (2020), «Ферромагнетизм полупростой кубической решетки», The European Physical Journal Plus , 135 : 750, doi : 10.1140/epjp/s13360-020-00722-z .

[oeis-14] Слоан, Нью-Джерси (редактор), «Последовательность A038620 (функция роста (или координационная последовательность) бесконечного кубического графа, соответствующего сети srs)» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS

[schoen-15] Шон, Алан Х. (июнь – июль 2008 г.), «О графике (10,3)-a» (PDF) , Уведомления Американского математического общества , 55 (6): 663

[baez-16] Баэз, Джон (14 октября 2016 г.), «График Лавеса» , Visual Insight , Американское математическое общество

[shortest-17] Алекс, Джером; Гроссе-Браукманн, Карстен (2017), Периодические сети Штейнера, минимизирующие длину , arXiv : 1705.02471 ; Алекс, Джером (2019), Периодическая задача Штейнера (докторская диссертация), Технический университет Дармштадта

[bamboozle-18] Верховофф, Том; Верховев, Коос (2013), «Сложенные полоски ромбов и призыв к ${\sqrt {2}}:1$ ромб» , в Харте, Джордже У .; Сарханги, Реза (ред.), Proceedings of Bridges 2013: Mathematics, Music, Art, Architecture, Culture , Phoenix, Arizona: Tessellations Publishing, стр. 71–78, ISBN 978-1-938664-06-9 ; см. также Bamboozle: A Mathematical Artwork в MetaForum , Foundation MathArt Koos Verhoeff , получено 20 августа 2022 г.

[lzc-19] Лян, Ю.; Чжан, В.; Чен, Л. (2009), «Фазовая стабильность и механические свойства двух новых кристаллов углерода», EPL , 87 (5): 56003, Bibcode : 2009EL.....8756003L , doi : 10.1209/0295-5075/87/ 56003 , S2CID 119424557

[boron-20] Перейти обратно: ^а ^б Дай, Джун; Ли, Чжэньюй; Ян, Цзиньлун (2010), «Кристалл бора K ₄ : стабильный хиральный трехмерный sp ² сеть», Physical Chemistry Chemical Physics , 12 (39): 12420–12422, Bibcode : 2010PCCP...1212420D , doi : 10.1039/C0CP00735H , PMID 20820588

[metorg-21] Ян, Хуэй; Ли, Те-ху; Ван, Фэй; Чжан, Цзянь (февраль 2012 г.), «Необычные гетерометаллические строительные блоки ZnMg(COO) ₃ для построения гомохирального металлоорганического каркаса srs-типа», Inorganic Chemistry Communications , 16 : 86–88, doi : 10.1016/j.inoche .2011.11.039

[mincage-22] Фукунага, Тошия М.; Като, Такахидэ; Икемото, Коки; Исобе, Хироюки (февраль 2022 г.), «Минимальная клетка алмазного двойника с хиральностью», Proceedings of the National Academy of Sciences , 119 (7), Bibcode : 2022PNAS..11920160F , doi : 10.1073/pnas.2120160119 , PMC 8851511 , PMID 35131931

[kkwk-23] Кауфманн, Ральф М.; Хлебников Сергей; Вефриц-Кауфманн, Биргит (2012), «Особенности, ласточкиные хвосты и точки Дирака: анализ семейств гамильтонианов и приложения к проводным сетям, особенно гироиду», Annals of Physics , 327 (11): 2865–2884, arXiv : 1208.3262 , Bibcode : 2012AnPhy.327.2865K , doi : 10.1016/j.aop.2012.08.001 , S2CID 14972547

[tsuchiizu-24] Цучиидзу, Масахиса (2016), «Трехмерные дисперсии Дирака и Вейля с более высоким спином в сильно изотропном $кристалле K 4$ », Physical Review B , 94 (19): 195426, arXiv : 1609.09762 , Bibcode : 2016PhRvB..94s5426T , doi : 10.1103/PhysRevB.94.195426 , S2CID 119098343

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]