Количественная генетика

Количественная генетика -это изучение количественных признаков , которые являются фенотипами , которые непрерывно варьируются, например, высота или масса, в отличие от фенотипов и генов, которые являются дискретно идентифицируемыми , такими как оцветные глаза или присутствие определенного биохимического.

Обе эти ветви генетики используют частоты различных аллелей гена в популяциях размножения ( гамодом ) и объединяют их с концепциями от простого наследования Менделия для анализа схем наследования в разных поколениях и потомками. В то время как генетика популяции может сосредоточиться на конкретных генах и их последующих метаболических продуктах, количественная генетика больше фокусируется на внешних фенотипах и делает только резюме основной генетики.

Из -за непрерывного распределения фенотипических значений количественная генетика должна использовать многие другие статистические методы (такие как величина эффекта , среднее значение и дисперсию ), чтобы связать фенотипы (атрибуты) с генотипами. Некоторые фенотипы могут быть проанализированы либо как дискретные категории, либо как непрерывные фенотипы, в зависимости от определения точек отсечения или от метрики, используемой для их количественной оценки. ^{[ 1 ]}^: 27–69 Сам Мендель должен был обсудить этот вопрос в своей знаменитой газете, ^{[ 2 ]} Особенно в отношении его атрибута гороха высокого/карлика , который фактически был получен путем добавления точки отсечения к «длине стебля». ^{[ 3 ]}^{[ 4 ]} Анализ локусов количественных признаков , или QTLS, ^{[ 5 ]}^{[ 6 ]}^{[ 7 ]} является более недавним дополнением к количественной генетике, связывая ее более непосредственно с молекулярной генетикой .

Генные эффекты

В диплоидных организмах среднее генотипическое «значение» (значение локуса) может быть определена аллелем «эффектом» вместе с эффектом доминирования , а также с помощью того, как гены взаимодействуют с генами в других локусах ( эпистаз ). Основатель количественной генетики - сэр Рональд Фишер - во многом воспринял это, когда он предложил первую математику этой отрасли генетики. ^{[ 8 ]}

Будучи статистиком, он определил эффекты генов как отклонения от центрального значения - обеспечивая использование статистических концепций, таких как среднее значение и дисперсия, которые используют эту идею. ^{[ 9 ]} Центральным значением, которое он выбрал для гена, была средняя точка между двумя противоположными гомо -зиготами в одном локусе. Отклонение оттуда к «большему» гомозиготному генотипу может быть названо « +a »; и поэтому это « -а » от той же средней точки до «меньшего» гомозиготного генотипа. Это эффект «аллеля», упомянутый выше. Гетерозиготическое отклонение от одной и той же средней точки может быть названо « D », что является эффектом «доминирования», упомянутым выше. ^{[ 10 ]} Диаграмма изображает идею. Однако в действительности мы измеряем фенотипы, и на рисунке также показано, как наблюдаемые фенотипы связаны с эффектами генов. Формальные определения этих эффектов распознают этот фенотипический фокус. ^{[ 11 ]}^{[ 12 ]} Эпистаз обратился к статистически как к взаимодействию (т. Е. Несоответствия), ^{[ 13 ]} Но эпигенетика предполагает, что может потребоваться новый подход.

Если 0 < d < a , доминирование рассматривается как частичное или неполное - в то время как d = a указывает на полное или классическое доминирование. Ранее D > A был известен как «чрезмерная доминирование». ^{[ 14 ]}

Атрибут гороха Менделя «Длина стебля» дает нам хороший пример. ^{[ 3 ]} Мендель заявил, что высокие истинные родители варьировались от 6 до 7 футов по длине стебля (183-213 см), что дало медиану 198 см (= P1). Короткие родители варьировались от 0,75 до 1,25 фута длины стебля (23 - 46 см), с округлой медианой 34 см (= P2). Их гибрид варьировался от 6 до 7,5 футов в длину (183–229 см), со средней 206 см (= F1). Среднее значение P1 и P2 составляет 116 см, что является фенотипическим значением гомозигот средней точки (MP). Аллель аффект ( а ) равен [P1-MP] = 82 см =-[P2-MP]. Эффект доминирования ( D ) равен [F1-MP] = 90 см. ^{[ 15 ]} Этот исторический пример четко иллюстрирует, как связаны значения фенотипа и эффекты генов.

Аллель и частоты генотипа

Чтобы получить средства, отклонения и другие статистики, как количества , так и их происшествие требуются . Эффекты генов (выше) обеспечивают основу для количеств : и частоты контрастных аллелей в оплодотворяющих гамете-пуле предоставляют информацию о случаях .

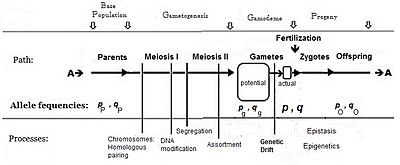
Обычно частота аллеля, вызывающего «больше» в фенотипе (включая доминирование), дается символ P , в то время как частота контрастного аллеля Q. составляет Первоначальным предположением, сделанным при установлении алгебры, было то, что родительская популяция была бесконечной и случайной спариванием, что было сделано просто для облегчения вывода. Последующая математическая разработка также подразумевает, что распределение частот в эффективном гамете было равномерным: не было локальных возмущений, где P и Q варьировались. Глядя на схематический анализ сексуального размножения, это то же самое, что заявление, что p _p = p _g = p ; аналогично Q. и ^{[ 14 ]} Эта система спаривания, зависящая от этих предположений, стала известна как «Панмиксия».

Панмиксия редко встречается в природе, ^{[ 16 ]}^{: 152–180}^{[ 17 ]} Поскольку распределение гамета может быть ограничено, например, ограничениями рассеивания или поведением или случайным отбором выборки (те локальные возмущения, упомянутые выше). Хорошо известно, что в природе существует огромная потери гаметов, поэтому на диаграмме изображена потенциальная гамета отдельно для фактического гаметового пула. Только последний устанавливает окончательные частоты для Zygotes: это истинная «Gamodeme» («Gamo» относится к гаметам, а «deme» происходит от греческого для «населения»). Но, согласно предположениям Фишера, Gamodeme может быть эффективно распространилась на потенциальную гамете-пилот и даже обратно к родительской базовой популяции («источник» население). Случайная выборка, возникающая, когда небольшие «фактические» гаметные пилоты отображаются из большого «потенциального» гамето-пула, известен как генетический дрейф и рассматривается впоследствии.

Хотя панмиксия может не быть широко распространенной, потенциал для нее возникает, хотя она может быть только эфемерной из -за этих местных возмущений. Например, было показано, что F2, полученный из случайного оплодотворения индивидуумов F1 ( аллогамный F2), после гибридизации, является происхождением новой потенциально панмиктической популяции. ^{[ 18 ]}^{[ 19 ]} Также было показано, что если панмиктическое случайное оплодотворение происходит постоянно, оно будет поддерживать одинаковые частоты аллеля и генотипа в каждом последовательном панмиктическом сексуальном поколении - это равновесие Харди Вайнберга . ^{[ 13 ]}^: 34–39^{[ 20 ]}^{[ 21 ]}^{[ 22 ]}^{[ 23 ]} Однако, как только генетический дрейф был инициирован локальной случайной выборкой гамет, равновесие прекратится.

Случайное оплодотворение

Обычно считается, что мужские и женские гаметы в реальном оплодотворяющем пуле имеют одинаковые частоты для соответствующих аллелей. (Исключения были рассмотрены.) Это означает, что, когда P -мужские гаметы, несущие аллель A , случайно оплодотворяют женские гаметы, несущие тот же аллель, полученная Zygote имеет генотип AA , и при случайном оплодотворе комбинация происходит с частотой P x p (= p ²) Точно так же Zygote AA происходит с частотой Q ²Полем Гетерозиготы ( AA ) могут возникнуть двумя способами: когда P Male ( аллель ) случайно оплодотворяет Q женских ( аллель ) гаметы, и наоборот . Полученная частота для гетерозиготных зигот, таким образом, 2pq . ^{[ 13 ]}^: 32 Обратите внимание, что такая популяция никогда не является более чем половиной гетерозиготной, это максимально происходит, когда P = Q = 0,5.

Таким образом, при случайном оплодотворении частоты Zygote (генотип) являются квадратичным расширением гаметических (аллельных) частот: ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ Полем («= 1» утверждает, что частоты находятся в форме фракции, а не в процентах; и что в предложенной структуре нет упущений.)

Обратите внимание, что «случайное оплодотворение» и «panmixia» не являются синонимами.

Исследовательский крест Менделя - контраст

Эксперименты по горохам Менделя были построены путем создания истинных родителей с «противоположными» фенотипами для каждого атрибута. ^{[ 3 ]} Это означало, что каждый противоположный родитель был гомозиготным только для соответствующего аллеля. В нашем примере «высокий против карлика» высоким родителем будет генотип TT с p = 1 (и Q = 0 ); в то время как карликовым родителем будет генотип TT с Q = 1 (и p = 0 ). После контролируемого пересечения их гибрид - TT , с p = Q = ⁠ 1/2 ⁠  . Однако частота этой гетерозиготы = 1 , потому что это F1 искусственного креста: она не возникла посредством случайного оплодотворения. ^{[ 24 ]} Генерация F2 была получена путем естественного самоопыления F1 (с мониторингом против загрязнения насекомых), что привело к P = Q = ⁠ 1/2 поддерживается ⁠ . Такой F2, как говорят, «аутогамный». Однако частоты генотипа (0,25 тт , 0,5 тт , 0,25 тт ) возникли через систему спаривания, сильно отличающиеся от случайного оплодотворения, и, следовательно, было избегано использования квадратичного расширения. Полученные численные значения были такими же, как и для случайного оплодотворения только потому, что это особый случай, как первоначально скрещенные гомозиготные противоположные родители. ^{[ 25 ]} Мы можем заметить, что из-за доминирования T- [частоты (0,25 + 0,5)] более TT [частота 0,25] соотношение 3: 1 все еще получается.

Крест, такой как «Мендель», где истинное размножение (в основном гомозиготные) противоположные родители пересекаются контролируемым способом для производства F1, является особым случаем гибридной структуры. F1 часто считается «совершенно гетерозиготным» для рассматриваемого гена. Тем не менее, это чрезмерное упрощение и не применяется в целом, например, когда отдельные родители не гомозиготны или когда популяции мешают гибридам с образованием гибридных роев . ^{[ 24 ]} Общие свойства внутривидовых гибридов (F1) и F2 (как «аутогамные», так и «аллогамные») рассматриваются в более позднем разделе.

Самочувствие - альтернатива

Заметив, что горох естественным образом самоопыляется, мы не можем продолжать использовать его в качестве примера для иллюстрации случайных свойств оплодотворения. Самопроблема («самоопыление») является основной альтернативой случайным оплодотворениям, особенно в растениях. Большинство злаков Земли естественным образом самоопыляются (например, рис, пшеница, ячмень), а также импульсы. Учитывая миллионы людей каждого из них на Земле в любое время, очевидно, что самоопределение, по крайней мере, столь же значимо, как и случайное оплодотворение. Самопроблема является наиболее интенсивной формой инбридинга , которая возникает всякий раз, когда существует ограниченная независимость в генетическом происхождении гаметов. Такое снижение независимости возникает, если родители уже связаны, и/или от генетического дрейфа или других пространственных ограничений на рассеивание гамета. Анализ пути демонстрирует, что они равносильны тому же. ^{[ 26 ]}^{[ 27 ]} Вытекающий из этого фона, коэффициент инбридинга (часто символизируется как f или f ) определяет влияние инбридинга по любой причине. Есть несколько формальных определений F , и некоторые из них рассматриваются в последующих разделах. Для настоящего обратите внимание, что для долгосрочных самоопределенных видов F = 1 . Однако естественные самоопределенные популяции-это не « чистые линии », а смеси таких линий. Это становится особенно очевидным при рассмотрении более одного гена за раз. Следовательно, частоты аллелей ( P и Q ), кроме 1 или 0, все еще актуальны в этих случаях (обратно в поперечное сечение Менделя). Однако частоты генотипа принимают другую форму.

В целом, частоты генотипа становятся ${\textstyle [p^{2}(1-f)+pf]}$ для AA и ${\textstyle 2pq(1-f)}$ для AA и ${\textstyle [q^{2}(1-f)+qf]}$ для аа . ^{[ 13 ]}^: 65

Обратите внимание, что частота гетерозиготы снижается пропорционально f . Когда F = 1 , эти три частоты становятся соответственно P , 0 и Q, наоборот, когда F = 0 , они сводятся к квадратичному расширению случайного оплодотворения, показанного ранее.

Население означает

Среднее число населения переводит центральную точку отсчета от гомозиготной средней точки ( MP ) в среднее значение сексуально воспроизводимого населения. Это важно не только для того, чтобы переместить фокус в мир природы, но и использовать меру центральной тенденции, используемой статистикой/биометрией. В частности, квадрат этого среднего является коррекционным фактором, который используется для получения генотипических дисперсий позже. ^{[ 9 ]}

Для каждого генотипа, в свою очередь, его эффект аллеля умножается на частоту генотипа; и продукты накапливаются по всем генотипам в модели. Некоторое алгебраическое упрощение обычно следует, чтобы достичь краткого результата.

Среднее среднее после случайного оплодотворения

Вклад АА ${\textstyle p^{2}(+)a}$ это АА , ${\textstyle 2pqd}$ и АА , ${\textstyle q^{2}(-)a}$ Полем Собравшись вместе с двумя терминами и накапливаясь над всеми, результат: ${\textstyle a(p^{2}-q^{2})+2pqd}$ Полем Упрощение достигается, отметив, что ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ и, вспомнив, что ${\textstyle (p+q)=1}$ , тем самым уменьшая правый термин ${\textstyle (p-q)}$ .

Следовательно, результат ${\textstyle G=a(p-q)+2pqd}$ . ^{[ 14 ]} ^: 110

Это определяет среднее население как «смещение» из гомозиготной средней точки (отзыв A и D определяются как отклонения от этой средней точки). На рисунке изображен G по всем значениям P для нескольких значений D , включая один случай небольшой чрезмерной доминирования. Обратите внимание, что G часто является отрицательным, тем самым подчеркивая, что это самооклонение ( от MP ).

Наконец, для получения фактического среднего значения популяции в «фенотипическом пространстве» значение средней точки добавляется к этому смещению: ${\textstyle P=G+mp}$ .

Пример возникает из данных о длине уха в кукурузе. ^{[ 28 ]}^: 103 Предполагая, что на данный момент представлен только один ген, A = 5,45 см, D = 0,12 см [практически «0», действительно], MP = 12,05 см. Кроме того, предполагая, что p = 0,6 и q = 0,4 в этом примере популяции, тогда:

G = 5,45 (0,6 - 0,4) + (0,48) 0,12 = 1,15 см (округлый); и

P = 1,15 + 12,05 = 13,20 см (округлый).

Среднее среднее после долгосрочной самоотверженности

Вклад АА ${\textstyle p(+a)}$ , в то время АА как ${\textstyle q(-a)}$ Полем [См. Выше для частот.] Сбор этих двух терминов вместе приводит к немедленно очень простому конечному результату:

${\textstyle G_{(f=1)}=a(p-q)}$ Полем Как и прежде, ${\textstyle P=G+mp}$ .

Часто «g _{(f = 1)} » сокращается до «G ₁ ».

Город Менделя может предоставить нам эффекты аллеля и среднюю точку (см. Ранее); и смешанная самоопыляемая популяция с p = 0,6 и Q = 0,4 дает примеры частоты. Таким образом:

G _{(F = 1)} = 82 (0,6 - .04) = 59,6 см (округлый); и

P _{(F = 1)} = 59,6 + 116 = 175,6 см (округлый).

Среднее - обобщенное оплодотворение

Общая формула включает в себя коэффициент инбридинга F , а затем может приспособиться к любой ситуации. Процедура точно такая же, как и раньше, используя взвешенные частоты генотипа, приведенные ранее. После перевода в наши символы и дальнейшая перестройка: ^{[ 13 ]} ^: 77–78

${\begin{aligned}G_{f}&=a(q-p)+[2pqd-f(2pqd)]\\&=a(p-q)+(1-f)2pqd\\&=G_{0}-f\ 2pqd\end{aligned}}$ Здесь G ₀ - G , который был дан ранее. (Часто, когда имея дело с инбридингом, «G ₀ » предпочитает «G».)

Предположим, что пример кукурузы [приведенный ранее] был ограничен на холме (узкий прибрежный луг), и имел частичное инбридинги в той мере, что и F = 0,25 , тогда используя третью версию (выше) G _F :

G _0,25 = 1,15 - 0,25 (0,48) 0,12 = 1,136 см (округлый), с р _0,25 = 13,194 см (округлый).

В этом примере почти не существует эффекта от инбридинга, который возникает из -за того, что в этом атрибуте практически не было доминирования ( D → 0). Исследование всех трех версий G _F показывает, что это приведет к тривиальным изменениям в среднем населении. Там, где господство было примечательно, однако, произошли бы значительные изменения.

Генетический дрейф

Генетический дрейф был введен при обсуждении вероятности того, что панмиксия широко существует как естественная картина оплодотворения. [См. Раздел о частотах аллеля и генотипа.] Здесь дискретизация гаметов из потенциальной Gamodeme обсуждается более подробно. Отбор выборки включает в себя случайное оплодотворение между парами случайных гамет, каждая из которых может содержать либо A , либо A A A Allele. Таким образом, выборка является биномиальной выборкой. ^{[ 13 ]}^{: 382–395}^{[ 14 ]}^: 49–63^{[ 29 ]}^: 35^{[ 30 ]}^: 55 Каждый выборка «пакета» включает 2N -аллели и производит N в результате Zygotes («потомство» или «линия»). В течение репродуктивного периода этот выборка повторяется снова и снова, так что конечным результатом является смесь потомков образца. Результатом является рассеянное случайное оплодотворение $\left(\bigodot \right)$ Эти события и общий конечный результат изучаются здесь с иллюстративным примером.

Частоты аллелей «базовых» примеров - это частота потенциальной Gamodeme : частота A равен P _g = 0,75 , в то время как частота a равна q _g = 0,25 . [ Белая метка « 1 » на диаграмме.] Пять примеров Фактических агодеми биномиально отображаются из этой основы ( s = количество образцов = 5), и каждый образец обозначен с «индексом» k : с k = 1. ... S последовательно. (Это выборка «пакеты», упомянутые в предыдущем абзаце.) Количество гаметов, участвующих в оплодотворенности, варьируется от образца к образцу и дается как 2n _K [на белой метке « 2 » на диаграмме]. Общее (σ) количество гамет, отобранных в целом, составляет 52 [ белая метка " 3 " на диаграмме]. Поскольку каждый образец имеет свой собственный размер, веса необходимы для получения средних значений (и других статистических данных) при получении общих результатов. Это ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ , и даны на белой ярлыке « 4 » на диаграмме.

Образец Gamodemes - генетический дрейф

После завершения этих пяти событий биномиальной выборки, результирующие фактические агодеми содержали разные частоты аллелей - ( P _K и Q _K ). [Они приведены на белой метке « 5 » на диаграмме.] Этот результат на самом деле является самого генетического дрейфа. Обратите внимание, что два образца (k = 1 и 5) имеют одинаковые частоты, что и базовая ( потенциальная ) Гамадема. У другого (k = 3) есть p и q ". Образец (k = 2) является «экстремальным» случаем, с p _k = 0,9 и q _k = 0,1 ; в то время как оставшаяся выборка (k = 4) является «средней диапазоном» на частотах его аллелей. Все эти результаты возникли только по «случайности» посредством биномиальной выборки. Однако, произошедшие, они установили все нисходящие свойства потомков.

Поскольку выборка включает в себя случайность, вероятности ( $\int$ _k ) получения каждого из этих образцов представляют интерес. Эти биномиальные вероятности зависят от начальных частот ( P _G и Q _G ) и размера выборки ( 2n _K ). Они утомительны, чтобы получить, ^{[ 13 ]}^{: 382–395}^{[ 30 ]}^: 55 но представляют значительный интерес. [См. Белую метку « 6 » на диаграмме.] Два образца (k = 1, 5), с частотами аллелей, так же, как в потенциальной гамадеме , имели более высокие «шансы», чем другие образцы. Однако их биномиальные вероятности отличались из -за их различных размеров выборки (2n _k ). Выборка «разворота» (k = 3) имела очень низкую вероятность возникновения, подтверждая, возможно, то, что можно ожидать. Однако «экстремальная» частота аллеля (k = 2) не была «редкой»; и выборка «середина диапазона» (k = 4) была редкой. Эти же вероятности применяются также к потомству этих удобрений.

Здесь некоторые суммирование может начаться. Общие частоты аллелей в объеме потомков поставляются по взвешенным средним значениям соответствующих частот отдельных образцов. То есть: ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ и ${\textstyle q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ q_{k}}$ Полем (Обратите внимание, что K заменяется на • Для общего результата - обычной практики.) ^{[ 9 ]} Результаты для примера являются p _• = 0,631 и Q _• = 0,369 [ черная метка " 5 " на диаграмме]. Эти значения весьма отличаются от начальных ( P _G и Q _G ) [ белая метка " 1 "]. Частоты аллелей выборки также имеют дисперсию, а также в среднем. Это было получено с использованием суммы квадратов (SS) метода ^{[ 31 ]} [Смотрите справа от черной метки « 5 » на диаграмме]. [Дальнейшее обсуждение этой дисперсии происходит в разделе ниже об обширном генетическом дрейфе.]

Линии потомства - дисперсия

Частоты генотипа пяти потомков образца получены из обычного квадратичного расширения их соответствующих частот аллелей ( случайное оплодотворение ). диаграммы Результаты даются на белой этикетке « 7 » для гомозигот, а на белой ярлыке « 8 » для гетерозигот. Повторное устройство таким образом подготавливает путь для мониторинга уровней инбридинга. Это можно сделать либо путем изучения уровня общего гомозигоза [( P ²_K + Q. ²_k ) = ( 1 - 2p _k q _{k k} )], или путем изучения уровня гетерозигоза ( 2p _k q _k ), так как они дополняют. ^{[ 32 ]} Обратите внимание, что образцы k = 1, 3, 5 имели одинаковый уровень гетерозигоза, несмотря на то, что одним из них является «зеркальное изображение» других в отношении частот аллелей. У «экстремального» аллель -частотного случая (k = 2 ) был самый гомозигоз (наименьший гетерозигоз) любого образца. В случае «середины диапазона» (k = 4 ) была наименьшая гомозиготность (большая часть гетерозиготности): каждый из них был равен в 0,50, на самом деле.

Общее резюме может продолжаться путем получения среднего значения соответствующих частот генотипа для потомства. Таким образом, для АА это ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$ , для AA , это ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ И для АА это ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$ Полем Результаты примера приведены на черной ярлыке « 7 » для гомозигот, а на черной метке « 8 » для гетерозиготы. Обратите внимание, что среднее значение гетерозиготности составляет 0,3588 , которое используется в следующем разделе для изучения инбридинга в результате этого генетического дрейфа.

Следующим центром интереса является сама дисперсия, которая относится к «распространению» населения потомков . Они получены как ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ [См. Раздел о среднем популяции], для каждого образца потомства, в свою очередь, используя пример эффектов генов, приведенных на белой метке « 9 » на диаграмме. Тогда каждый ${\textstyle P_{k}=G_{k}+mp}$ получается также [на белой метке " 10 " на диаграмме]. Обратите внимание, что «лучшая» линия (k = 2) имела самую высокую частоту аллеля для аллеля «больше» ( а ) (у нее также был самый высокий уровень гомозиготности). Худшее потомство (k = 3) имело самую высокую частоту для аллеля «меньше» ( а ), который учитывал его плохую работу. Эта «плохая» линия была менее гомозиготной, чем «лучшая» линия; и на самом деле он разделял тот же уровень гомозиготности, что и две вторые лучшие линии (k = 1, 5). Линия потомства как с «большим», так и с аллелями «меньше», присутствующих на одинаковой частоте (k = 4), имела среднее значение ниже общего среднего (см. Следующий параграф) и имела самый низкий уровень гомозиготности. Эти результаты показывают тот факт, что аллели, наиболее распространенные в «ген-пуле» (также называемой «зародышевой плазмы»), определяют производительность, а не уровень гомозиготности как таковой. Единственная биномиальная выборка влияет на эту дисперсию.

Общее резюме теперь можно завершить путем получения ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ и ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$ Полем Пример результата для P _• 36,94 ( черная метка « 10 » на диаграмме). Это позже используется для количественной оценки депрессии инбридинга в целом, от выборки гамета. [См. Следующий раздел.] Однако напомним, что некоторые «не депрессированные» средства потомства уже были идентифицированы (K = 1, 2, 5). Это загадка инбридинга - в то время как в целом может быть «депрессия», среди выборов Gamodeme обычно есть превосходные линии.

Эквивалентная постдисперсия панмикта-инбридинга

В общее резюме были включены средние частоты аллелей в смеси линий потомства ( P _• и Q _• ). Теперь они могут быть использованы для построения гипотетического панмиктического эквивалента. ^{[ 13 ]}^{: 382–395}^{[ 14 ]}^: 49–63^{[ 29 ]}^: 35 Это можно рассматривать как «ссылку» для оценки изменений, внесенных выборкой гамета. Пример добавляет такую панмикцию справа от диаграммы. частота АА Поэтому (P _• ) ² = 0,3979. Это меньше, чем то, что можно найти в рассеиваемой объеме (0,4513 на черной метке " 7 "). Точно так же для AA , (Q _• ) ² = 0,1303 - опять же меньше, чем эквивалент в объеме потомков (0,1898). Очевидно, что генетический дрейф увеличил общий уровень гомозигоза на количество (0,6411 - 0,5342) = 0,1069. В дополнительном подходе вместо этого можно использовать гетерозиготность. Панмиктный эквивалент для AA составляет 2 P _• Q _• = 0,4658, что выше , чем в выбранной объеме (0,3588) [ черная метка " 8 "]. Отбор проб приводил к снижению гетерозиготности на 0,1070, что тривиально отличается от более ранней оценки из -за ошибок округления.

Коэффициент инбридинга ( F ) был введен в раннем разделе о самочувствии. Здесь рассматривается формальное определение этого: f - это вероятность того, что два «одних» аллелях (то есть или , и a a и a ) , которые оплодотворяют вместе общее происхождение - или (более формально) f - это вероятность того, что два гомологичных аллеля являются аутозиготными. ^{[ 14 ]}^{[ 27 ]} Рассмотрим любую случайную гамету в потенциальной Gamodeme, которая ограничивает его сингамию партнера, ограниченного биномиальной выборкой. Вероятность того, что этот второй гамет является гомологичной аутозиготной до первого, составляет 1/(2n) , что является взаимным размером гамдеми. Для пяти примеров потомков эти величины составляют 0,1, 0,0833, 0,1, 0,0833 и 0,125 соответственно, а их средневзрсия составляет 0,0961 . Это коэффициент инбридинга примеров примера потомков, при условии, что он непредвзят в отношении полного биномиального распределения. Однако пример, основанный на S = 5, может быть смещен, однако, по сравнению с соответствующим целым биномиальным распределением на основе числа выборки ( ы ), приближающихся к бесконечности ( S → ∞ ). Другое полученное определение F для полного распределения заключается в том, что F также равняется росту гомозиготности, что равняется падению гетерозиготности. ^{[ 33 ]} Для примера эти изменения частоты составляют 0,1069 и 0,1070 соответственно. Этот результат отличается от вышеперечисленного, указывая на то, что в примере присутствует смещение по отношению к полному базовому распределению. примера Для самого эти последние значения являются лучшими для использования, а именно F _• = 0,10695 .

Среднее значение популяции эквивалентной панмикции обнаруживается как [a (p _• -q _• ) + 2 p _• q _• d] + mp . Используя пример эффектов гена ( белая метка « 9 » на диаграмме), это означает ${\textstyle P_{\centerdot }=}$ 37.87. Эквивалентное среднее значение в дисперсированной объеме составляет 36,94 ( черная метка " 10 "), что подавлено суммой 0,93 . Это депрессия инбридинга от этого генетического дрейфа. Однако, как отмечалось ранее, три потомства не были подавлены (K = 1, 2, 5) и имели средства, даже больше, чем у панмиктического эквивалента. Это линии, которые заводчик растений ищет в программе выбора линии. ^{[ 34 ]}

Обширная биномиальная выборка - восстановлена ли панмиксия?

Если количество биномиальных образцов большое ( → ∞ ), то P _• → P _G и Q _• → Q _G. S Можно запрашивать, будет ли Панмиксия эффективно вновь появляться в этих обстоятельствах. Тем не менее, выборка частот аллелей , по -прежнему произошла в результате чего σ ²_{P, Q} ♠ 0 . ^{[ 35 ]} На самом деле, как s → ∞ , ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ , который является дисперсией всего биномиального распределения . ^{[ 13 ]}^{: 382–395}^{[ 14 ]}^: 49–63 частоты потомков Кроме того, «уравнения Wahlund» показывают, что гомозиготные можно получить в качестве сумм их соответствующих средних значений ( P ²_• или Q. ²_• ) плюс σ ²_P, Q. ^{[ 13 ]}^{: 382–395} Аналогично, объемная гетерозиготная частота составляет p _• q _• ) минус дважды σ ( 2 ²_P, Q. Разница, возникающая в результате биномиальной выборки, явно присутствует. Таким образом, даже при S → ∞ Bulk Bulk частоты генотипа по-прежнему выявляют повышенный гомозигоз и снижение гетерозигоза , все еще существует дисперсия средств потомства и все еще инбридинга и инбридинга . То есть панмиксия не переосмыслена, когда-то потерялась из-за генетического дрейфа (биномиальная выборка). Тем не менее, новая потенциальная панмиксия может быть инициирована с помощью аллогамного F2 после гибридизации. ^{[ 36 ]}

Продолжение генетического дрейфа - повышение дисперсии и инбридинга

Предыдущее обсуждение генетического дрейфа изучало только один цикл (поколение) процесса. Когда выборка продолжается в последовательных поколениях, в σ происходят заметные изменения в σ ²_{P , Q} и F. Кроме того, необходим еще один «индекс», чтобы отслеживать «время»: t = 1 .... y , где y = количество «лет» (поколения). Методология часто заключается в том, чтобы добавить текущий биномиальный приращение ( Δ = " de novo ") к тому, что произошло ранее. ^{[ 13 ]} Все биномиальное распределение рассматривается здесь. [Не существует дополнительной выгоды от сокращенного примера.]

Дисперсия через σ ²_{P, Q.}

Ранее эта дисперсия (σ ²_{P, Q.}^{[ 35 ]}) считалось:- ${\begin{aligned}\sigma _{p,q}^{2}&=p_{g}q_{g}\ /\ 2N\\&=p_{g}q_{g}\left({\frac {1}{2N}}\right)\\&=p_{g}q_{g}\ f\\&=p_{g}q_{g}\ \Delta f\ \scriptstyle {\text{when used in recursive equations}}\end{aligned}}$

С расширением с течением времени это также является результатом первого цикла, как и ${\textstyle \sigma _{1}^{2}}$ (для краткости). В цикле 2 эта дисперсия снова генерируется - это время становится дисперсией de novo ( ${\textstyle \Delta \sigma ^{2}}$ )-и накапливается до того, что уже присутствовало-дисперсию «переноса». Вторая дисперсия цикла ( ${\textstyle \sigma _{2}^{2}}$ ) - взвешенная сумма этих двух компонентов, веса ${\textstyle 1}$ для снова и ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ = ${\textstyle \left(1-\Delta f\right)}$ для «переноски».

Таким образом,

\sigma _{2}^{2}=\left(1\right)\ \Delta \sigma ^{2}+\left(1-\Delta f\right)\sigma _{1}^{2}

( 1 )

Расширение на обобщение на любое время t после значительного упрощения становится: ^{[ 13 ]}^: 328-

\sigma _{t}^{2}=p_{g}q_{g}\left[1-\left(1-\Delta f\right)^{t}\right]

( 2 )

Поскольку именно это изменение в частотах аллелей вызвало «распространение» средств потомков ( дисперсия ), изменение σ ²_T в течение поколений указывают изменение уровня дисперсии .

Дисперсия через f

Метод изучения коэффициента инбридинга аналогичен тем, который используется для σ ²_P, Q. Те же веса, что и раньше, используются соответственно для de novo f ( Δ f ) [Напомним, что это 1/(2n) ] и перенос f . Поэтому, ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ , что похоже на уравнение (1) в предыдущем подразделе.

В общем, после перестройки, ^{[ 13 ]} ${\begin{aligned}f_{t}&=\Delta f+\left(1-\Delta f\right)f_{t-1}\\&=\Delta f\left(1-f_{t-1}\right)+f_{t-1}\end{aligned}}$ Графики слева показывают уровни инбридинга более двадцати поколений, возникающих в результате генетического дрейфа для различных фактических размеров Gamodeme (2n).

Еще дальнейшие перестройки этого общего уравнения показывают некоторые интересные отношения.

(А) После некоторого упрощения, ^{[ 13 ]} ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ Полем Левая сторона-это разница между текущими и предыдущими уровнями инбридинга: изменение инбридинга ( ΔF _T ). Обратите внимание, что это изменение инбридинга ( ΔF _T ) равно инбридингу De novo ( ΔF ) только для первого цикла-когда F _T-1 равен нулю .

(B) Примечание-это (1-F _T-1 ) , который является «индексом неинбридинга ». Он известен как панмиктический индекс . ^{[ 13 ]}^{[ 14 ]} ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ .

(C) Появляются дальнейшие полезные отношения с участием панмиктического индекса . ^{[ 13 ]}^{[ 14 ]} ${\begin{aligned}\Delta f&={\frac {\delta f_{t}}{P_{t-1}}}\\&=1-{\frac {P_{t}}{P_{t-1}}}\end{aligned}}$ Полем (D) появляется ключевая связь между σ ²_P, и F. Q Во-первых... ^{[ 13 ]} ${\begin{aligned}f_{t}&=1-\left(1-1\Delta f\right)^{t}\left(1-f_{0}\right)\end{aligned}}$ Во-вторых, предполагая, что F ₀ = 0 , правая сторона этого уравнения сводится к разделу в скобках уравнения (2) в конце последнего подраздела. То есть, если изначально нет инбридинга, ${\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}$ ! Кроме того, если это переставляется, ${\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}$ Полем То есть, когда начальное инбридинг равен нулю, две основные точки зрения биномиальной выборки гамета (генетический дрейф) непосредственно взаимосвязаны.

Самоотверждение в случайном удобрении

Легко упустить из виду это случайное оплодотворение включает в себя самоопределение. Sewall Wright показал, что доля 1/n случайных оплодотворение на самом деле является самочувствием. $\left(\bigotimes \right)$ , с оставшимся (N-1)/N, является поперечным оплодотворением $\left({\mathsf {X}}\right)$ Полем Следуя анализу и упрощению пути, было обнаружено, что новое представление случайного оплодотворения было обнаружено: ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ . ^{[ 27 ]}^{[ 37 ]} После дальнейшей перестройки были подтверждены более ранние результаты биномиальной выборки, а также некоторые новые меры. Два из них были потенциально очень полезны, а именно: (а) ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ ; и (б) ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$ .

Признание того, что самооценка может быть частью случайного оплодотворения, приводит к некоторым вопросам использования предыдущего случайного оплодотворения «коэффициента инбридинга». Очевидно, что это неуместно для любого вида, неспособных к самочувствительности , который включает в себя растения с механизмом самообеспекаемости, диологическими растениями и бисексуальными животными . Уравнение Райта было изменено позже, чтобы обеспечить версию случайного оплодотворения, которая включала только поперечное оплодотворение без самостоятельного оплодотворения . Пропорция 1/n ранее из-за самоопыления, теперь определяла инбридинги для дрейфов генов переноса, возникающее в результате предыдущего цикла. Новая версия: ^{[ 13 ]}^: 166 $f_{{\mathsf {X}}_{t}}=f_{t-1}+\Delta f\left(1+f_{t-2}-2f_{t-1}\right)$ .

справа изображают различия между стандартным случайным РФ и случайным оплодотворением, адаптированным для «поперечного оплодотворения только» CF. Графики Как видно, проблема нетривиальна для небольших размеров выборки Gamodeme.

Теперь необходимо отметить, что не только «панмиксия» не синоним для «случайного оплодотворения», но и «случайное оплодотворение» не является синонимом «поперечного оплодотворения».

Гомозиготность и гетерозиготность

В подразделе «Выборочные гамодейы-генетический дрейф» следуют серию выборки гамета, результатом которого было увеличение гомозиготности за счет гетерозиготности. С этой точки зрения рост гомозиготности был вызван выборками гамета. Уровни гомозиготности можно просматривать также в зависимости от того, возникают ли гомозиготы аллозигно или аутозигульно. Напомним, что аутозиготные аллели имеют одно и то же аллельное происхождение, вероятность (частота), из которого является коэффициент инбридинга ( F ) по определению. доля, возникающая аллюзигно, Поэтому составляет (1-F) . Для гамет , которые присутствуют с общей частотой P , следовательно, общая частота тех, которые являются аутозиготными, составляют ( F P ). Точно так же для гаметов -аутозиготной частоты ( F Q ). ^{[ 38 ]} Эти две точки зрения, касающиеся частот генотипа, должны быть подключены для установления согласованности.

Следуя сначала с точки зрения Auto/Allo , рассмотрите аллозиготный компонент. Это происходит с частотой (1-F) , и аллели объединяются в соответствии со случайным оплодотворением квадратичного расширения. Таким образом: $\left(1-f\right)\left[p_{0}+q_{0}\right]^{2}=\left(1-f\right)\left[p_{0}^{2}+q_{0}^{2}\right]+\left(1-f\right)\left[2p_{0}q_{0}\right]$ Рассмотрим следующий аутозиготный компонент. Поскольку эти аллели являются аутозиготными , они эффективно самостираются и производят генотипы AA или AA , но не гетерозиготы. Поэтому они производят ${\textstyle fp_{0}}$ "AA" Homozygotes Plus ${\textstyle fq_{0}}$ «Аа» гомозиготы. Добавление этих двух компонентов вместе приводит к: ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ для гомозиготы АА ; ${\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}$ для гомозиготы АА ; и ${\textstyle \left(1-f\right)2p_{0}q_{0}}$ Для гетерозиготы АА . ^{[ 13 ]}^: 65^{[ 14 ]} Это то же уравнение, которое представлено ранее в разделе «Само удобрение - альтернатива». Причина снижения гетерозиготности здесь ясно. Гетерозиготы могут возникнуть только из аллозиготного компонента, а его частота в объеме образца составляет просто (1-F) : следовательно, это также должен быть фактором, контролирующим частоту гетерозигот.

Во-вторых, точка зрения отбора проб пересмотрена. Ранее было отмечено, что снижение гетерозигот было ${\textstyle f\left(2p_{0}q_{0}\right)}$ Полем Это снижение распределяется одинаково по каждой гомозиготе; и добавляется к их основным ожиданиям случайного оплодотворения . Следовательно, частоты генотипа: ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ для гомозиготы "АА" ; ${\textstyle \left(q_{0}^{2}+fp_{0}q_{0}\right)}$ для гомозиготы "АА" ; и ${\textstyle 2p_{0}q_{0}-f\left(2p_{0}q_{0}\right)}$ для гетерозиготы.

В -третьих, согласованность между двумя предыдущими потребностями точек зрения. Очевидно [из соответствующих уравнений выше], что гетерозиготная частота одинакова в обеих точках зрения. Однако такой простой результат не сразу очевиден для гомозигот. Начните с рассмотрения окончательного уравнения AA Homozygote в параграфе Auto/Allo выше:- ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ Полем Расширьте кронштейны и следуйте за повторным сбором [в рамках полученных] двух новых терминов с общим фактором F в них. Результат: ${\textstyle p_{0}^{2}-f\left(p_{0}^{2}-p_{0}\right)}$ Полем Далее, для скобок " P ²₀ ", a (1-q) заменяется P , результат становится ${\textstyle p_{0}^{2}-f\left[p_{0}\left(1-q_{0}\right)-p_{0}\right]}$ Полем После этой замены это простой вопрос умножения, упрощения и просмотра знаков. Конечный результат ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ , что является именно результатом для АА в абзаце отбора проб . Следовательно, две точки зрения последовательны для гомозиготы АА . последовательность точек зрения АА Аналогичным образом, также может быть показана . Две точки зрения последовательны для всех классов генотипов.

Расширенные принципы

Другие модели оплодотворения

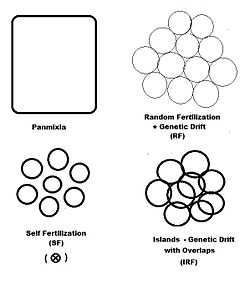
В предыдущих разделах дисперсивное случайное оплодотворение ( генетическое дрейф ) рассматривалось всесторонне, а самоотверженность и гибридизация были исследованы в различной степени. Диаграмма слева изображает первые два из них, а также еще один «пространственно основанный» с шаблоном: острова . Это шаблон случайного оплодотворения с диспергированными гамодом , с добавлением «перекрытий», в которых происходит недисперсивное случайное оплодотворение. С моделью островов отдельные размеры Gamodeme ( 2N ) наблюдаются, а перекрытия ( M ) минимальны. Это один из возможностей Sewall Wright. ^{[ 37 ]} В дополнение к «пространственно» моделям оплодотворения, есть и другие, основанные либо на «фенотипических» или «отношениях». Фенотипические ассортирующее основания включают оплодотворение (между аналогичными фенотипами) и диссокартовое оплодотворение (между противоположными фенотипами). Паттерны отношений включают в себя пересечение SIB , пересечение кузена и спину - и рассматриваются в отдельном разделе. Самословие может рассматриваться как с точки зрения пространственной, так и с точки зрения взаимоотношений.

«Острова» случайное оплодотворение

Разведчивающая популяция состоит из небольших выборки рассеянных случайных оплодотворяющих гамдом размера ${\textstyle 2N_{k}}$ ( k = 1 ... s ) с « перекрытиями » пропорции ${\textstyle m_{k}}$ в котором происходит недисперсивное случайное оплодотворение . Дисперсионная доля , таким образом ${\textstyle \left(1-m_{k}\right)}$ Полем Обычная популяция состоит из взвешенных средних размеров выборки, частот аллеля и генотипов и средних потомков, как это было сделано для генетического дрейфа в более раннем разделе. Тем не менее, каждый размер выборки гамета уменьшается, чтобы обеспечить перекрытие , тем самым найти ${\textstyle 2N_{k}}$ эффективно для ${\textstyle \left(1-m_{k}\right)}$ .

Для краткости аргумент дополнится с опущенными подписками. Вспомните это ${\textstyle {\tfrac {1}{2N}}}$ является ${\textstyle \Delta f}$ в общем. [Здесь, и после, 2N относится к ранее определенному размеру выборки, а не к какой -либо «скорректированной» версии островов.]

После упрощения, ^{[ 37 ]} $^{\mathsf {islands}}\Delta f={\frac {\left(1-m\right)^{2}}{2N-m^{2}\left(2N-1\right)}}$ Обратите внимание, что когда m = 0 это уменьшается до предыдущего Δ f . Взаимное из этого предоставляет оценку " ${\textstyle 2N_{k}}$ эффективно для ${\textstyle \left(1-m_{k}\right)}$ ", упомянутое выше.

Этот ΔF также заменяется в предыдущий коэффициент инбридинга , чтобы получить ^{[ 37 ]} ${^{\mathsf {islands}}f_{t}}=\ {^{\mathsf {islands}}\Delta f_{t}}+\left(1-\ {^{\mathsf {islands}}\Delta f_{t}}\right)\ {^{\mathsf {islands}}f_{t-1}}$ где t является индексом в течение поколений, как и прежде.

Эффективная пропорция перекрытия также может быть получена, также можно получить, ^{[ 37 ]} как $m_{t}=1-\left[{\frac {2N\ {^{\mathsf {islands}}\Delta f_{t}}}{\left(2N-1\right)\ {^{\mathsf {islands}}\Delta f_{t}+1}}}\right]^{\tfrac {1}{2}}$

Графики справа показывают инбридинг для размера гамодемоя 2n = 50 для обычного дисперсного случайного оплодотворения (RF) (M = 0) и для M = 0,0625, 0,125, 0,25, 0,5 четырех уровней перекрытия ( ) Полем В результате инбридинга действительно наблюдалось снижение недисперсного случайного оплодотворения в перекрытиях. Это особенно примечательно, как M → 0,50 . Sewall Wright предположил, что это значение должно быть ограничением для использования этого подхода. ^{[ 37 ]}

Аллель -перетасовка - замена аллеля

Ген -модель исследует путь наследия с точки зрения «входов» (аллели/гаметы) и «выходы» (генотипы/зиготы), причем оплодотворение является «процессом», конвертирующим один в другой. Альтернативная точка зрения концентрируется на самом «процессе» и рассматривает генотипы Zygote, возникающие в результате перетасовки аллеля. В частности, он рассматривает результаты, как если бы один аллель был «заменен» на другого во время перетасовки, вместе с остатком, который отклоняется от этой точки зрения. Это сформировало неотъемлемую часть метода Фишера, ^{[ 8 ]} В дополнение к использованию частот и эффектов для создания его генетической статистики. ^{[ 14 ]} Дискурсивный вывод альтернативы замены аллеля следует. ^{[ 14 ]}^: 113

Предположим, что обычное случайное оплодотворение гаметов в «базовой» газодемоме - сдерживании P Gametes ( A и Q Gametes ( A ) - заменяется оплодотворением на «наводнение» гамет, содержащих единый аллель ( A или , ) но не оба). Зиготические результаты могут быть интерпретированы с точки зрения того, что аллель «наводнения», заменяющий «альтернативный аллель в базовой» Gamodeme. Диаграмма помогает следовать этой точке зрения: верхняя часть изображает замену , в то время как нижняя часть показывает замену . («RF -аллель» диаграмма - это аллель в «базовой» газодемоме.)

Рассмотрим верхнюю часть сначала. Поскольку базовая A присутствует с частотой P , заменитель что оплодотворяет его с частотой P, приводит к Zygote AA эффектом аллеля A. с Таким образом, его вклад в результат является продукт ${\textstyle \left(p\ a\right)}$ Полем Точно так же, когда заменитель оплодотворяет основание A (что приводит к АА с частотой Q и гетерозиготного эффекта D ), вклад ${\textstyle \left(q\ d\right)}$ Полем общий результат замены A IS IS Поэтому ${\textstyle \left(p\ a+q\ d\right)}$ Полем В настоящее время это ориентировано на среднее население [см. Ранее раздел], выражая его как отклонение от этого среднего: ${\textstyle \left(p\ a+q\ d\right)-G}$

После некоторого алгебраического упрощения это становится $\beta _{A}=q\ \left[a+\left(q-p\right)d\right]$ - замены а . Эффект

Параллельные рассуждения могут быть применены к нижней части диаграммы, заботясь о различиях в частотах и эффектах генов. Результатом является эффект замены A , который $\beta _{a}=-\ p\left[a+\left(q-p\right)d\right]$ Общим фактором внутри скобков является средний эффект замены аллеля , ^{[ 14 ]}^: 113 и есть $\beta =a+\left(q-p\right)d$ Это также может быть получено более прямым образом, но результат такой же. ^{[ 39 ]}

В последующих разделах эти эффекты замещения помогают определить генотипы генной модели как, состоящие из разделения, предсказанного этими новыми эффектами ( замещения ожидания ), и остаточных ( отклонений для замены ) между этими ожиданиями и предыдущими эффектами генной модели. Ожидания , также называются ценностями размножения а отклонения также называются отклонениями доминирования .

В конечном счете, дисперсия, возникающая в результате ожиданий замены, становится так называемой аддитивной генетической дисперсией (σ (σ ²_А ) ^{[ 14 ]} (Также геновая дисперсия ^{[ 40 ]})-в то время как это, возникающее в результате отклонений замещения, становится так называемой дисперсией доминирования (σ ²_Г ) . Примечательно, что ни один из этих терминов не отражает истинные значения этих дисперсий. «Генеральная дисперсия » менее сомнительна, чем аддитивная генетическая дисперсия , и больше в соответствии с собственным именем Фишера для этого раздела. ^{[ 8 ]}^{[ 29 ]}^: 33 Менее изменчивое имя для дисперсии отклонения доминирования- « дисперсия квази-доминантности» [см. Следующие разделы для дальнейшего обсуждения]. Эти последние термины предпочтительнее здесь.

Эффекты генов переопределены

Эффекты генной модели ( A , D и -a ) вскоре важны при получении отклонений от замещения , которые впервые обсуждались в предыдущем разделе замещения аллелей . Тем не менее, они должны быть пересмотрены, прежде чем они станут полезными в этом упражнении. Во-первых, они должны быть повторно центролизованы вокруг среднего значения популяции ( G ), и, во-вторых, их необходимо переоценить как функции β , средний эффект замещения аллелей .

Сначала рассмотрим повторную централизацию. Регентрализованный эффект для АА- это • = a- g , который после упрощения становится • = 2 Q (a- p d) . Аналогичный эффект для AA - d • = d - g = a ( q - p ) + d (1-2 pq ) , после упрощения. Наконец, повторный центр-эффект для AA составляет (-a) • = -2 p (a+ q d) . ^{[ 14 ]}^{: 116–119}

Во-вторых, рассмотрим повторный прибор этих повторных централизованных эффектов как функций β . Вспоминая из секции «замены аллеля», который β = [a +(qp) d], перестройка дает = [β -(qp) d] . После замены этого на a in a • и упрощение окончательная версия становится •• = 2q (β-qd) . Точно так же D • становится d •• = β (qp) + 2pqd ; и (-a) • становится (-a) •• = -2p (β+pd) . ^{[ 14 ]}^: 118

Замена генотипа - ожидания и отклонения

Генотипы Zygote являются мишенью для всего этого препарата. Гомозиготный генотип AA - это объединение двух эффектов замещения A , по одному от каждого пола. его Следовательно, ожидание замены составляет β _AA = 2β _A = 2 Q β (см. Предыдущие разделы). Аналогичным образом, ожидание замены AA A составляет β _AA = β ₊ β _A = ( Q - P ) β ; и для AA , β _AA = 2β _A = -2 P β . Эти ожидания замены генотипов также называются ценностями размножения . ^{[ 14 ]}^{: 114–116}

Отклонения для замены -это различия между этими ожиданиями и эффектами генов после их двухэтапного переопределения в предыдущем разделе. Следовательно, d _aa = a •• - β _aa = -2 q ²D после упрощения. Точно так же d _aa = d •• - β _aa = 2 pq d после упрощения. Наконец, d _aa = (-a) •• -β _aa = -2 p ²D после упрощения. ^{[ 14 ]}^{: 116–119} Обратите внимание, что все эти отклонения замены в конечном итоге являются функциями генового эффекта D , что объясняет использование [«D» плюс индекс] в качестве их символов. Тем не менее, в логике является серьезный нечистич , чтобы рассматривать их как учитывание доминирования (гетерозигоза) во всей модели гена: они просто являются функциями «D», а не аудит «D» в системе. Они столь же получены: отклонения от ожиданий замены !

«Ожидания замены» в конечном итоге приводят к σ ²_A (так называемая «аддитивная» генетическая дисперсия); и «отклонения замены» вызывают σ ²_D (так называемая генетическая дисперсия «доминирования»). Помните, однако, что средний эффект замещения (β) также содержит «D» [см. Предыдущие разделы], указывая на то, что доминирование также встроено в дисперсию «аддитивной» [см. Следующие разделы о генотипической дисперсии для их производных]. Помните также [см. Предыдущий абзац], что «отклонения замены» не учитывают доминирование в системе (быть не более чем отклонениями от ожиданий замещения ), но которые, как оказалось, состоят из алгебраически функций «D». Более подходящие имена для этих соответствующих дисперсий могут быть σ ²_B (дисперсия «размножения») и σ ²_δ (дисперсия «размножения»). Однако, как отмечалось ранее, «генический» (σ ²_А ) и «квази-доминирование» (σ ²_Г ), соответственно, будет предпочтительнее здесь.

Генотипическая дисперсия

Есть два основных подхода к определению и разделению генотипической дисперсии . Один основан на эффектах генной модели , ^{[ 40 ]} в то время как другой основан на эффектах замены генотипа ^{[ 14 ]} They are algebraically inter-convertible with each other.^[36] основное происхождение случайного оплодотворения В этом разделе рассматривается с эффектами инбридинга и дисперсии. Это рассматривается позже, чтобы получить более общее решение. До тех пор, пока это моногеновое лечение не будет заменено многопользовательским , и до тех пор, пока эпистаз не будет разрешен в свете результатов эпигенетики , генотипическая дисперсия имеет только компоненты, рассматриваемые здесь.

Gene-model approach – Mather Jinks Hayman

It is convenient to follow the biometrical approach, which is based on correcting the unadjusted sum of squares (USS) by subtracting the correction factor (CF). Because all effects have been examined through frequencies, the USS can be obtained as the sum of the products of each genotype's frequency' and the square of its gene-effect. The CF in this case is the mean squared. The result is the SS, which, again because of the use of frequencies, is also immediately the variance.^[9]

The ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ , and the ${\textstyle {\mathsf {CF}}={\mathsf {G}}^{2}}$ . The ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$

After partial simplification, ${\begin{aligned}\sigma _{G}^{2}&=2pqa^{2}+(q-p)4pqad+2pqd^{2}+(2pq)^{2}d^{2}\\&=\sigma _{a}^{2}+({\text{weighted-covariance}})_{ad}+\sigma _{d}^{2}+\sigma _{D}^{2}\\&={\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{1}+{\tfrac {1}{4}}{\mathsf {H}}_{2}\end{aligned}}$ The last line is in Mather's terminology.^[40]^: 212^[41]^[42]

Here, σ²_a is the homozygote or allelic variance, and σ²_d is the heterozygote or dominance variance. The substitution deviations variance (σ²_D) is also present. The (weighted_covariance)_ad^[43] is abbreviated hereafter to " cov_ad ".

These components are plotted across all values of p in the accompanying figure. Notice that cov_ad is negative for p > 0.5.

Most of these components are affected by the change of central focus from homozygote mid-point (mp) to population mean (G), the latter being the basis of the Correction Factor. The cov_ad and substitution deviation variances are simply artifacts of this shift. The allelic and dominance variances are genuine genetical partitions of the original gene-model, and are the only eu-genetical components. Even then, the algebraic formula for the allelic variance is effected by the presence of G: it is only the dominance variance (i.e. σ²_d ) which is unaffected by the shift from mp to G.^[36] These insights are commonly not appreciated.

Further gathering of terms [in Mather format] leads to ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ , where ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ . It is useful later in Diallel analysis, which is an experimental design for estimating these genetical statistics.^[44]

If, following the last-given rearrangements, the first three terms are amalgamated together, rearranged further and simplified, the result is the variance of the Fisherian substitution expectation.

That is: $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$

Notice particularly that σ²_A is not σ²_a. The first is the substitution expectations variance, while the second is the allelic variance.^[45] Notice also that σ²_D (the substitution-deviations variance) is not σ²_d (the dominance variance), and recall that it is an artifact arising from the use of G for the Correction Factor. [See the "blue paragraph" above.] It now will be referred to as the "quasi-dominance" variance.

Also note that σ²_D < σ²_d ("2pq" being always a fraction); and note that (1) σ²_D = 2pq σ²_d, and that (2) σ²_d = σ²_D / (2pq). That is: it is confirmed that σ²_D does not quantify the dominance variance in the model. It is σ²_d which does that. However, the dominance variance (σ²_d) can be estimated readily from the σ²_D if 2pq is available.

From the Figure, these results can be visualized as accumulating σ²_a, σ²_d and cov_ad to obtain σ²_A, while leaving the σ²_D still separated. It is clear also in the Figure that σ²_D < σ²_d, as expected from the equations.

The overall result (in Fisher's format) is ${\begin{aligned}\sigma _{G}^{2}&=2pq\left[a+(q-p)d\right]^{2}+\left(2pq\right)^{2}d^{2}\\&=\sigma _{A}^{2}+\sigma _{D}^{2}\\&=\left[\left(\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}\right)\right]+\left[2pq\ \sigma _{d}^{2}\right]\end{aligned}}$ The Fisherian components have just been derived, but their derivation via the substitution effects themselves is given also, in the next section.

Allele-substitution approach – Fisher

Reference to the several earlier sections on allele substitution reveals that the two ultimate effects are genotype substitution expectations and genotype substitution deviations. Notice that these are each already defined as deviations from the random fertilization population mean (G). For each genotype in turn therefore, the product of the frequency and the square of the relevant effect is obtained, and these are accumulated to obtain directly a SS and σ².^[46] Details follow.

σ²_A = p² β_AA² + 2pq β_Aa² + q² β_aa², which simplifies to σ²_A = 2pqβ²—the Genic variance.

σ²_D = p² d_AA² + 2pq d_Aa² + q d_aa², which simplifies to σ²_D = (2pq)² d²—the quasi-Dominance variance.

Upon accumulating these results, σ²_G = σ²_A + σ²_D . These components are visualized in the graphs to the right. The average allele substitution effect is graphed also, but the symbol is "α" (as is common in the citations) rather than "β" (as is used herein).

Once again, however, refer to the earlier discussions about the true meanings and identities of these components. Fisher himself did not use these modern terms for his components. The substitution expectations variance he named the "genetic" variance; and the substitution deviations variance he regarded simply as the unnamed residual between the "genotypic" variance (his name for it) and his "genetic" variance.^[8]^[29]^: 33^[47]^[48] [The terminology and derivation used in this article are completely in accord with Fisher's own.] Mather's term for the expectations variance—"genic"^[40]—is obviously derived from Fisher's term, and avoids using "genetic" (which has become too generalized in usage to be of value in the present context). The origin is obscure of the modern misleading terms "additive" and "dominance" variances.

Note that this allele-substitution approach defined the components separately, and then totaled them to obtain the final Genotypic variance. Conversely, the gene-model approach derived the whole situation (components and total) as one exercise. Bonuses arising from this were (a) the revelations about the real structure of σ²_A, and (b) the real meanings and relative sizes of σ²_d and σ²_D (see previous sub-section). It is also apparent that a "Mather" analysis is more informative, and that a "Fisher" analysis can always be constructed from it. The opposite conversion is not possible, however, because information about cov_ad would be missing.

Dispersion and the genotypic variance

In the section on genetic drift, and in other sections that discuss inbreeding, a major outcome from allele frequency sampling has been the dispersion of progeny means. This collection of means has its own average, and also has a variance: the amongst-line variance. (This is a variance of the attribute itself, not of allele frequencies.) As dispersion develops further over succeeding generations, this amongst-line variance would be expected to increase. Conversely, as homozygosity rises, the within-lines variance would be expected to decrease. The question arises therefore as to whether the total variance is changing—and, if so, in what direction. To date, these issues have been presented in terms of the genic (σ ²_A ) and quasi-dominance (σ ²_D ) variances rather than the gene-model components. This will be done herein as well.

The crucial overview equation comes from Sewall Wright,^[13] ^{: 99, 130}^[37] and is the outline of the inbred genotypic variance based on a weighted average of its extremes, the weights being quadratic with respect to the inbreeding coefficient ${\textstyle f}$ . This equation is:

$\sigma _{G_{f}}^{2}=\left(1-f\right)\sigma _{G_{0}}^{2}+f\ \sigma _{G_{1}}^{2}+f\left(1-f\right)\left[G_{0}-G_{1}\right]^{2}$

where ${\textstyle f}$ is the inbreeding coefficient, ${\textstyle \sigma _{G_{0}}^{2}}$ is the genotypic variance at f=0, ${\textstyle \sigma _{G_{1}}^{2}}$ is the genotypic variance at f=1, ${\textstyle G_{0}}$ is the population mean at f=0, and ${\textstyle G_{1}}$ is the population mean at f=1.

The ${\textstyle \left(1-f\right)}$ component [in the equation above] outlines the reduction of variance within progeny lines. The ${\textstyle f}$ component addresses the increase in variance amongst progeny lines. Lastly, the ${\textstyle f\left(1-f\right)}$ component is seen (in the next line) to address the quasi-dominance variance.^[13] ^{: 99 & 130} These components can be expanded further thereby revealing additional insight. Thus:-

$\sigma _{G_{f}}^{2}=\left(1-f\right)\left[\sigma _{A_{0}}^{2}+\sigma _{D_{0}}^{2}\right]+f\ \left(4pq\ a^{2}\right)+f\ \left(1-f\right)\left[2pq\ d\right]^{2}$

Firstly, σ²_G(0) [in the equation above] has been expanded to show its two sub-components [see section on "Genotypic variance"]. Next, the σ²_G(1) has been converted to 4pqa² , and is derived in a section following. The third component's substitution is the difference between the two "inbreeding extremes" of the population mean [see section on the "Population Mean"].^[36]

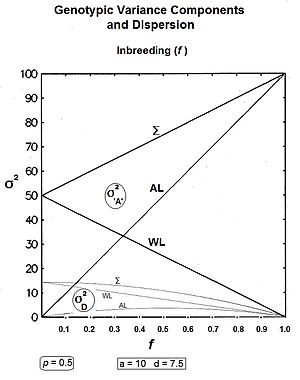
Dispersion and components of the genotypic variance

Summarising: the within-line components are ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ and ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ ; and the amongst-line components are ${\textstyle 2f\ \sigma _{a_{0}}^{2}}$ and ${\textstyle \left(f-f^{2}\right)\sigma _{D_{0}}^{2}}$ .^[36]

Rearranging gives the following: ${\begin{aligned}\sigma _{A_{inbred}}^{2}&=\left(1-f\right)\sigma _{A_{0}}^{2}+2f\sigma _{a_{0}}^{2}\\&=\left(1+f\right)\sigma _{A_{f}}^{2}\end{aligned}}$ The version in the last line is discussed further in a subsequent section.

Similarly, ${\begin{aligned}\sigma _{D_{inbred}}^{2}&=\left(1-f\right)\sigma _{D_{0}}^{2}+\left(f-f^{2}\right)\sigma _{D_{0}}^{2}\\&=\left(1-f^{2}\right)\sigma _{D_{0}}^{2}\end{aligned}}$

Graphs to the left show these three genic variances, together with the three quasi-dominance variances, across all values of f, for p = 0.5 (at which the quasi-dominance variance is at a maximum). Graphs to the right show the Genotypic variance partitions (being the sums of the respective genic and quasi-dominance partitions) changing over ten generations with an example f = 0.10.

Answering, firstly, the questions posed at the beginning about the total variances [the Σ in the graphs] : the genic variance rises linearly with the inbreeding coefficient, maximizing at twice its starting level. The quasi-dominance variance declines at the rate of (1 − f² ) until it finishes at zero. At low levels of f, the decline is very gradual, but it accelerates with higher levels of f.

Secondly, notice the other trends. It is probably intuitive that the within line variances decline to zero with continued inbreeding, and this is seen to be the case (both at the same linear rate (1-f) ). The amongst line variances both increase with inbreeding up to f = 0.5, the genic variance at the rate of 2f, and the quasi-dominance variance at the rate of (f − f²). At f > 0.5, however, the trends change. The amongst line genic variance continues its linear increase until it equals the total genic variance. But, the amongst line quasi-dominance variance now declines towards zero, because (f − f²) also declines with f > 0.5.^[36]

Derivation of σ²_G(1)

Recall that when f=1, heterozygosity is zero, within-line variance is zero, and all genotypic variance is thus amongst-line variance and deplete of dominance variance. In other words, σ²_G(1) is the variance amongst fully inbred line means. Recall further [from "The mean after self-fertilization" section] that such means (G₁'s, in fact) are G = a(p-q). Substituting (1-q) for the p, gives G₁ = a (1 − 2q) = a − 2aq.^[14]^: 265 Therefore, the σ²_G(1) is the σ²_(a-2aq) actually. Now, in general, the variance of a difference (x-y) is [ σ²_x + σ²_y − 2 cov_xy ].^[49]^: 100^[50] ^: 232 Therefore, σ²_G(1) = [ σ²_a + σ²_2aq − 2 cov_{(a, 2aq)} ] . But a (an allele effect) and q (an allele frequency) are independent—so this covariance is zero. Furthermore, a is a constant from one line to the next, so σ²_a is also zero. Further, 2a is another constant (k), so the σ²_2aq is of the type σ²_{k X}. In general, the variance σ²_{k X} is equal to k² σ²_X .^[50]^: 232 Putting all this together reveals that σ²_(a-2aq) = (2a)² σ²_q . Recall [from the section on "Continued genetic drift"] that σ²_q = pq f . With f=1 here within this present derivation, this becomes pq 1 (that is pq), and this is substituted into the previous.

The final result is: σ²_G(1) = σ²_(a-2aq) = 4a² pq = 2(2pq a²) = 2 σ²_a .

It follows immediately that f σ²_G(1) = f 2 σ²_a . [This last f comes from the initial Sewall Wright equation : it is not the f just set to "1" in the derivation concluded two lines above.]

Total dispersed genic variance – σ²_A(f) and β_f

Previous sections found that the within line genic variance is based upon the substitution-derived genic variance ( σ²_A )—but the amongst line genic variance is based upon the gene model allelic variance ( σ²_a ). These two cannot simply be added to get total genic variance. One approach in avoiding this problem was to re-visit the derivation of the average allele substitution effect, and to construct a version, ( β_f ), that incorporates the effects of the dispersion. Crow and Kimura achieved this^[13] ^{: 130–131} using the re-centered allele effects (a•, d•, (-a)• ) discussed previously ["Gene effects re-defined"]. However, this was found subsequently to under-estimate slightly the total Genic variance, and a new variance-based derivation led to a refined version.^[36]

The refined version is: β_f = { a² + [(1−f ) / (1 + f )] 2(q − p ) ad + [(1-f ) / (1 + f )] (q − p )² d² } ^(1/2)

Consequently, σ²_A(f) = (1 + f ) 2pq β_f ² does now agree with [ (1-f) σ²_A(0) + 2f σ²_a(0) ] exactly.

Total and partitioned dispersed quasi-dominance variances

The total genic variance is of intrinsic interest in its own right. But, prior to the refinements by Gordon,^[36] it had had another important use as well. There had been no extant estimators for the "dispersed" quasi-dominance. This had been estimated as the difference between Sewall Wright's inbred genotypic variance ^[37] and the total "dispersed" genic variance [see the previous sub-section]. An anomaly appeared, however, because the total quasi-dominance variance appeared to increase early in inbreeding despite the decline in heterozygosity.^[14] ^: 128 ^: 266

The refinements in the previous sub-section corrected this anomaly.^[36] At the same time, a direct solution for the total quasi-dominance variance was obtained, thus avoiding the need for the "subtraction" method of previous times. Furthermore, direct solutions for the amongst-line and within-line partitions of the quasi-dominance variance were obtained also, for the first time. [These have been presented in the section "Dispersion and the genotypic variance".]

Environmental variance

The environmental variance is phenotypic variability, which cannot be ascribed to genetics. This sounds simple, but the experimental design needed to separate the two needs very careful planning. Even the "external" environment can be divided into spatial and temporal components ("Sites" and "Years"); or into partitions such as "litter" or "family", and "culture" or "history". These components are very dependent upon the actual experimental model used to do the research. Such issues are very important when doing the research itself, but in this article on quantitative genetics this overview may suffice.

It is an appropriate place, however, for a summary:

Phenotypic variance = genotypic variances + environmental variances + genotype-environment interaction + experimental "error" variance

i.e., σ²_P = σ²_G + σ²_E + σ²_GE + σ²

or σ²_P = σ²_A + σ²_D + σ²_I + σ²_E + σ²_GE + σ²

after partitioning the genotypic variance (G) into component variances "genic" (A), "quasi-dominance" (D), and "epistatic" (I).^[51]

The environmental variance will appear in other sections, such as "Heritability" and "Correlated attributes".

Heritability and repeatability

The heritability of a trait is the proportion of the total (phenotypic) variance (σ² _P) that is attributable to genetic variance, whether it be the full genotypic variance, or some component of it. It quantifies the degree to which phenotypic variability is due to genetics: but the precise meaning depends upon which genetical variance partition is used in the numerator of the proportion.^[52] Research estimates of heritability have standard errors, just as have all estimated statistics.^[53]

Where the numerator variance is the whole Genotypic variance ( σ²_G ), the heritability is known as the "broadsense" heritability (H²). It quantifies the degree to which variability in an attribute is determined by genetics as a whole. ${\begin{aligned}H^{2}&={\frac {\sigma _{G}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\sigma _{A}^{2}+\sigma _{D}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\left[\sigma _{a}^{2}+\sigma _{d}^{2}+cov_{ad}\right]+\sigma _{D}^{2}}{\sigma _{P}^{2}}}\end{aligned}}$ [See section on the Genotypic variance.]

If only genic variance (σ²_A) is used in the numerator, the heritability may be called "narrow sense" (h²). It quantifies the extent to which phenotypic variance is determined by Fisher's substitution expectations variance. ${\begin{aligned}h^{2}&={\frac {\sigma _{A}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\sigma _{a}^{2}+\sigma _{d}^{2}+cov_{ad}}{\sigma _{P}^{2}}}\end{aligned}}$ Fisher proposed that this narrow-sense heritability might be appropriate in considering the results of natural selection, focusing as it does on change-ability, that is upon "adaptation".^[29] He proposed it with regard to quantifying Darwinian evolution.

Recalling that the allelic variance (σ ²_a) and the dominance variance (σ ²_d) are eu-genetic components of the gene-model [see section on the Genotypic variance], and that σ ²_D (the substitution deviations or "quasi-dominance" variance) and cov_ad are due to changing from the homozygote midpoint (mp) to the population mean (G), it can be seen that the real meanings of these heritabilities are obscure. The heritabilities ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ and ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ have unambiguous meaning.

Narrow-sense heritability has been used also for predicting generally the results of artificial selection. In the latter case, however, the broadsense heritability may be more appropriate, as the whole attribute is being altered: not just adaptive capacity. Generally, advance from selection is more rapid the higher the heritability. [See section on "Selection".] In animals, heritability of reproductive traits is typically low, while heritability of disease resistance and production are moderately low to moderate, and heritability of body conformation is high.

Repeatability (r²) is the proportion of phenotypic variance attributable to differences in repeated measures of the same subject, arising from later records. It is used particularly for long-lived species. This value can only be determined for traits that manifest multiple times in the organism's lifetime, such as adult body mass, metabolic rate or litter size. Individual birth mass, for example, would not have a repeatability value: but it would have a heritability value. Generally, but not always, repeatability indicates the upper level of the heritability.^[54]

r² = (s²_G + s²_PE)/s²_P

where s²_PE = phenotype-environment interaction = repeatability.

The above concept of repeatability is, however, problematic for traits that necessarily change greatly between measurements. For example, body mass increases greatly in many organisms between birth and adult-hood. Nonetheless, within a given age range (or life-cycle stage), repeated measures could be done, and repeatability would be meaningful within that stage.

Relationship

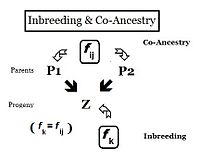
From the heredity perspective, relations are individuals that inherited genes from one or more common ancestors. Therefore, their "relationship" can be quantified on the basis of the probability that they each have inherited a copy of an allele from the common ancestor. In earlier sections, the Inbreeding coefficient has been defined as, "the probability that two same alleles ( A and A, or a and a ) have a common origin"—or, more formally, "The probability that two homologous alleles are autozygous." Previously, the emphasis was on an individual's likelihood of having two such alleles, and the coefficient was framed accordingly. It is obvious, however, that this probability of autozygosity for an individual must also be the probability that each of its two parents had this autozygous allele. In this re-focused form, the probability is called the co-ancestry coefficient for the two individuals i and j ( f _ij ). In this form, it can be used to quantify the relationship between two individuals, and may also be known as the coefficient of kinship or the consanguinity coefficient.^[13]^{: 132–143} ^[14]^: 82–92

Pedigree analysis

Pedigrees are diagrams of familial connections between individuals and their ancestors, and possibly between other members of the group that share genetical inheritance with them. They are relationship maps. A pedigree can be analyzed, therefore, to reveal coefficients of inbreeding and co-ancestry. Such pedigrees actually are informal depictions of path diagrams as used in path analysis, which was invented by Sewall Wright when he formulated his studies on inbreeding.^[55]^{: 266–298} Using the adjacent diagram, the probability that individuals "B" and "C" have received autozygous alleles from ancestor "A" is 1/2 (one out of the two diploid alleles). This is the "de novo" inbreeding (Δf_Ped) at this step. However, the other allele may have had "carry-over" autozygosity from previous generations, so the probability of this occurring is (de novo complement multiplied by the inbreeding of ancestor A ), that is (1 − Δf_Ped ) f_A = (1/2) f_A . Therefore, the total probability of autozygosity in B and C, following the bi-furcation of the pedigree, is the sum of these two components, namely (1/2) + (1/2)f_A = (1/2) (1+f _A ) . This can be viewed as the probability that two random gametes from ancestor A carry autozygous alleles, and in that context is called the coefficient of parentage ( f_AA ).^[13]^{: 132–143}^[14]^: 82–92 It appears often in the following paragraphs.

Following the "B" path, the probability that any autozygous allele is "passed on" to each successive parent is again (1/2) at each step (including the last one to the "target" X ). The overall probability of transfer down the "B path" is therefore (1/2)³ . The power that (1/2) is raised to can be viewed as "the number of intermediates in the path between A and X ", n_B = 3 . Similarly, for the "C path", n_C = 2 , and the "transfer probability" is (1/2)² . The combined probability of autozygous transfer from A to X is therefore [ f_AA (1/2)^(n_B) (1/2)^(n_C) ] . Recalling that f_AA = (1/2) (1+f _A ) , f_X = f_PQ = (1/2)^{(n_B + n_C + 1)} (1 + f_A ) . In this example, assuming that f_A = 0, f_X = 0.0156 (rounded) = f_PQ , one measure of the "relatedness" between P and Q.

In this section, powers of (1/2) were used to represent the "probability of autozygosity". Later, this same method will be used to represent the proportions of ancestral gene-pools which are inherited down a pedigree [the section on "Relatedness between relatives"].

Cross-multiplication rules

In the following sections on sib-crossing and similar topics, a number of "averaging rules" are useful. These derive from path analysis.^[55] The rules show that any co-ancestry coefficient can be obtained as the average of cross-over co-ancestries between appropriate grand-parental and parental combinations. Thus, referring to the adjacent diagram, Cross-multiplier 1 is that f_PQ = average of ( f_AC , f_AD , f_BC , f_BD ) = (1/4) [f_AC + f_AD + f_BC + f_BD ] = f_Y . In a similar fashion, cross-multiplier 2 states that f_PC = (1/2) [ f_AC + f_BC ]—while cross-multiplier 3 states that f_PD = (1/2) [ f_AD + f_BD ] . Returning to the first multiplier, it can now be seen also to be f_PQ = (1/2) [ f_PC + f_PD ], which, after substituting multipliers 2 and 3, resumes its original form.

In much of the following, the grand-parental generation is referred to as (t-2) , the parent generation as (t-1) , and the "target" generation as t.

Full-sib crossing (FS)

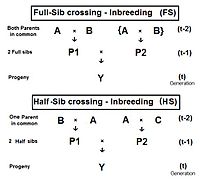
The diagram to the right shows that full sib crossing is a direct application of cross-Multiplier 1, with the slight modification that parents A and B repeat (in lieu of C and D) to indicate that individuals P1 and P2 have both of their parents in common—that is they are full siblings. Individual Y is the result of the crossing of two full siblings. Therefore, f_Y = f_P1,P2 = (1/4) [ f_AA + 2 f_AB + f_BB ] . Recall that f_AA and f_BB were defined earlier (in Pedigree analysis) as coefficients of parentage, equal to (1/2)[1+f_A ] and (1/2)[1+f_B ] respectively, in the present context. Recognize that, in this guise, the grandparents A and B represent generation (t-2) . Thus, assuming that in any one generation all levels of inbreeding are the same, these two coefficients of parentage each represent (1/2) [1 + f_(t-2) ] .

Now, examine f_AB . Recall that this also is f_P1 or f_P2 , and so represents their generation - f_(t-1) . Putting it all together, f_t = (1/4) [ 2 f_AA + 2 f_AB ] = (1/4) [ 1 + f_(t-2) + 2 f_(t-1) ] . That is the inbreeding coefficient for Full-Sib crossing .^[13]^{: 132–143}^[14]^: 82–92 The graph to the left shows the rate of this inbreeding over twenty repetitive generations. The "repetition" means that the progeny after cycle t become the crossing parents that generate cycle (t+1 ), and so on successively. The graphs also show the inbreeding for random fertilization 2N=20 for comparison. Recall that this inbreeding coefficient for progeny Y is also the co-ancestry coefficient for its parents, and so is a measure of the relatedness of the two Fill siblings.

Half-sib crossing (HS)

Derivation of the half sib crossing takes a slightly different path to that for Full sibs. In the adjacent diagram, the two half-sibs at generation (t-1) have only one parent in common—parent "A" at generation (t-2). The cross-multiplier 1 is used again, giving f_Y = f_(P1,P2) = (1/4) [ f_AA + f_AC + f_BA + f_BC ] . There is just one coefficient of parentage this time, but three co-ancestry coefficients at the (t-2) level (one of them—f_BC—being a "dummy" and not representing an actual individual in the (t-1) generation). As before, the coefficient of parentage is (1/2)[1+f_A ] , and the three co-ancestries each represent f_(t-1) . Recalling that f_A represents f_(t-2) , the final gathering and simplifying of terms gives f_Y = f_t = (1/8) [ 1 + f_(t-2) + 6 f_(t-1) ] .^[13]^{: 132–143}^[14]^: 82–92 The graphs at left include this half-sib (HS) inbreeding over twenty successive generations.

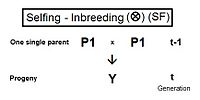
As before, this also quantifies the relatedness of the two half-sibs at generation (t-1) in its alternative form of f_{(P1, P2)} .

Self fertilization (SF)

A pedigree diagram for selfing is on the right. It is so straightforward it does not require any cross-multiplication rules. It employs just the basic juxtaposition of the inbreeding coefficient and its alternative the co-ancestry coefficient; followed by recognizing that, in this case, the latter is also a coefficient of parentage. Thus, f_Y = f_{(P1, P1)} = f_t = (1/2) [ 1 + f_(t-1) ] .^[13]^{: 132–143}^[14]^: 82–92 This is the fastest rate of inbreeding of all types, as can be seen in the graphs above. The selfing curve is, in fact, a graph of the coefficient of parentage.

Cousins crossings

These are derived with methods similar to those for siblings.^[13]^{: 132–143}^[14]^: 82–92 As before, the co-ancestry viewpoint of the inbreeding coefficient provides a measure of "relatedness" between the parents P1 and P2 in these cousin expressions.

The pedigree for First Cousins (FC) is given to the right. The prime equation is f_Y = f_t = f_P1,P2 = (1/4) [ f_1D + f₁₂ + f_CD + f_C2 ]. After substitution with corresponding inbreeding coefficients, gathering of terms and simplifying, this becomes f_t = (1/4) [ 3 f_(t-1) + (1/4) [2 f_(t-2) + f_(t-3) + 1 ]] , which is a version for iteration—useful for observing the general pattern, and for computer programming. A "final" version is f_t = (1/16) [ 12 f_(t-1) + 2 f_(t-2) + f_(t-3) + 1 ] .

The Second Cousins (SC) pedigree is on the left. Parents in the pedigree not related to the common Ancestor are indicated by numerals instead of letters. Here, the prime equation is f_Y = f_t = f_P1,P2 = (1/4) [ f_3F + f₃₄ + f_EF + f_E4 ]. After working through the appropriate algebra, this becomes f_t = (1/4) [ 3 f_(t-1) + (1/4) [3 f_(t-2) + (1/4) [2 f_(t-3) + f_(t-4) + 1 ]]] , which is the iteration version. A "final" version is f_t = (1/64) [ 48 f_(t-1) + 12 f_(t-2) + 2 f_(t-3) + f_(t-4) + 1 ] .

To visualize the pattern in full cousin equations, start the series with the full sib equation re-written in iteration form: f_t = (1/4)[2 f_(t-1) + f_(t-2) + 1 ]. Notice that this is the "essential plan" of the last term in each of the cousin iterative forms: with the small difference that the generation indices increment by "1" at each cousin "level". Now, define the cousin level as k = 1 (for First cousins), = 2 (for Second cousins), = 3 (for Third cousins), etc., etc.; and = 0 (for Full Sibs, which are "zero level cousins"). The last term can be written now as: (1/4) [ 2 f_(t-(1+k)) + f_(t-(2+k)) + 1] . Stacked in front of this last term are one or more iteration increments in the form (1/4) [ 3 f_(t-j) + ... , where j is the iteration index and takes values from 1 ... k over the successive iterations as needed. Putting all this together provides a general formula for all levels of full cousin possible, including Full Sibs. For kth level full cousins, f{k}_t = Ιter_{j = 1}^k { (1/4) [ 3 f_(t-j) + }_j + (1/4) [ 2 f_(t-(1+k)) + f_(t-(2+k)) + 1] . At the commencement of iteration, all f_(t-x) are set at "0", and each has its value substituted as it is calculated through the generations. The graphs to the right show the successive inbreeding for several levels of Full Cousins.

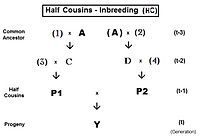
For first half-cousins (FHC), the pedigree is to the left. Notice there is just one common ancestor (individual A). Also, as for second cousins, parents not related to the common ancestor are indicated by numerals. Here, the prime equation is f_Y = f_t = f_P1,P2 = (1/4) [ f_3D + f₃₄ + f_CD + f_C4 ]. After working through the appropriate algebra, this becomes f_t = (1/4) [ 3 f_(t-1) + (1/8) [6 f_(t-2) + f_(t-3) + 1 ]] , which is the iteration version. A "final" version is f_t = (1/32) [ 24 f_(t-1) + 6 f_(t-2) + f_(t-3) + 1 ] . The iteration algorithm is similar to that for full cousins, except that the last term is (1/8) [ 6 f_(t-(1+k)) + f_(t-(2+k)) + 1 ] . Notice that this last term is basically similar to the half sib equation, in parallel to the pattern for full cousins and full sibs. In other words, half sibs are "zero level" half cousins.

There is a tendency to regard cousin crossing with a human-oriented point of view, possibly because of a wide interest in Genealogy. The use of pedigrees to derive the inbreeding perhaps reinforces this "Family History" view. However, such kinds of inter-crossing occur also in natural populations—especially those that are sedentary, or have a "breeding area" that they re-visit from season to season. The progeny-group of a harem with a dominant male, for example, may contain elements of sib-crossing, cousin crossing, and backcrossing, as well as genetic drift, especially of the "island" type. In addition to that, the occasional "outcross" adds an element of hybridization to the mix. It is not panmixia.

Backcrossing (BC)

Following the hybridizing between A and R, the F1 (individual B) is crossed back (BC1) to an original parent (R) to produce the BC1 generation (individual C). [It is usual to use the same label for the act of making the back-cross and for the generation produced by it. The act of back-crossing is here in italics. ] Parent R is the recurrent parent. Two successive backcrosses are depicted, with individual D being the BC2 generation. These generations have been given t indices also, as indicated. As before, f_D = f_t = f_CR = (1/2) [ f_RB + f_RR ] , using cross-multiplier 2 previously given. The f_RB just defined is the one that involves generation (t-1) with (t-2). However, there is another such f_RB contained wholly within generation (t-2) as well, and it is this one that is used now: as the co-ancestry of the parents of individual C in generation (t-1). As such, it is also the inbreeding coefficient of C, and hence is f_(t-1). The remaining f_RR is the coefficient of parentage of the recurrent parent, and so is (1/2) [1 + f_R ] . Putting all this together : f_t = (1/2) [ (1/2) [ 1 + f_R ] + f_(t-1) ] = (1/4) [ 1 + f_R + 2 f_(t-1) ] . The graphs at right illustrate Backcross inbreeding over twenty backcrosses for three different levels of (fixed) inbreeding in the Recurrent parent.

This routine is commonly used in Animal and Plant Breeding programmes. Often after making the hybrid (especially if individuals are short-lived), the recurrent parent needs separate "line breeding" for its maintenance as a future recurrent parent in the backcrossing. This maintenance may be through selfing, or through full-sib or half-sib crossing, or through restricted randomly fertilized populations, depending on the species' reproductive possibilities. Of course, this incremental rise in f_R carries-over into the f_t of the backcrossing. The result is a more gradual curve rising to the asymptotes than shown in the present graphs, because the f_R is not at a fixed level from the outset.

Contributions from ancestral genepools

In the section on "Pedigree analysis", ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ was used to represent probabilities of autozygous allele descent over n generations down branches of the pedigree. This formula arose because of the rules imposed by sexual reproduction: (i) two parents contributing virtually equal shares of autosomal genes, and (ii) successive dilution for each generation between the zygote and the "focus" level of parentage. These same rules apply also to any other viewpoint of descent in a two-sex reproductive system. One such is the proportion of any ancestral gene-pool (also known as 'germplasm') which is contained within any zygote's genotype.

Следовательно, доля наследственного генопула в генотипе составляет: $\gamma _{n}=\left({\frac {1}{2}}\right)^{n}$ where n = number of sexual generations between the zygote and the focus ancestor.

Например, каждый родитель определяет генопуль ${\textstyle \left({\tfrac {1}{2}}\right)^{1}}$ своему потомству; в то время как каждый прабабушка вносит свой вклад ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ к своему прайбусту.

Общий генопул Zygote ( γ ), конечно, является суммой сексуального вклада в его спуск.

${\begin{aligned}\Gamma &=\sum _{n=1}^{2^{n}}{\gamma _{n}}\\&=\sum _{n=1}^{2^{n}}{\left({\frac {1}{2}}\right)^{n}}\end{aligned}}$

Отношения с помощью наследственных генопул

Очевидно, что люди, произошедшие от общего предкового генопула. Это не означает, что они идентичны в своих генах (аллелях), потому что на каждом уровне предка, сегрегация и ассортимент произойдет при производстве гамет. Но они возникнут из того же пула аллелей, доступных для этих мейосов и последующих удобрений. [Сначала эта идея была встречена в разделах по анализу и отношениям родословного.] Поэтому вклад генопула [см. В разделе выше] их ближайшего общего предков генопул ( наследственный узел ) можно использовать для определения их отношений. Это приводит к интуитивному определению отношений, которое хорошо соответствует знакомым представлениям о «родстве», найденном в семейной истории; и позволяет сравнить «степень родства» для сложных моделей отношений, возникающих из -за такой генеалогии.

Единственные необходимые модификации (для каждого человека, по очереди), находятся в γ и связаны с переходом к «общему общему происхождению», а не с «индивидуальным общим происхождением». Для этого определите ρ (вместо γ ); m = количество предков в коммерке в узле (то есть только m = 1 или 2); и «индивидуальный индекс» k . Таким образом:

${\begin{aligned}\mathrm {P} _{k}&=\sum _{m=1}^{1,2}{\gamma _{n}}\\&=\sum _{m=1}^{1,2}{\left({\frac {1}{2}}\right)^{n}}\end{aligned}}$

Где, как и прежде, n = количество сексуальных поколений между индивидуумом и наследственным узлом.

Пример приведен двумя первыми полномупринятами. Их ближайший общий наследственный узел - их бабушка и дедушка, который породил двух их братьев и сестер, и у них общие бабушки и бабушки. [См. Раннее родословную.] Для этого случая m = 2 и n = 2 , поэтому для каждого из них

${\begin{aligned}\mathrm {P} _{k}&=\sum _{m=1}^{2}{\gamma _{2}}\\&=\sum _{m=1}^{2}{\left({\frac {1}{2}}\right)^{2}}\\&={\frac {1}{2}}\end{aligned}}$

В этом простом случае каждый двоюродный брат имеет численно одинаковый ρ.

Второй пример может быть между двумя полными двоюродными братьями, но один ( k = 1 ) имеет три поколения обратно в наследственный узел (n = 3), а другое ( k = 2 ) только два (n = 2) [то есть второй и первые отношения двоюродного брата]. Для обоих m = 2 (они полные двоюродные братья).

${\begin{aligned}\mathrm {P} _{1}&=\sum _{m=1}^{2}{\gamma _{3}}\\&=\sum _{m=1}^{2}{\left({\frac {1}{2}}\right)^{3}}\\&={\frac {1}{4}}\end{aligned}}$

и

${\begin{aligned}\mathrm {P} _{2}&=\sum _{m=1}^{2}{\gamma _{2}}\\&=\sum _{m=1}^{2}{\left({\frac {1}{2}}\right)^{2}}\\&={\frac {1}{2}}\end{aligned}}$

Обратите внимание, что каждый двоюродный брат имеет разные ρ _k .

GRC - коэффициент отношений с генопулом

В любой парной оценке отношений есть один ρ _k для каждого человека: он остается средним для их среднего, чтобы объединить их в один «коэффициент отношений». Поскольку каждый ρ - часть общего генопула , соответствующим средним для них является среднее геометрическое ^{[ 56 ]}^{[ 57 ]}^: 34–55 Это среднее значение является их коэффициентом отношений с генопулом - «GRC».

Для первого примера (два полных первых учреждения) их GRC = 0,5; Для второго случая (полный первый и второй двоюродный брат), их GRC = 0,3536.

Все эти отношения (GRC) являются применением анализа пути. ^{[ 55 ]}^{: 214–298} Сводка некоторых уровней отношений (GRC).

Гриль	Примеры отношений
1.00	Полные сибы
0.7071	Родитель ↔ потомство; Дядя/тетя ↔ племянник/племянница
0.5	Полные первые двоюродные братья; Половина сибов; Grand Parent ↔ Grand Offspring
0.3536	Полные двоюродные братья первой ↔ секунд; Полный первые двоюродные братья {1 удалить}
0.25	Полный второй двоюродные братья; половина первых двоюродных братьев; Полный первый двоюродные братья {2 удаляет}
0.1768	Полный первый двоюродный брат {3 удаляет}; Полный второй двоюродные братья {1 удалить}
0.125	Полные третьи двоюродные братья; полусекунды, двоюродные братья; Полный 1 -й двоюродные братья {4 удаляет}
0.0884	Полные первые кузены {5 удаляет}; половина секунды двоюродных братьев {1 удалить}
0.0625	Полный четвертый кузены; Половина третьих двоюродных братьев

Сходство между родственниками

Они аналогичны генотипическим отклонениям, могут быть получены либо через подход генной модели («Мазер»), либо подход аллеля-подключения («Фишер»). Здесь каждый метод демонстрируется для альтернативных случаев.

Родительская ковариация

Их можно рассматривать либо как ковариацию между любым потомством и любым из его родителей ( PO ), либо как ковариации между любым потомством и «средним родителем» обоих родителей ( MPO ).

Одно родителей и потомство (PO)

Это может быть получено как сумма перекрестных продуктов между родительскими генами и половиной ожиданий потомства с использованием подхода к аллеле-подключению. Половина ожидания потомства объясняет тот факт, что только один из двух родителей рассматривается . Следовательно, соответствующие геновые эффекты родительских генов представляют собой повторные эффекты генов второй стадии, используемые для определения генотипических различий ранее, то есть: a ″ = 2q (a-qd) и d ″ = (qp) a + 2pqd , а также (-a ) ″ = -2p (a + pd) [см. Раздел «Эффекты генов переопределены»]. Точно так же соответствующие эффекты потомства, поскольку ожидания-аллеле-подключение -это половина более ранних значений размножения , последнее: A _AA = 2QA и AA ₌ (QP) A а также AA _, = -2PA [см. Раздел о «Замена генотипа - ожидания и отклонения»].

Поскольку все эти эффекты уже определены как отклонение от среднего генотипического, сумма перекрестного продукта с использованием { генотипной частотой * родительского гена-эффекта * полусредственного значения } сразу же обеспечивает ковариацию между каким-либо одним родителем между любым одним из родителей. и его потомство. После тщательного сбора терминов и упрощения это становится COV (PO) _A = PQA ² = ⁠ 1/2 ⁠ s ²_А ^{[ 13 ]} ^{: 132–141}^{[ 14 ]} ^{: 134–147}

К сожалению, аллель-субстиционирование обычно упускаются из виду, но, тем не менее, они не «прекратили существовать»! Напомним, что эти отклонения: d _aa = -2q ² D и D _AA = 2PQ D , а также D _AA = -2P ² D [см. Раздел «Замена генотипа - ожидания и отклонения»]. Следовательно, сумма перекрестного продукта с использованием { частота Genotype * Parental Genefct * Half-Substitution-Deviations } также немедленно обеспечивает ковариации аллеля-подключения между любым родителем и его потомством. Еще раз, после тщательного сбора терминов и упрощения, это становится COV (PO) _d = 2p ²Q. ²дюймовый ² = ⁠ 1/2 ⁠ s ²_{Дюймовый}

Следовательно, следует, что: Cov (po) = Cov (po) _a + cov (po) _d = ⁠ 1/2 ⁠ s ²_А + ⁠ 1/2 ⁠ s ²_D , когда доминирование не упускается из виду!

Средний родитель и потомство (MPO)

Поскольку существует множество комбинаций родительских генотипов, существует много разных средних и потомства, которые нужно учитывать вместе с различными частотами получения каждого сопряжения родителей. Подход генной модели является наиболее целесообразным в этом случае. Следовательно, нескорректированная сумма поперечных продуктов (USCP) -используя все продукты { родительскую паровую частоту * среднего уровня-генового геноподзора * , скорректируется путем вычитания {общего генотипического среднего}}}}}}}}}}}}}} }}- ² как коррекционный коэффициент (CF) . После умножения всех различных комбинаций, тщательного сбора терминов, упрощения, учета и отмены, где это применимо, это становится:

(Mpo) = pq [a + (qp) d] ² = pq a ² = ⁠ 1/2 ⁠ s ²_А , без доминирования, не было упущено в этом случае, так как оно было использовано при определении а . ^{[ 13 ]} ^{: 132–141}^{[ 14 ]} ^{: 134–147}

Приложения (Parent-Offspring)

Наиболее очевидным применением является эксперимент, который содержит всех родителей и их потомство, с взаимными крестами или без него, предпочтительно воспроизводится без предвзятости, что позволяет оценить все соответствующие средства, дисперсии и ковариации, вместе со стандартными ошибками. Эти оценочные статистические данные могут затем использоваться для оценки генетических разногласий. Вдвое больше разницы между оценками двух форм (скорректированной) ковариации родительской просмотра дает оценку S ²_D ; и вдвое больше COV (MPO) оценок S ²_А С соответствующим экспериментальным дизайном и анализом, ^{[ 9 ]}^{[ 49 ]}^{[ 50 ]} Стандартные ошибки могут быть получены и для этой генетической статистики. Это основное ядро эксперимента, известного как Анализ Диалеля , версия Mather, Jinks и Hayman, о которой обсуждается в другом разделе.

Второе приложение включает в себя использование регрессионного анализа , который оценивает статистику, ординату (Y-оценка), производного (коэффициент регрессии) и постоянный (y-перевод) исчисления. ^{[ 9 ]}^{[ 49 ]}^{[ 58 ]}^{[ 59 ]} Коэффициент регрессии оценивает скорость изменения функции, прогнозирующей Y от X , на основе минимизации остатков между установленной кривой и наблюдаемыми данными (Minres). Ни один альтернативный метод оценки такой функции не удовлетворяет этому основному требованию Minres. В целом, коэффициент регрессии оценивается как отношение ковариации (xy) к дисперсии детерминатора (x) . На практике размер выборки обычно одинаков как для x, так и для Y, так что это может быть написано как SCP (xy) / SS (x) , где все термины были определены ранее. ^{[ 9 ]}^{[ 58 ]}^{[ 59 ]} В настоящем контексте родители рассматриваются как «определяющая переменная» (x), а потомство - как «определенную переменную» (Y), а коэффициент регрессии - как «функциональные отношения» (ß _PO ) между двумя. Принимая COV (MPO) = ⁠ 1/2 ⁠ s ²_A as cov (xy) и s ²_P / 2 (дисперсия среднего значения двух родителей-середины родителей) как s ²_X , видно, что β _mpo = [ ⁠ 1/2 ⁠ s ²_A ] / [ ⁠ 1/2 ⁠ s ²_P ] = h ² . ^{[ 60 ]} Далее, используя COV (PO) = [ ⁠ 1/2 ⁠ s ²_А + ⁠ 1/2 ⁠ s ²_D ] как COV (XY) и S ²_{Проходить}  ²_X , видно, что 2 ß _po = [2 (2 ( ⁠ 1/2 ⁠ s ²_А + ⁠ 1/2 ⁠ s ²_D )] / s ²_P = h ² .

Анализ эпистаза ранее был предпринят с помощью подхода к дисперсии взаимодействия типа S ²_Аа и с ²_AD , а также S ²_Дд . Это было интегрировано с этими нынешними ковариациями, чтобы предоставить оценки для дисперсий эпистаза. Тем не менее, результаты эпигенетики предполагают, что это может быть не подходящим способом определения эпистаза.

Братья и сестры ковариации

Ковариация между половинами-сестрами ( HS ) легко определяется с использованием методов-аллеле-подключения; Но, опять же, вклад доминирования исторически был опущен. Однако, как и в случае с ковариацией среднего возраста/потомства, ковариация между полными SIB ( FS ) требует подхода «комбинирования родителей», что требует использования метода скорректированной генной модели; и доминирующий вклад исторически не был упущен из виду. Превосходство производных генной модели здесь так же очевидно, как и для генотипических отклонений.

Полусвиды того же обычного родителя (HS)

Сумма поперечных продуктов {частота общего родителя * полупрофильная стоимость одной половины * полупрофильного значения любой другой полусвиды в той же группе общего родителя} сразу же предоставляет одну из необходимых Ковариации, поскольку используемые эффекты [ значения размножения , представляющие ожидания аллеля-подключения], уже определяются как отклоняющиеся от среднего генотипического [см. Раздел «Замена аллеля-ожидания и отклонения»]. После упрощения. это становится: COV (HS) _A = ⁠ 1/2 ⁠ PQ A ² = ⁠ 1/4 ²_А ^{[ 13 ]} ^{: 132–141}^{[ 14 ]} ^{: 134–147} Однако существуют также отклонений для замены , определяя сумму перекрестных продуц (частота общего родителя * полупробемоционирование одного полусвидного расстояния любого другого половину-сиба в этом же общем родителе. -Group} , которая в конечном итоге приводит к: COV (HS) _D = P ² Q. ² дюймовый ² = ⁠ 1/4 ²_{Дюймовый} Добавление двух компонентов дает:

(HS) = (HS) _A + Position (HS) _D = ⁠ 1/4 ²_А + ⁠ 1/4 ²_{Дюймовый}

Полные сибы (FS)

Как объясняется во введении, используется метод, аналогичный тому, который используется для ковариации среднего возраста/потомства. Следовательно, нескорректированная сумма поперечных продуктов (USCP) с использованием всех продуктов-{ частота родительской пары * квадрат среднего по потомству генотипов }-скорректируется путем вычитания {общего среднего генотипа} ² как коррекционный коэффициент (CF) . В этом случае умножение всех комбинаций, тщательного сбора терминов, упрощения, факторинга и повреждения очень длительно. Это в конечном итоге становится:

(Fs) = pq a ² + р ² Q. ² дюймовый ² = ⁠ 1/2 ⁠ s ²_А + ⁠ 1/4 ²_D , без доминирования не было упущено. ^{[ 13 ]} ^{: 132–141}^{[ 14 ]} ^{: 134–147}

Приложения (братья и сестры)

Наиболее полезным применением здесь для генетической статистики является корреляция между половинами . Напомним, что коэффициент корреляции ( R ) является соотношением ковариации к дисперсии [см. Раздел «связанные атрибуты», например]. Следовательно, r _hs = cov (hs) / s ²_{все HS вместе} = [ ⁠ 1/4 ²_А + ⁠ 1/4 ²_D ] / s ²_P = ⁠ 1/4 ⁠ H ² . ^{[ 61 ]} Корреляция между полной сибами имеет небольшую полезность, будучи r _fs = cov (fs) / s ²_{все fs вместе} = [ ⁠ 1/2 ⁠ s ²_А + ⁠ 1/4 ²_D ] / s ²_П. Предположение о том, что это «приблизительно» ( ⁠ 1/2 ⁠ H ²) это плохой совет.

Конечно, корреляции между братьями и сестрами представляют внутренний интерес в своем собственном праве, совершенно кроме любой утилиты, которую они могут иметь для оценки наследия или генотипических разнообразий.

Может быть, стоит отметить, что [Cov (fs) - Cov (hs)] = ⁠ 1/4 ²_А Эксперименты, состоящие из семейств FS и HS, могут использовать это с использованием внутриклассовой корреляции, чтобы приравнивать компоненты дисперсии эксперимента к этим ковариациям [см. Раздел «Коэффициент взаимосвязи как внутриклассовой корреляции» для обоснования этого].

Предыдущие комментарии, касающиеся эпистаза, снова применяются здесь [см. Раздел «Приложения (Parent-Offspring»].

Выбор

Основные принципы

Генетическое продвижение и давление отбора повторяется

Отбор работает на атрибуте (фенотип), так что люди, которые равны или превышают порог отбора (z _P ), становятся эффективными родителями для следующего поколения. Доля , которую они представляют в базовую популяцию, является давлением отбора . Чем меньше пропорция, тем сильнее давление. Среднее значение выбранной группы (P _S ) превосходит среднее значение базового населения (P ₀ ) по разнице, называемой дифференциалом (S) отбора . Все эти величины фенотипические. «Связывать» с базовыми генами, наследуемость (h ²) используется, выполняя роль коэффициента определения в биометрическом смысле. Ожидаемое генетическое изменение - все еще экспрессируется в фенотипических единицах измерения - называется генетическим продвижением (ΔG) , и получается продуктом дифференциала (ы) отбора и его коэффициентом определения (H ²) Ожидаемое среднее значение потомства (стр. ₁ ) обнаруживается путем добавления генетического продвижения (ΔG) к среднему базовому среднему значению (P ₀ ) . Графики справа показывают, как (начальное) генетическое продвижение больше с более сильным давлением отбора (меньшая вероятность ). Они также показывают, как неуклонно снижается прогресс от последовательных циклов отбора (даже при одном и том же давлении отбора), потому что фенотипическая дисперсия и наследуемость уменьшаются из -за самого отбора. Это обсуждается дальше вскоре.

Таким образом $\Delta G=Sh^{2}$ . ^{[ 14 ]} ^{: 1710–181} и $P_{1}=P_{0}+\Delta G$ . ^{[ 14 ]} ^{: 1710–181}

Узловая наследуемость (ч. ²Обычно используется, тем самым ссылаясь на генскую дисперсию (σ ²_А ) . Однако, если это необходимо, использование наследуемости широкого смысла (h ²) соединится с генотипической дисперсией (σ ²_Г ) ; и даже возможно, аллельная наследуемость [h ²_Eu = (σ ²_как ²_P )] может быть рассмотрено, подключаясь к ( σ ²_а ). [См. Раздел о наследуемости.]

Чтобы применить эти концепции до того, как на самом деле начнется отбор, и, например, предсказание результатов альтернатив (например, выбор порога отбора ), эти фенотипические статистики пересматриваются в отношении свойств нормального распределения, особенно тех, кто касается укора Верхний хвост распределения. В таком рассмотрении стандартизированный дифференциал отбора (i) ″ и стандартизированный используются порог отбора (z) ″ вместо предыдущих «фенотипических» версий. Фенотипический стандартный отклонение (σ _{p (0)} ) также необходим. Это описано в последующем разделе.

Следовательно, Δg = (i σ _p ) h ², где (i σ _{p (0)} ) = s ранее. ^{[ 14 ]} ^{: 1710–181}

Изменения, возникшие в результате повторного выбора

Приведенный выше текст отметил, что последовательный ΔG снижается, потому что «вход» [ фенотипическая дисперсия (σ ²_P ) ] уменьшается на предыдущий выбор. ^{[ 14 ]}^{: 1710–181} Наследственность также уменьшается. Графики слева показывают эти снижения в течение десяти циклов повторного отбора, в течение которых утверждается одно и то же давление выбора. Накопленное генетическое продвижение ( σΔG ) практически достигло своей асимптоты по поколению 6 в этом примере. Это сокращение отчасти зависит от усекающих свойств нормального распределения, а частично от наследуемости вместе с определением мейоза (B ² ) Последние два пункта количественно определяют степень, в которой усечение «смещено» по новым вариациям, возникающим в результате сегрегации и ассортимента во время мейоза. ^{[ 14 ]} ^{: 1710–181}^{[ 27 ]} Это обсуждается в ближайшее время, но здесь обратите внимание на упрощенный результат для недопустимого случайного оплодотворения (F = 0) .

Таким образом: с ²_{P (1)} = σ ²_{P (0)} [1 - I (IZ) ⁠ 1/2 ⁠ H ²] , где i (iz) = k = коэффициент усечения и ⁠ 1/2 ⁠ H ² = R = коэффициент воспроизведения ^{[ 14 ]}^{: 1710–181}^{[ 27 ]} Это можно записать также как σ ²_{P (1)} = σ ²_{P (0)} [1 - KR] , что облегчает более подробный анализ задач отбора.

Здесь я и Z уже были определены, ⁠ 1/2 ⁠ b - мейоза ( определение ²) для f = 0 , а оставшийся символ - это наследуемость. Они обсуждаются далее в следующих разделах. Также обратите внимание, что, в целом, r = b ² час ²Полем Если общее определение мейоза (b ² Используется ) результаты предыдущего инбридинга могут быть включены в выбор. Затем становится фенотипическое уравнение дисперсии:

а ²_{P (1)} = σ ²_{P (0)} [1 - I (IZ) B ² час ²] .

Фенотипическая дисперсия, усеченная выбранной группой ( σ ²_{P (s)} ) просто σ ²_{P (0)} [1 - K] , и его содержащая геновая дисперсия составляет (h ²₀ с ²_{P (S)} ). Предполагая, что отбор не изменил дисперсию окружающей среды , геническая дисперсия для потомства может быть аппроксимирована σ ²_{A (1)} = (σ ²_{P (1)} - σ ²_Е ) . Из этого h ²₁ = (с ²_{A (1)} / σ ²_{P (1)} ) . Подобные оценки могут быть сделаны для σ ²_{G (1)} и h ²₁ , или для σ ²_{A (1)} и H. ²_{ЕС (1),} если требуется.

Альтернатива ΔG

Следующая перестройка полезна для рассмотрения выбора на несколько атрибутов (символов). Это начинается с расширения наследуемости в свои компоненты дисперсии. Δg = i σ _p (σ ²_КАК ²_P ) . Σ σ _p и  ²_P частично отмените, оставив соло σ _p . Далее, σ ²_Внутри наследуемость может быть расширена как ( σ _a × σ _a ), что приводит к:

Дифференциал отбора и нормальное распределение

Δg = i σ _a (σ _a / σ _p ) = i σ _a h .

Соответствующие повторные аренки могут быть сделаны с использованием альтернативной наследия, давая ΔG = I σ _g h или Δg = i σ _a h _eu .

Модели полигенной адаптации в генетике популяции

Этот традиционный взгляд на адаптацию в количественной генетике обеспечивает модель для того, как выбранный фенотип изменяется с течением времени, в зависимости от дифференциала и наследуемости отбора. Однако он не дает понимания (и не зависит от) ни одной из генетических деталей - в частности, количества участвующих локусов, частот их аллелей и размеров эффекта, а также изменения частоты, обусловленные отбором. Это, напротив, находится в центре внимания к полигенной адаптации ^{[ 62 ]} В области генетики популяции . Недавние исследования показали, что такие черты, как рост, развивались у людей в течение последних нескольких тысяч лет в результате сдвигов малых аллелей в тысячах вариантов, которые влияют на высоту. ^{[ 63 ]}^{[ 64 ]}^{[ 65 ]}

Фон

Стандартизированный выбор - нормальное распределение

Вся базовая популяция изложена нормальной кривой ^{[ 59 ]}^: 78–89 Направо. Вдоль оси Z есть каждое значение атрибута от наименьшего до наибольшего, а высота от этой оси до самой кривой - частота значения на оси ниже. Уравнение для поиска этих частот для «нормальной» кривой (кривая «общего опыта») дается в эллипсе. Обратите внимание, что он включает среднее ( μ ) и дисперсию ( σ ²) Двигаясь бесконечно вдоль оси Z, частоты соседних значений могут быть «сложены» рядом с предыдущим, тем самым накапливая область, которая представляет вероятность получения всех значений в стеке. [Это интеграция из исчисления.] Выбор фокусируется на такой области вероятности, будучи заштрихованным от порога отбора (z) до конца верхнего хвоста кривой. Это давление отбора . Выбранная группа (эффективные родители следующего поколения) включают все значения фенотипа от z до «конца» хвоста. ^{[ 66 ]} Среднее значение выбранной группы составляет μ _S , а разница между ней и средним базовым средним ( μ ) представляет дифференциал (ы) отбора . Принимая частичную интеграцию по сравнению с интересующими кривыми и некоторой перегруппировкой алгебры, можно показать, что «дифференциал отбора» составляет s = [y (σ / prob.)] , Где y - частота значения при «Порог отбора» ( ордината Z ) Z . ^{[ 13 ]}^{: 226–230} Перестановление этой связи дает S / σ = y / sper. , левая сторона которой, на самом деле, дифференциал отбора, деленная на стандартное отклонение -то есть стандартизированный дифференциал отбора (i) . Правая сторона отношений обеспечивает «оценку» для I -ординаты порога отбора, разделенного на давление отбора . Таблицы нормального распределения ^{[ 49 ]} ^{: 547–548} Можно использовать, но таблицы самого I также доступны. ^{[ 67 ]}^{: 123–124} Последняя ссылка также дает значения I , скорректированные для небольших популяций (400 и меньше), ^{[ 67 ]}^{: 111–122} где «квази-инфинтность» нельзя предположить (но предполагалось в контур «нормальное распределение» выше). Стандартизированный дифференциал отбора ( i ) также известен как интенсивность отбора . ^{[ 14 ]}^{: 174, 186}

Наконец, поперечная связь с различной терминологией в предыдущем подразделе может быть полезно: μ (здесь) = "p ₀ " (там), μ _s = "p _s " и σ ² = "σ ²_P ".

Определение мейоза - анализ репродуктивного пути

Репродуктивные коэффициенты определения и инбридинга

Определение мейоза (б ²) является коэффициентом определения мейоза, который является дивизией клеток, при котором родители генерируют гаметы. Следуя принципам стандартизированной частичной регрессии , из которых анализ путей является фактической ориентированной версией, Sewall Wright проанализировал пути потока генов во время сексуального размножения и установил «сильные стороны вклада» ( коэффициенты определения ) различных компонентов в общий результат. ^{[ 27 ]}^{[ 37 ]} Анализ пути включает в себя частичные корреляции , а также коэффициенты частичной регрессии (последние являются коэффициентами пути ). Линии с одной головкой стрелки являются направленными определяющими путями , а линии с двойными стрелками являются корреляционными соединениями . Отслеживание различных маршрутов в соответствии с правилами анализа пути эмулирует алгебру стандартизированной частичной регрессии. ^{[ 55 ]}

Диаграмма пути слева представляет этот анализ сексуального размножения. Из его интересных элементов важным в контексте отбора является мейоз . Вот где происходит сегрегация и ассортимент - процессы, которые частично улучшают усечение фенотипической дисперсии, которая возникает в результате отбора. Коэффициенты пути B - это пути мейоза. Эти помеченные A являются путями оплодотворения. Корреляция между гаметами от одного и того же родителя ( G ) является мейотической корреляцией . Что между родителями в том же поколении равен r _a . Это между гаметами от разных родителей ( F ) стало известно впоследствии как коэффициент инбридинга . ^{[ 13 ]}^: 64 Простые числа (') указывают на поколение (T-1) , а ООН -заправочная указывает на поколение t . Здесь даны некоторые важные результаты настоящего анализа. Сьюалл Райт интерпретировал много с точки зрения коэффициентов инбридинга. ^{[ 27 ]}^{[ 37 ]}

Определение мейоза ( б ²) является ⁠ 1/2 ⁠ и ( 1+г) равны ⁠ 1/2 G (T - ⁠ (1 + F _(T-1) ) , подразумевая, что = F ₁₎ . ^{[ 68 ]} С неразличием случайного оплодотворения, f _(t-1) ) = 0, давая b ² = ⁠ 1/2 . , как используется ⁠ в разделе «Выбор» выше Однако, осознавая его фон, другие модели оплодотворения могут использоваться по мере необходимости. Другое определение также включает в себя инбридинги - определение оплодотворения ( ²) равняется 1 / [2 (1 + f _t )] . Также другой корреляцией является индикатор инбридинга- r _a = 2 f _t / (1 + f _(t-1) ) , также известный как коэффициент взаимосвязи . [Не путайте это с коэффициентом родства -альтернативным названием коэффициента коэффициента . См. Введение в раздел «Отношения».] Это в _{повторяется} подразделе по дисперсии и выбору.

Эти связи с инбридингом показывают интересные аспекты о сексуальном размножении, которые не сразу очевидны. Графики на правильный график коэффициенты мейоза и сингамии (оплодотворения) определения против коэффициента инбридинга. Там выясняется, что по мере увеличения инбридинга мейоз становится более важным (коэффициент увеличивается), в то время как сингамия становится менее важной. Общая роль размножения [продукт двух предыдущих коэффициентов - r ²] остается прежним. ^{[ 69 ]} Это увеличение B ² особенно актуально для отбора, потому что это означает, что усечение отбора фенотипической дисперсии компенсируется в меньшей степени во время последовательности отборов при сопровождении инбридинга (что часто бывает).

Генетический дрейф и выбор

Предыдущие разделы рассматривали дисперсию как «помощник» для отбора , и стало очевидно, что они хорошо работают вместе. В количественной генетике отбор обычно рассматривается в этом «биометрическом» моде, но изменения в средствах (как контролируемые с помощью ΔG) отражают изменения в частотах аллеля и генотипа под этой поверхностью. Справление в раздел по «генетическому дрейфу» напоминает, что это также влияет на изменения в частотах аллеля и генотипа, а также связанные с ними средства; и что это сопутствующий аспект для рассеивания, рассматриваемой здесь («Другая сторона той же монеты»). Тем не менее, эти две силы частоты изменяются редко согласованно и могут часто действовать противостоять друг другу. Один (выбор) является «направленным», обусловленным давлением отбора, действующим на фенотип: другой (генетический дрейф) обусловлен «шансом» при оплодотворениях (биномиальные вероятности образцов гамета). Если эти два склонны к одной и той же частоте аллелей, их «совпадение» является вероятностью получения этой частоты образца в генетическом дрифте: вероятность того, что они «в конфликте», однако, является Сумма вероятностей всех альтернативных частот образцов . В крайних случаях единая сингамия может отменить то, чего достигли, и доступны вероятности его происходящих. Важно помнить об этом. Тем не менее, генетический дрейф, приводящий к частотам выборки, сходных с частотой цели выбора, не приводит к столь радикальному исходу - приводит к замедлению прогресса в достижении целей отбора.

Коррелированные атрибуты

При совместном наблюдении за двумя (или более) атрибутами ( например, высотой и массой) можно заметить, что они варьируются вместе по мере изменения генов или среды. Это совместное использование измеряется ковариацией , которая может быть представлена « COV » или θ . ^{[ 43 ]} Это будет положительно, если они меняются друг с другом в одном направлении; или отрицательно, если они меняются друг с другом, но в противоположном направлении. Если два атрибута различаются независимо друг от друга, ковариация будет нулевой. Степень связи между атрибутами определяется количественно по коэффициенту корреляции (символ R или ρ ). В общем, коэффициент корреляции является соотношением ковариации к геометрическому среднему значению ^{[ 70 ]} из двух вариантов атрибутов. ^{[ 59 ]} ^{: 196–198} Наблюдения обычно встречаются в фенотипе, но в исследованиях они также могут происходить в «эффективном гаплотипе» (эффективный генный продукт) [см. Рисунок справа]. Следовательно, ковариация и корреляция могут быть «фенотипическими» или «молекулярными» или любым другим обозначением, которое позволяет модель анализа. Фенотипическая ковариация является «самым внешним» слоем и соответствует «обычной» ковариации в биометрии/статистике. Тем не менее, он может быть разделен по любой соответствующей модели исследования так же, как и фенотипическая дисперсия. Для каждого разделения ковариации существует соответствующий раздел корреляции. Некоторые из этих разделов приведены ниже. Первый индекс (G, A и т. Д.) Указывает раздел. Подписки второго уровня (x, y) являются «хранителями» для любых двух атрибутов.

Первым примером является фенотип без участия .

{r_{P_{XY}}}={{cov_{P_{XY}}} \over {\sqrt {\sigma _{P_{X}}^{2}\sigma _{P_{Y}}^{2}}}}

Генетические разделы (а) «генотипический» (общий генотип), (б) «генические» (ожидания замены) и (c) «аллель» (гомозигота).

(а) ${r_{G_{XY}}}={{cov_{G_{XY}}} \over {\sqrt {\sigma _{G_{X}}^{2}\sigma _{G_{Y}}^{2}}}}$

(б) ${r_{A_{XY}}}={{cov_{A_{XY}}} \over {\sqrt {\sigma _{A_{X}}^{2}\sigma _{A_{Y}}^{2}}}}$

(c) ${r_{a_{XY}}}={{cov_{a_{XY}}} \over {\sqrt {\sigma _{a_{X}}^{2}\sigma _{a_{Y}}^{2}}}}$

С соответствующим спроектированным экспериментом негенетическое также можно получить разделение (окружающая среда).

{r_{E_{XY}}}={{cov_{E_{XY}}} \over {\sqrt {\sigma _{E_{X}}^{2}\sigma _{E_{Y}}^{2}}}}

Основные причины корреляции

Есть несколько разных способов, которыми может возникнуть фенотипическая корреляция. Дизайн исследования, размер выборки, статистика выборки и другие факторы могут влиять на способность различать их с более или менее статистической уверенностью. Каждый из них имеет различное научное значение и имеет отношение к различным областям работы.

Прямая причинность

Один фенотип может непосредственно влиять на другой фенотип, влияя на развитие, метаболизм или поведение.

Генетические пути

Общий ген или транскрипционный фактор в биологических путях для двух фенотипов может привести к корреляции.

Метаболические пути

Метаболические пути от гена к фенотипу являются сложными и разнообразными, но в них лежат причины корреляции среди атрибутов.

Факторы развития и окружающей среды

Многочисленные фенотипы могут зависеть от одних и тех же факторов. Например, существует множество фенотипических атрибутов, коррелирующих с возрастом, и, таким образом, высота, вес, потребление калорий, эндокринная функция и все больше, все имеют корреляцию. Исследование в поисках других общих факторов должно исключить их в первую очередь.

Коррелированные генотипы и селективное давление

Различия между подгруппами в популяции, между популяциями или селективными смещениями могут означать, что некоторые комбинации генов перепредставлены по сравнению с тем, что можно ожидать. Хотя гены могут не оказывать существенного влияния друг на друга, между ними все еще может существовать корреляция, особенно когда определенные генотипы не позволяют смешивать. Популяции в процессе генетической дивергенции или уже подвергаясь, чтобы иметь разные характерные фенотипы, ^{[ 71 ]} Это означает, что при рассмотрении вместе появляется корреляция. Фенотипические качества у людей, которые в основном зависят от происхождения, также вызывают корреляции этого типа. Это также можно наблюдать у породы собак, где несколько физических особенностей составляют отчетливость данной породы и поэтому коррелируют. ^{[ 72 ]} Асортативное спаривание , которое является сексуально селективным давлением для спаривания с аналогичным фенотипом, может привести к тому, что генотипы остаются более чем, чем можно было бы ожидать. ^{[ 73 ]}

Смотрите также

Сноски и ссылки

^ Андерберг, Майкл Р. (1973). Кластерный анализ для приложений . Нью -Йорк: Академическая пресса.
^ Мендель, Грегор (1866). «Попытки над гибридом растений». Переговоры о естественных исследовательских ассоциации в Брно . IV
^ Jump up to: ^а ^{беременный} ^в Мендель, Грегор (1891). «Эксперименты по гибридизации растений». Дж. Рой. Горь Соц (Лондон) . XXV . Перевод Бейтсона, Уильям: 54–78.
^ Мендель Г.; Бейтсон В. (1891) Документ с дополнительными комментариями Бейтсона перепечатана в: Sinnott EW; Dunn Lc; Добжанский Т. (1958). «Принципы генетики»; Нью-Йорк, МакГроу-Хилл: 419-443. Сноска 3, стр. 422 идентифицирует Бейтсона в качестве исходного переводчика и предоставляет ссылку на этот перевод.
^ QTL - это область в геноме ДНК, которая влияет или связан с количественными фенотипическими признаками.
^ Уотсон, Джеймс Д.; Гилман, Майкл; Витковски, Ян; Zoller, Mark (1998). Рекомбинантная ДНК (вторая (7 -я печать) изд.). Нью -Йорк: WH Freeman (Scientific American Books). ISBN 978-0-7167-1994-6 .
^ Jain, HK; Kharkwal, MC, eds. (2004). Разведение растений - Менделянскую до молекулярных подходов . Бостон Дордехт Лондон: Клуверские академические издатели. ISBN 978-1-4020-1981-4 .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Фишер, Р.А. (1918). «Корреляция между родственниками в отношении предположения Менделевского наследования» . Сделки Королевского общества Эдинбурга . 52 (2): 399–433. doi : 10.1017/s0080456800012163 . S2CID 181213898 . Архивировано из оригинала 8 октября 2020 года . Получено 7 сентября 2020 года .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин Сталь, RGD; Торри, Дж. Х. (1980). Принципы и процедуры статистики (2 изд.). Нью-Йорк: МакГроу-Хилл. ISBN 0-07-060926-8 .
^ Иногда используются другие символы, но они распространены.
^ Эффект аллеля-это среднее фенотипическое отклонение гомозиготы от средней точки двух контрастных гомозиготных фенотипов в одном локусе, когда наблюдается по бесконечности всех фоновых генотипов и сред. На практике оценки из больших непредвзятых образцов заменяют параметр.
^ Эффект доминирования-это среднее фенотипическое отклонение гетерозиготы от средней точки двух гомозигот в одном локусе, когда наблюдается по бесконечности всех фоновых генотипов и сред. На практике оценки из больших непредвзятых образцов заменяют параметр.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж ^k ^л ^м ^не ^а ^п ^Q. ^{ведущий} ^с ^Т ^в ^v ^В ^х ^и ^С ^аа ^Аб ^и ^{объявление} ^Но ^из ^в ^{нравиться} Кроу, JF; Кимура, М. (1970). Введение в теорию генетики популяции . Нью -Йорк: Харпер и Роу.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж ^k ^л ^м ^не ^а ^п ^Q. ^{ведущий} ^с ^Т ^в ^v ^В ^х ^и ^С ^аа ^Аб ^и ^{объявление} ^Но ^из ^в ^{нравиться} ^это ^к ^и ^ал
Falconer, DS; Mackay, Trudy FC (1996). Введение в количественную генетику (четвертое изд.). Харлоу: Лонгман. ISBN 978-0582-24302-6 .
- Уильям Г. Хилл; Trudy FC Mackay (август 2004 г.). «DS Falconer и введение в количественную генетику» . Генетика . 167 (4): 1529–1536. doi : 10.1093/Genetics/167.4.1529 . PMC 1471025 . PMID 15342495 .
^ Мендель прокомментировал эту конкретную тенденцию к F1> P1, т. Е. Свидетельство гибридной энергии по длине стебля. Однако разница может быть не значительной. (Взаимосвязь между диапазоном и стандартным отклонениями известна [Steel and Torrie (1980): 576], что позволяет провести тест приблизительной значимости для настоящего нынешнего различия.)
^ Ричардс, AJ (1986). Системы селекции растений . Бостон: Джордж Аллен и Unwin. ISBN 0-04-581020-6 .
^ Джейн Гудолл Институт. «Социальная структура шимпанзе» . Шимпанзе Центральный . Архивировано из оригинала 3 июля 2008 года . Получено 20 августа 2014 года .
^ Гордон, Ян Л. (2000). «Количественная генетика аллогамного F2: происхождение случайно оплодотворенных популяций» . Наследственность . 85 : 43–52. doi : 10.1046/j.1365-2540.2000.00716.x . PMID 10971690 .
^ F2, полученный в результате самочувствительных индивидуумов F1 ( аутогамный F2), однако, не является происхождением случайно оплодотворенной структуры популяции. См. Гордон (2001).
^ Замок, мы (1903). «Закон наследственности Гальтона и Менделя и некоторые законы, регулирующие улучшение рас в результате отбора». Труды Американской академии искусств и наук . 39 (8): 233–242. doi : 10.2307/20021870 . HDL : 2027/Hvd.32044106445109 . JSTOR 20021870 .
^ Харди, GH (1908). «Мендельские пропорции в смешанной популяции» . Наука . 28 (706): 49–50. Bibcode : 1908sci .... 28 ... 49H . doi : 10.1126/science.28.706.49 . PMC 2582692 . PMID 17779291 .
^ Вайнберг, У. (1908). «О выявлении возрождения у людей». Ежегодный. Ассоциация Ф. Ватерл. Naturk, Württem . 64 : 368–382.
^ Обычно в научной этике открытие названо в честь самого раннего человека, чтобы предложить его. Замок, однако, кажется, был упущен из виду: и позже, когда он был заново, название «Харди Вайнберг» был настолько вездесущим, что казалось, что это было слишком поздно, чтобы обновить его. Возможно, равновесие "Castle Hardy Weinberg" было бы хорошим компромиссом?
^ Jump up to: ^а ^{беременный} Гордон, Ян Л. (1999). «Количественная генетика гибридов внутривидовых» . Наследственность . 83 (6): 757–764. doi : 10.1046/j.1365-2540.1999.00634.x . PMID 10651921 .
^ Гордон, Ян Л. (2001). «Количественная генетика аутогамного F2» . Hereditas . 134 (3): 255–262. doi : 10.1111/j.1601-5223.2001.00255.x . PMID 11833289 .
^ Райт С. (1917). «Средняя корреляция в подгруппах населения». J. Wash. Acad. Наука 7 : 532–535.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин Райт С. (1921). «Системы спаривания. I. Биометрические отношения между родителем и потомством» . Генетика . 6 (2): 111–123. doi : 10.1093/Genetics/6.2.111 . PMC 1200501 . PMID 17245958 .
^ Sinnott, Edmund W.; Данн, LC; Добжанский, Теодосий (1958). Принципы генетики . Нью-Йорк: МакГроу-Хилл.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и Фишер, Р.А. (1999). Генетическая теория естественного отбора (Variorum ed.). Оксфорд: издательство Оксфордского университета. ISBN 0-19-850440-3 .
^ Jump up to: ^а ^{беременный} Кокран, Уильям Г. (1977). Методы отбора проб (третье изд.). Нью -Йорк: Джон Уайли и сыновья.
^ Это впоследствии изложено в разделе генотипических дисперсий.
^ Оба используются обычно.
^ См. Предыдущие цитаты.
^ Аллард, RW (1960). Принципы размножения растений . Нью -Йорк: Джон Уайли и сыновья.
^ Jump up to: ^а ^{беременный} Это читается как "σ ²_P и/или σ ²_Q ". Как P и Q дополняют, σ ²_P ≡ ≡ ²_Q и σ ²_P = σ ²_Q.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я Гордон, Иллинойс (2003). «Уточнения к разделению инбредной генотипической дисперсии» . Наследственность . 91 (1): 85–89. doi : 10.1038/sj.hdy.6800284 . PMID 12815457 .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж Райт, Сьюолл (1951). «Генетическая структура популяций». Анналы евгеники . 15 (4): 323–354. doi : 10.1111/j.1469-1809.1949.tb02451.x . PMID 24540312 .
^ Помните, что проблема Auto/Allo -Bygosity может возникнуть только для гомологичных аллелей (то есть A и A , или A и A ), а не для не -гомологичных аллелей ( A и A ), которые не могут иметь одинаковый аллель. источник .
^ Обычно использовать «α», а не «β» для этой величины (например, в уже упоминавшихся ссылках). Последнее используется здесь, чтобы минимизировать любую путаницу с «А», которая часто встречается также в этих же уравнениях.
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Мазер, Кеннет; Джинкс, Джон Л. (1971). Биометрическая генетика . Тол. 26 (2 изд.). Лондон: Чепмен и Холл. С. 349–364. doi : 10.1038/hdy.1971.47 . ISBN 0-412-10220-x Полем PMID 5285746 . S2CID 46065232 . {{cite book}}: |journal= игнорируется ( помощь )
^ В терминологии Мазер фракция перед буквой является частью ярлыка для компонента.
^ В каждой строке этих уравнений компоненты представлены в одном и том же порядке. Следовательно, вертикальное сравнение компонентом дает определение каждого в различных формах. Таким образом, компоненты Mather были переведены в рыболовные символы: таким образом, облегчая их сравнение. Перевод также был получен формально. См. Гордон 2003.
^ Jump up to: ^а ^{беременный} Ковариация-это совместная вещество между двумя наборами данных. Подобно дисперсии, он основан на сумме перекрестных продуктов (SCP) вместо SS. Исходя из этого, ясно, что дисперсия - это всего лишь особая форма ковариации.
^ Хейман, Би (1960). «Теория и анализ Креста Диалеля. III» . Генетика . 45 (2): 155–172. doi : 10.1093/Genetics/45.2.155 . PMC 1210041 . PMID 17247915 .
^ Было отмечено, что когда p = q или когда d = 0 , β [= a+(qp) d] «уменьшается» до a . В таких обстоятельствах σ ²_A = σ ²_а - но только численно . Они все еще не стали единственной и той же идентичностью. Это было бы аналогичным Sequitur с тем, что было отмечено ранее для «отклонений замены», рассматриваемых как «доминирование» для генной модели.
^ Вспомогательные цитаты уже даны в предыдущих разделах.
^ Фишер отметил, что эти остатки возникли благодаря воздействию доминирования: но он воздерживался от их определения как «дисперсии доминирования». (См. Вышеизложенные цитаты.) Обратитесь к более ранним обсуждениям в настоящем документе.
^ При рассмотрении происхождения терминов: Фишер также предложил слово «дисперсию» для этой меры изменчивости. См. Фишер (1999), с.311 и Фишер (1918).
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Snedecor, George W.; Кокран, Уильям Г. (1967). Статистические методы (шестой изд.). Эймс: издательство штата Айова Университет. ISBN 0-8138-1560-6 .
^ Jump up to: ^а ^{беременный} ^в Кендалл, мг; Стюарт, А. (1958). Усовершенствованная теория статистики. Том 1 (2 -е изд.). Лондон: Чарльз Гриффин.
^ Обычная практика не иметь подписки на экспериментальную дисперсию «ошибки».
^ В биометрии это дисперсионное рационирование, в котором часть выражается как фракция целого: то есть коэффициент определения . Такие коэффициенты используются особенно в регрессионном анализе . Стандартизированной версией регрессионного анализа является анализ пути . Здесь стандартизация означает, что данные были впервые разделены на их собственные экспериментальные стандартные ошибки для объединения шкал для всех атрибутов. Это генетическое использование является еще одним важным появлением коэффициентов определения.
^ Гордон, Иллинойс; Byth, de; Balaam, LN (1972). «Разница коэффициентов наследуемости, оцененные по компонентам фенотипической дисперсии». Биометрия . 28 (2): 401–415. doi : 10.2307/2556156 . JSTOR 2556156 . PMID 5037862 .
^ Дом, М.Р. (2002). «Оценки повторяемости не всегда устанавливают верхний предел на наследуемость» . Функциональная экология . 16 (2): 273–280. Bibcode : 2002fueco..16..273m . doi : 10.1046/j.1365-2435.2002.00621.x .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Ли, Чинг Чун (1977). Анализ пути - праймер (вторая печать с исправлениями изд.). Pacific Grove: Boxwood Press. ISBN 0-910286-40-x .
^ квадратный корн их продукта
^ Moroney, MJ (1956). Факты из цифр (третье изд.). Harmondsworth: книги пингвинов.
^ Jump up to: ^а ^{беременный} Дрейпер, Норман Р.; Смит, Гарри (1981). Применяемый регрессионный анализ (второе изд.). Нью -Йорк: Джон Уайли и сыновья. ISBN 0-471-02995-5 .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Balaam, LN (1972). Основы биометрии . Лондон: Джордж Аллен и Unwin. ISBN 0-04-519008-9 .
^ В прошлом обе формы ковариации родителей-скрещивания были применены к этой задаче оценки h ², но, как отмечалось в подразделе выше, только один из них ( COV (MPO) ) на самом деле уместен. Однако COV (PO) полезен для оценки H ² Как видно в основном тексте следующего.
^ Обратите внимание, что тексты, которые игнорируют компонент доминирования COV (HS) ошибочно предполагают, что r _hs «приблизительно» ( ⁠ 1/4 ⁠ H ² ).
^ Причард, Джонатан К.; Пикрелл, Джозеф К.; Куп, Грэм (23 февраля 2010 г.). «Генетика адаптации человека: жесткие зачистки, мягкие зачистки и полигенная адаптация» . Текущая биология . 20 (4): R208–215. Bibcode : 2010cbio ... 20.r208p . doi : 10.1016/j.cub.2009.11.055 . ISSN 1879-0445 . PMC 2994553 . PMID 20178769 .
^ Турчин, Майкл С.; Чиан, Чарльстон, WK; Палмер, Кэмерон Д.; Sankararaman, Sriram; Рейх, Дэвид; Генетическое исследование консорциума антропометрических признаков (гигантских); Хиршхорн, Джоэл Н. (сентябрь 2012 г.). «Свидетельство широко распространенного отбора о изменении в Европе в SNP, связанных с высотой» . Природа генетика . 44 (9): 1015–1019. doi : 10.1038/ng.2368 . ISSN 1546-1718 . PMC 3480734 . PMID 22902787 .
^ Берг, Джереми Дж.; Куп, Грэм (август 2014 г.). «Генетический сигнал популяции полигенной адаптации» . PLOS Genetics . 10 (8): E1004412. doi : 10.1371/journal.pgen.1004412 . ISSN 1553-7404 . PMC 4125079 . PMID 25102153 .
^ Поле, яир; Бойл, Эван А.; Телис, Натали; Гао, Ziyue; Голтон, Кайл Дж.; Голан, Дэвид; Yengo, Loic; Рошело, Гислан; Froguel, Филипп (11 ноября 2016 г.). «Обнаружение адаптации человека в течение последних 2000 лет» . Наука . 354 (6313): 760–764. Bibcode : 2016sci ... 354..760f . doi : 10.1126/science.AAG0776 . ISSN 0036-8075 . PMC 5182071 . PMID 27738015 .
^ Теоретически, хвост бесконечен , но на практике есть квази-энд .
^ Jump up to: ^а ^{беременный} Беккер, Уолтер А. (1967). Руководство по процедурам в количественной генетике (второе изд.). Пулман: Вашингтонский государственный университет.
^ Обратите внимание, что это б ² является коэффициентом происхождения ( F _AA ) переписанного анализа родословного, с «уровнем генерации» вместо «A» внутри скобков.
^ Есть небольшое «колебание», возникающее из -за того, что б ² изменяет одно поколение позади ²- Экспонируйте их уравнения инбридинга.
^ Оценивается как квадратный корн их продукта.
^ «Репродуктивная изоляция» . Понимание эволюции . Беркли. 16 апреля 2021 года.
^ Serres-Armero, A; Дэвис, BW; Поволоцкая, есть; Morcillo-Suarez, C; Plassais, J; Хуан, D; Остранд, EA; Marques-Bonet, t (май 2021 г.). «Изменение числа копий лежит в основе сложных фенотипов у домашних пород собак и других Canids» . Исследование генома . 31 (5): 762–774. doi : 10.1101/gr.266049.120 . PMC 8092016 . PMID 33863806 .
^ Цзян, Юэксин; Болник, Даниэль I.; Киркпатрик, Марк (2013). «Ассортативное спаривание у животных» (PDF) . Американский натуралист . 181 (6): E125 - E138. doi : 10.1086/670160 . HDL : 2152/31270 . PMID 23669548 . S2CID 14484725 .

Дальнейшее чтение

Falconer DS & Mackay TFC (1996). Введение в количественную генетику, 4 -е издание. Лонгман, Эссекс, Англия.
Caballero, A (2020) Количественная генетика. Издательство Кембриджского университета.
Lynch M & Walsh B (1998). Генетика и анализ количественных признаков. Синауэр, Сандерленд, Массачусетс.
Рофф Д.А. (1997). Эволюционная количественная генетика. Чепмен и Холл, Нью -Йорк.
Сейкора, Тони. Наука о животных 3221 Разведение животных. Технический Миннеаполис: Университет Миннесоты, 2011. Печать.

Внешние ссылки

Уравнение заводчика
Количественные генетические ресурсы Майкла Линча и Брюса Уолша , включая два объема их учебника, генетики и анализа количественных признаков и эволюции и отбора количественных признаков .
Ресурсы Ника Бартона и соавт. Полем Из учебника, эволюция .
G-матрица онлайн

[Anderberg_1973-1] Андерберг, Майкл Р. (1973). Кластерный анализ для приложений . Нью -Йорк: Академическая пресса.

[Mendel-2] Мендель, Грегор (1866). «Попытки над гибридом растений». Переговоры о естественных исследовательских ассоциации в Брно . IV

[Mendel_Bateson-3] Jump up to: ^а ^{беременный} ^в Мендель, Грегор (1891). «Эксперименты по гибридизации растений». Дж. Рой. Горь Соц (Лондон) . XXV . Перевод Бейтсона, Уильям: 54–78.

[4] Мендель Г.; Бейтсон В. (1891) Документ с дополнительными комментариями Бейтсона перепечатана в: Sinnott EW; Dunn Lc; Добжанский Т. (1958). «Принципы генетики»; Нью-Йорк, МакГроу-Хилл: 419-443. Сноска 3, стр. 422 идентифицирует Бейтсона в качестве исходного переводчика и предоставляет ссылку на этот перевод.

[5] QTL - это область в геноме ДНК, которая влияет или связан с количественными фенотипическими признаками.

[W&G&W&Z_1998-6] Уотсон, Джеймс Д.; Гилман, Майкл; Витковски, Ян; Zoller, Mark (1998). Рекомбинантная ДНК (вторая (7 -я печать) изд.). Нью -Йорк: WH Freeman (Scientific American Books). ISBN 978-0-7167-1994-6 .

[J&K_2004-7] Jain, HK; Kharkwal, MC, eds. (2004). Разведение растений - Менделянскую до молекулярных подходов . Бостон Дордехт Лондон: Клуверские академические издатели. ISBN 978-1-4020-1981-4 .

[Fisher_1918-8] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Фишер, Р.А. (1918). «Корреляция между родственниками в отношении предположения Менделевского наследования» . Сделки Королевского общества Эдинбурга . 52 (2): 399–433. doi : 10.1017/s0080456800012163 . S2CID 181213898 . Архивировано из оригинала 8 октября 2020 года . Получено 7 сентября 2020 года .

[S_&_T-9] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин Сталь, RGD; Торри, Дж. Х. (1980). Принципы и процедуры статистики (2 изд.). Нью-Йорк: МакГроу-Хилл. ISBN 0-07-060926-8 .

[10] Иногда используются другие символы, но они распространены.

[11] Эффект аллеля-это среднее фенотипическое отклонение гомозиготы от средней точки двух контрастных гомозиготных фенотипов в одном локусе, когда наблюдается по бесконечности всех фоновых генотипов и сред. На практике оценки из больших непредвзятых образцов заменяют параметр.

[12] Эффект доминирования-это среднее фенотипическое отклонение гетерозиготы от средней точки двух гомозигот в одном локусе, когда наблюдается по бесконечности всех фоновых генотипов и сред. На практике оценки из больших непредвзятых образцов заменяют параметр.

[Crow_&_Kimura-13] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж ^k ^л ^м ^не ^а ^п ^Q. ^{ведущий} ^с ^Т ^в ^v ^В ^х ^и ^С ^аа ^Аб ^и ^{объявление} ^Но ^из ^в ^{нравиться} Кроу, JF; Кимура, М. (1970). Введение в теорию генетики популяции . Нью -Йорк: Харпер и Роу.

[Falconer_1996-14] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж ^k ^л ^м ^не ^а ^п ^Q. ^{ведущий} ^с ^Т ^в ^v ^В ^х ^и ^С ^аа ^Аб ^и ^{объявление} ^Но ^из ^в ^{нравиться} ^это ^к ^и ^ал Falconer, DS; Mackay, Trudy FC (1996). Введение в количественную генетику (четвертое изд.). Харлоу: Лонгман. ISBN 978-0582-24302-6 .
Уильям Г. Хилл; Trudy FC Mackay (август 2004 г.). «DS Falconer и введение в количественную генетику» . Генетика . 167 (4): 1529–1536. doi : 10.1093/Genetics/167.4.1529 . PMC 1471025 . PMID 15342495 .

[15] Уильям Г. Хилл; Trudy FC Mackay (август 2004 г.). «DS Falconer и введение в количественную генетику» . Генетика . 167 (4): 1529–1536. doi : 10.1093/Genetics/167.4.1529 . PMC 1471025 . PMID 15342495 .

[15] Мендель прокомментировал эту конкретную тенденцию к F1> P1, т. Е. Свидетельство гибридной энергии по длине стебля. Однако разница может быть не значительной. (Взаимосвязь между диапазоном и стандартным отклонениями известна [Steel and Torrie (1980): 576], что позволяет провести тест приблизительной значимости для настоящего нынешнего различия.)

[Richards_1986-16] Ричардс, AJ (1986). Системы селекции растений . Бостон: Джордж Аллен и Unwin. ISBN 0-04-581020-6 .

[Chimpanzees_2014-17] Джейн Гудолл Институт. «Социальная структура шимпанзе» . Шимпанзе Центральный . Архивировано из оригинала 3 июля 2008 года . Получено 20 августа 2014 года .

[Gordon_2000-18] Гордон, Ян Л. (2000). «Количественная генетика аллогамного F2: происхождение случайно оплодотворенных популяций» . Наследственность . 85 : 43–52. doi : 10.1046/j.1365-2540.2000.00716.x . PMID 10971690 .

[19] F2, полученный в результате самочувствительных индивидуумов F1 ( аутогамный F2), однако, не является происхождением случайно оплодотворенной структуры популяции. См. Гордон (2001).

[Castle_1903-20] Замок, мы (1903). «Закон наследственности Гальтона и Менделя и некоторые законы, регулирующие улучшение рас в результате отбора». Труды Американской академии искусств и наук . 39 (8): 233–242. doi : 10.2307/20021870 . HDL : 2027/Hvd.32044106445109 . JSTOR 20021870 .

[Hardy_1908-21] Харди, GH (1908). «Мендельские пропорции в смешанной популяции» . Наука . 28 (706): 49–50. Bibcode : 1908sci .... 28 ... 49H . doi : 10.1126/science.28.706.49 . PMC 2582692 . PMID 17779291 .

[Weinberg_1908-22] Вайнберг, У. (1908). «О выявлении возрождения у людей». Ежегодный. Ассоциация Ф. Ватерл. Naturk, Württem . 64 : 368–382.

[23] Обычно в научной этике открытие названо в честь самого раннего человека, чтобы предложить его. Замок, однако, кажется, был упущен из виду: и позже, когда он был заново, название «Харди Вайнберг» был настолько вездесущим, что казалось, что это было слишком поздно, чтобы обновить его. Возможно, равновесие "Castle Hardy Weinberg" было бы хорошим компромиссом?

[Gordon_1999-24] Jump up to: ^а ^{беременный} Гордон, Ян Л. (1999). «Количественная генетика гибридов внутривидовых» . Наследственность . 83 (6): 757–764. doi : 10.1046/j.1365-2540.1999.00634.x . PMID 10651921 .

[Gordon_2001-25] Гордон, Ян Л. (2001). «Количественная генетика аутогамного F2» . Hereditas . 134 (3): 255–262. doi : 10.1111/j.1601-5223.2001.00255.x . PMID 11833289 .

[Wright_1917-26] Райт С. (1917). «Средняя корреляция в подгруппах населения». J. Wash. Acad. Наука 7 : 532–535.

[Wright_1921_a-27] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин Райт С. (1921). «Системы спаривания. I. Биометрические отношения между родителем и потомством» . Генетика . 6 (2): 111–123. doi : 10.1093/Genetics/6.2.111 . PMC 1200501 . PMID 17245958 .

[Sinnott_Dunn_&_Dobzhansky-28] Sinnott, Edmund W.; Данн, LC; Добжанский, Теодосий (1958). Принципы генетики . Нью-Йорк: МакГроу-Хилл.

[Fisher_1999-29] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и Фишер, Р.А. (1999). Генетическая теория естественного отбора (Variorum ed.). Оксфорд: издательство Оксфордского университета. ISBN 0-19-850440-3 .

[Cochran_1977-30] Jump up to: ^а ^{беременный} Кокран, Уильям Г. (1977). Методы отбора проб (третье изд.). Нью -Йорк: Джон Уайли и сыновья.

[31] Это впоследствии изложено в разделе генотипических дисперсий.

[32] Оба используются обычно.

[33] См. Предыдущие цитаты.

[Allard_1960-34] Аллард, RW (1960). Принципы размножения растений . Нью -Йорк: Джон Уайли и сыновья.

[varpq-35] Jump up to: ^а ^{беременный} Это читается как "σ ²_P и/или σ ²_Q ". Как P и Q дополняют, σ ²_P ≡ ≡ ²_Q и σ ²_P = σ ²_Q.

[Gordon_2003-36] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я Гордон, Иллинойс (2003). «Уточнения к разделению инбредной генотипической дисперсии» . Наследственность . 91 (1): 85–89. doi : 10.1038/sj.hdy.6800284 . PMID 12815457 .

[Wright_1951-37] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час ^я ^Дж Райт, Сьюолл (1951). «Генетическая структура популяций». Анналы евгеники . 15 (4): 323–354. doi : 10.1111/j.1469-1809.1949.tb02451.x . PMID 24540312 .

[38] Помните, что проблема Auto/Allo -Bygosity может возникнуть только для гомологичных аллелей (то есть A и A , или A и A ), а не для не -гомологичных аллелей ( A и A ), которые не могут иметь одинаковый аллель. источник .

[39] Обычно использовать «α», а не «β» для этой величины (например, в уже упоминавшихся ссылках). Последнее используется здесь, чтобы минимизировать любую путаницу с «А», которая часто встречается также в этих же уравнениях.

[M&J_1971-40] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Мазер, Кеннет; Джинкс, Джон Л. (1971). Биометрическая генетика . Тол. 26 (2 изд.). Лондон: Чепмен и Холл. С. 349–364. doi : 10.1038/hdy.1971.47 . ISBN 0-412-10220-x Полем PMID 5285746 . S2CID 46065232 . {{cite book}}: |journal= игнорируется ( помощь )

[41] В терминологии Мазер фракция перед буквой является частью ярлыка для компонента.

[42] В каждой строке этих уравнений компоненты представлены в одном и том же порядке. Следовательно, вертикальное сравнение компонентом дает определение каждого в различных формах. Таким образом, компоненты Mather были переведены в рыболовные символы: таким образом, облегчая их сравнение. Перевод также был получен формально. См. Гордон 2003.

[cov-43] Jump up to: ^а ^{беременный} Ковариация-это совместная вещество между двумя наборами данных. Подобно дисперсии, он основан на сумме перекрестных продуктов (SCP) вместо SS. Исходя из этого, ясно, что дисперсия - это всего лишь особая форма ковариации.

[Hayman_1960-44] Хейман, Би (1960). «Теория и анализ Креста Диалеля. III» . Генетика . 45 (2): 155–172. doi : 10.1093/Genetics/45.2.155 . PMC 1210041 . PMID 17247915 .

[45] Было отмечено, что когда p = q или когда d = 0 , β [= a+(qp) d] «уменьшается» до a . В таких обстоятельствах σ ²_A = σ ²_а - но только численно . Они все еще не стали единственной и той же идентичностью. Это было бы аналогичным Sequitur с тем, что было отмечено ранее для «отклонений замены», рассматриваемых как «доминирование» для генной модели.

[46] Вспомогательные цитаты уже даны в предыдущих разделах.

[47] Фишер отметил, что эти остатки возникли благодаря воздействию доминирования: но он воздерживался от их определения как «дисперсии доминирования». (См. Вышеизложенные цитаты.) Обратитесь к более ранним обсуждениям в настоящем документе.

[48] При рассмотрении происхождения терминов: Фишер также предложил слово «дисперсию» для этой меры изменчивости. См. Фишер (1999), с.311 и Фишер (1918).

[Snedecor_&_Cochran-49] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Snedecor, George W.; Кокран, Уильям Г. (1967). Статистические методы (шестой изд.). Эймс: издательство штата Айова Университет. ISBN 0-8138-1560-6 .

[Kendall_&_Stuart-50] Jump up to: ^а ^{беременный} ^в Кендалл, мг; Стюарт, А. (1958). Усовершенствованная теория статистики. Том 1 (2 -е изд.). Лондон: Чарльз Гриффин.

[51] Обычная практика не иметь подписки на экспериментальную дисперсию «ошибки».

[52] В биометрии это дисперсионное рационирование, в котором часть выражается как фракция целого: то есть коэффициент определения . Такие коэффициенты используются особенно в регрессионном анализе . Стандартизированной версией регрессионного анализа является анализ пути . Здесь стандартизация означает, что данные были впервые разделены на их собственные экспериментальные стандартные ошибки для объединения шкал для всех атрибутов. Это генетическое использование является еще одним важным появлением коэффициентов определения.

[Gordon_Byth_Balaam_1972-53] Гордон, Иллинойс; Byth, de; Balaam, LN (1972). «Разница коэффициентов наследуемости, оцененные по компонентам фенотипической дисперсии». Биометрия . 28 (2): 401–415. doi : 10.2307/2556156 . JSTOR 2556156 . PMID 5037862 .

[Dohm_2002-54] Дом, М.Р. (2002). «Оценки повторяемости не всегда устанавливают верхний предел на наследуемость» . Функциональная экология . 16 (2): 273–280. Bibcode : 2002fueco..16..273m . doi : 10.1046/j.1365-2435.2002.00621.x .

[Li_1977-55] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Ли, Чинг Чун (1977). Анализ пути - праймер (вторая печать с исправлениями изд.). Pacific Grove: Boxwood Press. ISBN 0-910286-40-x .

[56] квадратный корн их продукта

[Moroney_1956-57] Moroney, MJ (1956). Факты из цифр (третье изд.). Harmondsworth: книги пингвинов.

[Draper_&_Smith-58] Jump up to: ^а ^{беременный} Дрейпер, Норман Р.; Смит, Гарри (1981). Применяемый регрессионный анализ (второе изд.). Нью -Йорк: Джон Уайли и сыновья. ISBN 0-471-02995-5 .

[Balaam_1972-59] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Balaam, LN (1972). Основы биометрии . Лондон: Джордж Аллен и Unwin. ISBN 0-04-519008-9 .

[60] В прошлом обе формы ковариации родителей-скрещивания были применены к этой задаче оценки h ², но, как отмечалось в подразделе выше, только один из них ( COV (MPO) ) на самом деле уместен. Однако COV (PO) полезен для оценки H ² Как видно в основном тексте следующего.

[61] Обратите внимание, что тексты, которые игнорируют компонент доминирования COV (HS) ошибочно предполагают, что r _hs «приблизительно» ( ⁠ 1/4 ⁠ H ² ).

[62] Причард, Джонатан К.; Пикрелл, Джозеф К.; Куп, Грэм (23 февраля 2010 г.). «Генетика адаптации человека: жесткие зачистки, мягкие зачистки и полигенная адаптация» . Текущая биология . 20 (4): R208–215. Bibcode : 2010cbio ... 20.r208p . doi : 10.1016/j.cub.2009.11.055 . ISSN 1879-0445 . PMC 2994553 . PMID 20178769 .

[63] Турчин, Майкл С.; Чиан, Чарльстон, WK; Палмер, Кэмерон Д.; Sankararaman, Sriram; Рейх, Дэвид; Генетическое исследование консорциума антропометрических признаков (гигантских); Хиршхорн, Джоэл Н. (сентябрь 2012 г.). «Свидетельство широко распространенного отбора о изменении в Европе в SNP, связанных с высотой» . Природа генетика . 44 (9): 1015–1019. doi : 10.1038/ng.2368 . ISSN 1546-1718 . PMC 3480734 . PMID 22902787 .

[64] Берг, Джереми Дж.; Куп, Грэм (август 2014 г.). «Генетический сигнал популяции полигенной адаптации» . PLOS Genetics . 10 (8): E1004412. doi : 10.1371/journal.pgen.1004412 . ISSN 1553-7404 . PMC 4125079 . PMID 25102153 .

[65] Поле, яир; Бойл, Эван А.; Телис, Натали; Гао, Ziyue; Голтон, Кайл Дж.; Голан, Дэвид; Yengo, Loic; Рошело, Гислан; Froguel, Филипп (11 ноября 2016 г.). «Обнаружение адаптации человека в течение последних 2000 лет» . Наука . 354 (6313): 760–764. Bibcode : 2016sci ... 354..760f . doi : 10.1126/science.AAG0776 . ISSN 0036-8075 . PMC 5182071 . PMID 27738015 .

[66] Теоретически, хвост бесконечен , но на практике есть квази-энд .

[Becker_1967-67] Jump up to: ^а ^{беременный} Беккер, Уолтер А. (1967). Руководство по процедурам в количественной генетике (второе изд.). Пулман: Вашингтонский государственный университет.

[68] Обратите внимание, что это б ² является коэффициентом происхождения ( F _AA ) переписанного анализа родословного, с «уровнем генерации» вместо «A» внутри скобков.

[69] Есть небольшое «колебание», возникающее из -за того, что б ² изменяет одно поколение позади ²- Экспонируйте их уравнения инбридинга.

[70] Оценивается как квадратный корн их продукта.

[71] «Репродуктивная изоляция» . Понимание эволюции . Беркли. 16 апреля 2021 года.

[72] Serres-Armero, A; Дэвис, BW; Поволоцкая, есть; Morcillo-Suarez, C; Plassais, J; Хуан, D; Остранд, EA; Marques-Bonet, t (май 2021 г.). «Изменение числа копий лежит в основе сложных фенотипов у домашних пород собак и других Canids» . Исследование генома . 31 (5): 762–774. doi : 10.1101/gr.266049.120 . PMC 8092016 . PMID 33863806 .

[73] Цзян, Юэксин; Болник, Даниэль I.; Киркпатрик, Марк (2013). «Ассортативное спаривание у животных» (PDF) . Американский натуралист . 181 (6): E125 - E138. doi : 10.1086/670160 . HDL : 2152/31270 . PMID 23669548 . S2CID 14484725 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

v Т и Генетика : количественная генетика
Concepts in Quantitative Genetics	Heritability Dominance Quantitative trait locus Candidate gene Effective population size
Related Topics	Population genetics Genomics Evolutionary biology Heredity

v Т и Генетика
Introduction Outline History Timeline Index Glossary
Key components	Chromosome DNA RNA Genome Heredity Nucleotide Mutation Genetic variation Allele Amino acid
Fields	Classical Conservation Cytogenetics Ecological Immunogenetics Microbial Molecular Population Quantitative
Archaeogenetics of	Africa the Americas the British Isles Europe Italy the Middle East South Asia
Related topics	Behavioural genetics Epigenetics Geneticist Genome editing Genomics Genetic code Genetic engineering Genetic diversity Genetic monitoring Genetic genealogy Heredity He Jiankui affair Medical genetics Missing heritability problem Molecular evolution Plant genetics Population genomics Reverse genetics
Lists	List of genetic codes List of genetics research organizations
Category