Уравнение Нернста

В электрохимии уравнение Нернста представляет собой химическую термодинамическую зависимость, которая позволяет рассчитать восстановительный потенциал реакции ( реакции полуячейки или полной ячейки ) на основе стандартного электродного потенциала , абсолютной температуры , количества электронов, участвующих в окислительно-восстановительной реакции , и активность (часто аппроксимируемую концентрациями) химических веществ, подвергающихся восстановлению и окислению соответственно. Оно было названо в честь Вальтера Нернста , немецкого физико-химика, сформулировавшего это уравнение. ^{[ 1 ]}^{[ 2 ]}

Выражение

Общая форма с химической активностью

Когда окислитель ( $Ox$ ) принимает количество z электронов ( e ⁻) для преобразования в восстановленную форму ( $Red$ ), полуреакция выражается как:

{\ce {Ox + ze- -> Red}}

Коэффициент реакции ( $Q r$ ), также часто называемый продуктом активности иона ( IAP ), представляет собой соотношение между химической активностью ( a ) восстановленной формы ( восстановитель , $Red .$ ) и окисленной формы ( окислитель , $Ox)$ ). Химическая активность растворенного вещества соответствует его истинной термодинамической концентрации с учетом электрических взаимодействий между всеми ионами, присутствующими в растворе при повышенных концентрациях. Для данного растворенного вещества его химическая активность (а) представляет собой произведение его коэффициента активности (γ) на его молярную (моль/л раствора) или моляльную (моль/кг воды) концентрацию (C): a = γ C Таким образом, если концентрация ( C , также обозначенная здесь ниже квадратными скобками [ ]) всех интересующих растворенных веществ достаточно низка и их коэффициенты активности близки к единице, их химическая активность может быть аппроксимирована их концентрациями , как обычно. сделано при упрощении, или идеализация, реакция в дидактических целях:

Q_{r}={\frac {a_{\text{Red}}}{a_{\text{Ox}}}}={\frac {[\operatorname {Red} ]}{[\operatorname {Ox} ]}}

При химическом равновесии отношение $Q r$ активности продукта реакции ( a _Red ) к активности реагента ( a _Ox ) равно константе равновесия $K$ полуреакции:

K={\frac {a_{\text{Red}}}{a_{\text{Ox}}}}

Стандартная термодинамика также утверждает, что фактическая свободная энергия Гиббса $Δ G$ связана с изменением свободной энергии в стандартном состоянии $Δ G. тот$ по отношению: $\Delta G=\Delta G^{\ominus }+RT\ln Q_{r}$ где $Q r$ — коэффициент реакции , а R — универсальная постоянная идеального газа . Потенциал ячейки $E,$ связанный с электрохимической реакцией, определяется как уменьшение свободной энергии Гиббса на кулон переданного заряда, что приводит к соотношению $\Delta G=-zFE.$ Константа $F$ ( константа Фарадея ) — это коэффициент преобразования единиц $F = N A q$ , где $N A$ — постоянная Авогадро , а $q$ — основной заряд электрона . Это немедленно приводит к уравнению Нернста, которое для электрохимической полуячейки имеет вид $E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {a_{\text{Red}}}{a_{\text{Ox}}}}.$ Для полной электрохимической реакции (полная ячейка) уравнение можно записать как $E_{\text{cell}}=E_{\text{cell}}^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}$

где:

$E red$ полуячейки — потенциал восстановления при интересующей температуре,
$И тот красный$ — стандартный потенциал восстановления полуклеток ,
$E cell$ — это потенциал ячейки ( электродвижущая сила ) при интересующей температуре,
$И тот клетка$ – стандартный потенциал клетки ,
$R$ — универсальная постоянная идеального газа : $R = 8,314 46261815324 Дж. -1 моль -1$ ,
$Т$ — температура в Кельвинах ,
$z$ — число электронов, перенесённых в клеточной реакции или полуреакции ,
$F$ — постоянная Фарадея, величина заряда (в кулонах ) на моль электронов: $F = 96485,332 1233100184 Кл моль -1$ ,
$Q r$ - коэффициент реакции клетки, и
$a$ — химическая активность соответствующего вида, где $Red Ox$ — активность восстановленной формы, а $— активность$ окисленной формы.

Тепловое напряжение

При комнатной температуре (25 °C) тепловое напряжение $V_{T}={\frac {RT}{F}}$ составляет примерно 25,693 мВ. Уравнение Нернста часто выражается в виде логарифмов по основанию 10 ( т. е . десятичных логарифмов ), а не натуральных логарифмов , и в этом случае оно записывается:

$E=E^{\ominus }-{\frac {V_{T}}{z}}\ln {\frac {a_{\text{Red}}}{a_{\text{Ox}}}}=E^{\ominus }-{\frac {\lambda V_{T}}{z}}\log _{10}{\frac {a_{\text{Red}}}{a_{\text{Ox}}}}.$

где λ = ln(10) ≈ 2,3026 и λV _T ≈ 0,05916 Вольт.

Форма с коэффициентами активности и концентрациями

Подобно константам равновесия, активность всегда измеряется относительно стандартного состояния (1 моль/л для растворенных веществ, 1 атм для газов и T = 298,15 К, т. е . 25 °C или 77 °F). вида $i$ , $ai,$ связана $Ci концентрацией$ соотношением $ai . = γiCi Химическая активность с,$ где $γi —$ коэффициент активности вида $i$ измеренной Поскольку коэффициенты активности имеют тенденцию к единице при низких концентрациях или неизвестны или их трудно определить при средних и высоких концентрациях, активности в уравнении Нернста часто заменяются простыми концентрациями, а затем формальными стандартными потенциалами восстановления. $E_{\text{red}}^{\ominus '}$ использовал.

С учетом коэффициентов активности ( $\gamma$ ) уравнение Нернста принимает вид:

$E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln \left({\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}{\frac {C_{\text{Red}}}{C_{\text{Ox}}}}\right)$

$E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\left(\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}+\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}\right)$

$E_{\text{red}}=\underbrace {\left(E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}\right)} _{E_{\text{red}}^{\ominus '}}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}$

Где первый член, включающий коэффициенты активности ( $\gamma$ ) обозначается $E_{\text{red}}^{\ominus '}$ и назван формальным стандартным потенциалом приведения, так что $E_{\text{red}}$ может быть непосредственно выражено как функция $E_{\text{red}}^{\ominus '}$ и концентрации в простейшей форме уравнения Нернста:

$E_{\text{red}}=E_{\text{red}}^{\ominus '}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}$

Потенциал снижения формального стандарта

При желании использовать простые концентрации вместо активностей, но коэффициенты активности далеки от единицы и ими уже нельзя пренебрегать, они неизвестны или слишком трудно поддаются определению, может оказаться удобным ввести понятие «так называемого» стандартный потенциал формальной редукции ( $E_{\text{red}}^{\ominus '}$ ), что связано со стандартным потенциалом восстановления следующим образом: ^{[ 3 ]} $E_{\text{red}}^{\ominus '}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}$ Таким образом, уравнение Нернста для реакции полуячейки можно правильно формально записать через концентрации как: $E_{\text{red}}=E_{\text{red}}^{\ominus '}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}$ и аналогично для полноклеточной экспрессии.

По словам Венцеля (2020), ^{[ 4 ]} формальный потенциал сокращения $E_{\text{red}}^{\ominus '}$ представляет собой восстановительный потенциал, который применяется к полуреакции при наборе определенных условий, таких как, например, pH , ионная сила или концентрация комплексообразователей .

Формальный потенциал приведения $E_{\text{red}}^{\ominus '}$ часто является более удобной, но условной формой стандартного восстановительного потенциала, учитывающей коэффициенты активности и особенности конкретных условий реакционной среды. Поэтому ее значение является величиной условной, т. е . зависит от условий эксперимента и от того, что ионная сила влияет на коэффициенты активности, $E_{\text{red}}^{\ominus '}$ будет варьироваться от среднего до среднего. ^{[ 3 ]} В литературе можно найти несколько определений формального потенциала приведения в зависимости от преследуемой цели и экспериментальных ограничений, налагаемых изучаемой системой. Общее определение $E_{\text{red}}^{\ominus '}$ относится к его значению, определенному, когда ${\frac {C_{\text{red}}}{C_{\text{ox}}}}=1$ . Более частный случай — когда $E_{\text{red}}^{\ominus '}$ также определяется при pH 7, например, для окислительно-восстановительных реакций, важных в биохимии или биологических системах.

Определение формального стандартного потенциала сокращения, когда $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ C red / C ox ⁠$ = 1

Потенциал снижения формального стандарта $E_{\text{red}}^{\ominus '}$ может быть определен как измеренный потенциал восстановления $E_{\text{red}}$ полуреакции при соотношении концентраций окисленных и восстановленных частиц, равном единице ( т.е. когда $⁠ C red / C ox ⁠$ = 1) при данных условиях. ^{[ 5 ]}

Действительно:

как, $E_{\text{red}}=E_{\text{red}}^{\ominus }$ , когда ${\frac {a_{\text{red}}}{a_{\text{ox}}}}=1$ ,

E_{\text{red}}=E_{\text{red}}^{\ominus '}

, когда

{\frac {C_{\text{red}}}{C_{\text{ox}}}}=1

,

потому что $\ln {1}=0$ , и что термин ${\frac {\gamma _{\text{red}}}{\gamma _{\text{ox}}}}$ включен в $E_{\text{red}}^{\ominus '}$ .

Формальный потенциал восстановления позволяет проще работать с молярными (моль/л, М) или моляльными (моль/кг) H ₂ O , м) концентрации в месте деятельности . Поскольку молярные и моляльные концентрации когда-то назывались формальными концентрациями , это могло объяснить происхождение прилагательного «формальный» в выражении «формальный потенциал». ^{[ нужна ссылка ]}

Таким образом, формальный потенциал — это обратимый потенциал равновесного электрода, погруженного в раствор, в котором реагенты и продукты имеют единичную концентрацию. ^{[ 6 ]} Если любое небольшое постепенное изменение потенциала вызывает изменение направления реакции, т. е. от восстановления к окислению или наоборот , система близка к равновесию, обратима и находится при своем формальном потенциале. Когда формальный потенциал измеряется в стандартных условиях ( т.е. активность каждого растворенного вещества составляет 1 моль/л, T = 298,15 K = 25 °C = 77 °F, $P газ$ = 1 бар), он становится де-факто стандартным потенциалом. ^{[ 7 ]}
По словам Брауна и Свифта (1949):

«Формальный потенциал определяется как потенциал полуэлемента, измеренный относительно стандартного водородного электрода , когда общая концентрация каждой степени окисления равна одной формальной ». ^{[ 8 ]}

В этом случае, что касается стандартных потенциалов восстановления, концентрации растворенных частиц остаются равными одному молярному (М) или одному моляльному (м), и поэтому называются формальным (F). Итак, выразив концентрацию $С$ в молярности $М$ (1 моль/л):

{\frac {C_{\text{red}}}{C_{\text{ox}}}}={\frac {1\,\mathrm {M} _{\text{red}}}{1\,\mathrm {M} _{\text{ox}}}}=1

Термин «формальная концентрация» (F) в настоящее время в значительной степени игнорируется в современной литературе и обычно может быть отождествлен с молярной концентрацией (M) или моляльностью (m) в случае термодинамических расчетов. ^{[ 9 ]}

Формальный потенциал также находится на полпути между двумя пиками циклической вольтамперограммы , где в этот момент концентрации Ox (окисленных частиц) и Red (восстановленных частиц) на поверхности электрода равны.

Коэффициенты активности $\gamma _{red}$ и $\gamma _{ox}$ входят в формальный потенциал $E_{\text{red}}^{\ominus '}$ и поскольку они зависят от условий эксперимента, таких как температура, ионная сила и pH , $E_{\text{red}}^{\ominus '}$ нельзя назвать неизменным стандартным потенциалом, но его необходимо систематически определять для каждого конкретного набора экспериментальных условий. ^{[ 7 ]}

Формальные редукционные потенциалы применяются для упрощения расчетов рассматриваемой системы в заданных условиях и интерпретации измерений. Условия эксперимента, в которых они определяются, и их связь со стандартными потенциалами восстановления должны быть четко описаны, чтобы не спутать их со стандартными потенциалами восстановления.

Формальный стандартный потенциал восстановления при pH 7

Формальные стандартные потенциалы восстановления ( $E_{\text{red}}^{\ominus '}$ ) также широко используются в биохимии и клеточной биологии для обозначения стандартных потенциалов восстановления, измеренных при pH 7, значении, более близком к pH большинства физиологических и внутриклеточных жидкостей, чем стандартное состояние pH, равное 0. Преимущество состоит в определении более подходящего окислительно-восстановительного потенциала. масштаб лучше соответствует реальным условиям, чем стандартное состояние. Формальные стандартные потенциалы восстановления ( $E_{\text{red}}^{\ominus '}$ ) позволяют более легко оценить, осуществима или нет окислительно-восстановительная реакция, которая, как предполагается, происходит в метаболическом процессе или стимулирует микробную активность при некоторых условиях.

В то время как стандартные потенциалы восстановления всегда относятся к стандартному водородному электроду (SHE), где [ H ⁺] = 1 М, что соответствует pH 0, и $E_{\text{red H+}}^{\ominus }$ по соглашению произвольно зафиксировано равным нулю, это уже не так при pH 7. Тогда потенциал восстановления $E_{\text{red}}$ водородного электрода, работающего при pH 7, составляет -0,413 В по отношению к стандартному водородному электроду (СТЭ). ^{[ 10 ]}

Выражение уравнения Нернста в зависимости от pH

The $E_{h}$ и pH раствора связаны уравнением Нернста, которое обычно представляется диаграммой Пурбе ( $E_{h}$ – pH график ) . $E_{h}$ явно обозначает $E_{\text{red}}$ выражается по сравнению со стандартным водородным электродом (SHE). Для уравнения полуячейки , условно записанного как реакция восстановления ( т. е . электроны, принятые окислителем с левой стороны):

a\,A+b\,B+h\,{\ce {H+}}+z\,e^{-}\quad {\ce {<=>}}\quad c\,C+d\,D

полуклетки Потенциал восстановления стандарта $E_{\text{red}}^{\ominus }$ дается

E_{\text{red}}^{\ominus }({\text{volt}})=-{\frac {\Delta G^{\ominus }}{zF}}

где $\Delta G^{\ominus }$ — стандартное изменение свободной энергии Гиббса , $z$ — количество вовлеченных электронов, а $F$ — постоянная Фарадея . Уравнение Нернста связывает pH и $E_{h}$ следующее:

E_{h}=E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {0.05916}{z}}\log \left({\frac {\{C\}^{c}\{D\}^{d}}{\{A\}^{a}\{B\}^{b}}}\right)-{\frac {0.05916\,h}{z}}{\text{pH}}

^{[ нужна ссылка ]}

где фигурные скобки обозначают активности , а показатели степени показаны обычным способом. Это уравнение представляет собой уравнение прямой для $E_{\text{red}}$ в зависимости от pH с наклоном $-0.05916\,\left({\frac {h}{z}}\right)$ вольт (у pH нет единиц измерения).

Это уравнение предсказывает более низкую $E_{\text{red}}$ при более высоких значениях pH. Это наблюдается при восстановлении O ₂ до H ₂ O, или OH ⁻, а для уменьшения H ⁺ в Н ₂ . $E_{\text{red}}$ тогда часто отмечают как $E_{h}$ чтобы указать, что речь идет о стандартном водородном электроде (SHE), чей $E_{\text{red}}$ = 0 условно в стандартных условиях (T = 298,15 K = 25 ° C = 77 F, _газ P = 1 атм (1,013 бар), концентрации = 1 M и, следовательно, pH = 0).

Основные факторы, влияющие на потенциал снижения формальных стандартов

Основным фактором, влияющим на формальные восстановительные потенциалы в биохимических или биологических процессах, чаще всего является pH. Чтобы определить приблизительные значения формальных потенциалов восстановления, пренебрегая в первом подходе изменениями коэффициентов активности, обусловленными ионной силой, необходимо применить уравнение Нернста, стараясь сначала выразить зависимость как функцию pH. Вторым фактором, который необходимо учитывать, являются значения концентраций, учитываемых в уравнении Нернста. Чтобы определить формальный потенциал восстановления биохимической реакции, всегда необходимо явно указывать значение pH, значения концентраций и гипотезы, сделанные в отношении коэффициентов активности. При использовании или сравнении нескольких формальных потенциалов приведения они также должны быть внутренне непротиворечивыми.

Проблемы могут возникнуть при смешивании разных источников данных с использованием разных соглашений или приближений ( т. е. с разными базовыми гипотезами). При работе на границе между неорганическими и биологическими процессами (например, при сравнении абиотических и биотических процессов в геохимии, когда микробная активность также может действовать в системе), необходимо соблюдать осторожность, чтобы случайно не смешать стандартные восстановительные потенциалы с SHE (pH). = 0) с формальными восстановительными потенциалами (pH = 7). Определения должны быть четко выражены и тщательно контролироваться, особенно если источники данных различны и происходят из разных областей (например, сбор и смешивание данных из классических учебников по электрохимии и микробиологии без учета различных соглашений, на которых они основаны).

Примеры с диаграммой Пурбе

Диаграмма Пурбе для воды, включая области стабильности воды, кислорода и водорода при стандартной температуре и давлении (STP). Вертикальная шкала (ордината) представляет собой потенциал электрода относительно электрода СТЭ . Горизонтальная шкала (по оси абсцисс) — pH электролита (в противном случае невзаимодействующего). Выше верхней линии кислород будет выходить из электрода до тех пор, пока вода не будет полностью израсходована. Аналогичным образом, ниже нижней линии водород будет пузыриться с электрода до тех пор, пока вода не будет полностью израсходована.

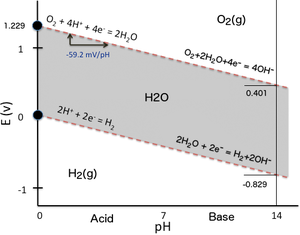
Чтобы проиллюстрировать зависимость восстановительного потенциала от pH, можно просто рассмотреть два окислительно-восстановительных равновесия, определяющих область стабильности воды, на диаграмме Пурбе (график E _h – pH) . Когда вода подвергается электролизу путем приложения достаточной разницы электрических потенциалов между двумя электродами , погруженными в воду, водород образуется на катоде (восстановление протонов воды), а кислород образуется на аноде (окисление атомов кислорода воды). То же самое может произойти, если восстановитель, более сильный, чем водород (например, металлический Na) или окислитель, более сильный, чем кислород (например, F ₂ ), вступит в контакт с водой и вступит с ней в реакцию. На приведенном ниже графике E _h –pH (самая простая возможная версия диаграммы Пурбе) область стабильности воды (серая поверхность) ограничена с точки зрения окислительно-восстановительного потенциала двумя наклонными красными пунктирными линиями:

Линия нижней стабильности с выделением газообразного водорода из-за восстановления протонов при очень низких E _h :

2 часа + + 2 и - ⇌ H 2

(катод: восстановление)

Линия более высокой стабильности с выделением газообразного кислорода вследствие окисления кислорода в воде при очень высоком E _h :

2 Н 2 О ⇌ О 2 + 4 Н + + 4 и -

(анод: окисление)

При решении уравнения Нернста для каждой соответствующей реакции восстановления (необходимо обратить вспять реакцию окисления воды с образованием кислорода) оба уравнения имеют схожий вид, поскольку количество протонов и количество электронов, участвующих в реакции, одинаковы, а их соотношение равно единице. (2 часа ⁺/2 е ⁻ для H ₂ и 4 H ⁺/4 е ⁻ с O ₂ соответственно), поэтому упрощается решение уравнения Нернста, выраженного как функция рН.

Результат можно выразить численно следующим образом:

E_{\text{red}}=E_{\text{red}}^{\ominus }-0.05916\ pH

Обратите внимание, что наклоны верхней и нижней линий двух областей стабильности воды одинаковы (единицы -59,16 мВ/pH), поэтому на диаграмме Пурбе они параллельны . Поскольку наклоны отрицательные, при высоком pH выделение как водорода, так и кислорода требует гораздо меньшего восстановительного потенциала, чем при низком pH.

Для снижения H ⁺ в H ₂ вышеупомянутое соотношение становится:

E_{\text{red}}=-0.05916\ pH

потому что по соглашению

E_{\text{red}}^{\ominus }

= 0 В для стандартного водородного электрода (SHE: pH = 1).
Итак, при pH = 7,

E_{\text{red}}

= -0,414 В для восстановления протонов.

Для восстановления O ₂ до 2 H ₂ O вышеупомянутое соотношение принимает вид:

E_{\text{red}}=1.229-0.05916\ pH

потому что

E_{\text{red}}^{\ominus }

= +1,229 В относительно стандартного водородного электрода (СТЭ: pH = 1).
Итак, при pH = 7,

E_{\text{red}}

= +0,815 В для восстановления кислорода.

Смещение -414 мВ в $E_{\text{red}}$ одинаков для обеих реакций восстановления, поскольку они имеют одну и ту же линейную зависимость в зависимости от pH и наклоны их линий одинаковы. Это можно непосредственно проверить на диаграмме Пурбе. Для других реакций восстановления величина формального потенциала восстановления при pH 7, обычно называемая биохимическими реакциями, также зависит от наклона соответствующей линии на диаграмме Пурбе, т.е. от соотношения h ⁄ z числа H ⁺ к числу е ⁻ участвует в реакции восстановления и, следовательно, влияет на стехиометрию полуреакции. Таким образом, определение формального потенциала восстановления при pH = 7 для данной биохимической полуреакции требует расчета его с помощью соответствующего уравнения Нернста в зависимости от pH. Нельзя просто применить смещение -414 мВ к значению E _h (SHE), когда соотношение h / z отличается от 1.

Приложения в биологии

Помимо важных окислительно-восстановительных реакций в биохимии и микробиологии , уравнение Нернста используется также в физиологии для расчета электрического потенциала клеточной мембраны по отношению к одному типу ионов . Его можно связать с константой диссоциации кислоты .

Нернст потенциал

Уравнение Нернста имеет физиологическое применение, когда оно используется для расчета потенциала иона с зарядом $z$ через мембрану. Этот потенциал определяется по концентрации иона как внутри, так и снаружи клетки:

$E={\frac {RT}{zF}}\ln {\frac {[{\text{ion outside cell}}]}{[{\text{ion inside cell}}]}}=2.3026{\frac {RT}{zF}}\log _{10}{\frac {[{\text{ion outside cell}}]}{[{\text{ion inside cell}}]}}.$

Когда мембрана находится в термодинамическом равновесии (т. е. нет чистого потока ионов) и если клетка проницаема только для одного иона, то мембранный потенциал должен быть равен потенциалу Нернста для этого иона.

Уравнение Гольдмана

Когда мембрана проницаема для более чем одного иона, что неизбежно происходит, потенциал покоя можно определить из уравнения Гольдмана, которое представляет собой решение уравнения притока GHK при условии, что общая плотность тока, вызванная электрохимической силой, равна нулю:

$E_{\mathrm {m} }={\frac {RT}{F}}\ln {\left({\frac {\displaystyle \sum _{i}^{N}P_{\mathrm {M} _{i}^{+}}\left[\mathrm {M} _{i}^{+}\right]_{\mathrm {out} }+\displaystyle \sum _{j}^{M}P_{\mathrm {A} _{j}^{-}}\left[\mathrm {A} _{j}^{-}\right]_{\mathrm {in} }}{\displaystyle \sum _{i}^{N}P_{\mathrm {M} _{i}^{+}}\left[\mathrm {M} _{i}^{+}\right]_{\mathrm {in} }+\displaystyle \sum _{j}^{M}P_{\mathrm {A} _{j}^{-}}\left[\mathrm {A} _{j}^{-}\right]_{\mathrm {out} }}}\right)},$

где

$Em —$ мембранный потенциал (в вольтах , что эквивалентно джоулям на кулон ),
$P ion$ — проницаемость для этого иона (в метрах в секунду),
$[ion] out$ — это внеклеточная концентрация этого иона (в молях на кубический метр, чтобы соответствовать другим единицам СИ , хотя единицы строго не имеют значения, поскольку термины концентрации ионов становятся безразмерным отношением),
$[ion] in$ — внутриклеточная концентрация этого иона (в молях на кубический метр),
$R$ — постоянная идеального газа (джоули на кельвин на моль),
$Т$ — температура в Кельвинах ,
$F$ — постоянная Фарадея (кулоны на моль).

Потенциал через клеточную мембрану, который точно препятствует чистой диффузии определенного иона через мембрану, называется потенциалом Нернста для этого иона. Как видно выше, величина потенциала Нернста определяется соотношением концентраций этого конкретного иона по обе стороны мембраны. Чем больше это отношение, тем больше тенденция иона к диффузии в одном направлении и, следовательно, тем больший потенциал Нернста требуется для предотвращения диффузии. Существует аналогичное выражение, включающее $r$ (абсолютное значение коэффициента переноса). При этом учитываются перевозчики с неравноценным обменом. См.: Натриево-калиевый насос , где коэффициент переноса будет 2/3, поэтому в формуле ниже r равно 1,5. Причина, по которой мы вставляем здесь коэффициент r = 1,5, заключается в том, что плотность тока под действием электрохимической силы J _e.c. (На ⁺) + J _э.к. (К ⁺) уже не равен нулю, а скорее J _e.c. (На ⁺) + 1,5 Дж _{и т. д.} (К ⁺) = 0 (поскольку поток обоих ионов за счет электрохимической силы компенсируется потоком насосов, т. е. J _e.c. = −J _pump ), изменяя ограничения для применения уравнения GHK. Остальные переменные такие же, как указано выше. Следующий пример включает два иона: калий (K ⁺) и натрий (Na ⁺). Предполагается, что хлорид находится в равновесии. $E_{m}={\frac {RT}{F}}\ln {\left({\frac {rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {out} }}{rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {in} }}}\right)}.$

Когда хлорид (Cl ⁻) учитывается,

$E_{m}={\frac {RT}{F}}\ln {\left({\frac {rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Cl} ^{-}}\left[\mathrm {Cl} ^{-}\right]_{\mathrm {in} }}{rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Cl} ^{-}}\left[\mathrm {Cl} ^{-}\right]_{\mathrm {out} }}}\right)}.$

Вывод

Использование фактора Больцмана

Для простоты будем рассматривать раствор редокс-активных молекул, вступающих в одноэлектронную обратимую реакцию.

Ох + е - ⇌ Красный

и которые имеют стандартный нулевой потенциал и в которых активность хорошо представлена концентрациями (т.е. единичным коэффициентом активности). Химический потенциал $ц рабочему$ этого раствора представляет собой разность энергетических барьеров отвода и отдачи электронов к электроду раствора , задающему электрохимический потенциал . Отношение окисленных к восстановленным молекулам, ⁠ [Ox] / [Red] ⁠ эквивалентно вероятности окисления (отдачи электронов) над вероятностью восстановления (захвата электронов), которую мы можем записать через фактор Больцмана для этих процессов: ${\begin{aligned}{\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}&={\frac {\exp \left(-[{\text{barrier for gaining an electron}}]/kT\right)}{\exp \left(-[{\text{barrier for losing an electron}}]/kT\right)}}\\[6px]&=\exp \left({\frac {\mu _{\mathrm {c} }}{kT}}\right).\end{aligned}}$

Взяв натуральный логарифм обеих частей, получим $\mu _{\mathrm {c} }=kT\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.$

Если $µ c \neq 0$ при ⁠ [Ox] / [Red] ⁠ = 1, нам нужно добавить эту дополнительную константу: $\mu _{\mathrm {c} }=\mu _{\mathrm {c} }^{\ominus }+kT\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.$

Разделив уравнение на $e,$ чтобы преобразовать химические потенциалы в электродные потенциалы, и помнить, что $⁠ k / e ⁠ = ⁠ R / F ⁠$ , ^{[ 11 ]} получим уравнение Нернста для одноэлектронного процесса $Ox + e - ⇌ Красный$ :

${\begin{aligned}E&=E^{\ominus }-{\frac {kT}{e}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{F}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.\end{aligned}}$

Использование термодинамики (химического потенциала)

Количества здесь даны на молекулу, а не на моль , поэтому используются константа Больцмана $k$ и заряд электрона $e$ вместо газовой постоянной $R$ и постоянной Фарадея $F$ . приведенные в большинстве учебников по химии, необходимо просто умножить на константу Авогадро : $R = kN A$ и $F = eN A.$ Для перевода в мольные количества , Энтропия молекулы определяется как

$S\ {\stackrel {\mathrm {def} }{=}}\ k\ln \Omega ,$

где $Ω$ — число состояний, доступных молекуле. Число состояний должно изменяться линейно в зависимости от объема $V$ системы (здесь для лучшего понимания рассматривается идеализированная система, так что активности предполагаются очень близкими к истинным концентрациям. Фундаментальное статистическое доказательство упомянутой линейности выходит за рамки этой статьи). раздел, но чтобы убедиться в этом, проще рассмотреть обычный изотермический процесс для идеального газа , где изменение энтропии $Δ S = nR ln(⁠ V 2 / V 1 ⁠)$ имеет место. Из определения энтропии и условия постоянства температуры и количества газа $n$ следует , что изменение числа состояний должно быть пропорционально относительному изменению объема $⁠ В 2 / В 1 ⁠$ . В этом смысле нет никакой разницы в статистических свойствах атомов идеального газа по сравнению с растворенными видами раствора с коэффициентами активности , равными единице: частицы свободно «болтаются», заполняя предоставленный объем), что обратно пропорционально концентрации с $,$ так мы также можем записать энтропию как $S=k\ln \ (\mathrm {constant} \times V)=-k\ln \ (\mathrm {constant} \times c).$

Таким образом, изменение энтропии от некоторого состояния 1 к другому состоянию 2 равно $\Delta S=S_{2}-S_{1}=-k\ln {\frac {c_{2}}{c_{1}}},$ так что энтропия состояния 2 равна $S_{2}=S_{1}-k\ln {\frac {c_{2}}{c_{1}}}.$

Если состояние 1 соответствует стандартным условиям, в которых $c 1$ равно единице (например, 1 атм или 1 М), оно просто отменит единицы $c 2$ . Поэтому мы можем записать энтропию произвольной молекулы A как $S(\mathrm {A} )=S^{\ominus }(\mathrm {A} )-k\ln[\mathrm {A} ],$ где $S^{\ominus }$ - энтропия в стандартных условиях , а [A] обозначает концентрацию A. Изменение энтропии реакции

а

А +

б

В →

y

Y +

z

Z

затем дается $\Delta S_{\mathrm {rxn} }={\big (}yS(\mathrm {Y} )+zS(\mathrm {Z} ){\big )}-{\big (}aS(\mathrm {A} )+bS(\mathrm {B} ){\big )}=\Delta S_{\mathrm {rxn} }^{\ominus }-k\ln {\frac {[\mathrm {Y} ]^{y}[\mathrm {Z} ]^{z}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}}.$

Мы определяем соотношение в последнем члене как коэффициент реакции : $Q_{r}={\frac {\displaystyle \prod _{j}a_{j}^{\nu _{j}}}{\displaystyle \prod _{i}a_{i}^{\nu _{i}}}}\approx {\frac {[\mathrm {Z} ]^{z}[\mathrm {Y} ]^{y}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}},$ где числитель представляет собой произведение активностей продуктов реакции $a j$ , возведенных в степень стехиометрического коэффициента ν $j,$ а знаменатель представляет собой аналогичный продукт активностей реагентов. Все действия относятся к моменту времени $t$ . При определенных обстоятельствах (см. химическое равновесие ) каждый термин активности, такой $как ν j j$ может быть заменен термином концентрации, [A]. В электрохимической ячейке потенциал ячейки $E$ представляет собой химический потенциал, доступный в результате окислительно-восстановительных реакций ( $E = ⁠ μ c / e ⁠$ ). $E$ связана с свободной энергии Гиббса изменением $Δ G$ только константой: $Δ G = - zFE$ , где $n$ — число переданных электронов, а $F$ — постоянная Фарадея . Знак отрицательный, поскольку спонтанная реакция имеет отрицательную энергию Гиббса $и ΔG$ положительный потенциал $E.$ свободную Свободная энергия Гиббса связана с энтропией соотношением $G = H - TS$ , где $H$ — энтальпия , а $T$ — температура системы. Используя эти соотношения, мы теперь можем записать изменение свободной энергии Гиббса: $\Delta G=\Delta H-T\Delta S=\Delta G^{\ominus }+kT\ln Q_{r},$ и потенциал клетки, $E=E^{\ominus }-{\frac {kT}{ze}}\ln Q_{r}.$

Это более общая форма уравнения Нернста.

Для окислительно-восстановительной реакции Ox + $z$ e ⁻ → Красный , $Q_{r}={\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}},$ и у нас есть: ${\begin{aligned}E&=E^{\ominus }-{\frac {kT}{ze}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{zF}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}.\end{aligned}}$

Потенциал ячейки при стандартной температуре и давлении (STP) $E^{\ominus }$ часто заменяется формальным потенциалом $E^{\ominus '}$ , который включает коэффициенты активности растворенных веществ в данных экспериментальных условиях (T, P, ионная сила , pH и комплексообразователи) и представляет собой потенциал, который фактически измеряется в электрохимической ячейке.

Связь с химическим равновесием

Стандартная свободная энергия Гиббса. $\Delta G^{\ominus }$ связана с константой равновесия $K$ следующим образом: ^{[ 12 ]}

\Delta G^{\ominus }=-RT\ln {K}

В то же время, $\Delta G^{\ominus }$ также равен произведению полного заряда ( $zF$ ), перенесенного в ходе реакции, на потенциал ячейки ( $E_{cell}^{\ominus }$ ):

\Delta G^{\ominus }=-zFE_{cell}^{\ominus }

Знак отрицательный, поскольку рассматриваемая система совершает работу и при этом выделяет энергию.

Так,

-zFE_{cell}^{\ominus }=-RT\ln {K}

И поэтому:

E_{cell}^{\ominus }={\frac {RT}{zF}}\ln {K}

Исходя из уравнения Нернста, ту же зависимость можно продемонстрировать и обратным способом.

При химическом равновесии или термодинамическом равновесии электрохимический потенциал $(E) = 0$ , следовательно, реакции ( $Qr коэффициент$ ) достигает особого значения, известного как константа равновесия ( $Keq и$ ):

Q р = К экв

Поэтому,

${\begin{aligned}0&=E^{\ominus }-{\frac {RT}{zF}}\ln K\\{\frac {RT}{zF}}\ln K&=E^{\ominus }\\\ln K&={\frac {zFE^{\ominus }}{RT}}\end{aligned}}$

Или в стандартном состоянии ,

$\log _{10}K={\frac {zE^{\ominus }}{\lambda V_{T}}}={\frac {zE^{\ominus }}{0.05916{\text{ V}}}}\quad {\text{at }}T=298.15~{\text{K}}$

Таким образом, мы связали стандартный электродный потенциал и константу равновесия окислительно-восстановительной реакции.

Ограничения

В разбавленных растворах уравнение Нернста можно выразить непосредственно через концентрации (поскольку коэффициенты активности близки к единице). Но при более высоких концентрациях необходимо использовать истинную активность ионов. Это усложняет использование уравнения Нернста, поскольку оценка неидеальных активностей ионов обычно требует экспериментальных измерений. Уравнение Нернста также применимо только тогда, когда через электрод нет чистого тока. Активность ионов на поверхности электрода изменяется при протекании тока , и существуют дополнительные члены перенапряжения и резистивные потери, которые вносят вклад в измеряемый потенциал.

При очень низких концентрациях потенциалопределяющих ионов потенциал, предсказываемый уравнением Нернста, приближается к $\pm\infty$ . Это физически бессмысленно, поскольку в таких условиях плотность тока обмена становится очень низкой и может отсутствовать термодинамическое равновесие, необходимое для выполнения уравнения Нернста. В таком случае электрод называют неуравновешенным. Другие эффекты имеют тенденцию брать под контроль электрохимическое поведение системы, например, участие сольватированного электрона в переносе электричества и электродном равновесии, как анализировали Александр Фрумкин и Б. Дамаскин. ^{[ 13 ]} Серджио Трасатти и др.

Зависимость потенциала от времени

Выражение зависимости от времени было установлено Караоглановым. ^{[ 14 ]}^{[ 15 ]}^{[ 16 ]}^{[ 17 ]}

Значение в других научных областях

Уравнение Нернста было вовлечено в научные споры о холодном синтезе . Флейшманн и Понс, утверждая, что холодный синтез может существовать, рассчитали, что палладиевый катод , погруженный в электролизную ячейку с тяжелой водой, может достичь температуры до 10 ²⁷ атмосферы давления внутри кристаллической решетки металла катода, достаточного для того, чтобы вызвать самопроизвольный ядерный синтез . В действительности было достигнуто всего 10 000–20 000 атмосфер. Американский физик Джон Р. Хьюзенга заявил, что на их первоначальные расчеты повлияла неверная интерпретация уравнения Нернста. ^{[ 18 ]} Он процитировал статью о сплавах Pd–Zr. ^{[ 19 ]}

Уравнение Нернста позволяет рассчитать степень реакции между двумя окислительно-восстановительными системами и может использоваться, например, для оценки того, завершится ли конкретная реакция или нет. При химическом равновесии электродвижущие силы (ЭДС) двух полуэлементов равны. Это позволяет рассчитать константу равновесия $K$ реакции и, следовательно, степень реакции.

См. также

Ссылки

^ Орна, Мэри Вирджиния; Сток, Джон (1989). Электрохимия в прошлом и настоящем . Колумбус, Огайо: Американское химическое общество. ISBN 978-0-8412-1572-6 . OCLC 19124885 .
^ Валь (2005). «Краткая история электрохимии». Гальванотехник . 96 (8): 1820–1828.
^ Jump up to: ^а ^б Бард, Аллен Дж.; Фолкнер, Ларри Р. (2001). «Глава 2. Потенциалы и термодинамика клеток - см.: 2.1.6 Формальные потенциалы». Электрохимические методы: Основы и приложения (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. п. 52.
^ Венцель, Томас (09.06.2020). «4. Таблица стандартных электрохимических потенциалов» . Химия LibreTexts . Проверено 24 ноября 2021 г.
^ Кано, Кенджи (2002). «Окислительно-восстановительные потенциалы белков и других соединений, представляющих биоэлектрохимический интерес, в водных растворах» . Обзор полярографии . 48 (1): 29–46. doi : 10.5189/revpolarography.48.29 . eISSN 1884-7692 . ISSN 0034-6691 . Проверено 2 декабря 2021 г.
^ «Формальный потенциал» . TheFreeDictionary.com . Проверено 6 декабря 2021 г.
^ Jump up to: ^а ^б ПалмСенс (2021). «Происхождение электрохимических потенциалов — PalmSens» . ПалмСенс . Проверено 6 декабря 2021 г.
^ Браун, Раймонд А.; Свифт, Эрнест Х. (1949). «Формальный потенциал сурьмяно-сурьмяной полуклетки в растворах соляной кислоты». Журнал Американского химического общества . 71 (8): 2719–2723. ISSN 0002-7863 . Цитата : Формальный потенциал определяется как потенциал полуэлемента, измеренный относительно стандартного водородного электрода, когда общая концентрация каждой степени окисления равна одной формальной.
^ Харви, Дэвид (15 июня 2020 г.). «2.2: Концентрация» . Химия LibreTexts . Проверено 15 декабря 2021 г.
^ Воэт, Дональд; Воэт, Джудит Г.; Пратт, Шарлотта В. (2016). «Таблица 14-4. Стандартные потенциалы восстановления для некоторых полуреакций биохимического импорта» . Основы биохимии: жизнь на молекулярном уровне (5-е изд.). Уайли. п. 466. ИСБН 978-1-118-91840-1 .
^ $р знак равно N А k$ ; см . газовую постоянную
$F знак равно N А е$ ; см . постоянную Фарадея
^ «20.5: Энергия Гиббса и окислительно-восстановительные реакции» . Химия LibreTexts . 18 ноября 2014 г. Проверено 6 декабря 2021 г.
^ Дж. Электроанал. хим. , 79 (1977), 259-266
^ Караогланов, З. (январь 1906 г.), «О процессах окисления и восстановления при электролизе растворов солей железа» , Журнал электрохимии (на немецком языке), 12 (1): 5–16, doi : 10.1002/bbpc.19060120105
^ Бард, Аллен Дж.; Инзельт, Дьёрдь; Шольц, Фриц, ред. (2012-10-02), «Уравнение Караогланова», Электрохимический словарь , Springer, стр. 527–528, ISBN 9783642295515
^ Зутши, Камала (2008), Введение в полярографию и смежные методы , стр. 127–128, ISBN 9788122417913
^ Журнал физической химии . Корнелльский университет. 1906.
^ Хуйзенга, Джон Р. (1993). Холодный синтез: научное фиаско века (2-е изд.). Оксфорд и Нью-Йорк: Издательство Оксфордского университета. стр. 33, 47. ISBN. 978-0-19-855817-0 .
^ Хуот, JY (1989). «Электролитическое гидрирование и аморфизация сплавов Pd-Zr». Журнал Электрохимического общества . 136 (3): 630–635. дои : 10.1149/1.2096700 . ISSN 0013-4651 .

Внешние ссылки

Симулятор уравнений Нернста/Гольдмана
Калькулятор уравнений Нернста
Интерактивный Java-апплет Nernst/Goldman
Пакет преподавания и обучения DoITPoMS - «Уравнение Нернста и диаграммы Пурбе»
«20.5: Энергия Гиббса и окислительно-восстановительные реакции» . Химия LibreTexts . 18 ноября 2014 г. Проверено 6 декабря 2021 г.

[isbn0-8412-1572-3-1] Орна, Мэри Вирджиния; Сток, Джон (1989). Электрохимия в прошлом и настоящем . Колумбус, Огайо: Американское химическое общество. ISBN 978-0-8412-1572-6 . OCLC 19124885 .

[Wahl2005-2] Валь (2005). «Краткая история электрохимии». Гальванотехник . 96 (8): 1820–1828.

[Bard_Faultner-3] Jump up to: ^а ^б Бард, Аллен Дж.; Фолкнер, Ларри Р. (2001). «Глава 2. Потенциалы и термодинамика клеток - см.: 2.1.6 Формальные потенциалы». Электрохимические методы: Основы и приложения (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. п. 52.

[Wenzel_2020-4] Венцель, Томас (09.06.2020). «4. Таблица стандартных электрохимических потенциалов» . Химия LibreTexts . Проверено 24 ноября 2021 г.

[Kano_2002-5] Кано, Кенджи (2002). «Окислительно-восстановительные потенциалы белков и других соединений, представляющих биоэлектрохимический интерес, в водных растворах» . Обзор полярографии . 48 (1): 29–46. doi : 10.5189/revpolarography.48.29 . eISSN 1884-7692 . ISSN 0034-6691 . Проверено 2 декабря 2021 г.

[Freedictionary-6] «Формальный потенциал» . TheFreeDictionary.com . Проверено 6 декабря 2021 г.

[PalmSens-7] Jump up to: ^а ^б ПалмСенс (2021). «Происхождение электрохимических потенциалов — PalmSens» . ПалмСенс . Проверено 6 декабря 2021 г.

[Brown_1949-8] Браун, Раймонд А.; Свифт, Эрнест Х. (1949). «Формальный потенциал сурьмяно-сурьмяной полуклетки в растворах соляной кислоты». Журнал Американского химического общества . 71 (8): 2719–2723. ISSN 0002-7863 . Цитата : Формальный потенциал определяется как потенциал полуэлемента, измеренный относительно стандартного водородного электрода, когда общая концентрация каждой степени окисления равна одной формальной.

[Harvey_2020-9] Харви, Дэвид (15 июня 2020 г.). «2.2: Концентрация» . Химия LibreTexts . Проверено 15 декабря 2021 г.

[Voet_2016-10] Воэт, Дональд; Воэт, Джудит Г.; Пратт, Шарлотта В. (2016). «Таблица 14-4. Стандартные потенциалы восстановления для некоторых полуреакций биохимического импорта» . Основы биохимии: жизнь на молекулярном уровне (5-е изд.). Уайли. п. 466. ИСБН 978-1-118-91840-1 .

[11] $р знак равно N А k$ ; см . газовую постоянную
$F знак равно N А е$ ; см . постоянную Фарадея

[Chem_Libre_Texts-12] «20.5: Энергия Гиббса и окислительно-восстановительные реакции» . Химия LibreTexts . 18 ноября 2014 г. Проверено 6 декабря 2021 г.

[13] Дж. Электроанал. хим. , 79 (1977), 259-266

[14] Караогланов, З. (январь 1906 г.), «О процессах окисления и восстановления при электролизе растворов солей железа» , Журнал электрохимии (на немецком языке), 12 (1): 5–16, doi : 10.1002/bbpc.19060120105

[15] Бард, Аллен Дж.; Инзельт, Дьёрдь; Шольц, Фриц, ред. (2012-10-02), «Уравнение Караогланова», Электрохимический словарь , Springer, стр. 527–528, ISBN 9783642295515

[16] Зутши, Камала (2008), Введение в полярографию и смежные методы , стр. 127–128, ISBN 9788122417913

[17] Журнал физической химии . Корнелльский университет. 1906.

[18] Хуйзенга, Джон Р. (1993). Холодный синтез: научное фиаско века (2-е изд.). Оксфорд и Нью-Йорк: Издательство Оксфордского университета. стр. 33, 47. ISBN. 978-0-19-855817-0 .

[Huot1989-19] Хуот, JY (1989). «Электролитическое гидрирование и аморфизация сплавов Pd-Zr». Журнал Электрохимического общества . 136 (3): 630–635. дои : 10.1149/1.2096700 . ISSN 0013-4651 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]