Принцип включения-исключения

Диаграмма Венна, показывающая объединение множеств A и B, поскольку все не в белом цвете

В комбинаторике , разделе математики , принцип включения-исключения — это метод подсчета, который обобщает известный метод получения количества элементов в объединении двух конечных множеств ; символически выражается как

$|A\cup B|=|A|+|B|-|A\cap B|$

где A и B — два конечных множества и | С | указывает мощность набора S (которую можно рассматривать как количество элементов набора, если набор конечен ). Формула выражает тот факт, что сумма размеров двух наборов может быть слишком большой, поскольку некоторые элементы могут быть посчитаны дважды. Элементы с двойным подсчетом — это те, которые находятся на пересечении двух наборов, и счет корректируется путем вычитания размера пересечения.

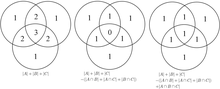
Принцип включения-исключения, являющийся обобщением случая двух множеств, возможно, более четко виден в случае трех множеств, который для множеств A , B и C определяется выражением

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$

Эту формулу можно проверить, подсчитав, сколько раз каждая область диаграммы Венна входит в правую часть формулы. В этом случае при удалении вкладов пересчитанных элементов количество элементов во взаимном пересечении трех наборов вычиталось слишком часто, поэтому его необходимо добавить обратно, чтобы получить правильную сумму.

Включение-исключение, проиллюстрированное диаграммой Венна для трех наборов

Обобщение результатов этих примеров дает принцип включения-исключения. Чтобы найти мощность объединения n множеств:

1. Включите мощности множеств.
2. Исключим мощности попарных пересечений.
3. Включите мощности тройных пересечений.
4. Исключите мощности четверных пересечений.
5. Включите мощности пятикратных пересечений.
6. Продолжайте до тех пор, пока мощность n -кортежного пересечения не будет включена (если n нечетно) или исключена ( n четно).

Название происходит от идеи, что принцип основан на чрезмерно щедром включении , за которым следует компенсирующее исключение .Эта концепция приписывается Аврааму де Муару (1718 г.), хотя впервые оно появляется в статье Даниэля да Силвы (1854 г.). а затем в статье Дж. Дж. Сильвестра (1883 г.). В связи с этими публикациями этот принцип иногда называют формулой Да Силвы или Сильвестра. Этот принцип можно рассматривать как пример метода сита, широко используемого в теории чисел и иногда называемого формулой сита .

Поскольку конечные вероятности вычисляются как отсчеты относительно мощности вероятностного пространства , формулы принципа включения-исключения остаются действительными, когда мощности множеств заменяются конечными вероятностями. В более общем плане обе версии принципа можно объединить под общим эгидой теории меры .

В очень абстрактной форме принцип включения-исключения можно выразить как вычисление обратной некоторой матрицы. Это обратное имеет особую структуру, что делает этот принцип чрезвычайно ценным методом в комбинаторике и смежных областях математики. Как Джан-Карло Рота : сказал

«Одним из наиболее полезных принципов перечисления в дискретной теории вероятностей и комбинаторной теории является знаменитый принцип включения-исключения. При умелом применении этот принцип позволил решить многие комбинаторные проблемы».

Формула

В своей общей формуле принцип включения-исключения утверждает, что для конечных множеств A ₁ , ..., An _{имеет место} тождество

$\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{i=1}^{n}|A_{i}|-\sum _{1\leqslant i<j\leqslant n}|A_{i}\cap A_{j}|+\sum _{1\leqslant i<j<k\leqslant n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n+1}\left|A_{1}\cap \cdots \cap A_{n}\right|.$ ( 1 )

Каждый член формулы включения-исключения постепенно корректирует подсчет, пока, наконец, каждая часть диаграммы Венна не будет подсчитана ровно один раз.

Это можно компактно записать как

$\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leqslant i_{1}<\cdots <i_{k}\leqslant n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)$

или

$\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{\emptyset \neq J\subseteq \{1,\ldots ,n\}}(-1)^{|J|+1}\left|\bigcap _{j\in J}A_{j}\right|.$

Другими словами, чтобы подсчитать количество элементов в конечном объединении конечных множеств, сначала просуммируйте мощности отдельных множеств, затем вычтите количество элементов, которые встречаются как минимум в двух множествах, а затем снова прибавьте количество элементов, которые появляются в не менее трех наборов, затем вычтите количество элементов, которые встречаются как минимум в четырех наборах, и так далее. Этот процесс всегда заканчивается, поскольку не может быть элементов, которые встречаются в большем количестве наборов в объединении. (Например, если $n=4,$ не может быть элементов, которые встречаются более чем $4$ наборы; эквивалентно, не может быть элементов, которые появляются хотя бы в $5$ наборы.)

В приложениях часто можно увидеть принцип, выраженный в дополнительной форме. То есть, если S — конечное универсальное множество , содержащее все A _i , и позволить ${\bar {A_{i}}}$ обозначим дополнение A _i в S , по законам Де Моргана имеем

$\left|\bigcap _{i=1}^{n}{\bar {A_{i}}}\right|=\left|S-\bigcup _{i=1}^{n}A_{i}\right|=|S|-\sum _{i=1}^{n}|A_{i}|+\sum _{1\leqslant i<j\leqslant n}|A_{i}\cap A_{j}|-\cdots +(-1)^{n}|A_{1}\cap \cdots \cap A_{n}|.$

В качестве другого варианта утверждения, пусть P ₁ , ..., P _n — список свойств, которыми могут обладать или не обладать элементы множества S , тогда принцип включения-исключения дает возможность вычислить количество элементов. из S , не обладающих ни одним из свойств. Просто пусть A _i будет подмножеством элементов S которые обладают свойством Pi _, и используют этот принцип в его дополнительной форме. Этот вариант принадлежит Джей Джей Сильвестру .

Обратите внимание, что если вы учтете только первые m<n сумм справа (в общей форме принципа), то вы получите завышенную оценку, если m нечетное, и заниженную, если m четное.

Примеры

Подсчет нарушений

Более сложный пример следующий.

Предположим, есть колода из n карт с номерами от 1 до n . Предположим, что карта с номером m находится в правильном положении, если это m. ^й карта в колоде. Сколькими способами W можно перетасовать карты так, чтобы хотя бы одна карта оказалась в правильном положении?

Начните с определения набора A _m , который представляет собой все упорядоченные карты с номером m. ^й карта правильная. Тогда количество заказов W , в которых хотя бы одна карта находится в правильной позиции m , равно

$W=\left|\bigcup _{m=1}^{n}A_{m}\right|.$

Применить принцип включения-исключения,

$W=\sum _{m_{1}=1}^{n}|A_{m_{1}}|-\sum _{1\leqslant m_{1}<m_{2}\leqslant n}|A_{m_{1}}\cap A_{m_{2}}|+\cdots +(-1)^{p-1}\sum _{1\leqslant m_{1}<\cdots <m_{p}\leqslant n}|A_{m_{1}}\cap \cdots \cap A_{m_{p}}|+\cdots$

Каждое значение $A_{m_{1}}\cap \cdots \cap A_{m_{p}}$ представляет собой набор тасовок, имеющих по меньшей мере p значений m ₁ , ..., m _p в правильном положении. Обратите внимание, что количество тасовок с правильными значениями хотя бы p зависит только от p , а не от конкретных значений $m$. Например, количество тасовок, имеющих цифру 1 ^ул. , 3 ^р-д , и 17 ^й карты в правильном положении равно количеству тасовок, в которых есть 2 ^nd , 5 ^й , и 13 ^й карточки в правильных положениях. Имеет значение только то, что из n карт 3 оказались в правильном положении. Таким образом, существуют ${\textstyle {n \choose p}}$ равные члены в p ^й суммирование (см. сочетание ).

$W={n \choose 1}|A_{1}|-{n \choose 2}|A_{1}\cap A_{2}|+\cdots +(-1)^{p-1}{n \choose p}|A_{1}\cap \cdots \cap A_{p}|+\cdots$

$|A_{1}\cap \cdots \cap A_{p}|$ — это количество упорядочений, в которых p элементов находятся в правильном положении, которое равно количеству способов упорядочить оставшиеся n — p элементов, или ( n — p )!. Таким образом, мы наконец получаем:

${\begin{aligned}W&={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+\cdots +(-1)^{p-1}{n \choose p}(n-p)!+\cdots \\&=\sum _{p=1}^{n}(-1)^{p-1}{n \choose p}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!(n-p)!}}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!}}\end{aligned}}$

Перестановка, при которой ни одна карта не находится в правильном положении, называется расстройством . Беру н ! Чтобы быть общим количеством перестановок, вероятность Q того, что случайное перетасовывание приведет к расстройству, определяется выражением

$Q=1-{\frac {W}{n!}}=\sum _{p=0}^{n}{\frac {(-1)^{p}}{p!}},$

усечение до n членов разложения Тейлора e + 1 ⁻¹ . Таким образом, вероятность угадать порядок перетасованной колоды карт и ошибиться в отношении каждой карты равна примерно e. ⁻¹ или 37%.

Особый случай

Ситуация, представленная в приведенном выше примере расстройства, возникает достаточно часто, чтобы заслуживать особого внимания. А именно, когда размеры множеств пересечений, фигурирующих в формулах принципа включения-исключения, зависят только от количества множеств в пересечениях, а не от того, какие множества появляются. Более формально, если пересечение

$A_{J}:=\bigcap _{j\in J}A_{j}$

имеет ту же мощность, скажем, α _k = | A _J |, для каждого k -элементного подмножества J из {1, ..., n }, то

$\left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.$

Или, в дополнительной форме, где универсальное множество S имеет мощность α ₀ ,

$\left|S\smallsetminus \bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\alpha _{k}.$

Обобщение формулы

Учитывая семейство (допускаются повторы) подмножеств A ₁ , A ₂ , ..., An _S универсального набора , принцип включения-исключения не вычисляет количество элементов S ни в одном из этих подмножеств. Обобщение этой концепции позволит вычислить количество элементов S , которые появляются ровно в некоторых фиксированных m из этих множеств.

Пусть N = [ n ] = {1,2,..., n }. Если мы определим $A_{\emptyset }=S$, то принцип включения-исключения можно записать как, используя обозначения предыдущего раздела; количество элементов S , содержащихся ни в одном из A _i, равно:

$\sum _{J\subseteq [n]}(-1)^{|J|}|A_{J}|.$

Если I — фиксированное подмножество набора индексов N , то количество элементов, принадлежащих A _i для всех i в I и ни для каких других значений, равно:

$\sum _{I\subseteq J}(-1)^{|J|-|I|}|A_{J}|.$

Определите наборы

$B_{k}=A_{I\cup \{k\}}{\text{ for }}k\in N\smallsetminus I.$

Ищем количество элементов ни в одном из , _Bk которые по принципу включения-исключения (с $B_{\emptyset }=A_{I}$), является

$\sum _{K\subseteq N\smallsetminus I}(-1)^{|K|}|B_{K}|.$

Соответствие K ↔ J = I ∪ K между подмножествами N \ I и подмножествами N , содержащими I, является биекцией, и если J и K соответствуют этому отображению, то B _K = A _J , что показывает, что результат верен.

По вероятности

По вероятности для событий A ₁ , ..., An _в вероятностном пространстве $(\Omega ,{\mathcal {F}},\mathbb {P} )$, принцип включения-исключения становится для n = 2

$\mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),$

для n = 3

$\mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})$

и вообще

$\mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{i=1}^{n}\mathbb {P} (A_{i})-\sum _{i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i<j<k}\mathbb {P} (A_{i}\cap A_{j}\cap A_{k})+\cdots +(-1)^{n-1}\sum _{i<...<n}\mathbb {P} \left(\bigcap _{i=1}^{n}A_{i}\right),$

которое можно записать в замкнутой форме как

$\mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{I\subseteq \{1,\ldots ,n\} \atop |I|=k}\mathbb {P} (A_{I})\right),$

где последняя сумма пробегает все подмножества I индексов 1, ..., n , содержащие ровно k элементов, и

$A_{I}:=\bigcap _{i\in I}A_{i}$

обозначает пересечение всех A _i с индексом в I .

Согласно неравенствам Бонферрони , сумма первых членов формулы поочередно является верхней и нижней границей для LHS . Это можно использовать в тех случаях, когда полная формула слишком громоздка.

Для общего пространства с мерой ( S ,Σ, µ ) и измеримых подмножеств A ₁ , ..., An _мера конечной меры приведенные выше тождества выполняются и тогда, когда вероятностная $\mathbb {P}$ заменяется мерой µ .

Особый случай

Если в вероятностной версии принципа включения-исключения вероятность пересечения A _I зависит только от мощности I , это означает, что для каждого k в {1, ..., n } существует a _k такой, что

$a_{k}=\mathbb {P} (A_{I}){\text{ for every }}I\subset \{1,\ldots ,n\}{\text{ with }}|I|=k,$

тогда приведенная выше формула упрощается до

$\mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}$

из-за комбинаторной интерпретации биномиального коэффициента ${\textstyle {\binom {n}{k}}}$. Например, если события $A_{i}$ независимы и одинаково распределены , то $\mathbb {P} (A_{i})=p$ для всех я и у нас есть $a_{k}=p^{k}$, и в этом случае приведенное выше выражение упрощается до

$\mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=1-(1-p)^{n}.$

(Этот результат можно получить и проще, рассмотрев пересечение дополнений событий $A_{i}$.)

Аналогичное упрощение возможно в случае общего пространства с мерой ( S , Σ, µ ) и измеримых подмножеств A ₁ , ..., An _{конечной} меры.

Другие формулы

Этот принцип иногда формулируется в форме это говорит о том, что если

$g(A)=\sum _{S\subseteq A}f(S)$

затем

$f(A)=\sum _{S\subseteq A}(-1)^{|A|-|S|}g(S)$ ( 2 )

Комбинаторная и вероятностная версии принципа включения-исключения являются примерами ( 2 ).

Доказательство

Брать ${\underline {m}}=\{1,2,\ldots ,m\}$, $f({\underline {m}})=0$, и

$f(S)=\left|\bigcap _{i\in {\underline {m}}\smallsetminus S}A_{i}\smallsetminus \bigcup _{i\in S}A_{i}\right|{\text{ and }}f(S)=\mathbb {P} \left(\bigcap _{i\in {\underline {m}}\smallsetminus S}A_{i}\smallsetminus \bigcup _{i\in S}A_{i}\right)$

соответственно для всех наборов $S$ с $S\subsetneq {\underline {m}}$. Тогда мы получаем

$g(A)=\left|\bigcap _{i\in {\underline {m}}\smallsetminus A}A_{i}\right|,\quad g({\underline {m}})=\left|\bigcup _{i\in {\underline {m}}}A_{i}\right|{\text{ and }}g(A)=\mathbb {P} \left(\bigcap _{i\in {\underline {m}}\smallsetminus A}A_{i}\right),~~g({\underline {m}})=\mathbb {P} \left(\bigcup _{i\in {\underline {m}}}A_{i}\right)$

соответственно для всех наборов $A$ с $A\subsetneq {\underline {m}}$. Это происходит потому, что элементы $a$ из $\cap _{i\in {\underline {m}}\smallsetminus A}A_{i}$ может содержаться в других $A_{i}$ ( $A_{i}$ с $i\in A$) а также, и $\cap \smallsetminus \cup$-формула проходит точно через все возможные расширения множеств $\{A_{i}\mid i\in {\underline {m}}\smallsetminus A\}$ с другими $A_{i}$, считая $a$ только для набора, который соответствует поведению членства $a$, если $S$ проходит через подмножества все $A$ (как в определении $g(A)$).

С $f({\underline {m}})=0$, получаем из ( 2 ) с $A={\underline {m}}$ что

$\sum _{{\underline {m}}\supseteq T\supsetneq \varnothing }(-1)^{|T|-1}g({\underline {m}}\smallsetminus T)=\sum _{\varnothing \subseteq S\subsetneq {\underline {m}}}(-1)^{m-|S|-1}g(S)=g({\underline {m}})$

и путем замены сторон следуют комбинаторная и вероятностная версии принципа включения-исключения.

Если человек видит число $n$ как набор его простых множителей, то ( 2 ) является обобщением формулы обращения Мёбиуса для без квадратов натуральных чисел . ( 2 ) рассматривается как формула обращения Мёбиуса для алгебры инцидентности частично упорядоченного множества всех подмножеств A. Следовательно ,

Для обобщения полной версии формулы обращения Мёбиуса ( 2 ) необходимо обобщить на мультимножества . Для мультимножеств вместо наборов ( 2 ) становится

$f(A)=\sum _{S\subseteq A}\mu (A-S)g(S)$ ( 3 )

где $A-S$ – это мультимножество, для которого $(A-S)\uplus S=A$, и

• µ ( S ) = 1, если S — множество (т.е. мультимножество без двойных элементов) четной мощности .
• µ ( S ) = −1, если S — множество (т. е. мультимножество без двойных элементов) нечетной мощности.
• µ ( S ) = 0, если S является собственным мультимножеством (т. е. S имеет двойные элементы).

Обратите внимание, что $\mu (A-S)$ это просто $(-1)^{|A|-|S|}$ из ( 2 ) в случае $A-S$ это набор.

Доказательство ( 3 )

Заменять $$g(S)=\sum _{T\subseteq S}f(T)$$в правой части ( 3 ). Обратите внимание, что $f(A)$ появляется один раз с обеих сторон ( 3 ). Поэтому мы должны показать, что для всех $T$ с $T\subsetneq A$, условия $f(T)$ сократите правую часть ( 3 ). Для этого возьмем фиксированное $T$ такой, что $T\subsetneq A$ и возьмем произвольное фиксированное $a\in A$ такой, что $a\notin T$.

Обратите внимание, что $A-S$ должен быть набор для каждого положительного или отрицательного проявления $f(T)$ в правой части ( 3 ), которое получается с помощью мультимножества $S$ такой, что $T\subseteq S\subseteq A$. Теперь каждое появление $f(T)$ в правой части ( 3 ), которое получается путем $S$ такой, что $A-S$ представляет собой набор, содержащий $a$ сокращается с тем, который получается путем соответствующего $S$ такой, что $A-S$ это множество, не содержащее $a$. Это дает желаемый результат.

Приложения

Принцип включения-исключения широко используется, и здесь можно упомянуть лишь некоторые из его применений.

Подсчет нарушений

Основная статья: Помешательство

Хорошо известное применение принципа включения-исключения относится к комбинаторной задаче подсчета всех нарушений конечного множества. Нарушением в себя , множества А называется биекция А . не имеющая неподвижных точек С помощью принципа включения-исключения можно показать, что если мощность A равна n , то количество нарушений равно [ n ! / e ] где [ x ] обозначает целое число ближайшее к x ; подробное доказательство доступно здесь , а также см. раздел примеров выше.

Впервые проблема подсчета количества нарушений встречается в одной из первых книг об азартных играх: « Эссе d'analyse sur les jeux de Risk» П.Р. де Монмора (1678–1719), которая была известна либо как «проблема Монмора», либо как «проблема Монмора». по названию, которое он дал ей, « проблема встреч ». Эта проблема также известна как проблема шляпной чеки.

Число нарушений также известно как субфакториал числа n , записываемый ! н . Отсюда следует, что если всем биекциям присвоена одинаковая вероятность, то вероятность того, что случайная биекция является нарушением, быстро приближается к 1/ e по мере роста n .

Подсчет пересечений

Принцип включения-исключения в сочетании с законом Де Моргана также можно использовать для подсчета мощности пересечения множеств. Позволять ${\overline {A_{k}}}$ представляют дополнение к относительно _Ak некоторого универсального множества A такого, что $A_{k}\subseteq A$ для каждого к . Тогда у нас есть

$\bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A_{i}}}}}$

тем самым превращая проблему поиска пересечения в проблему поиска объединения.

Раскраска графа

Принцип исключения включения лежит в основе алгоритмов для решения ряда NP-трудных задач разделения графов, таких как раскраска графов.

Хорошо известным применением этого принципа является построение хроматического полинома графа.

Совершенные паросочетания двудольного графа

Количество идеальных паросочетаний можно двудольного графа вычислить, используя этот принцип.

Количество on-функций

Учитывая конечные множества A и B , сколько сюръективных функций (онто-функций) существует из A в B ? Без ограничения общности мы можем взять A = {1, ..., k } и B = {1, ..., n }, поскольку значение имеют только мощности множеств. Используя S как набор всех функций от A до B и определяя для каждого i в B свойство Pi _как «функция пропускает элемент i в B » ( i не находится в образе функции), принцип включения-исключения дает количество онто-функций между A и B как:

$\sum _{j=0}^{n}{\binom {n}{j}}(-1)^{j}(n-j)^{k}.$

Перестановки с запрещенными позициями

Перестановка } , множества S = {1, ..., n в которой каждый элемент S ограничен тем, что он не находится в определенных позициях (здесь перестановка рассматривается как упорядочение элементов S ), называется перестановкой с запрещенными позиции . Например, при S = ​​{1,2,3,4} перестановки с ограничением, что элемент 1 не может находиться в позициях 1 или 3, а элемент 2 не может находиться в позиции 4, таковы: 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 и 4321. Полагая A _i набором позиций, в которых элементу i не разрешено находиться, а свойству P _i быть свойством, которое перестановка помещает элемент i в позицию в A _i , принцип включения-исключения можно использовать для подсчета количества перестановок, удовлетворяющих всем ограничениям.

В данном примере имеется 12 = 2(3!) перестановок со свойством P ₁ , 6 = 3! перестановки со свойством P ₂ и никакие перестановки не обладают свойствами P ₃ или P _4, поскольку для этих двух элементов нет ограничений. Таким образом, количество перестановок, удовлетворяющих ограничениям, равно:

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

Последняя цифра 4 в этом вычислении — это количество перестановок, имеющих оба свойства P ₁ и P ₂ . Других ненулевых вкладов в формулу нет.

Числа Стирлинга второго рода

Основная статья: Числа Стирлинга второго рода

Числа Стирлинга второго рода S ( n , k ) подсчитывают количество разбиений множества из n элементов на k непустые подмножества (неразличимые ящики ). Явную формулу для них можно получить, применив принцип включения-исключения к очень близкой задаче, а именно к подсчету числа разбиений n -множества на k непустых, но различимых ящиков ( упорядоченных непустых подмножеств). . Используя универсальное множество, состоящее из всех разбиений n -множества на k (возможно, пустых) различимых ящиков, A ₁ , A ₂ , ..., Ak _Pi и свойства , _, означающие, что в разбиении есть ящик A _i пустой, принцип включения-исключения дает ответ на соответствующий результат. Деление на к ! удаление искусственного упорядочения дает число Стирлинга второго рода:

$S(n,k)={\frac {1}{k!}}\sum _{t=0}^{k}(-1)^{t}{\binom {k}{t}}(k-t)^{n}.$

Ладейные полиномы

Основная статья: Полином Ладьи

Ладейный полином — это производящая функция количества способов разместить неатакующие ладьи на доске B , которая выглядит как подмножество клеток шахматной доски ; то есть никакие две ладьи не могут находиться в одной строке или столбце. Доска B — это любое подмножество квадратов прямоугольной доски с n строками и m столбцами; мы думаем об этом как о полях, на которые можно поставить ладью. Коэффициент B , r _k ( ) при x ^к в ладейном полиноме R _B ( x ) — это количество способов , которыми k ладей, ни одна из которых не атакует другую, можно расположить в клетках B . Для любой доски B существует дополнительная доска. $B'$ состоящая из клеток прямоугольной доски, которых нет в B . Эта дополнительная доска также имеет ладейный полином. $R_{B'}(x)$ с коэффициентами $r_{k}(B').$

Иногда бывает удобно вычислить старший коэффициент ладейного полинома через коэффициенты ладейного полинома дополнительной доски. Без ограничения общности можно считать, что n ≤ m , поэтому этот коэффициент равен r _n ( B ). Число способов разместить n неатакующих ладей на полной «шахматной доске» размера n × m (без учета того, размещены ли ладьи в клетках доски B ) определяется падающим факториалом :

$(m)_{n}=m(m-1)(m-2)\cdots (m-n+1).$

Полагая P _i свойством, согласно которому при назначении n неатакующих ладей на всей доске есть ладья в столбце i , которая не находится в поле доски B , тогда по принципу включения-исключения мы имеем:

$r_{n}(B)=\sum _{t=0}^{n}(-1)^{t}(m-t)_{n-t}r_{t}(B').$

Фи-функция Эйлера

Основная статья: функция Эйлера totient

Тотент или фи-функция Эйлера, φ ( n ) — это арифметическая функция , которая подсчитывает количество натуральных чисел, меньших или равных n , которые являются относительно простыми с n . То есть, если n — целое положительное число , то φ( n ) — это количество целых чисел k в диапазоне 1 ≤ k ≤ n, которые не имеют общего множителя с n, кроме 1. Для получения используется принцип включения-исключения. формула для φ( n ). Пусть S будет набором {1, ..., n } и определим свойство P _i, заключающееся в том, что число в S делится на простое число p _i , для 1 ⩽ i ⩽ r , где факторизация простая

$n=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{r}^{a_{r}}.$

Затем,

$\varphi (n)=n-\sum _{i=1}^{r}{\frac {n}{p_{i}}}+\sum _{1\leqslant i<j\leqslant r}{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i}}}\right).$

Метод гиперболы Дирихле

Основная статья: Метод гиперболы Дирихле

Пример метода гиперболы Дирихле с $n=10,$ $a\approx 2.7,$ и $b\approx 3.7.$

Метод гиперболы Дирихле повторно выражает сумму мультипликативной функции. $f(n)$ выбрав подходящую свертку Дирихле $f=g\ast h$, учитывая, что сумма

$F(n)=\sum _{k=1}^{n}f(k)=\sum _{k=1}^{n}\sum _{xy=k}^{}g(x)h(y)$

можно представить как сумму по узлам решетки в области, ограниченной $x\geq 1$, $y\geq 1$, и $xy\leq n$, разделив эту область на две перекрывающиеся субрегионы и, наконец, используя принцип включения-исключения, чтобы сделать вывод, что

$F(n)=\sum _{k=1}^{n}f(k)=\sum _{k=1}^{n}\sum _{xy=k}^{}g(x)h(y)=\sum _{x=1}^{a}\sum _{y=1}^{n/x}g(x)h(y)+\sum _{y=1}^{b}\sum _{x=1}^{n/y}g(x)h(y)-\sum _{x=1}^{a}\sum _{y=1}^{b}g(x)h(y).$

Принцип разбавленного включения-исключения

См. Также: неравенства Бонферрони.

Во многих случаях, когда принцип мог бы дать точную формулу (в частности, при подсчете простых чисел с помощью решета Эратосфена ), возникающая формула не несет полезного содержания, поскольку число членов в ней избыточно. Если каждый термин по отдельности можно точно оценить, накопление ошибок может означать, что формула включения-исключения не применима напрямую. В теории чисел эту трудность рассмотрел Вигго Брун . После медленного старта его идеи были подхвачены другими, и было разработано большое разнообразие ситовых методов . Например, они могут попытаться найти верхние границы для «просеянных» множеств, а не точную формулу.

Пусть A ₁ , ..., An _— произвольные множества и p ₁ , ..., p _n действительные числа в единичном интервале [0, 1] . Тогда для каждого четного числа k из {0, ..., n } индикаторные функции удовлетворяют неравенству:

$1_{A_{1}\cup \cdots \cup A_{n}}\geq \sum _{j=1}^{k}(-1)^{j-1}\sum _{1\leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.$

Доказательство основного утверждения

Выберем элемент, входящий в объединение всех множеств, и пусть $A_{1},A_{2},\dots ,A_{t}$ быть отдельными наборами, содержащими его. (Обратите внимание, что t > 0.) Поскольку элемент учитывается ровно один раз в левой части уравнения ( 1 ), нам нужно показать, что он учитывается ровно один раз в правой части. В правой части единственные ненулевые вклады возникают, когда все подмножества в конкретном терме содержат выбранный элемент, то есть все подмножества выбираются из $A_{1},A_{2},\dots ,A_{t}$. Вклад равен одному для каждого из этих наборов (плюс или минус в зависимости от термина) и, следовательно, представляет собой просто (со знаком) количество этих подмножеств, используемых в термине. Тогда у нас есть:

${\begin{aligned}|\{A_{i}\mid 1\leqslant i\leqslant t\}|&-|\{A_{i}\cap A_{j}\mid 1\leqslant i<j\leqslant t\}|+\cdots +(-1)^{t+1}|\{A_{1}\cap A_{2}\cap \cdots \cap A_{t}\}|={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}}.\end{aligned}}$

По теореме биномиальной

$0=(1-1)^{t}={\binom {t}{0}}-{\binom {t}{1}}+{\binom {t}{2}}-\cdots +(-1)^{t}{\binom {t}{t}}.$

Используя тот факт, что ${\binom {t}{0}}=1$ и переставив термины, мы имеем

$1={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}},$

и поэтому выбранный элемент учитывается только один раз в правой части уравнения ( 1 ).

Алгебраическое доказательство

Алгебраическое доказательство можно получить с помощью индикаторных функций (также известных как характеристические функции). Индикаторной функцией подмножества S множества X является функция

${\begin{aligned}&\mathbf {1} _{S}:X\to \{0,1\}\\&\mathbf {1} _{S}(x)={\begin{cases}1&x\in S\\0&x\notin S\end{cases}}\end{aligned}}$

Если $A$ и $B$ представляют собой два подмножества $X$, затем

$\mathbf {1} _{A}\cdot \mathbf {1} _{B}=\mathbf {1} _{A\cap B}.$

Пусть A обозначает объединение ${\textstyle \bigcup _{i=1}^{n}A_{i}}$ множеств A ₁ , ... An _, . Чтобы доказать принцип включения-исключения в общем виде, сначала проверим тождество

$\mathbf {1} _{A}=\sum _{k=1}^{n}(-1)^{k-1}\sum _{I\subset \{1,\ldots ,n\} \atop |I|=k}\mathbf {1} _{A_{I}}$ ( 4 )

для индикаторных функций, где:

$A_{I}=\bigcap _{i\in I}A_{i}.$

Следующая функция

$\left(\mathbf {1} _{A}-\mathbf {1} _{A_{1}}\right)\left(\mathbf {1} _{A}-\mathbf {1} _{A_{2}}\right)\cdots \left(\mathbf {1} _{A}-\mathbf {1} _{A_{n}}\right)=0,$

тождественно равен нулю, потому что: если x не находится в A , то все факторы равны 0−0 = 0; в противном случае, если x принадлежит некоторому Am _{действительно} , то соответствующее m ^й коэффициент равен 1−1=0. Если разложить произведение в левой части, получится уравнение ( 4 ).

Чтобы доказать принцип включения-исключения мощности множеств, просуммируйте уравнение ( 4 всем x в объединении A ₁ , ..., An _. ) по Чтобы получить версию, используемую в теории вероятности, возьмите математическое ожидание в ( 4 ). В общем, проинтегрируйте уравнение ( 4 ) по µ . Всегда используйте линейность в этих выводах.

См. также

• Неравенство Буля - неравенство, применимое к вероятностным пространствам
• Комбинаторные принципы - Методы, используемые в комбинаторике.
• Идентичность максимума и минимума - связывает максимальный элемент набора чисел и минимумы его непустых подмножеств.
• Проблема с ожерельем
• Принцип ячейки : если предметов больше, чем коробок с ними, одна коробка должна содержать как минимум два предмета.
• Формула Шютта – Несбитта - математическая формула в теории вероятностей. Страницы, отображающие описания викиданных в качестве запасного варианта.

Ссылки

• Алленби, RBJT; Сломсон, Алан (2010), Как считать: введение в комбинаторику , дискретную математику и ее приложения (2-е изд.), CRC Press, стр. 51–60, ISBN  9781420082609
• Бьёрклунд, А.; Хусфельдт, Т.; Койвисто, М. (2009), «Разбиение наборов посредством включения-исключения», SIAM Journal on Computing , 39 (2): 546–563, CiteSeerX   10.1.1.526.9573 , doi : 10.1137/070683933
• Бруальди, Ричард А. (2010), Вводная комбинаторика (5-е изд.), Прентис-Холл, ISBN  9780136020400
• Кэмерон, Питер Дж. (1994), Комбинаторика: темы, методы, алгоритмы , издательство Кембриджского университета, ISBN  0-521-45761-0
• Фернандес, Роберто; Счастлив, Юрг ; Алан Д., Сокал (1992), Случайные блуждания, критические явления и тривиальность в квантовой теории поля , Тексты и монографии по физике, Берлин: Springer-Verlag , стр. xviii+444, ISBN  3-540-54358-9 , МР   1219313 , Збл   0761.60061
• Грэм, РЛ; Гретшель, М .; Ловас, Л. (1995), Справочник по комбинаторике (том 2) , MIT Press – North Holland, ISBN  9780262071710
• Гросс, Джонатан Л. (2008), Комбинаторные методы с компьютерными приложениями , Chapman&Hall/CRC, ISBN  9781584887430
• «Принцип включения и исключения» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Мазур, Дэвид Р. (2010), Экскурсия по комбинаторике , Математическая ассоциация Америки, ISBN  9780883857625
• Робертс, Фред С.; Тесман, Барри (2009), Прикладная комбинаторика (2-е изд.), CRC Press, ISBN  9781420099829
• Стэнли, Ричард П. (1986), Том I перечислительной комбинаторики , Wadsworth & Brooks/Cole, ISBN  0534065465
• ван Линт, Дж. Х.; Уилсон, Р.М. (1992), Курс комбинаторики , издательство Кембриджского университета, ISBN  0521422604

Эта статья включает в себя материал, основанный на принципе включения-исключения в PlanetMath , который распространяется по лицензии Creative Commons Attribution/Share-Alike License .