Экзистенциальный граф
Вы можете помочь дополнить эту статью текстом, переведенным из соответствующей статьи на немецком языке . (Май 2017 г.) Нажмите [показать], чтобы просмотреть важные инструкции по переводу. |
| Часть серии о |
| Чарльз Сандерс Пирс |
|---|
 |
| Прагматизм в эпистемологии |
| Логика |
| Семиотическая теория |
| Разные взносы |
| Биографический |
Экзистенциальный граф — это тип схематического или визуального обозначения логических выражений, предложенный Чарльзом Сандерсом Пирсом , который писал о графической логике еще в 1882 году. [1] и продолжал развивать этот метод до своей смерти в 1914 году.
Графики [ править ]
Пирс предложил три системы экзистенциальных графов:
- альфа , изоморфная и логике предложений двухэлементной булевой алгебре ;
- beta , изоморфная логике первого порядка с единицей, со всеми закрытыми формулами;
- гамма , (почти) изоморфная нормальной модальной логике .
Альфа гнездится в бета и гамма . Бета не вложена в гамма , квантифицированная модальная логика более общая, чем предложенная Пирсом.
Альфа [ править ]
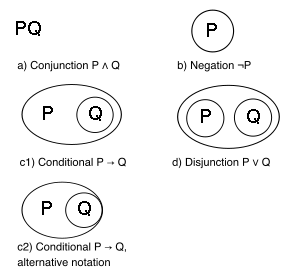
Синтаксис :
- Пустая страница;
- Отдельные буквы или фразы, написанные в любом месте страницы;
- Любой граф может быть заключен в простую замкнутую кривую, называемую разрезом или sep . Разрез может быть пустым. Разрезы могут вкладываться и объединяться по желанию, но никогда не должны пересекаться.
Любая правильно сформированная часть графа является подграфом .
Семантика такова :
- Пустая страница означает Истину ;
- Буквы, фразы, подграфы и целые графики могут быть истинными или ложными ;
- Охват подграфа разрезом эквивалентен логическому отрицанию или логическому дополнению . Следовательно, пустой разрез обозначает False ;
- Все подграфы внутри данного разреза молчаливо соединены .
Следовательно, альфа- графики представляют собой минималистскую систему обозначений логики предложений , основанную на выразительной адекватности «И» и « Не» . Альфа - графы представляют собой радикальное упрощение двухэлементной булевой алгебры и функторов истинности .
Глубина . объекта — это количество разрезов, которые его окружают
Правила вывода :
- Вставка. Любой подграф может быть вставлен в глубину с нечетным номером.
- Стирание. Любой подграф четной глубины может быть удален.
Правила эквивалентности :
- Двойной разрез. Вокруг любого подграфа можно провести пару разрезов, между которыми нет ничего. Аналогичным образом можно стереть два вложенных друг в друга выреза, между которыми ничего нет. Это правило эквивалентно булевой инволюции.
- Итерация/деитерация. Чтобы понять это правило, лучше всего рассматривать граф как древовидную структуру, имеющую узлы и предков . Любой подграф P в узле n может быть скопирован в любой узел в зависимости от n . Аналогично, любой подграф P в узле n может быть стерт, если существует копия P в некотором узле, являющемся предком n (т. е. в некотором узле, от которого зависит n ). Эквивалентное правило в алгебраическом контексте см. в C2 в разделе «Законы формы» .
Доказательство манипулирует графиком с помощью ряда шагов, каждый из которых оправдывается одним из приведенных выше правил. Если граф можно пошагово свести к пустой странице или пустому разрезу, это то, что сейчас называют тавтологией ( или ее дополнением, противоречием). Графы, которые нельзя упростить до определенной точки, являются аналогами выполнимых формул логики первого порядка .
Бета [ править ]
Пирс записывал предикаты, используя интуитивно понятные английские фразы; также можно использовать стандартные обозначения современной логики — заглавные латинские буквы. Точка утверждает существование некоторого индивидуума в сфере дискурса . Несколько экземпляров одного и того же объекта связаны линией, называемой «линией идентичности». не существует буквальных переменных или кванторов В смысле логики первого порядка . Линия идентичности, соединяющая два или более предикатов, может быть прочитана как утверждение, что предикаты имеют общую переменную. Наличие линий идентичности требует изменения альфа- правил эквивалентности.
Бета-графики можно рассматривать как систему, в которой все формулы следует рассматривать как замкнутые, поскольку все переменные имеют неявную количественную оценку. Если «самая мелкая» часть линии идентичности имеет четную (нечетную) глубину, соответствующая переменная неявно определяется экзистенциально ( универсально ).
Земан (1964) был первым, кто заметил, что бета- графы изоморфны логике первого порядка с равенством (см. также Земан 1967). Однако вторичная литература, особенно Робертс (1973) и Шин (2002), не пришли к единому мнению относительно того, почему это так. Работы Пирса не затрагивают этот вопрос, поскольку логика первого порядка была впервые четко сформулирована всего через несколько лет после его смерти, в первом издании 1928 года « Дэвида Гильберта и Вильгельма Аккермана Принципов математической логики» .
Гамма [ править ]
Добавьте к синтаксису альфа второй вид простой замкнутой кривой , написанной с использованием пунктирной, а не сплошной линии. Пирс предложил правила для этого второго типа разреза, который можно рассматривать как примитивный унарный оператор модальной логики .
Земан (1964) был первым, кто заметил, что простые поправки к правилам гамма -графа приводят к хорошо известным модальным логикам S4 и S5 . Следовательно, гамма- графики можно рассматривать как своеобразную форму нормальной модальной логики . Эта находка Земана по сей день осталась незамеченной, но, тем не менее, включена сюда как представляющий интерес.
Роль Пирса [ править ]
Экзистенциальные графы являются любопытным детищем Пирса логика / математика и основателя основного направления семиотики . Графическая логика Пирса — лишь одно из многих его достижений в области логики и математики. В серии статей, начавшихся в 1867 году и завершившихся его классической статьей в Американском журнале математики 1885 года , Пирс разработал большую часть двухэлементной булевой алгебры , исчисления высказываний , квантификации и исчисления предикатов , а также некоторые элементарные теории множеств . Теоретики моделей считают Пирса первым в своем роде. Он также расширил Де Моргана алгебру отношений . Он остановился на металогике (которая ускользнула даже от Principia Mathematica ).
теория Пирса Но развивающаяся семиотическая заставила его усомниться в ценности логики, сформулированной с использованием традиционных линейных обозначений, и предпочесть, чтобы логика и математика записывались в двух (или даже трех) измерениях. Его работа вышла за рамки диаграмм Эйлера и Венна в 1880 году их редакции . В книге Фреге 1879 года «Begriffsschrift» также использовалась двумерная система обозначений логики, но она сильно отличалась от обозначения Пирса.
В первой опубликованной статье Пирса по графической логике (перепечатанной в третьем томе его « Сборника статей ») была предложена система, двойственная (по сути) альфа - экзистенциальным графам, называемая энтитативными графами . Он очень скоро отказался от этого формализма в пользу экзистенциальных графов. В 1911 году Виктория леди Уэлби показала экзистенциальные графики К. К. Огдену , который посчитал, что их можно с пользой объединить с мыслями Уэлби в «менее заумной форме». [2] В остальном они не привлекали особого внимания при его жизни и неизменно подвергались клевете или игнорированию после его смерти, вплоть до защиты докторских диссертаций Робертсом (1964) и Земаном (1964).
См. также [ править ]
Ссылки [ править ]
- ^ Пирс, CS, «[О узлах и переломах в логике]» (название редактора MS 427 (новая система нумерации), осень – зима 1882 г.) и «Письмо Пирса О.Г. Митчеллу» (L 294, 21 декабря 1882), Сочинения Чарльза С. Пирса , т. 4, «Соединения» на стр. 391–393 ( предварительный просмотр Google ) и письмо на стр. 394–399 ( предварительный просмотр Google ). См. Сова, Джон Ф. (1997), «Сопоставление логической структуры с лингвистической структурой», Исследования по логике Чарльза Сандерса Пирса , Натана Хаузера, Дона Д. Робертса и Джеймса Ван Эвра, редакторов, Блумингтон и Индианаполис: Издательство Индиана Университета. , стр. 418–444, см. 420, 425, 426, 428.
- ^ Петрилли, Сьюзен (2017). Виктория Уэлби и наука о знаках: значения, семиотика, философия языка . Рутледж. ISBN 978-1-351-29598-7 .
Дальнейшее чтение [ править ]
Основная литература [ править ]
- 1931–1935 и 1958. Сборник статей Чарльза Сандерса Пирса . Том 4, Книга II: «Экзистенциальные графы», состоит из параграфов 347–584. Обсуждение также начинается в пункте 617.
- Параграфы 347–349 (II.1.1. «Логическая диаграмма») - определение Пирса «Логическая диаграмма (или график)» в Болдуина Словаре философии и психологии (1902), т. 2, с. 28 . Классика по истории психологии Епринт .
- Параграфы 350–371 (II.1.2. «О диаграммах Эйлера») — из «Графиков» (рукопись 479) в. 1903.
- Пункты 372–584 Эпринт .
- Параграфы 372–393 (II.2. «Символическая логика») - часть «Символической логики» Пирса в Словаре философии и психологии Болдуина (1902) , т. 2, стр. 645–650 , начиная (около верха второго столбца) с «Если определить символическую логику...». Параграф 393 (DPP2 Болдуина, стр. 650) написан Пирсом и Кристиной Лэдд-Франклин («CSP, CLF»).
- Параграфы 394–417 (II.3. «Экзистенциальные графы») — из брошюры Пирса «Программа по некоторым темам логики» , стр. 15–23, Alfred Mudge & Son, Бостон (1903).
- Параграфы 418–509 (II.4. «Об экзистенциальных графах, диаграммах Эйлера и логической алгебре») — из «Логических трактатов, № 2» (рукопись 492), ок. 1903.
- Параграфы 510–529 (II.5. «Гамма-часть экзистенциальных графов») — из «Лекций Лоуэлла 1903 года», лекция IV (рукопись 467).
- Параграфы 530–572 (II.6) — «Пролегомены к апологии прагматизма» (1906), «Монист» , т. XVI, н. 4, стр. 492-546 . Исправления (1907 г.) в «Монисте против XVII», с. 160 .
- Параграфы 573–584 (II.7. «Улучшение гамма-графов») - из «Для Национальной академии наук, апрельское собрание 1906 года в Вашингтоне» (рукопись 490).
- Параграфы 617–623 (по крайней мере) (в книге III, гл. 2, § 2, абзацы 594–642) — из «Некоторые удивительные лабиринты: объяснение любопытства первого», The Monist , т. XVIII, 1908, н. 3, стр. 416-464 , см. начальные стр. 440 .
- 1992. «Лекция третья: Логика родственников», Рассуждение и логика вещей , стр. 146–164. Кетнер, Кеннет Лейн (редактирование и введение) и Хилари Патнэм (комментарии). Издательство Гарвардского университета . Лекции Пирса 1898 года в Кембридже, Массачусетс.
- 1977, 2001. Семиотика и значение : переписка между К.С. Пирсом и Викторией Леди Уэлби . Хардвик, CS, изд. Лаббок, Техас: Издательство Техасского технологического университета. 2-е издание 2001 г.
- Транскрипция MS 514 Пирса (1909 г.), отредактированная с комментариями Джона Совы .
В настоящее время хронологическое критическое издание работ Пирса «Сочинения » распространяется только на 1892 год. Большая часть работ Пирса по логическим графам состоит из рукописей, написанных после этой даты и до сих пор не опубликованных. Следовательно, наше понимание графической логики Пирса, вероятно, изменится по мере появления остальных 23 томов хронологического издания.
Вторичная литература [ править ]
- Хаммер, Эрик М. (1998), «Семантика экзистенциальных графов», Journal of Philosophical Logic 27 : 489–503.
- Кетнер, Кеннет Лейн
- (1981), «Лучший пример семиозиса и его использования в преподавании семиотики», Американский журнал семиотики , т. I, n. 1–2, стр. 47–83. Статья представляет собой введение в экзистенциальные графы.
- (1990), «Элементы логики: введение в экзистенциальные графики Пирса» , издательство Техасского технологического университета, Лаббок, Техас, 99 страниц, в спиральном переплете.
- Кейруш, Жоао и Стьернфельт, Фредерик
- (2011), «Диаграмматическое рассуждение и логическое представление Пирса», Semiotica vol. 186 (1/4). (Специальный выпуск диаграммной логики Пирса.) [1]
- Робертс, Дон Д.
- (1964), «Экзистенциальные графики и естественная дедукция» в Муре, ЕС, и Робине, Р.С., ред., Исследования по философии К.С. Пирса, 2-я серия . Амхерст, Массачусетс: Издательство Массачусетского университета . Первая публикация, демонстрирующая сочувствие и понимание графической логики Пирса.
- (1973). Экзистенциальные графы К.С. Пирса. Джон Бенджаминс. Результат его диссертации 1963 года.
- Шин, Сун-Джу (2002), Знаковая логика графиков Пирса . МТИ Пресс.
- Саламеа, Фернандо . Логика непрерывности Пирса. Доцент Пресс, Бостон, Массачусетс. 2012. ISBN 9 780983 700494.
- Часть II: Экзистенциальные графики Пирса, стр. 76–162.
- Земан, Джей Джей
- (1964), Графическая логика К.С. Пирса. Архивировано 14 сентября 2018 г. в Wayback Machine. Неопубликованный доктор философии. диссертацию подал в Чикагский университет .
- (1967), «Система неявной количественной оценки», Журнал символической логики 32 : 480–504.
Внешние ссылки [ править ]
- Стэнфордская энциклопедия философии : логика Пирса и Сун-Джу Шина Эрика Хаммера.
- Дау, Фритьоф, Экзистенциальные графики Пирса --- Литература и ссылки. Аннотированная библиография по экзистенциальным графам.
- Готшалл, Кристиан, Proof Builder. Архивировано 12 февраля 2006 г. в Wayback Machine — Java-апплет для построения альфа-графиков.
- Лю, Синь-Вэнь, « Литература по экзистенциальным графам К.С. Пирса » (через Wayback Machine), Институт философии Китайской академии социальных наук, Пекин, КНР.
- Сова, Джон Ф. «Законы, факты и контексты: основы мультимодального рассуждения» . Проверено 23 октября 2009 г. (Примечание. Экзистенциальные графы и концептуальные графы .)
- Ван Хёвельн, Брэм, « Экзистенциальные графы. Архивировано 29 августа 2009 г. в Wayback Machine », кафедра когнитивных наук, Политехнический институт Ренсселера . Только Альфа.
- Земан, Джей Дж., « Экзистенциальные графы ». С четырьмя онлайн-статьями Пирса.