Количественная генетика

Количественная генетика — это изучение количественных признаков , которые представляют собой фенотипы , которые постоянно изменяются (например, рост или масса), в отличие от фенотипов и генных продуктов, которые можно идентифицировать дискретно , таких как цвет глаз или наличие определенного биохимического вещества.

Обе эти ветви генетики используют частоты различных аллелей гена для анализа закономерностей наследования между в размножающихся популяциях (гамодемах) и объединяют их с концепциями простого менделевского наследования поколениями и потомками. В то время как популяционная генетика может сосредоточиться на конкретных генах и продуктах их последующего метаболизма, количественная генетика больше фокусируется на внешних фенотипах и дает лишь обобщение лежащей в их основе генетики.

Из-за непрерывного распределения фенотипических значений количественная генетика должна использовать множество других статистических методов (таких как размер эффекта , среднее значение и дисперсия ), чтобы связать фенотипы (атрибуты) с генотипами. Некоторые фенотипы можно анализировать либо как дискретные категории, либо как непрерывные фенотипы, в зависимости от определения пороговых значений или метрики, используемой для их количественной оценки. Сам Мендель должен был обсудить этот вопрос в своей знаменитой статье: особенно в отношении атрибута его гороха высокий/карликовый , который на самом деле был получен путем добавления точки отсечения к «длине стебля». Анализ локусов количественных признаков или QTL, является более поздним дополнением к количественной генетике, более непосредственно связывающим ее с молекулярной генетикой .

Генные эффекты

У диплоидных организмов средняя генотипическая «ценность» (значение локуса) может определяться «эффектом» аллеля вместе с эффектом доминирования , а также тем, как гены взаимодействуют с генами в других локусах ( эпистаз ). Основатель количественной генетики сэр Рональд Фишер многое из этого осознал, когда предложил первую математику в этой области генетики.

Генные эффекты и значения фенотипа.

Будучи статистиком, он определил эффекты генов как отклонения от центрального значения, что позволило использовать такие статистические понятия, как среднее значение и дисперсия, которые используют эту идею. Центральным значением, которое он выбрал для гена, была середина между двумя противоположными гомозиготами в одном локусе. Отклонение оттуда к «большому» гомозиготному генотипу можно назвать « +а »; и, следовательно, это « -а » от той же средней точки до «меньшего» гомозиготного генотипа. Это упомянутый выше эффект «аллеля». Отклонение гетерозигот от одной и той же средней точки можно назвать « d », это и есть упомянутый выше эффект «доминирования». Схема отражает идею. Однако на самом деле мы измеряем фенотипы, и на рисунке также показано, как наблюдаемые фенотипы связаны с эффектами генов. Формальные определения этих эффектов признают этот фенотипический фокус. Статистически эпистаз рассматривается как взаимодействие (т. е. несоответствие), но эпигенетика предполагает, что может потребоваться новый подход.

Если 0 < d < a , доминирование считается частичным или неполным , тогда как d = a указывает на полное или классическое доминирование. Раньше d > a было известно как «чрезмерное доминирование».

Атрибут гороха Менделя «длина стебля» дает нам хороший пример. Мендель заявил, что длина стебля высоких чистокровных родителей колебалась от 6–7 футов (183–213 см), что дает средний рост 198 см (= P1). Короткие родители имели длину стебля от 0,75 до 1,25 фута (23–46 см) с округлой медианой 34 см (= P2). Их гибрид имел длину от 6–7,5 футов (183–229 см) со средней длиной 206 см (= F1). Среднее значение P1 и P2 составляет 116 см, что является фенотипическим значением средней точки гомозигот (mp). Аллельный эффект ( а ) составляет [P1-mp] = 82 см = -[P2-mp]. Эффект доминирования ( d ) составляет [F1-mp] = 90 см. Этот исторический пример ясно иллюстрирует, как связаны значения фенотипа и эффекты генов.

Частоты аллелей и генотипов

Для получения средних значений, дисперсий и других статистических данных как количества , так и их появление необходимы . Эффекты генов (выше) обеспечивают основу для количественных показателей , а частоты контрастирующих аллелей в пуле гамет оплодотворения предоставляют информацию о явлениях .

Анализ полового размножения.

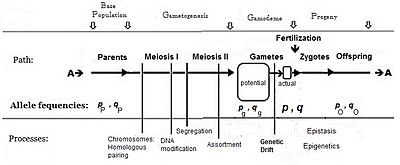
Обычно частота аллеля, вызывающая «большее» фенотипа (включая доминирование), обозначается символом p , а частота контрастного аллеля — q . Первоначальное предположение, сделанное при создании алгебры, заключалось в том, что родительская популяция была бесконечной и имела случайное спаривание, что было сделано просто для облегчения вывода. Последующие математические разработки также показали, что распределение частот внутри эффективного пула гамет было однородным: не было локальных возмущений при изменении p и q . Глядя на диаграммный анализ полового размножения, это то же самое, что заявить, что p _P = p _g = p ; и аналогично для q . Эта система спаривания, основанная на этих предположениях, стала известна как «панмиксия».

Панмиксия редко встречается в природе. поскольку распространение гамет может быть ограничено, например, ограничениями на распространение, поведением или случайным отбором проб (эти локальные возмущения, упомянутые выше). Хорошо известно, что в природе происходит огромная потеря гамет, поэтому на диаграмме потенциальный пул гамет изображен отдельно от реального пула гамет. Только последний устанавливает определённые частоты для зигот: это и есть истинная «гамодема» («гамо» относится к гаметам, а «дема» происходит от греческого слова «популяция»). Но, согласно предположениям Фишера, гамодема может быть эффективно расширена обратно до потенциального пула гамет и даже обратно до родительской базовой популяции («исходной» популяции). Случайная выборка, возникающая, когда небольшие «действительные» пулы гамет отбираются из большого «потенциального» пула гамет, известна как генетический дрейф и рассматривается далее.

Хотя панмиксия, возможно, не широко распространена, вероятность ее возникновения все же имеет место, хотя она может быть лишь эфемерной из-за этих локальных нарушений. Было показано, например, что F2, полученный в результате случайного оплодотворения особей F1 ( аллогамный F2) после гибридизации, является источником новой потенциально панмиктической популяции. Также было показано, что если бы панмиктическое случайное оплодотворение происходило постоянно, оно сохраняло бы одни и те же частоты аллелей и генотипов в каждом последующем панмиктическом половом поколении — это и есть равновесие Харди Вайнберга . Однако как только генетический дрейф был инициирован локальной случайной выборкой гамет, равновесие нарушилось.

Случайное оплодотворение

Считается, что мужские и женские гаметы в реальном оплодотворяющем пуле обычно имеют одинаковые частоты соответствующих аллелей. (Учитываются исключения.) Это означает, что когда p мужских гамет, несущих аллель А , случайным образом оплодотворяют p женских гамет, несущих тот же аллель, полученная зигота имеет генотип АА , и при случайном оплодотворении сочетание происходит с частотой p x р (= р ² ). Аналогично зигота аа возникает с частотой q ² . Гетерозиготы ( Аа ) могут возникнуть двумя способами: когда p самец ( аллель А ) случайным образом оплодотворяет q женские ( аллель а ) гаметы, и наоборот . Таким образом, результирующая частота гетерозиготных зигот равна 2pq . Обратите внимание, что такая популяция никогда не бывает гетерозиготной более чем наполовину, причем этот максимум наблюдается при p = q = 0,5.

Таким образом, при случайном оплодотворении частоты зигот (генотипов) представляют собой квадратичное расширение гаметических (аллельных) частот: ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$. (Знак «=1» означает, что частоты указаны в дробях, а не в процентах; и что в предлагаемой структуре нет пропусков.)

Обратите внимание, что «случайное оплодотворение» и «панмиксия» не являются синонимами.

Исследовательский крест Менделя – контраст

Эксперименты Менделя с горошком были построены путем установления чистокровных родителей с «противоположными» фенотипами по каждому признаку. Это означало, что каждый противоположный родитель был гомозиготен только по соответствующему аллелю. В нашем примере «высокий против карлика» высокий родитель будет иметь генотип TT с p = 1 (и q = 0 ); в то время как родитель-карлик будет иметь генотип tt с q = 1 (и p = 0 ). После контролируемого скрещивания их гибридом является Tt с p = q = ⁠ 1/2 ​ ⁠ ​ . Однако частота этой гетерозиготы = 1 , поскольку это F1 искусственного скрещивания: она возникла не в результате случайного оплодотворения. Поколение F2 было получено путем естественного самоопыления F1 (с контролем заражения насекомыми), в результате чего p = q = ⁠ 1 / 2 ⁠ поддерживается. Такой F2 называется «автогамным». Однако частоты генотипов (0,25 TT , 0,5 Tt , 0,25 tt ) возникли в результате системы спаривания, сильно отличающейся от случайного оплодотворения, и поэтому использования квадратичного расширения удалось избежать. Полученные числовые значения были такими же, как и для случайного оплодотворения, только потому, что это особый случай первоначального скрещивания гомозиготных противоположных родителей. Мы можем заметить, что из-за доминирования T- [частота (0,25 + 0,5)] над tt [частота 0,25] соотношение 3:1 все еще получается.

Скрещивание, подобное скрещиванию Менделя, при котором чистокровные (в основном гомозиготные) противоположные родители скрещиваются контролируемым образом для получения F1, является особым случаем гибридной структуры. F1 часто считают «полностью гетерозиготным» по рассматриваемому гену. Однако это чрезмерное упрощение и не применимо в целом — например, когда отдельные родители не гомозиготны или когда популяции подвергаются интергибридизации с образованием гибридных стаев . Общие свойства внутривидовых гибридов (F1) и F2 (как «автогамных», так и «аллогамных») рассматриваются в следующем разделе.

Самооплодотворение – альтернатива

Заметив, что горох естественно самоопыляется, мы не можем продолжать использовать его как пример для иллюстрации свойств случайного оплодотворения. Самоопыление («самопыление») — основная альтернатива случайному оплодотворению, особенно у растений. Большинство зерновых культур на Земле являются самоопыляемыми естественным путем (например, рис, пшеница, ячмень), а также бобовые. Учитывая миллионы особей каждого из них на Земле в любое время, очевидно, что самооплодотворение по меньшей мере столь же значимо, как и случайное оплодотворение. Самооплодотворение — наиболее интенсивная форма инбридинга , возникающая всякий раз, когда существует ограничение независимости генетического происхождения гамет. Такое снижение независимости возникает, если родители уже связаны родственниками, и/или из-за генетического дрейфа или других пространственных ограничений на распространение гамет. Анализ пути показывает, что это одно и то же. Исходя из этого, коэффициент инбридинга (часто обозначаемый как F или f ) количественно определяет эффект инбридинга по любой причине. Существует несколько формальных определений f , некоторые из них рассматриваются в последующих разделах. А пока заметим, что для многолетнего самооплодотворяющегося вида f = 1 . Однако естественные самооплодотворенные популяции представляют собой не отдельные « чистые линии », а смеси таких линий. Это становится особенно очевидным, если рассматривать одновременно более одного гена. Следовательно, частоты аллелей ( p и q ), отличные от 1 или 0, все еще актуальны в этих случаях (обратитесь к сечению Менделя). Однако частоты генотипов принимают другую форму.

В целом частоты генотипов становятся ${\textstyle [p^{2}(1-f)+pf]}$ для АА и ${\textstyle 2pq(1-f)}$ для Аа и ${\textstyle [q^{2}(1-f)+qf]}$ для аа .

Обратите внимание, что частота гетерозигот снижается пропорционально f . Когда f = 1 , эти три частоты становятся соответственно p , 0 и q. И наоборот, когда f = 0 , они сводятся к квадратичному разложению со случайным оплодотворением, показанному ранее.

Среднее значение численности населения

Среднее значение популяции смещает центральную точку отсчета от средней точки гомозиготы ( mp ) к среднему значению популяции, воспроизводимой половым путем. Это важно не только для того, чтобы перенести фокус на мир природы, но и для использования меры центральной тенденции, используемой статистикой/биометрией. В частности, квадрат этого среднего значения является поправочным фактором, который позже используется для получения генотипических отклонений.

Среднее значение населения по всем значениям p для различных эффектов d.

Поочередно для каждого генотипа эффект его аллеля умножается на частоту его генотипа; и продукты накапливаются по всем генотипам в модели. Для достижения краткого результата обычно следует некоторое алгебраическое упрощение.

Среднее значение после случайного оплодотворения

Вклад АА ​ ${\textstyle p^{2}(+)a}$ что Аа , ${\textstyle 2pqd}$, а aa значение ${\textstyle q^{2}(-)a}$. Собрав вместе два термина и суммируя все, мы получаем следующий результат: ${\textstyle a(p^{2}-q^{2})+2pqd}$. Упрощение достигается за счет того, что ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$и, напоминая, что ${\textstyle (p+q)=1}$, тем самым сводя правый член к ${\textstyle (p-q)}$.

Таким образом, краткий результат ${\textstyle G=a(p-q)+2pqd}$.

Это определяет среднее значение популяции как «смещение» от средней точки гомозиготы (напомним, что a и d определяются как отклонения от этой средней точки). На рисунке изображен G для всех значений p для нескольких значений d , включая один случай небольшого чрезмерного доминирования. Обратите внимание, что G часто отрицательна, тем самым подчеркивая, что она сама по себе является отклонением (от mp ).

Наконец, чтобы получить фактическое среднее значение численности населения в «фенотипическом пространстве», к этому смещению добавляется значение средней точки: ${\textstyle P=G+mp}$.

Примером могут служить данные о длине початков кукурузы. Предположим на данный момент, что представлен только один ген, a = 5,45 см, d = 0,12 см [фактически «0», на самом деле], mp = 12,05 см. Далее предположив, что p = 0,6 и q = 0,4 в этом примере совокупности, тогда:

G = 5,45 (0,6 – 0,4) + (0,48)0,12 = 1,15 см (округлено); и

Р =1,15+12,05= 13,20 см (округленно).

Среднее значение после длительного самооплодотворения

Вклад АА ​ ${\textstyle p(+a)}$, в то время аа как ${\textstyle q(-a)}$. [Частоты см. выше.] Объединение этих двух членов a сразу же приводит к очень простому конечному результату:

${\textstyle G_{(f=1)}=a(p-q)}$. Как и прежде, ${\textstyle P=G+mp}$.

Часто «G _(f=1) » сокращается до «G ₁ ».

Горох Менделя может предоставить нам аллельные эффекты и среднюю точку (см. ранее); а смешанная самоопыляемая популяция с p = 0,6 и q = 0,4 представляет собой пример частоты. Таким образом:

G _(f=1) = 82 (0,6-0,04) = 59,6 см (округленно); и

Р _(f=1) = 59,6 + 116 = 175,6 см (округленно).

Среднее значение – генерализованное оплодотворение

Общая формула включает коэффициент инбридинга f и может быть адаптирована к любой ситуации. Процедура точно такая же, как и раньше, с использованием взвешенных частот генотипов, приведенных ранее. После перевода в наши символы и дальнейшей перестановки:

$${\begin{aligned}G_{f}&=a(q-p)+[2pqd-f(2pqd)]\\&=a(p-q)+(1-f)2pqd\\&=G_{0}-f\ 2pqd\end{aligned}}$$Здесь G ₀ представляет собой G , указанный ранее. (Часто, когда речь идет об инбридинге, «G0 _» предпочтительнее «G».)

Предположим, что пример с кукурузой [приведенный ранее] был ограничен холмом (узким прибрежным лугом) и имел частичное инбридинг до степени f = 0,25 , затем, используя третью версию (выше) G _f :

Г _0,25 = 1,15 - 0,25 (0,48) 0,12 = 1,136 см (округлено), при Р _0,25 = 13,194 см (округлено).

В этом примере практически нет эффекта от инбридинга, который возникает из-за того, что по этому признаку практически не было доминирования ( d → 0). Анализ всех трех версий G _f показывает, что это приведет к тривиальному изменению среднего значения численности населения. Однако там, где доминирование было заметным, происходили значительные изменения.

Генетический дрейф

Генетический дрейф был введен при обсуждении вероятности того, что панмиксия широко распространена как естественный образец оплодотворения. [См. раздел «Частоты аллелей и генотипов».] Здесь выборка гамет из потенциальной гамодемы обсуждается более подробно. Выборка включает случайное оплодотворение между парами случайных гамет, каждая из которых может содержать либо аллель A , либо аллель a . Таким образом, выборка является биномиальной. Каждый «пакет» выборки включает 2N аллелей и дает N в результате зигот («потомство» или «линию»). В течение репродуктивного периода эта выборка повторяется снова и снова, так что конечным результатом является смесь потомков выборки. Результатом является рассеянное случайное внесение удобрений. $\left(\bigodot \right)$ Эти события и общий конечный результат рассматриваются здесь на наглядном примере.

«Базовые» частоты аллелей в примере соответствуют частотам потенциальной гамодемы : частота A равна p _g = 0,75 , а частота a равна q _g = 0,25 . [ Белая метка « 1 » на диаграмме.] Пять примеров реальных гамодем выбираются из этой базы биномиально ( s = количество выборок = 5), и каждый образец обозначается «индексом» k : с k = 1. ... последовательно. (Это «пакеты» выборки, упомянутые в предыдущем абзаце.) Число гамет, участвующих в оплодотворении, варьируется от образца к образцу и обозначается как 2N _k [в белой метке « 2 » на диаграмме). Общее (Σ) количество отобранных гамет составляет 52 ( белая метка « 3 » на диаграмме). Поскольку каждая выборка имеет свой размер, веса необходимы для получения средних значений (и других статистических данных) при получении общих результатов. Это ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$и обозначены белой меткой « 4 » на диаграмме.

Пример анализа генетического дрейфа.

Образец гамодем – генетический дрейф

После завершения этих пяти событий биномиальной выборки каждая результирующая фактическая гамодема содержала разные частоты аллелей — ( p _k и q _k ). [Они обозначены цифрой « 5 » на диаграмме.] Этот результат на самом деле является самим генетическим дрейфом. Обратите внимание, что два образца (k = 1 и 5) имеют те же частоты, что и базовая ( потенциальная ) гамодема. В другом (k = 3) p и q «перевернуты». Выборка (k = 2) представляет собой «крайний» случай: p _k = 0,9 и q _k = 0,1 ; в то время как оставшийся образец (k = 4) находится в «середине диапазона» частот аллелей. Все эти результаты возникли лишь «случайно», благодаря биномиальной выборке. Однако, возникнув, они закрепляют все последующие свойства потомков.

Поскольку выборка предполагает случайность, интерес представляют вероятности ( ∫ _k ) получения каждой из этих выборок. Эти биномиальные вероятности зависят от начальных частот ( p _g и q _g ) и размера выборки ( 2N _k ). Их утомительно получать, но представляют значительный интерес. [См. белую метку « 6 » на диаграмме.] Два образца (k = 1, 5) с частотами аллелей такими же, как и в потенциальной гамодеме , имели более высокие «шансы» возникновения, чем другие образцы. Однако их биномиальные вероятности различались из-за разного размера выборки (2N _k ). «Обратный» образец (k = 3) имел очень низкую вероятность возникновения, что, возможно, подтверждает то, что можно было ожидать. Однако «крайняя» гамодема частоты аллелей (k = 2) не была «редкой»; а выборка «среднего диапазона» (k=4) встречалась редко. Те же самые вероятности применимы и к потомству от этих оплодотворений.

Здесь некоторое подведение итогов можно начать . Общие частоты аллелей в основной массе потомков представляют собой средневзвешенные значения соответствующих частот отдельных образцов. То есть: ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ и ${\textstyle q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ q_{k}}$. (Обратите внимание, что k заменяется на • для общего результата — обычная практика.) Результаты для примера: p _• = 0,631 и q _• = 0,369 [ черная метка « 5 » на диаграмме]. Эти значения сильно отличаются от начальных ( p _g и q _g ) [ белая метка « 1 »]. Частоты аллелей в выборке также имеют как дисперсию, так и среднее значение. Это было получено с использованием суммы квадратов (SS). метода [Смотрите справа от черной метки « 5 » на схеме]. [Дальнейшее обсуждение этой разницы происходит в разделе «Обширный генетический дрейф» ниже.]

Потомственные линии – дисперсия

Частоты генотипов пяти выборочных потомков получены путем обычного квадратичного разложения соответствующих частот аллелей ( случайное оплодотворение ). » на диаграмме Результаты приведены на белой метке « 7 для гомозигот и на белой метке « 8 » для гетерозигот. Такая реорганизация готовит почву для мониторинга уровня инбридинга. Это можно сделать либо путем исследования уровня тотальной гомозиготности [( p ² _к + д ² _k ) = ( 1 - 2p _k q _k )] , или путем изучения уровня гетерозиготности ( 2p _k q _k ), поскольку они дополняют друг друга. Обратите внимание, что образцы k = 1, 3, 5 имели одинаковый уровень гетерозиготности, несмотря на то, что один из них был «зеркальным отражением» других в отношении частот аллелей. Случай «крайней» частоты аллелей (k = 2 ) имел наибольшую гомозиготность (наименьшую гетерозиготность) среди всех образцов. Случай «среднего диапазона» (k = 4 ) имел наименьшую гомозиготность (наибольшую гетерозиготность): фактически каждый из них был равен 0,50.

Общий итог можно продолжить получением средневзвешенного значения соответствующих частот генотипов для массы потомства. Таким образом, для АА это ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$, для Аа это ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ и для аа это ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$. Результаты примера даны с черной меткой « 7 » для гомозигот и с черной меткой « 8 » для гетерозигот. Обратите внимание, что среднее значение гетерозиготности составляет 0,3588 , которое в следующем разделе используется для изучения инбридинга, возникшего в результате этого генетического дрейфа.

Следующим объектом интереса является сама дисперсия, которая относится к «распространению» популяционных средств потомства . Они получены как ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ [см. раздел «Среднее значение популяции») для каждого выборочного потомства по очереди, используя примеры эффектов генов, указанные под белой меткой « 9 » на диаграмме. Затем каждый ${\textstyle P_{k}=G_{k}+mp}$ также получается [по белой метке « 10 » на диаграмме]. Обратите внимание, что «лучшая» линия (k = 2) имела самую высокую частоту аллеля для «большего» аллеля ( А ) (она также имела самый высокий уровень гомозиготности). Худшее потомство (k = 3) имело самую высокую частоту «меньшего» аллеля ( a ), что и объясняло его плохие характеристики. Эта «бедная» линия была менее гомозиготной, чем «лучшая» линия; и фактически он имел тот же уровень гомозиготности, что и две вторые лучшие линии (k = 1, 5). Линия потомства, в которой аллели «больше» и «меньше» присутствовали с одинаковой частотой (k = 4), имела среднее значение ниже общего среднего (см. Следующий параграф) и имела самый низкий уровень гомозиготности. Эти результаты показывают тот факт, что аллели, наиболее распространенные в «генном фонде» (также называемом «зародышевой плазмой»), определяют производительность, а не уровень гомозиготности как таковой. Только биномиальная выборка влияет на эту дисперсию.

теперь Общий итог можно подвести, получив ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ и ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$. Пример результата для P _• равен 36,94 ( черная метка « 10 » на диаграмме). Позже это используется для количественной оценки общей инбридинговой депрессии на основе выборки гамет. [См. следующий раздел.] Однако вспомните, что некоторые «недепрессивные» средства потомства уже идентифицированы (k = 1, 2, 5). Это загадка инбридинга: хотя в целом может наблюдаться «депрессия», среди выборок гамодем обычно есть превосходящие линии.

Эквивалент пост-расселенной панмиктики – инбридинг.

В общий итог были включены средние частоты аллелей в смеси линий потомства ( p _* и q _* ). Теперь их можно использовать для создания гипотетического панмиктического эквивалента. Это можно рассматривать как «эталон» для оценки изменений, вызванных отбором проб гамет. В примере такая панмиктика добавляется справа от диаграммы. частота АА Следовательно, равна (p _• ) ² = 0,3979. Это меньше, чем в дисперсной массе (0,4513 по черной метке « 7 »). Аналогично для aa , (q _• ) ² = 0,1303 – опять меньше эквивалента в массе потомков (0,1898). Видно, что генетический дрейф увеличил общий уровень гомозиготности на величину (0,6411 - 0,5342) = 0,1069. В дополнительном подходе вместо этого можно использовать гетерозиготность. Панмиктический эквивалент Аа составляет 2 p _• q _• = 0,4658, что выше , чем в выборочной массе (0,3588) [ черная метка « 8 »]. Выборка привела к уменьшению гетерозиготности на 0,1070, что незначительно отличается от предыдущей оценки из-за ошибок округления.

Коэффициент инбридинга ( f ) был введен в начале раздела о самооплодотворении. Здесь рассматривается его формальное определение: f — это вероятность того, что две «одинаковые» аллели (то есть A и A или a и a ), которые оплодотворяются вместе, имеют общее наследственное происхождение, или (более формально) f — это вероятность того, что два гомологичных аллеля являются автозиготными. Рассмотрим любую случайную гамету в потенциальной гамодеме, партнер по сингамии которой ограничен биномиальной выборкой. Вероятность того, что вторая гамета является гомологичной автозиготной первой, равна 1/(2N) — обратной величине размера гамодемы. Для пяти примеров потомства эти количества составляют 0,1, 0,0833, 0,1, 0,0833 и 0,125 соответственно, а их средневзвешенное значение составляет 0,0961 . Это коэффициент инбридинга для массы образцовых потомков, при условии, что он несмещен по отношению к полному биномиальному распределению. Однако пример, основанный на s = 5 , вероятно, будет предвзятым по сравнению с подходящим полным биномиальным распределением, основанным на количестве выборки ( s ), приближающемся к бесконечности ( s → ∞ ). Другое производное определение f для полного распределения состоит в том, что f также равно увеличению гомозиготности, что равно падению гетерозиготности. Для примера эти изменения частоты составляют 0,1069 и 0,1070 соответственно. Этот результат отличается от приведенного выше и указывает на то, что в примере присутствует смещение по отношению к полному базовому распределению. примера Для самого лучше использовать последние значения, а именно f _• = 0,10695 .

Среднее популяционное значение эквивалентного панмиктика находится как [a (p _• -q _• ) + 2 p _• q _• d] + mp . Используя пример эффектов генов ( белая метка « 9 » на диаграмме), это среднее значение равно ${\textstyle P_{\centerdot }=}$ 37.87. Эквивалентное среднее значение в дисперсной массе равно 36,94 ( черная метка « 10 »), что понижено на величину 0,93 . Это инбридинговая депрессия, вызванная генетическим дрейфом. Однако, как отмечалось ранее, три потомства не были депрессивными (k = 1, 2, 5) и имели даже более высокие значения, чем у панмиктического эквивалента. Это те линии, которые селекционер ищет в программе селекции линий.

Обширная биномиальная выборка – восстанавливается ли панмиксия?

Если количество биномиальных выборок велико ( s → ∞ ), то p _• → p _g и q _• → q _g . Можно задаться вопросом, действительно ли панмиксия вновь появится в этих обстоятельствах. Однако выборка частот аллелей , все же произошла в результате чего σ ² _{п, д} ≠ 0 . Действительно, при s → ∞ ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$, что является дисперсией всего биномиального распределения . Более того, «уравнения Валунда» показывают, что частоты гомозигот по массе потомства могут быть получены как суммы их соответствующих средних значений ( p ² _• или q ² _• ) плюс σ ² _{п, д} . Аналогично, общая частота гетерозигот равна (2 p _• q _• ) минус удвоенная σ . ² _{п, д} . Заметно присутствует дисперсия, возникающая в результате биномиальной выборки. Таким образом, даже когда s → ∞ потомства , частоты генеральных генотипов по-прежнему обнаруживают повышенную гомозиготность и снижение гетерозиготности , все еще существует дисперсия средств потомства и все еще инбридинг и инбредная депрессия . То есть панмиксия не достигается повторно после потери из-за генетического дрейфа (биномиальная выборка). Однако новая потенциальная панмиксия может быть инициирована посредством аллогамного F2 после гибридизации.

Продолжающийся генетический дрейф – усиление дисперсии и инбридинга

Предыдущее обсуждение генетического дрейфа рассматривало только один цикл (поколение) этого процесса. Когда выборка продолжается в течение последующих поколений, происходят заметные изменения в σ. ² _{п , д} и ж . Кроме того, для отслеживания «времени» необходим еще один «индекс»: t = 1 .... y , где y = количество рассматриваемых «лет» (поколений). Методика часто заключается в добавлении текущего биномиального приращения ( Δ = « de novo ») к тому, что произошло ранее. Здесь рассматривается все биномиальное распределение. [Нет никакой дополнительной пользы от сокращенного примера.]

Дисперсия через σ ² _{п, д}

Ранее эта дисперсия (σ ² _{п, д} ) было замечено как: - $${\begin{aligned}\sigma _{p,q}^{2}&=p_{g}q_{g}\ /\ 2N\\&=p_{g}q_{g}\left({\frac {1}{2N}}\right)\\&=p_{g}q_{g}\ f\\&=p_{g}q_{g}\ \Delta f\ \scriptstyle {\text{when used in recursive equations}}\end{aligned}}$$

С расширением во времени это тоже результат первого цикла, и так ${\textstyle \sigma _{1}^{2}}$ (для краткости). В цикле 2 эта дисперсия генерируется еще раз — на этот раз она становится дисперсией de novo ( ${\textstyle \Delta \sigma ^{2}}$) — и накапливается до того, что уже присутствовало — «переходящей» дисперсии. Вторая дисперсия цикла ( ${\textstyle \sigma _{2}^{2}}$) представляет собой взвешенную сумму этих двух компонентов, причем веса равны ${\textstyle 1}$ для de novo и ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ = ${\textstyle \left(1-\Delta f\right)}$ за «перенос».

Таким образом,

$\sigma _{2}^{2}=\left(1\right)\ \Delta \sigma ^{2}+\left(1-\Delta f\right)\sigma _{1}^{2}$ ( 1 )

Расширение для обобщения на любое время t после значительного упрощения становится следующим: -

$\sigma _{t}^{2}=p_{g}q_{g}\left[1-\left(1-\Delta f\right)^{t}\right]$ ( 2 )

Поскольку именно это изменение частот аллелей вызвало «разброс» средних потомков ( дисперсию ), изменение σ ² _t по поколениям указывает на изменение уровня дисперсии .

Дисперсия через f

Метод исследования коэффициента инбридинга аналогичен методу, использованному для σ ² _{п, q} . Те же веса, что и раньше, используются соответственно для de novo f ( Δ f ) [напомним, что это 1/(2N) ] и переноса f . Поэтому, ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ , что аналогично уравнению (1) в предыдущем подразделе.

Инбридинг, возникающий в результате генетического дрейфа при случайном оплодотворении.

В общем, после перестановки $${\begin{aligned}f_{t}&=\Delta f+\left(1-\Delta f\right)f_{t-1}\\&=\Delta f\left(1-f_{t-1}\right)+f_{t-1}\end{aligned}}$$ Графики слева показывают уровни инбридинга в двадцати поколениях, возникающие в результате генетического дрейфа для различных фактических размеров гамодем (2N).

Дальнейшие перестановки этого общего уравнения выявляют некоторые интересные зависимости.

(А) После некоторого упрощения ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$. Левая часть представляет собой разницу между текущим и предыдущим уровнями инбридинга: изменение инбридинга ( δf _t ). Обратите внимание, что это изменение инбридинга ( δf _t ) равно инбридингу de novo ( Δf ) только для первого цикла — когда f _t-1 равно нулю .

(B) Следует отметить (1-f _t-1 ) , который является «индексом отсутствия инбридинга ». Он известен как панмиктический индекс . ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$.

(C) Возникают дальнейшие полезные зависимости, связанные с панмиктическим индексом . $${\begin{aligned}\Delta f&={\frac {\delta f_{t}}{P_{t-1}}}\\&=1-{\frac {P_{t}}{P_{t-1}}}\end{aligned}}$$. (D) Ключевая связь возникает между σ ² _p,q и f . Во-первых... $${\begin{aligned}f_{t}&=1-\left(1-1\Delta f\right)^{t}\left(1-f_{0}\right)\end{aligned}}$$Во-вторых, предполагая, что f ₀ = 0 , правая часть этого уравнения сводится к разделу в скобках уравнения (2) в конце последнего подраздела. То есть, если изначально инбридинга нет, ${\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}$ ! Кроме того, если это затем переставить, ${\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}$. То есть, когда начальный инбридинг равен нулю, две основные точки зрения на биномиальную выборку гамет (генетический дрейф) напрямую взаимоконвертируются.

Самоопыление при случайном оплодотворении

Случайное оплодотворение по сравнению с перекрестным оплодотворением

Легко упустить из виду, что случайное оплодотворение включает и самооплодотворение. Сьюэлл Райт показал, что доля 1/N случайных оплодотворений на самом деле является самооплодотворением. $\left(\bigotimes \right)$, а остаток (N-1)/N представляет собой перекрестное оплодотворение. $\left({\mathsf {X}}\right)$. После анализа пути и упрощения было обнаружено, что новый взгляд на инбридинг со случайным оплодотворением выглядит следующим образом: ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$. При дальнейшей перестановке были подтверждены предыдущие результаты биномиальной выборки, а также некоторые новые схемы. Два из них были потенциально очень полезны, а именно: (А) ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$; и (Б) ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$.

Признание того, что самоопыление по своей сути может быть частью случайного оплодотворения, приводит к некоторым проблемам, связанным с использованием предыдущего случайного оплодотворения «коэффициента инбридинга» . Очевидно, что он не подходит для любых видов, неспособных к самооплодотворению , включая растения с механизмами самонесовместимости, двудомные растения и двуполые животные . Уравнение Райта позже было изменено, чтобы обеспечить версию случайного оплодотворения, которая включала только перекрестное оплодотворение без самооплодотворения . Пропорция 1/N, ранее возникшая в результате самоопыления, теперь определяла перенос генного дрейфа инбридинга, возникший в результате предыдущего цикла. Новая версия: $$f_{{\mathsf {X}}_{t}}=f_{t-1}+\Delta f\left(1+f_{t-2}-2f_{t-1}\right)$$.

справа показаны различия между стандартным случайным оплодотворением RF и случайным оплодотворением с поправкой на «только перекрестное оплодотворение» CF. На графиках Как можно видеть, проблема нетривиальна для небольших размеров выборки гамодем.

Теперь необходимо отметить, что не только «панмиксия» не является синонимом «случайного оплодотворения», но и что «случайное оплодотворение» не является синонимом «перекрестного оплодотворения».

Гомозиготность и гетерозиготность

В подразделе «Выборка гамодем – Генетический дрейф» была проведена серия выборок гамет, результатом которых стало увеличение гомозиготности за счет гетерозиготности. С этой точки зрения повышение гомозиготности произошло за счет выборок гамет. Уровни гомозиготности можно рассматривать также по тому, возникли ли гомозиготы аллозиготно или автозиготно. Напомним, что автозиготные аллели имеют одинаковое аллельное происхождение, вероятность (частота) которого является коэффициентом инбридинга ( f ) по определению. Таким образом, доля, возникающая аллозиготно, равна (1-f) . для гамет, несущих А , общая частота которых равна p , общая частота автозиготных гамет равна ( fp Таким образом , ). Аналогично, для гамет, несущих a , автозиготная частота равна ( f q ). Эти две точки зрения относительно частоты генотипов должны быть связаны, чтобы обеспечить согласованность.

Следуя в первую очередь точке зрения auto/allo , рассмотрим аллозиготный компонент. Это происходит с частотой (1-f) , и аллели объединяются в соответствии с квадратичным расширением случайного оплодотворения . Таким образом: $$\left(1-f\right)\left[p_{0}+q_{0}\right]^{2}=\left(1-f\right)\left[p_{0}^{2}+q_{0}^{2}\right]+\left(1-f\right)\left[2p_{0}q_{0}\right]$$ Далее рассмотрим автозиготный компонент. Поскольку эти аллели являются автозиготными , они фактически являются самоопыляющимися и производят генотипы АА или АА , но не гетерозиготы. Поэтому они производят ${\textstyle fp_{0}}$ «АА» гомозиготы плюс ${\textstyle fq_{0}}$ «аа» гомозиготы. Объединение этих двух компонентов вместе приводит к: ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ для гомозиготы АА ; ${\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}$ для гомозиготы аа ; и ${\textstyle \left(1-f\right)2p_{0}q_{0}}$ для гетерозиготы Аа . Это то же уравнение, что и представленное ранее в разделе «Самооплодотворение – альтернатива». Здесь становится ясной причина снижения гетерозиготности. Гетерозиготы могут возникнуть только из аллозиготного компонента, и его частота в массе выборки равна всего (1-f) : следовательно, это также должно быть фактором, контролирующим частоту гетерозигот.

Во-вторых, выборки пересматривается точка зрения . Ранее отмечалось, что снижение числа гетерозигот было ${\textstyle f\left(2p_{0}q_{0}\right)}$. Это снижение равномерно распределяется среди каждой гомозиготы; и добавляется к их основным ожиданиям случайного оплодотворения . Таким образом, частоты генотипов составляют: ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ для гомозиготы «АА» ; ${\textstyle \left(q_{0}^{2}+fp_{0}q_{0}\right)}$ для гомозиготы «аа» ; и ${\textstyle 2p_{0}q_{0}-f\left(2p_{0}q_{0}\right)}$ для гетерозиготы.

В-третьих, необходимо установить соответствие между двумя предыдущими точками зрения. Сразу видно [из соответствующих уравнений, приведенных выше], что частота гетерозигот одинакова с обеих точек зрения. Однако такой простой результат не сразу очевиден для гомозигот. Начните с рассмотрения АА окончательного уравнения гомозиготы в параграфе auto/allo выше: ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$. Раскройте скобки и затем заново соберите [в пределах результирующего] два новых члена с общим множителем f в них. Результат: ${\textstyle p_{0}^{2}-f\left(p_{0}^{2}-p_{0}\right)}$. Далее, для заключенного в скобки " p ² ₀ ", a (1-q) заменяется на p , результат становится ${\textstyle p_{0}^{2}-f\left[p_{0}\left(1-q_{0}\right)-p_{0}\right]}$. После этой замены остается простой вопрос умножения, упрощения и наблюдения за знаками. Конечный результат ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$, что в точности соответствует результату для АА в разделе выборки . Таким образом, обе точки зрения согласуются в отношении гомозиготы АА . последовательность точек зрения аа Подобным же образом можно также продемонстрировать . Обе точки зрения едины для всех классов генотипов.

Расширенные принципы

Другие схемы внесения удобрений

Пространственные схемы внесения удобрений

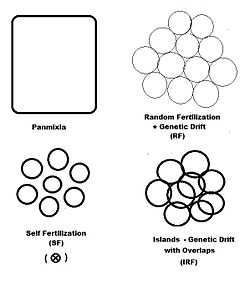
В предыдущих разделах всесторонне рассматривалось дисперсионное случайное оплодотворение ( генетический дрейф ), а также в различной степени исследовались самооплодотворение и гибридизация. На диаграмме слева изображены первые два из них, а также еще один «пространственный» шаблон: острова . Это образец случайного оплодотворения , включающий рассредоточенные гамодемы с добавлением «перекрытий», при которых происходит недисперсионное случайное оплодотворение. При островковом отдельные размеры гамодем ( 2N узоре наблюдаются ), а перекрытия ( m ) минимальны. Это одна из возможностей Сьюэлла Райта. Помимо «пространственных» моделей оплодотворения, существуют и другие, основанные на «фенотипических» критериях или критериях «родства». К фенотипическим основам относятся ассортативное оплодотворение (между сходными фенотипами) и дисассортативное оплодотворение (между противоположными фенотипами). Паттерны взаимоотношений включают скрещивание сибсов , кузенов и обратное скрещивание — и рассматриваются в отдельном разделе. Самооплодотворение можно рассматривать как с пространственной точки зрения, так и с точки зрения отношений.

«Острова» случайного оплодотворения

Гнездящаяся популяция состоит из небольших , рассеянных гамодем, произведённых методом случайного оплодотворения размер выборки ${\textstyle 2N_{k}}$ ( k = 1 ... s ) с « перекрытиями » пропорций ${\textstyle m_{k}}$ при котором происходит недисперсионное случайное оплодотворение . Дисперсионная пропорция , таким образом, равна ${\textstyle \left(1-m_{k}\right)}$. Основная популяция состоит из средневзвешенных размеров выборки, частот аллелей и генотипов и средних значений потомства, как это было сделано для генетического дрейфа в предыдущем разделе. Однако размер выборки каждой гаметы уменьшается, чтобы учесть перекрытие , таким образом находя ${\textstyle 2N_{k}}$ эффективен для ${\textstyle \left(1-m_{k}\right)}$.

«Острова» случайного оплодотворения

Для краткости аргумент следует далее без индексов. Напомним, что ${\textstyle {\tfrac {1}{2N}}}$ является ${\textstyle \Delta f}$ в общем. [Здесь и далее 2N относится к ранее определенному размеру выборки, а не к какой-либо версии, «скорректированной на острова».]

После упрощения $$^{\mathsf {islands}}\Delta f={\frac {\left(1-m\right)^{2}}{2N-m^{2}\left(2N-1\right)}}$$ Обратите внимание, что когда m = 0, это уменьшается до предыдущего Δ f . Обратное к этому значение дает оценку « ${\textstyle 2N_{k}}$ эффективен для ${\textstyle \left(1-m_{k}\right)}$ ", упоминалось выше.

Это Δf также подставляется в предыдущий коэффициент инбридинга , чтобы получить $${^{\mathsf {islands}}f_{t}}=\ {^{\mathsf {islands}}\Delta f_{t}}+\left(1-\ {^{\mathsf {islands}}\Delta f_{t}}\right)\ {^{\mathsf {islands}}f_{t-1}}$$ где t — индекс по поколениям, как и раньше.

Эффективную пропорцию перекрытия можно также получить, как $$m_{t}=1-\left[{\frac {2N\ {^{\mathsf {islands}}\Delta f_{t}}}{\left(2N-1\right)\ {^{\mathsf {islands}}\Delta f_{t}+1}}}\right]^{\tfrac {1}{2}}$$

Графики справа показывают инбридинг для размера гамодемы 2N = 50 для обычного рассеянного случайного оплодотворения (RF) (m=0) и для четырех уровней перекрытия (m = 0,0625, 0,125, 0,25, 0,5) островов . случайного оплодотворения . Действительно, произошло сокращение инбридинга в результате нерассредоточенного случайного оплодотворения при перекрывании. Это особенно заметно, поскольку m → 0,50 . Сьюэлл Райт предположил, что это значение должно быть пределом использования этого подхода.

Перетасовка аллелей – замена аллелей

Генная модель рассматривает путь наследственности с точки зрения «входов» (аллели/гаметы) и «выходов» (генотипы/зиготы), при этом оплодотворение является «процессом» преобразования одного в другое. Альтернативная точка зрения концентрируется на самом «процессе» и считает, что генотипы зигот возникают в результате перетасовки аллелей. В частности, он рассматривает результаты так, как если бы один аллель «заместил» другой во время перетасовки, вместе с остатком, который отклоняется от этой точки зрения. Это составляло неотъемлемую часть метода Фишера. в дополнение к использованию частот и эффектов для создания своей генетической статистики. Далее следует дискурсивный вывод альтернативы замены аллелей .

Анализ замены аллелей

Предположим, что обычное случайное оплодотворение гамет в «базовой» гамодеме, состоящей из p гамет ( A ) и q гамет ( a ), заменяется оплодотворением «наводнением» гамет, содержащих одну аллель ( A или a , но не оба). Результаты зиготики можно интерпретировать как аллель «затопления», «заменившую» альтернативную аллель в лежащей в основе «базовой» гамодеме. Следовать этой точке зрения помогает диаграмма: верхняя часть изображает замену А , а нижняя часть показывает замену . (Аллель RF на диаграмме — это аллель «базовой» гамодемы.)

Сначала рассмотрим верхнюю часть. Поскольку основание A присутствует с частотой p , заменитель A оплодотворяет его с частотой p, в результате чего образуется зигота AA с аллельным эффектом a . Таким образом, его вклад в результат – это продукт ${\textstyle \left(p\ a\right)}$. Аналогично, когда заменитель оплодотворяет основание a (что приводит к Aa с частотой q и гетерозиготным эффектом d ), вклад равен ${\textstyle \left(q\ d\right)}$. общий результат замены на А равен: Таким образом, ${\textstyle \left(p\ a+q\ d\right)}$. Теперь это ориентировано на среднее значение генеральной совокупности [см. предыдущий раздел], выражая его как отклонение от этого среднего значения: ${\textstyle \left(p\ a+q\ d\right)-G}$

После некоторого алгебраического упрощения это становится $$\beta _{A}=q\ \left[a+\left(q-p\right)d\right]$$ - замещения А. ​ эффект

Аналогичные рассуждения можно применить к нижней части диаграммы, учитывая различия в частотах и ​​эффектах генов. Результатом является эффект замещения a , который $$\beta _{a}=-\ p\left[a+\left(q-p\right)d\right]$$Общим фактором внутри скобок является средний эффект замены аллеля , и есть $$\beta =a+\left(q-p\right)d$$Его можно получить и более прямым путем, но результат тот же.

В последующих разделах эти эффекты замены помогают определить генотипы генной модели как состоящие из разделения, предсказанного этими новыми эффектами ( замены ожидания ), и остатка ( отклонения замены ) между этими ожиданиями и предыдущими эффектами генной модели. Ожидания , также называются племенными ценностями а отклонения также называются отклонениями доминирования .

В конечном итоге дисперсия, возникающая в результате ожиданий замены, становится так называемой аддитивной генетической дисперсией (σ ² _А ) (также генная вариация ) — а возникающая в результате отклонений замещения становится так называемой дисперсией доминирования (σ ² _Д ) . Примечательно, что ни один из этих терминов не отражает истинного значения этих отклонений. «Генная вариативность » менее сомнительна, чем аддитивная генетическая вариативность , и больше соответствует собственному названию Фишера для этого раздела. Менее вводящее в заблуждение название дисперсии отклонений доминирования — «дисперсия квазидоминирования» (см. дальнейшее обсуждение в следующих разделах). Эти последние термины являются здесь предпочтительными.

Переопределение эффектов генов

Эффекты генной модели ( a , d и -a ) вскоре станут важными при выводе отклонений от замены , которые впервые обсуждались в предыдущем разделе «Замена аллелей» . Однако их необходимо переопределить, прежде чем они станут полезными в этом упражнении. Во-первых, их необходимо повторно централизовать вокруг среднего значения популяции ( G ), а во-вторых, их необходимо перестроить в зависимости от β , среднего эффекта замены аллеля .

Рассмотрим в первую очередь рецентрализацию. Рецентрализованный эффект для AA равен a• = a - G , который после упрощения становится a• = 2 q (a- p d) . Аналогичный эффект для Aa равен d• = d - G = a( q - p ) + d(1-2 pq ) после упрощения. Наконец, эффект рецентрализации для aa равен (-a)• = -2 p (a+ q d) .

Во-вторых, рассмотрим перераспределение этих рецентрализованных эффектов в зависимости от β . Вспоминая из раздела «Замена аллелей», что β = [a +(qp)d], перегруппировка дает a = [β -(qp)d] . После замены этого на a в a• и упрощения окончательная версия становится a•• = 2q(β-qd) . Аналогично, d• становится d•• = β(qp) + 2pqd ; и (-a)• становится (-a)•• = -2p(β+pd) .

Замена генотипа – ожидания и отклонения

Генотипы зигот являются целью всей этой подготовки. Гомозиготный генотип АА представляет собой объединение двух эффектов замещения А , по одному от каждого пола. его ожидание замены Следовательно, равно β _AA = 2β _A = 2 q β (см. предыдущие разделы). Аналогично, ожидание замены Aa равно β + _Aa = β _A β _a = ( q - p )β ; для аа а β _аа = 2β _а = -2 п β . Эти ожидания замены генотипов также называются племенной ценностью .

Отклонения замещения — это различия между этими ожиданиями и эффектами генов после их двухэтапного переопределения в предыдущем разделе. Следовательно, d _AA = a•• - β _AA = -2 q ² д после упрощения. Аналогично, d _Aa = d•• - β _Aa = 2 pq d после упрощения. Наконец, d _aa = (-a)•• - β _aa = -2 p ² д после упрощения. Обратите внимание, что все эти отклонения от замены в конечном итоге являются функциями генного эффекта d , который объясняет использование ["d" плюс нижний индекс] в качестве их символов. Однако было бы серьезным логическим нарушением рассматривать их как причину доминирования (гетерозиготности) во всей генной модели: это просто функции «d», а не проверка «d» в системе. Они такие же, как и производные: отклонения от ожиданий замещения !

«Ожидания замещения» в конечном итоге приводят к возникновению σ ² _А (так называемая «аддитивная» генетическая изменчивость); а «отклонения замещения» приводят к σ ² _D (так называемая генетическая вариация «доминирования»). Однако имейте в виду, что средний эффект замещения (β) также содержит «d» [см. предыдущие разделы], что указывает на то, что доминирование также включено в «аддитивную» дисперсию (их выводы см. в следующих разделах, посвященных генотипической дисперсии). Помните также [см. предыдущий параграф], что «отклонения замещения» не объясняют доминирование в системе (представляя собой не что иное, как отклонения от ожиданий замещения ), но которые алгебраически состоят из функций «d». Более подходящими названиями для этих соответствующих отклонений могли бы быть σ. ² _B (дисперсия «ожиданий размножения») и σ ² _δ (дисперсия «Селекционные отклонения»). Однако, как отмечалось ранее, «Геник» (σ ² _А ) и «Квази-доминирование» (σ ² _D ), соответственно, будут здесь предпочтительными.

Генотипическая дисперсия

Существует два основных подхода к определению и распределению генотипической вариативности . Один из них основан на эффектах генной модели , в то время как другой основан на эффектах замены генотипа Они алгебраически взаимоконвертируемы друг с другом. В этом разделе рассматривается основной процесс случайного оплодотворения , без учета эффектов инбридинга и дисперсии. Это будет рассмотрено позже, чтобы прийти к более общему решению. До тех пор, пока это моногенное лечение не будет заменено мультигенным и пока эпистаз не будет решен в свете результатов эпигенетики , генотипическая дисперсия имеет только компоненты, рассматриваемые здесь.

Подход генной модели – Мэзер Джинкс Хейман

Компоненты генотипической дисперсии с использованием эффектов генной модели.

Удобно следовать биометрическому подходу, который основан на корректировке нескорректированной суммы квадратов (USS) путем вычитания поправочного коэффициента (CF) . Поскольку все эффекты были рассмотрены с помощью частот, USS можно получить как сумму произведений «частоты каждого генотипа» и квадрата его генного эффекта . CF в данном случае является среднеквадратическим. В результате получается СС, который, опять же из-за использования частот, также сразу же является дисперсией .

The ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$и ${\textstyle {\mathsf {CF}}={\mathsf {G}}^{2}}$. ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$

После частичного упрощения $${\begin{aligned}\sigma _{G}^{2}&=2pqa^{2}+(q-p)4pqad+2pqd^{2}+(2pq)^{2}d^{2}\\&=\sigma _{a}^{2}+({\text{weighted-covariance}})_{ad}+\sigma _{d}^{2}+\sigma _{D}^{2}\\&={\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{1}+{\tfrac {1}{4}}{\mathsf {H}}_{2}\end{aligned}}$$ Последняя строка взята из терминологии Мэзера.

Здесь σ ² _a - гомозигота или аллельная дисперсия, а σ ² _d - гетерозигота или дисперсия доминирования . Дисперсия отклонений замещения ( σ ² _Д ) тоже присутствует. Объявление ) _{( взвешенная_ковариация} далее сокращенно « cov _ad ».

Эти компоненты отображены на графике для всех значений p на прилагаемом рисунке. Обратите внимание, что cov _ad имеет отрицательное значение при p > 0,5 .

На большинство этих компонентов влияет изменение центрального фокуса от средней точки гомозиготы ( mp ) к среднему значению популяции ( G ), причем последнее является основой поправочного фактора . Дисперсии COV _{отклонения от} и замещения являются просто артефактами этого сдвига. Аллельные вариации являются подлинными генетическими разделами исходной генной модели и являются и доминантные единственными эвгенетическими компонентами. Даже в этом случае на алгебраическую формулу аллельной дисперсии влияет присутствие G : это только дисперсия доминирования (т.е. σ ² _d на который не влияет переход от mp к G. ) , Эти идеи обычно не оцениваются по достоинству.

Дальнейший сбор терминов [в формате Mather] приводит к ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$, где ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$. Это полезно позже при анализе Диаллеля, который представляет собой экспериментальную схему оценки этой генетической статистики.

Если после последних перестановок первые три члена объединяются вместе, переставляются дальше и упрощаются, результатом является дисперсия ожидания замены Фишера .

То есть: $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$

Особо отметим, что σ ² _А не σ ² _а . Первый — это дисперсия ожиданий замены , а второй — аллельная дисперсия. Заметим также, что σ ² _D ( дисперсия отклонений замещения ) не равна σ ² _d ( дисперсия доминирования ), и напомним, что это артефакт, возникающий из-за использования G в качестве поправочного коэффициента. [См. «синий абзац» выше.] Теперь это будет называться дисперсией «квазидоминирования».

Также отметим, что σ ² _Д < σ ² _d («2pq» всегда является дробью); и заметим, что (1) σ ² _D = 2pq σ ² _d и что (2) σ ² _д = п ² _Д /(2пк) . То есть: подтверждено, что σ ² _D не дает количественной оценки дисперсии доминирования в модели. Это σ ² _d, который это делает. Однако дисперсия доминирования (σ ² _d ) можно легко оценить по σ ² _D , если 2pq доступен .

Судя по рисунку, эти результаты можно визуализировать как накопление σ ² _а , п ² _d и cov _ad , чтобы получить σ ² _A , оставляя σ ² _Буду все еще расставаться. Из рисунка также видно, что σ ² _Д < σ ² _d , как и ожидалось из уравнений.

Общий результат (в формате Фишера) равен $${\begin{aligned}\sigma _{G}^{2}&=2pq\left[a+(q-p)d\right]^{2}+\left(2pq\right)^{2}d^{2}\\&=\sigma _{A}^{2}+\sigma _{D}^{2}\\&=\left[\left(\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}\right)\right]+\left[2pq\ \sigma _{d}^{2}\right]\end{aligned}}$$ Компоненты Фишера только что были выведены, но их вывод через сами эффекты замещения также дан в следующем разделе.

Подход аллель-замещения - Фишер

Компоненты генотипической дисперсии с использованием эффектов аллель-замены.

Ссылка на несколько предыдущих разделов, посвященных замене аллелей, показывает, что двумя окончательными эффектами являются ожидания замены генотипа и отклонения замены генотипа . Обратите внимание, что каждый из них уже определен как отклонения от среднего значения случайной популяции оплодотворения ( G ). Таким образом, для каждого генотипа по очереди получается произведение частоты и квадрата соответствующего эффекта, и они суммируются для непосредственного получения SS и σ. ² . Подробности следуют.

п ² _А = п ² β _АА ² + 2 pq β _Аа ² + д ² β _аа ² , что упрощается до σ ² _А = 2 pq β ² — Генная вариация.

п ² _Д = п ² д _АА ² + 2 шт. д _Аа ² + q д _аа ² , что упрощается до σ ² _Д = (2 пк ) ² д ² – дисперсия квазидоминирования.

Суммируя эти результаты, σ ² _г = п ² _А + р ² _Д. ​Эти компоненты визуализируются на графиках справа. Средний эффект замены аллеля также представлен на графике, но символом является «α» (как принято в цитатах), а не «β» (как используется здесь).

Однако еще раз обратимся к предыдущим дискуссиям об истинных значениях и идентичности этих компонентов. Сам Фишер не использовал эти современные термины для своих компонентов. Дисперсию ожиданий замены он назвал «генетической» дисперсией; а дисперсию отклонений замещения он рассматривал просто как неназванный остаток между «генотипической» дисперсией (его название для нее) и его «генетической» дисперсией. [Терминология и вывод, использованные в этой статье, полностью соответствуют терминологии Фишера.] Термин Мэзера для обозначения ожиданий дисперсии — «генный». - очевидно, происходит от термина Фишера и избегает использования слова «генетический» (которое стало слишком общим в использовании, чтобы иметь ценность в данном контексте). Происхождение современных вводящих в заблуждение терминов «аддитивная» и «доминантная» дисперсия неясно.

Обратите внимание, что этот подход с аллель-заменой определял компоненты отдельно, а затем суммировал их для получения окончательной генотипической дисперсии. И наоборот, подход генной модели вывел всю ситуацию (компоненты и сумму) как одно упражнение. Бонусами, вытекающими из этого, были: (а) открытие реальной структуры σ ² _A и (b) реальные значения и относительные размеры σ ² _d и σ ² _D (см. предыдущий подраздел). Также очевидно, что анализ «Мазера» более информативен и что на его основе всегда можно построить анализ «Фишера». Однако обратное преобразование невозможно, поскольку информация о cov- _{рекламе} будет отсутствовать.

Дисперсия и генотипическая дисперсия

В разделе, посвященном генетическому дрейфу, и в других разделах, посвященных инбридингу, основным результатом выборки частот аллелей стал разброс средних значений потомства. Этот набор средних имеет собственное среднее значение, а также дисперсию: межстрочную дисперсию . (Это вариация самого признака, а не частот аллелей .) По мере дальнейшего развития дисперсии в последующих поколениях можно ожидать, что эта межлинейная дисперсия будет увеличиваться. И наоборот, по мере повышения гомозиготности можно ожидать, что внутрилинейная дисперсия уменьшится. Поэтому возникает вопрос, меняется ли общая дисперсия, и если да, то в каком направлении. На сегодняшний день эти вопросы были представлены с точки зрения генного (σ ² _A ) и квазидоминирование (σ ² _D ) дисперсии, а не компоненты генной модели. Это будет сделано и здесь.

Ключевое уравнение обзора принадлежит Сьюэллу Райту: и представляет собой схему инбредной генотипической дисперсии, основанную на средневзвешенном значении ее крайних значений , причем веса квадратичны по отношению к коэффициенту инбридинга. ${\textstyle f}$. Это уравнение:

$$\sigma _{G_{f}}^{2}=\left(1-f\right)\sigma _{G_{0}}^{2}+f\ \sigma _{G_{1}}^{2}+f\left(1-f\right)\left[G_{0}-G_{1}\right]^{2}$$

где ${\textstyle f}$ коэффициент инбридинга, ${\textstyle \sigma _{G_{0}}^{2}}$ это генотипическая дисперсия е=0 , ${\textstyle \sigma _{G_{1}}^{2}}$ - генотипическая дисперсия при f=1 , ${\textstyle G_{0}}$ среднее значение численности населения при f=0 , и ${\textstyle G_{1}}$ — среднее значение численности населения при f=1 .

The ${\textstyle \left(1-f\right)}$ Компонент [в приведенном выше уравнении] характеризует уменьшение дисперсии внутри линий потомства. ${\textstyle f}$ Компонент направлен на увеличение вариативности между линиями потомства. Наконец, ${\textstyle f\left(1-f\right)}$ Компонент виден (в следующей строке), чтобы устранить дисперсию квазидоминирования . Эти компоненты можно расширить дальше, тем самым раскрывая дополнительную информацию. Таким образом:-

$$\sigma _{G_{f}}^{2}=\left(1-f\right)\left[\sigma _{A_{0}}^{2}+\sigma _{D_{0}}^{2}\right]+f\ \left(4pq\ a^{2}\right)+f\ \left(1-f\right)\left[2pq\ d\right]^{2}$$

Во-первых, σ ² _G(0) [в приведенном выше уравнении] был расширен, чтобы показать два его подкомпонента [см. раздел «Генотипическая дисперсия»]. Далее, σ ² _G(1) преобразован в 4pqa. ² , и выводится в следующем разделе. Замена третьего компонента представляет собой разницу между двумя «инбридинговыми крайностями» среднего значения популяции [см. раздел «Среднее значение популяции»].

Дисперсия и компоненты генотипической дисперсии

Подводя итог: внутрилинейные компоненты ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ и ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$; и межстрочные компоненты ${\textstyle 2f\ \sigma _{a_{0}}^{2}}$ и ${\textstyle \left(f-f^{2}\right)\sigma _{D_{0}}^{2}}$.

Развитие дисперсии дисперсии

Перестановка дает следующее: $${\begin{aligned}\sigma _{A_{inbred}}^{2}&=\left(1-f\right)\sigma _{A_{0}}^{2}+2f\sigma _{a_{0}}^{2}\\&=\left(1+f\right)\sigma _{A_{f}}^{2}\end{aligned}}$$ Версия в последней строке обсуждается далее в следующем разделе.

Сходным образом, $${\begin{aligned}\sigma _{D_{inbred}}^{2}&=\left(1-f\right)\sigma _{D_{0}}^{2}+\left(f-f^{2}\right)\sigma _{D_{0}}^{2}\\&=\left(1-f^{2}\right)\sigma _{D_{0}}^{2}\end{aligned}}$$

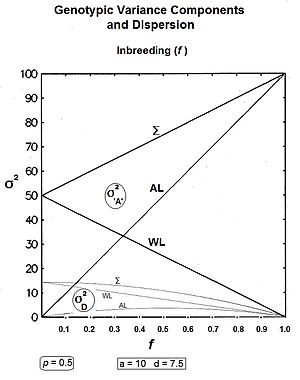
Графики слева показывают эти три генные дисперсии вместе с тремя дисперсиями квазидоминирования для всех значений f для p = 0,5 (при котором дисперсия квазидоминирования максимальна). Графики справа показывают разделы генотипической дисперсии (представляющие собой суммы соответствующих разделов генного и квазидоминирования ), изменяющиеся в течение десяти поколений на примере f = 0,10 .

Отвечая, во-первых, на вопросы, поставленные в начале об общих дисперсиях ( Σ на графиках): генная дисперсия растет линейно с коэффициентом инбридинга , достигая максимума в два раза по сравнению с начальным уровнем. Дисперсия квазидоминирования снижается со скоростью (1 − f ² ), пока не закончится на нуле. При низких уровнях f снижение происходит очень постепенно, но оно ускоряется при более высоких уровнях f .

Во-вторых, обратите внимание на другие тенденции. Вероятно, интуитивно понятно, что внутрилинейные дисперсии снижаются до нуля при продолжении инбридинга, и это действительно так (обе с одинаковой линейной скоростью (1-f) ). Вариации между линиями увеличиваются с инбридингом до f = 0,5 , генная дисперсия со скоростью 2f и дисперсия квазидоминирования со скоростью (f - f ² ) . Однако при f > 0,5 тенденции меняются. между линиями Генная дисперсия продолжает линейно увеличиваться до тех пор, пока не станет равной общей генетической дисперсии . Но среди линий дисперсия квазидоминирования теперь снижается до нуля , потому что (f − f ² ) также снижается при f > 0,5 .

Вывод σ ² _Г(1)

Напомним, что когда f=1 , гетерозиготность равна нулю, внутрилинейная дисперсия равна нулю, и вся генотипическая дисперсия, таким образом, является межлинейной дисперсией и лишена дисперсии доминирования. Другими словами, σ ² _G(1) — это дисперсия среди средних значений полностью инбредных линий. Вспомните далее [из раздела «Среднее значение после самооплодотворения», что такими средними (фактически G ₁ ) являются G = a(pq) . Подстановка (1-q) на p дает G ₁ = a (1 - 2q) = a - 2aq . Следовательно, σ ² _G(1) — это σ ² _(a-2aq) на самом деле. Теперь, в общем, дисперсия разности (xy) равна [ σ ² _х + р ² _y - 2 cov _xy ] . Следовательно, σ ² _G(1) = [ п ² _а + р ² _2aq - 2 cov _{(a, 2aq)} ] . Но a аллеля ( эффект ) и q аллеля ( частота ) независимы , поэтому эта ковариация равна нулю. Более того, a является константой от одной строки к другой, поэтому σ ² _а также равно нулю. Кроме того, 2a — еще одна константа (k), поэтому σ ² _2aq имеет тип σ ² _к Х. В общем случае дисперсия σ ² _{k X} равен k ² п ² _Х. ​ Если сложить все это вместе, то окажется, что σ ² _(а-2aq) = (2а) ² п ² _q . Напомним [из раздела «Продолжение генетического дрейфа»], что σ ² _q знак равно pq ж . При f=1 здесь, в рамках данного вывода, это становится pq 1 (то есть pq ), и оно заменяется на предыдущее.

Конечный результат: σ ² _Г(1) = п ² _(а-2aq) = 4а ² pq = 2(2pq а ² ) = 2 п ² _а .

Отсюда сразу следует, что f σ ² _Г(1) = ж 2 п ² _а . [Последнее f происходит из исходного уравнения Сьюэлла-Райта : это не то f, которое только что было установлено равным «1» в выводе, заключенном двумя строками выше.]

Общая дисперсная генная дисперсия – σ ² _A(f) и β _f

В предыдущих разделах было обнаружено, что внутрилинейная генная вариабельность основана на вызванной заменами генной вариативности, ( σ ² _A ) — но между линиями генная вариабельность основана на модели гена аллельной вариабельности ( σ ² _а ) . Эти два вида нельзя просто сложить, чтобы получить общую генную вариативность . Одним из подходов, позволяющих избежать этой проблемы, было повторное рассмотрение вывода среднего эффекта замены аллеля и построение версии ( β _f ) , которая включает эффекты дисперсии. Кроу и Кимура добились этого. с использованием эффектов перецентрированной аллели ( a•, d•, (-a)• ), обсуждавшихся ранее [«Переопределение эффектов генов»]. Однако впоследствии было обнаружено, что это несколько недооценивает общую генетическую дисперсию , и новый вывод, основанный на дисперсии, привел к уточненной версии.

версия Уточненная : β _f = { a ² + [(1− f ) / (1 + f )] 2(q − p ) ad + [(1- f ) / (1 + f )] (q − p ) ² д ² } ^(1/2)

Следовательно, σ ² _A(f) = (1 + f ) 2pq β _f ² теперь согласуется с [ (1-f) σ ² _А(0) + 2f р ² _a(0) ] точно.

Общие и разделенные дисперсные дисперсии квазидоминирования

Общая генетическая вариативность сама по себе представляет интерес. Но до уточнений Гордона у него было и еще одно важное применение. Оценок «рассредоточенного» квазидоминирования не существовало. Это было оценено как разница между инбредной генотипической дисперсией Сьюэлла Райта. и общая «рассеянная» генетическая вариативность [см. предыдущий подраздел]. Однако возникла аномалия, поскольку общая дисперсия квазидоминирования, по-видимому, увеличивалась на ранних этапах инбридинга, несмотря на снижение гетерозиготности.

Уточнения в предыдущем подразделе исправили эту аномалию. В то же время было получено прямое решение для полной дисперсии квазидоминирования , что позволило избежать необходимости использования метода «вычитания», как в предыдущие разы. прямые решения для межлинейного и внутристрочного распределения дисперсии квазидоминирования Кроме того, впервые были получены . [Они представлены в разделе «Дисперсия и генотипическая дисперсия».]

Экологическая изменчивость

Экологическая изменчивость — это фенотипическая изменчивость, которую нельзя приписать генетике. Это звучит просто, но экспериментальный план, необходимый для разделения этих двух явлений, требует очень тщательного планирования. Даже «внешнюю» среду можно разделить на пространственную и временную составляющие («Места» и «Годы»); или на такие разделы, как «помет» или «семья» и «культура» или «история». Эти компоненты во многом зависят от фактической экспериментальной модели, использованной для проведения исследования. Такие вопросы очень важны при проведении самих исследований, но в этой статье о количественной генетике этого обзора может быть достаточно.

Однако это подходящее место для подведения итогов:

Фенотипическая дисперсия = генотипическая дисперсия + дисперсия окружающей среды + взаимодействие генотипа и окружающей среды + экспериментальная дисперсия «ошибок».

т. е. σ ² _П = п ² _Г + р ² _Э + р ² _ГЭ + р ²

или σ ² _П = п ² _А + р ² _Д + р ² _я + п ² _Э + р ² _ГЭ + р ²

после разделения генотипической дисперсии (G) на составляющие дисперсии «генная» (А), «квазидоминантная» (D) и «эпистатическая» (I).

Отклонения от окружающей среды появятся в других разделах, таких как «Наследственность» и «Коррелированные атрибуты».

Наследственность и повторяемость

Наследуемость σ признака — это доля общей (фенотипической) дисперсии ( ² _P ), что связано с генетической изменчивостью, будь то полная генотипическая изменчивость или какой-то ее компонент. Он количественно определяет степень, в которой фенотипическая изменчивость обусловлена ​​генетикой: но точное значение зависит от того, какой раздел генетической вариативности используется в числителе пропорции. Исследовательские оценки наследственности имеют стандартные ошибки, как и вся оценочная статистика.

Где дисперсия числителя представляет собой всю генотипическую дисперсию ( σ ² _G ), наследственность известна как наследственность «широкого смысла» ( H ² ). Он количественно определяет степень, в которой изменчивость признака определяется генетикой в ​​целом. $${\begin{aligned}H^{2}&={\frac {\sigma _{G}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\sigma _{A}^{2}+\sigma _{D}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\left[\sigma _{a}^{2}+\sigma _{d}^{2}+cov_{ad}\right]+\sigma _{D}^{2}}{\sigma _{P}^{2}}}\end{aligned}}$$ [См. раздел «Генотипическая дисперсия».]

Если бы только генная дисперсия ( σ ² _A ) используется в числителе, то наследуемость можно назвать «узким смыслом» (h ² ). Он количественно определяет степень, в которой фенотипическая дисперсия определяется дисперсией ожиданий замещения Фишера . $${\begin{aligned}h^{2}&={\frac {\sigma _{A}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\sigma _{a}^{2}+\sigma _{d}^{2}+cov_{ad}}{\sigma _{P}^{2}}}\end{aligned}}$$Фишер предположил, что эта наследственность в узком смысле может быть уместна при рассмотрении результатов естественного отбора, уделяя особое внимание способности к изменению, то есть «адаптации». Он предложил это в отношении количественной оценки дарвиновской эволюции.

Вспоминая, что аллельная дисперсия ( σ ² _a ) и дисперсия доминирования ( σ ² _d ) являются эвгенетическими компонентами генной модели (см. раздел «Генотипическая дисперсия») и что σ ² _D ( отклонения замещения или «квазидоминантности» дисперсия ) и cov _ad обусловлены переходом от средней точки гомозиготы ( mp ) к популяционному среднему значению ( G ), можно видеть, что реальные значения этих наследственностей неясны. Наследственность ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ и ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ имеют однозначное значение.

Наследственность в узком смысле использовалась также для прогнозирования результатов искусственного отбора . Однако в последнем случае наследственность в широком смысле может быть более подходящей, поскольку изменяется весь атрибут, а не только адаптивная способность. Как правило, прогресс от отбора происходит тем быстрее, чем выше наследственность. [См. раздел «Отбор».] У животных наследственность репродуктивных признаков обычно низкая, тогда как наследственность устойчивости к болезням и продуктивности от умеренно низкой до умеренной, а наследственность строения тела высокая.

Повторяемость (r ² ) — это доля фенотипической дисперсии, обусловленная различиями в повторных измерениях одного и того же субъекта, возникающими из более поздних записей. Его используют, в частности, для долгоживущих видов. Это значение можно определить только для признаков, которые проявляются несколько раз в течение жизни организма, таких как масса тела взрослой особи, скорость метаболизма или размер помета. Например, индивидуальная масса тела при рождении не будет иметь значения повторяемости, но будет иметь значение наследственности. Обычно, но не всегда, повторяемость указывает на верхний уровень наследуемости.

р ² = (с ² _Г +С ² _ПЭ )/с ² _П

где с ² _PE = взаимодействие фенотипа и окружающей среды = повторяемость.

Однако вышеупомянутая концепция повторяемости проблематична для признаков, которые обязательно сильно изменяются между измерениями. Например, у многих организмов масса тела значительно увеличивается в период между рождением и взрослением. Тем не менее, в пределах данного возрастного диапазона (или этапа жизненного цикла) можно проводить повторные измерения, и на этом этапе повторяемость будет иметь значение.

Отношение

Связь между коэффициентами инбридинга и родства.

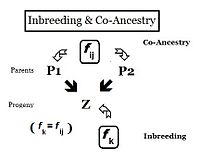
С точки зрения наследственности, родственники — это особи, унаследовавшие гены от одного или нескольких общих предков. Следовательно, их «родство» можно оценить количественно, исходя из вероятности того, что каждый из них унаследовал копию аллели от общего предка. В предыдущих разделах коэффициент инбридинга определялся как «вероятность того, что две одинаковые аллели ( А и А или а и а ) имеют общее происхождение» — или, более формально, «Вероятность того, что две гомологичные аллели являются автозиготными». " Раньше упор делался на вероятность наличия у человека двух таких аллелей, и коэффициент составлялся соответствующим образом. Однако очевидно, что эта вероятность аутозиготности для особи должна также быть вероятностью того, что каждый из двух ее родителей имел этот автозиготный аллель. В этой перефокусированной форме вероятность называется коэффициентом совместного происхождения для двух людей i и j ( f _ij ). В этой форме его можно использовать для количественной оценки отношений между двумя людьми, а также его можно назвать коэффициент родства или коэффициент кровного родства .

Родословный анализ

Иллюстративная родословная.

Родословные — это диаграммы семейных связей между людьми и их предками и, возможно, между другими членами группы, которые разделяют с ними генетическое наследование. Это карты отношений. Таким образом, можно проанализировать родословную, чтобы выявить коэффициенты инбридинга и родства. Такие родословные на самом деле являются неформальным изображением диаграмм путей , используемых в анализе путей , который был изобретен Сьюэллом Райтом, когда он формулировал свои исследования по инбридингу. Используя соседнюю диаграмму, вероятность того, что особи «B» и «C» получили автозиготные аллели от предка «A», равна 1/2 (один из двух диплоидных аллелей). Это инбридинг «de novo» ( Δf _Ped ) на данном этапе. Однако другой аллель мог иметь аутозиготность «переноса» от предыдущих поколений, поэтому вероятность этого равна ( комплементация de novo , умноженная на инбридинг предка A ), то есть (1 − Δf _Ped ) f _A = ( 1/2) _А. ж Следовательно, общая вероятность автозиготности у B и C после бифуркации родословной равна сумме этих двух компонентов, а именно (1/2) + (1/2)f _A = (1/2) ( 1+f _А ) . Это можно рассматривать как вероятность того, что две случайные гаметы предка А несут автозиготные аллели, и в этом контексте называется коэффициентом происхождения ( f _AA ). Оно часто появляется в следующих абзацах.

Следуя по пути «B», вероятность того, что какой-либо автозиготный аллель «передастся» каждому последующему родителю, снова равна (1/2) на каждом этапе (включая последний «целевой» X ). Таким образом, общая вероятность передачи по «пути B» равна (1/2). ³ . Степень, до которой возводится (1/2), можно рассматривать как «количество промежуточных звеньев на пути между A и X », n _B = 3 . Аналогично, для «пути C» n _C = 2 , а «вероятность передачи» равна (1/2). ² . Таким образом, совокупная вероятность автозиготного переноса от A к X равна [ f _AA (1/2) ^{(н _Б )} (1/2) ^{(н _С )} ] . Вспоминая, что f _AA = (1/2) (1+f _A ) , f _X = f _PQ = (1/2) ^{(п _Б + н _С + 1)} (1 + ж _А ) . В этом примере, если предположить, что f ₌ 0, f _X = 0,0156 (округлено) = f _PQ , это одна мера «связности» между P и Q. A

В этом разделе степени ( 1/2 ) использовались для представления «вероятности автозиготности». Позже этот же метод будет использован для представления пропорций наследственных генофондов, наследуемых по родословной [раздел «Родство между родственниками»].

Правила перекрестного умножения.

Правила перекрестного умножения

В следующих разделах, посвященных скрещиваниям и подобным темам, будет полезен ряд «правил усреднения». Они вытекают из анализа пути . Правила показывают, что любой коэффициент совместного происхождения может быть получен как среднее значение перекрестного совместного происхождения между соответствующими комбинациями дедушек и родителей. Таким образом, ссылаясь на соседнюю диаграмму, перекрестный множитель 1 означает, что f _PQ = среднее значение ( f _AC , f _AD , f _BC , f _BD ) = (1/4) [f _AC + f _AD + f _BC + f _BD ] знак равно ж _Y . Аналогичным образом перекрестный множитель 2 утверждает, что f _PC = (1/2) [f _AC + f _BC ] — тогда как перекрестный множитель 3 утверждает, что f _PD = (1/2) [ f _AD + f _BD ] . Возвращаясь к первому множителю, теперь можно увидеть, что он также равен f _PQ = (1/2) [ f _PC + f _PD ] , который после замены множителей 2 и 3 возобновляет свою первоначальную форму.

В дальнейшем поколение прародителей обозначается как (t-2) , родительское поколение — как (t-1) , а «целевое» поколение — как t .

Полное сибс-кроссинг (FS)

Инбридинг в родственных отношениях

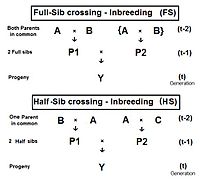
Диаграмма справа показывает, что полное скрещивание сибсов является прямым применением перекрестного множителя 1 с небольшой модификацией, которую повторяют родители A и B (вместо C и D ), чтобы указать, что у особей P1 и P2 есть оба родителя . в общем, то есть они полные братья и сестры . Особь Y является результатом скрещивания двух полных братьев и сестер. Следовательно, f _Y = f _P1,P2 = (1/4) [ f _AA + 2 f _AB + f _BB ] . Напомним, что f _AA и f _BB были определены ранее (при анализе родословной) как коэффициенты происхождения , равные (1/2)[1+f _A ] и (1/2)[1+f _B ] соответственно, в настоящем контекст. Помните, что в этом облике предки A и B представляют поколение (t-2) . Таким образом, если предположить, что в любом поколении все уровни инбридинга одинаковы, этих двух коэффициентов происхождения каждый из представляет собой (1/2) [1 + f _(t-2) ] .

Инбридинг от скрещивания полнородных и полусибсов, а также от самоопыления.

Теперь рассмотрим f _AB . Напомним, что это тоже f _P1 или f _P2 и поэтому представляет их поколение — f _(t-1) . Сложив все это вместе, f _t = (1/4) [ 2 f _AA + 2 f _AB ] = (1/4) [ 1 + f _(t-2) + 2 f _(t-1) ] . Это коэффициент инбридинга для скрещивания Full-Sib . График слева показывает скорость этого инбридинга в течение двадцати повторяющихся поколений. «Повторение» означает, что потомство после цикла t становится родителями-скрещивающимися, которые порождают цикл ( t+1 ), и так далее последовательно. На графиках также для сравнения показан инбридинг при случайном оплодотворении 2N=20 . Напомним, что этот коэффициент инбридинга для потомства Y также является коэффициентом совместного происхождения для его родителей, а также является мерой родства двух братьев и сестер Fill .

Полуродственное скрещивание (HS)

Вывод скрещивания полуродственных братьев происходит немного иначе, чем для полных сибсов. На соседней диаграмме два сводных брата в поколении (t-1) имеют только одного общего родителя — родителя «А» в поколении (t-2). Перекрестный множитель 1 используется снова, что дает f _Y = f _(P1,P2) = (1/4) [ f _AA + f _AC + f _BA + f _BC ] . На этот раз существует только один коэффициент отцовства , но три коэффициента совместного происхождения на уровне (t-2) (один из них — f _{BC —} является «пустышкой» и не представляет реального человека на уровне (t-1) поколение). Как и раньше, коэффициент происхождения равен (1/2)[1+f _A ] , и каждый из трех родственников представляет f _(t-1) . Вспоминая, что f _A представляет собой f _(t-2) , окончательный сбор и упрощение терминов дает f _Y = f _t = (1/8) [ 1 + f _(t-2) + 6 f _(t-1) ] . Графики слева включают инбридинг полусибса (HS) в течение двадцати последовательных поколений.

Самооплодотворение, инбридинг

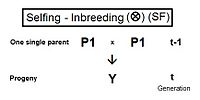
Как и раньше, это также количественно определяет родство двух полусибсов в поколении (t-1) в альтернативной форме f _{(P1, P2)} .

Самооплодотворение (SF)

Справа приведена родословная схема для самоопыления. Это настолько просто, что не требует каких-либо правил перекрестного умножения. Он использует только базовое сопоставление коэффициента инбридинга и его альтернативы коэффициента родства ; с последующим признанием того, что в данном случае последний также является коэффициентом происхождения . Таким образом, f _Y = f _{(P1, P1)} = f _t = (1/2) [ 1 + f _(t-1) ] . Это самый быстрый темп инбридинга из всех типов, как видно на графиках выше. Кривая самоопыления, по сути, представляет собой график коэффициента происхождения .

Переезды кузенов

Анализ родословной двоюродных братьев и сестер

Они получены методами, аналогичными методам для братьев и сестер. Как и раньше, совместного происхождения с точки зрения коэффициент инбридинга обеспечивает меру «родства» между родителями P1 и P2 в этих выражениях кузена.

Родословная двоюродных братьев и сестер (FC) указана справа. Простое уравнение: f _Y = f _t = f _P1,P2 = (1/4) [ f _1D + f ₁₂ + f _CD + f _C2 ] . После замены соответствующими коэффициентами инбридинга, сбора терминов и упрощения это становится f _t = (1/4) [ 3 f _(t-1) + (1/4) [2 f _(t-2) + f _{(t- 3)} + 1 ]] , версия для итерации, полезная для наблюдения за общей закономерностью и для компьютерного программирования. «Окончательная» версия — f _t = (1/16) [ 12 f _(t-1) + 2 f _(t-2) + f _(t-3) + 1 ] .

Анализ родословной троюродных братьев и сестер

Родословная троюродных братьев и сестер (SC) находится слева. Родители в родословной, не относящиеся к общему Предку, обозначаются цифрами вместо букв. Здесь простое уравнение имеет вид f _Y = f _t = f _P1,P2 = (1/4) [ f _3F + f ₃₄ + f _EF + f _E4 ] . После работы с соответствующей алгеброй это становится f _t = (1/4) [ 3 f _(t-1) + (1/4) [3 f _(t-2) + (1/4) [2 f _{(t -3)} + f _(t-4) + 1 ]]] , что является итерационной версией. «Окончательная» версия — f _t = (1/64) [ 48 f _(t-1) + 12 f _(t-2) + 2 f _(t-3) + f _(t-4) + 1 ] .

Инбридинг от нескольких уровней двоюродного скрещивания.

Чтобы визуализировать закономерность в уравнениях полного кузена , начните серию с полного уравнения sib , переписанного в итерационной форме: f _t = (1/4)[2 f _(t-1) + f _(t-2) + 1 ] . Обратите внимание, что это «основной план» последнего члена в каждой из итеративных форм двоюродного брата: с той небольшой разницей, что индексы генерации увеличиваются на «1» на каждом «уровне» двоюродного брата. Теперь определите уровень двоюродного брата как k = 1 (для двоюродных братьев и сестер), = 2 (для троюродных братьев и сестер), = 3 (для троюродных братьев и сестер) и т. д. и т. п.; и = 0 (для полных сибсов, которые являются «двоюродными братьями нулевого уровня»). Последний член теперь можно записать как: (1/4) [ 2 f _(t-(1+k)) + f _(t-(2+k)) + 1] . Перед этим последним членом складываются один или несколько приращений итерации в форме (1/4) [ 3 f _(tj) + ... , где j - индекс итерации и принимает значения от 1 ... k на протяжении последовательных итерации по мере необходимости. Собрав все это вместе, можно получить общую формулу для всех возможных уровней полнородных кузенов , включая полных сибсов . Для k -го уровня полных кузенов f{k} _t = Ιter _{j = 1} ^к { (1/4) [ 3 f _(tj) + } _j + (1/4) [ 2 f _(t-(1+k)) + f _(t-(2+k)) + 1] . В начале итерации всем f _{(t- x )} присваивается значение «0», и каждое значение заменяется по мере его вычисления в ходе поколений. Графики справа показывают последовательное инбридинг для нескольких уровней полных кузенов.

Анализ родословной сводных двоюродных братьев и сестер

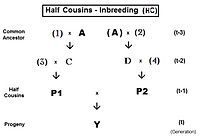
У двоюродных братьев и сестер (FHC) родословная слева. Обратите внимание, что есть только один общий предок (человек А ). Также, что касается троюродных братьев и сестер , то родители, не связанные с общим предком, обозначаются цифрами. Здесь простое уравнение имеет вид f _Y = f _t = f _P1,P2 = (1/4) [ f _3D + f ₃₄ + f _CD + f _C4 ] . После работы с соответствующей алгеброй это становится f _t = (1/4) [ 3 f _(t-1) + (1/8) [6 f _(t-2) + f _(t-3) + 1 ]] , что является версией итерации. «Окончательная» версия — f _t = (1/32) [ 24 f _(t-1) + 6 f _(t-2) + f _(t-3) + 1 ] . Алгоритм итерации аналогичен алгоритму для полных кузенов , за исключением того, что последний член равен (1/8) [ 6 f _(t-(1+k)) + f _(t-(2+k)) + 1 ] . Обратите внимание, что этот последний член в основном аналогичен уравнению полуродственного брата, параллельно модели для полных кузенов и полных братьев и сестёр. Другими словами, сводные братья и сестры являются сводными двоюродными братьями «нулевого уровня».

Существует тенденция рассматривать скрещивание кузенов с точки зрения, ориентированной на человека, возможно, из-за широкого интереса к генеалогии. Использование родословных для установления инбридинга, возможно, усиливает эту точку зрения на «семейную историю». Однако такие виды скрещивания происходят и в естественных популяциях, особенно в тех, которые ведут оседлый образ жизни или имеют «зону размножения», которую они повторно посещают из сезона в сезон. Группа потомства гарема с доминирующим самцом, например, может содержать элементы скрещивания братьев и сестер, кузена и обратного скрещивания, а также генетического дрейфа, особенно «островного» типа. В дополнение к этому, случайное «ауткросс» добавляет в смесь элемент гибридизации. Это не панмиксия.

Обратное скрещивание (BC)

Анализ родословной: обратное скрещивание

Бэккроссинг: базовые уровни инбридинга

После гибридизации между A и R F1 ) с (индивид B ) скрещивается обратно ( BC1 исходным родителем ( R ) для получения поколения BC1 (индивид C ). [Обычно используют один и тот же ярлык для акта обратного скрещивания и для поколения, произведенного в результате него. Акт обратного скрещивания выделен курсивом . ] Родитель R — повторяющийся родительский элемент. Изображены два последовательных обратных скрещивания, причем отдельный D представляет собой поколение BC2 . Как указано, этим поколениям также были присвоены t- индексы. Как и раньше, f _D = f _t = f _CR = (1/2) [ f _RB + f _RR ] с использованием ранее заданного перекрестного множителя 2 . Только что определенный f ( _RB — это тот, который включает генерацию t-1) с (t-2) . Однако существует еще один такой f _RB, полностью содержащийся в поколении (t-2) , и именно он используется сейчас: как совместное происхождение индивидуума родителей C в поколении (t-1) . По существу, это также коэффициент инбридинга C и , следовательно, f _(t-1) . Оставшийся f _RR представляет собой коэффициент происхождения рекуррентного родителя. , а также (1/2) [1 + f _R ] . Сложим все это вместе: f _t = (1/2) [ (1/2) [ 1 + f _R ] + f _(t-1) ] = (1/4) [ 1 + f _R + 2 f _{(t- 1)} ] . Графики справа иллюстрируют инбридинг обратного скрещивания более двадцати обратных скрещиваний для трех различных уровней (фиксированного) инбридинга у рекуррентного родителя.

Эта процедура обычно используется в программах по разведению животных и растений. Часто после создания гибрида (особенно если особи недолговечны) рекуррентному родителю требуется отдельное «линейное разведение» для его поддержания в качестве будущего рекуррентного родителя при обратном скрещивании. Это поддержание может осуществляться путем самоопыления, скрещивания полных или полусибсов или за счет ограниченных случайно оплодотворенных популяций, в зависимости от репродуктивных возможностей вида. Конечно, это постепенное повышение f _R переносится и на f _t обратного скрещивания. В результате кривая поднимается к асимптотам более плавно, чем показано на настоящих графиках, поскольку f _R не находится на фиксированном уровне с самого начала.

Вклад наследственных генофондов

В разделе «Анализ родословной» ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ использовался для представления вероятностей автозиготного происхождения аллелей в течение n поколений по ветвям родословной. Эта формула возникла из-за правил, налагаемых половым размножением: (i) два родителя вносят практически равные доли аутосомных генов и (ii) последовательное разбавление для каждого поколения между зиготой и «фокусным» уровнем происхождения. Эти же правила применимы и к любой другой точке зрения на происхождение в двуполой репродуктивной системе. Одним из них является доля любого наследственного генофонда (также известного как «зародышевая плазма»), которая содержится в генотипе любой зиготы.

Следовательно, доля предкового генофонда в генотипе равна: $$\gamma _{n}=\left({\frac {1}{2}}\right)^{n}$$ где n = количество половых поколений между зиготой и фокусным предком.

Например, каждый родитель определяет генофонд, способствующий ${\textstyle \left({\tfrac {1}{2}}\right)^{1}}$ своему потомству; в то время как каждый прадедушка и прадедушка вносят свой вклад ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ своему праправнуку.

Общий генофонд зиготы ( Γ ), конечно, представляет собой сумму полового вклада в ее происхождение.

$${\begin{aligned}\Gamma &=\sum _{n=1}^{2^{n}}{\gamma _{n}}\\&=\sum _{n=1}^{2^{n}}{\left({\frac {1}{2}}\right)^{n}}\end{aligned}}$$

Отношения через наследственные генофонды

Лица, произошедшие от общего предкового генофонда, очевидно, связаны между собой. Это не означает, что они идентичны по своим генам (аллелям), поскольку на каждом уровне предка при образовании гамет происходит сегрегация и сортировка. Но они произошли из того же пула аллелей, доступных для этих мейозов и последующих оплодотворений. [Эта идея впервые была встречена в разделах, посвященных анализу родословной и взаимоотношениям.] Таким образом, вклад генофонда [см. раздел выше] их ближайшего общего предкового генофонда ( предкового узла ) может быть использован для определения их родства. Это приводит к интуитивному определению отношений, которое хорошо согласуется со знакомыми представлениями о «родстве», встречающимися в семейной истории; и позволяет сравнивать «степень родства» для сложных моделей отношений, возникающих из такой генеалогии.

Единственные необходимые модификации (по очереди для каждого человека) находятся в Γ и связаны с переходом к «общему общему предку», а не к «индивидуальному общему происхождению». Для этого определим Р (вместо Г ); m = количество общих предков в узле (т.е. m = только 1 или 2); и «индивидуальный индекс» k . Таким образом:

$${\begin{aligned}\mathrm {P} _{k}&=\sum _{m=1}^{1,2}{\gamma _{n}}\\&=\sum _{m=1}^{1,2}{\left({\frac {1}{2}}\right)^{n}}\end{aligned}}$$

где, как и раньше, n = количество половых поколений между особью и предковым узлом.

Примером могут служить двое двоюродных братьев и сестер. Их ближайшим общим предковым узлом являются их бабушка и дедушка, которые дали начало двум их родным братьям и сестрам, и у них обоих есть общие дедушка и бабушка. [См. предыдущую родословную.] В этом случае m=2 и n=2 , поэтому для каждого из них

$${\begin{aligned}\mathrm {P} _{k}&=\sum _{m=1}^{2}{\gamma _{2}}\\&=\sum _{m=1}^{2}{\left({\frac {1}{2}}\right)^{2}}\\&={\frac {1}{2}}\end{aligned}}$$

В этом простом случае каждый двоюродный брат имеет численно одно и то же Р.

Второй пример может быть между двумя полными кузенами, но один ( k=1 ) имеет три поколения до исходного узла (n=3), а другой ( k=2 ) только два (n=2) [т.е. второе и отношения двоюродного брата]. Для обоих m=2 (они полные родственники).

$${\begin{aligned}\mathrm {P} _{1}&=\sum _{m=1}^{2}{\gamma _{3}}\\&=\sum _{m=1}^{2}{\left({\frac {1}{2}}\right)^{3}}\\&={\frac {1}{4}}\end{aligned}}$$

и

$${\begin{aligned}\mathrm {P} _{2}&=\sum _{m=1}^{2}{\gamma _{2}}\\&=\sum _{m=1}^{2}{\left({\frac {1}{2}}\right)^{2}}\\&={\frac {1}{2}}\end{aligned}}$$

Обратите внимание, что у каждого двоюродного брата есть разные Ρ _k .

GRC – коэффициент родства генофонда.

При любой попарной оценке отношений для каждой особи имеется один Ρ _k : остается их усреднить, чтобы объединить в единый «Коэффициент связи». Поскольку каждое Р представляет собой часть общего генофонда , подходящим средним значением для них является среднее геометрическое. Это среднее значение и есть их коэффициент родства генофонда — «GRC».

Для первого примера (два полных двоюродных брата) их GRC = 0,5; для второго случая (полный двоюродный и троюродный брат) их GRC = 0,3536.

Все эти отношения (GRC) являются приложениями путевого анализа. Ниже приводится краткое описание некоторых уровней взаимоотношений (GRC).

ГРЦ	Примеры отношений
1.00	полные братья и сестры
0.7071	Родитель ↔ Потомство; Дядя/тетя ↔ Племянник/Племянница
0.5	полные двоюродные братья; наполовину сибсы; великий родитель ↔ великий потомок
0.3536	полный Кузенс Первый ↔ Второй; полная версия «Двоюродные братья» {1 удалить}
0.25	полные троюродные братья; наполовину двоюродные братья и сестры; полная версия «Двоюродные братья» {2 удалений}
0.1768	полная версия «Двоюродный брат» {3 удаления}; полная Троюродные братья {1 удалить}
0.125	полные троюродные братья и сестры; половина троюродных братьев и сестер; полностью Двоюродные братья и сестры {4 удаления}
0.0884	полные двоюродные братья {5 удалений}; половина троюродных братьев и сестер {1 удалить}
0.0625	полные четвертые кузены; половина троюродных братьев и сестер

Сходство между родственниками

Они, как и генотипические вариации, могут быть получены либо с помощью подхода генной модели («Мазер»), либо подхода аллель-замены («Фишер»). Здесь каждый метод демонстрируется для альтернативных случаев.

Ковариация родителей и потомков

Их можно рассматривать либо как ковариацию между любым потомком и любым из его родителей ( PO ), либо как ковариацию между любым потомком и значением «промежуточного родителя» обоих его родителей ( MPO ).

Один родитель и потомство (PO)

Это можно получить как сумму перекрестных произведений между эффектами родительских генов и половиной ожиданий потомства с использованием подхода аллель-замены. Половина ожидаемого потомства объясняется тем фактом, что только один из двух родителей рассматривается . Таким образом, соответствующие эффекты родительских генов представляют собой переопределенные генные эффекты второй стадии, используемые для определения генотипических отклонений ранее, то есть: a″ = 2q(a − qd) и d″ = (qp)a + 2pqd , а также (-a )″ = -2p(a + pd) [см. раздел «Переопределение эффектов генов»]. Аналогичным образом, соответствующие эффекты потомства для ожиданий замены аллелей составляют половину значений более раннего разведения , причем последнее составляет: a _AA = 2qa , a _Aa = (qp)a а также aa _, = -2pa [см. раздел, посвященный «Замена генотипа – ожидания и отклонения».

Поскольку все эти эффекты уже определены как отклонения от среднего генотипического значения, сумма перекрестного произведения с использованием { частота генотипа * эффект родительского гена * значение полуразведения } немедленно обеспечивает ковариацию ожиданий замены аллелей между любым одним родителем. и его потомство. После тщательного сбора терминов и упрощения получается cov(PO) _A = pqa. ² = ⁠ 1/2 ​ ⁠ с ​ ² _А. ​

К сожалению, аллель-замещения-отклонения обычно не замечают, но они тем не менее не «перестали существовать»! Напомним, что эти отклонения составляют: d _AA = -2q ² d и d _Aa = 2pq d , а также d _aa = -2p ² d [см. раздел «Замена генотипа – ожидания и отклонения»]. Следовательно, сумма перекрестного произведения с использованием { частота генотипа * эффект родительского гена * отклонения половинных замен } также немедленно обеспечивает ковариацию отклонений аллель-замены между любым одним родителем и его потомством. Еще раз, после тщательного сбора терминов и упрощения, это становится cov(PO) _D = 2p. ² д ² д ² = ⁠ 1/2 ​ ⁠ с ​ ² _Д. ​

Отсюда следует, что: cov(PO) = cov(PO) _A + cov(PO) _D = ⁠ 1/2 ​ ⁠ с ​ ² _А + ⁠ 1/2 ​ ⁠ с ​ ² _D , когда доминирование не упускается из виду!

Средний родитель и потомство (MPO)

Поскольку существует множество комбинаций родительских генотипов, необходимо учитывать множество различных способов получения средних родителей и потомков, а также различную частоту получения каждой родительской пары. Генно-модельный подход в данном случае является наиболее целесообразным. Таким образом, нескорректированная сумма перекрестных произведений (USCP) — с использованием всех продуктов { частота родительской пары * эффект среднего родительского гена * среднее значение генотипа потомства } — корректируется путем вычитания {общего среднего генотипического значения} ² в качестве поправочного коэффициента (CF) . После умножения всех различных комбинаций, тщательного сбора терминов, упрощения, факторизации и сокращения, где это применимо, это становится:

cov(MPO) = pq [a + (qp)d ] ² = pq а ² = ⁠ 1/2 ​ ⁠ с ​ ² _A , причем в данном случае не было упущено из виду доминирование, поскольку оно было использовано при определении a .

Приложения (родитель-потомок)

Наиболее очевидным применением является эксперимент, в котором участвуют все родители и их потомки, с взаимным скрещиванием или без него, предпочтительно воспроизведенный без систематической ошибки, позволяющий оценить все соответствующие средние значения, дисперсии и ковариации, а также их стандартные ошибки. Эти приблизительные статистические данные затем можно использовать для оценки генетических отклонений. Двойная разница между оценками двух форм (скорректированной) ковариации родитель-потомок дает оценку s ² _Д ; и удвоенная cov(MPO) оценка s ² _А. ​При соответствующем экспериментальном планировании и анализе Стандартные ошибки также могут быть получены для этой генетической статистики. Это основная суть эксперимента, известного как анализ Диаллеля , версия которого Мэзера, Джинкса и Хеймана обсуждается в другом разделе.

Второе приложение предполагает использование регрессионного анализа , который оценивает на основе статистики ординату (оценка Y), производную (коэффициент регрессии) и константу (пересечение Y) исчисления. Коэффициент регрессии оценивает скорость изменения функции, прогнозирующей Y от X , на основе минимизации остатков между подобранной кривой и наблюдаемыми данными (MINRES). Никакой альтернативный метод оценки такой функции не удовлетворяет этому основному требованию MINRES. В общем, коэффициент регрессии оценивается как отношение ковариации (XY) к дисперсии определителя (X) . На практике размер выборки обычно одинаков для X и Y, поэтому его можно записать как SCP(XY)/SS(X) , где все термины были определены ранее. В данном контексте родители рассматриваются как «определяющая переменная» (X), потомство — как «определяемая переменная» (Y), а коэффициент регрессии — как «функциональная связь» (ßPO ₎ между ними. Принимая cov(MPO) = ⁠ 1/2 ​ ⁠ с ​ ² _A как cov(XY) и s ² _P / 2 (дисперсия среднего значения двух родителей — среднего родителя) как s ² _X , видно, что ß _MPO = [ ⁠ 1/2 ​ ⁠ с ​ ² _А ] / [ ⁠ 1/2 ​ ⁠ с ​ ² _п ] = час ² . Далее, используя cov(PO) = [ ⁠ 1/2 ​ ⁠ с ​ ² _А + ⁠ 1/2 ​ ⁠ с ​ ² _D ] как cov(XY) и s ² _{Проходить} ​ ​ ² _X , видно, что 2 ß _PO = [ 2 ( ⁠ 1/2 ​ ⁠ с ​ ² _А + ⁠ 1/2 ​ ⁠ с ​ ² _Д )]/с ² _П = Ч ² .

Анализ эпистаза ранее предпринимался с использованием дисперсионного подхода типа s. ² _АА и с ² _{нашей эры} , а также с ² _ДД . Это было интегрировано с этими существующими ковариациями, чтобы предоставить оценки эпистазных дисперсий. Однако результаты эпигенетики предполагают, что это может быть неподходящим способом определения эпистаза.

Ковариации братьев и сестер

Ковариантность между полусибсами ( HS ) легко определяется с помощью методов аллельной замены; но, опять же, вклад доминирования исторически не учитывался. Однако, как и в случае с ковариацией среднего родителя/потомка, ковариация между полными сибсами ( FS ) требует подхода «родительской комбинации», что делает необходимым использование метода перекрестного произведения с поправкой на модель гена; и вклад доминирования исторически не упускался из виду. Превосходство производных генной модели здесь так же очевидно, как и генотипических вариаций.

Полуродные братья одного и того же общего родителя (HS)

Сумма перекрестных произведений {частота общего родителя * значение половинного разведения одного полусибса * значение половинного разведения любого другого полусибса в той же группе общих родителей} немедленно дает одно из требуемых ковариации, поскольку используемые эффекты [ породные значения , представляющие ожидания замены аллелей] уже определены как отклонения от генотипического среднего значения [см. раздел «Замена аллелей – Ожидания и отклонения»]. После упрощения. это становится: cov(HS) _A = ⁠ 1 / 2 ⁠ pq а ² = ⁠ 1/4 ​ ⁠ с ​ ² _А. ​ Однако отклонения замещения также существуют, определяя сумму перекрестных произведений { частота общего родителя * отклонение полузамены одного полуродственного брата * отклонение полузамены любого другого полуродителя в том же общем родителе -group } , что в конечном итоге приводит к: cov(HS) _D = p ² д ² д ² = ⁠ 1/4 ​ ⁠ с ​ ² _Д. ​Добавление двух компонентов дает:

cov(HS) = cov(HS) _A + cov(HS) _D = ⁠ 1/4 ​ ⁠ с ​ ² _А + ⁠ 1/4 ​ ⁠ с ​ ² _Д. ​

Полные братья и сестры (FS)

Как пояснялось во введении, используется метод, аналогичный методу, используемому для ковариации средних родителей/потомков. Таким образом, нескорректированная сумма перекрестных произведений (USCP) с использованием всех продуктов — { частота родительской пары * квадрат среднего генотипа потомка } — корректируется путем вычитания {общего среднего генотипического значения} ² в качестве поправочного коэффициента (CF) . В этом случае перемножение всех комбинаций, тщательный сбор членов, упрощение, факторизация и вычитание занимают очень много времени. В конечном итоге это становится:

cov(FS) = pq a ² + р ² д ² д ² = ⁠ 1/2 ​ ⁠ с ​ ² _А + ⁠ 1/4 ​ ⁠ с ​ ² _D , при этом ни одно доминирование не было упущено из виду.

Приложения (братья и сестры)

Наиболее полезным применением генетической статистики здесь является корреляция между полусибсами . Напомним, что коэффициент корреляции ( r ) представляет собой отношение ковариации к дисперсии (см., например, раздел «Связанные атрибуты»). Следовательно, r _HS = cov(HS)/s ² _{все ГС вместе} = [ ⁠ 1/4 ​ ⁠ с ​ ² _А + ⁠ 1/4 ​ ⁠ с ​ ² _Д ]/с ² _П = ⁠ 1 / 4 ⁠ Ч ² . Корреляция между полными сибсами малополезна: r _FS = cov(FS)/s. ² _{все ФС вместе} = [ ⁠ 1/2 ​ ⁠ с ​ ² _А + ⁠ 1/4 ​ ⁠ с ​ ² _Д ]/с ² _П. ​Предположение о том, что оно «приближает» ( ⁠ 1/2 ​ ⁠ ч ​ ² ) плохой совет.

Конечно, корреляции между братьями и сестрами представляют интерес сами по себе, совершенно независимо от какой-либо полезности, которую они могут иметь для оценки наследственности или генотипических различий.

Возможно, стоит отметить, что [ cov(FS) − cov(HS)] = ⁠ 1/4 ​ ⁠ с ​ ² _А. ​Эксперименты, состоящие из семейств FS и HS, могли бы использовать это, используя внутриклассовую корреляцию для приравнивания компонентов дисперсии эксперимента к этим ковариациям (обоснование этого см. в разделе «Коэффициент связи как внутриклассовая корреляция»).

Более ранние комментарии относительно эпистаза снова применимы и здесь [см. раздел «Применение (родители-потомки»).

Выбор

Основные принципы

Генетический прогресс и давление отбора повторяются

Отбор действует на основе атрибута (фенотипа), так что особи, которые равны или превышают порог отбора (z _P ), становятся эффективными родителями для следующего поколения. Доля , которую они представляют в базовой популяции, является давлением отбора . Чем меньше доля, тем сильнее давление. Среднее значение выбранной группы (P _s ) превосходит среднее значение базовой совокупности (P ₀ ) за счет разницы, называемой дифференциалом выбора (S) . Все эти величины фенотипичны. Чтобы «связаться» с лежащими в основе генами, наследственность (h ² ) используется, выполняя роль коэффициента детерминации в биометрическом смысле. Ожидаемое генетическое изменение , все еще выраженное в фенотипических единицах измерения , называется генетическим прогрессом (ΔG) и получается как произведение дифференциала отбора (S) и его коэффициента детерминации (h). ² ) . Ожидаемое среднее значение потомства (P ₁ ) находится путем прибавления генетического прогресса (ΔG) к базовому среднему значению (P ₀ ) . Графики справа показывают, как (начальный) генетический прогресс увеличивается при более сильном давлении отбора (меньшая вероятность ). Они также показывают, как прогресс от последовательных циклов отбора (даже при одном и том же давлении отбора) неуклонно снижается, поскольку фенотипическая дисперсия и наследственность уменьшаются самим отбором. Это обсуждается далее в ближайшее время.

Таким образом $\Delta G=Sh^{2}$. и $P_{1}=P_{0}+\Delta G$.

Узкосмысловая наследственность (h ² ) обычно используется, тем самым связываясь с генной дисперсией (σ ² _А ) . Однако, если это уместно, использование наследственности в широком смысле (H ² ) будет связано с генотипической дисперсией (σ ² _Г ) ; и даже, возможно, аллельная наследственность [ h ² _я = (σ ² _а )/(п ² _P ) ] можно рассматривать как соединение с ( σ ² _а ). [См. раздел «Наследственность».]

Чтобы применить эти концепции до того, как отбор действительно произойдет, и таким образом спрогнозировать результат альтернатив (например, выбора порога отбора ), эти фенотипические статистические данные пересматриваются с учетом свойств нормального распределения, особенно тех, которые касаются усечения превосходный хвост распределения. При таком рассмотрении стандартизованный дифференциал отбора (i)″ и стандартизированный вместо предыдущих «фенотипических» версий используются фенотипическое стандартное отклонение (σ _P(0) ) порог отбора (z)″. Также необходимо . Это описано в следующем разделе.

Следовательно, ΔG = (i σ _P ) h ² , где (i σ _P(0) ) = S ранее.

Изменения, возникающие в результате повторного выбора

В приведенном выше тексте отмечено, что последовательные ΔG снижаются, потому что «входные данные» [ фенотипическая дисперсия ( σ ² _P ) ] уменьшается по сравнению с предыдущим выбором. Наследственность также снижена. Графики слева показывают это снижение в течение десяти циклов повторного отбора, в течение которых утверждается то же самое давление отбора. В этом примере накопленный генетический прогресс ( ΣΔG ) практически достиг своей асимптоты к шестому поколению. Это снижение частично зависит от свойств усечения нормального распределения, а частично от наследственности вместе с определением мейоза ( b ² ) . Последние два пункта количественно определяют степень, в которой усечение «компенсируется» новыми вариациями, возникающими в результате сегрегации и ассортимента во время мейоза. Это скоро будет обсуждаться, но здесь обратите внимание на упрощенный результат для недисперсного случайного оплодотворения (f = 0) .

Таким образом: σ ² _Р(1) = р ² _P(0) [1 − я ( из) ⁠ 1/2 ​ ⁠ ч ​ ² ] , где i ( iz) = K = коэффициент усечения и ⁠ 1/2 ​ ⁠ ч ​ ² = R = коэффициент воспроизводства Это можно записать также как σ ² _Р(1) = р ² _P(0) [1 − KR] , что облегчает более детальный анализ задач выбора.

Здесь i и z уже определены, ⁠ 1 / 2 ⁠ — детерминация мейоза ( б ² ) для f=0 , а оставшийся символ — это наследственность. Они обсуждаются далее в следующих разделах. Также обратите внимание, что в более общем смысле R = b ² час ² . Если определение общего мейоза ( b ² ) результаты предшествующего инбридинга могут быть включены в отбор. Тогда уравнение фенотипической дисперсии принимает вид:

п ² _Р(1) = р ² _P(0) [1 − i ( iz) b ² час ² ] .

Фенотипическая дисперсия, усеченная выбранной группой ( σ ² _P(S) ) — это просто σ ² _P(0) [1 − K] , а его содержащаяся генная дисперсия равна (h ² ₀ п ² _П(С) ). Предполагая, что отбор не изменил изменчивость окружающей среды , генетическую изменчивость потомства можно аппроксимировать σ ² _А(1) = ( п ² _П(1) - п ² _Е ) . Исходя из этого, ч ² ₁ = (п ² _А(1) /п ² _Р(1) ) . Аналогичные оценки можно сделать и для σ ² _Г(1) и Н ² ₁ или для σ ² _а(1) и ч ² _eu(1), если требуется.

Альтернативный вариант ΔG

Следующая перестановка полезна для рассмотрения выбора по нескольким атрибутам (символам). Он начинается с расширения наследственности на компоненты дисперсии. ΔG = я σ _P ( σ ² _А /п ² _П ) ​σ σ _P и ​ ² _P частично отменить, оставив соло σ _P . Далее, σ ² _A внутри наследуемости можно разложить как ( σ _A × σ _A ), что приводит к:

Дифференциал отбора и нормальное распределение

ΔG знак равно я σ _А ( σ _А / σ _п ) знак равно я σ _А час .

Соответствующие перестановки могут быть сделаны с использованием альтернативных наследственных свойств, давая ΔG = i σ _или eu ΔG = i σ _a h _GH .

Модели полигенной адаптации в популяционной генетике

Этот традиционный взгляд на адаптацию в количественной генетике обеспечивает модель того, как выбранный фенотип меняется со временем в зависимости от дифференциала отбора и наследственности. Однако он не дает понимания (и не зависит от) каких-либо генетических деталей - в частности, количества задействованных локусов, частот их аллелей и размеров эффекта, а также изменений частоты, вызванных отбором. Это, напротив, является предметом работ по полигенной адаптации. в области популяционной генетики . Недавние исследования показали, что такие черты, как рост, развились у людей за последние несколько тысяч лет в результате небольших сдвигов частоты аллелей в тысячах вариантов, влияющих на рост.

Фон

Стандартизированный отбор – нормальное распределение

Вся базовая совокупность очерчена нормальной кривой. Направо. По оси Z отложено каждое значение атрибута от наименьшего до наибольшего, а высота от этой оси до самой кривой — это частота значения на оси ниже. Уравнение нахождения этих частот для «нормальной» кривой (кривой «общего опыта») представлено в виде эллипса. Обратите внимание, что он включает в себя среднее значение ( µ ) и дисперсию ( σ ² ). Бесконечно перемещаясь вдоль оси z, частоты соседних значений могут «складываться» рядом с предыдущими, тем самым накапливая область, которая представляет вероятность получения всех значений в стеке. [Это интеграция из исчисления.] Отбор фокусируется на такой вероятностной области, которая представляет собой заштрихованную область от порога выбора (z) до конца верхнего хвоста кривой. Это давление отбора . Выбранная группа (эффективные родители следующего поколения) включает все значения фенотипа от z до «конца» хвоста. Среднее значение выбранной группы — μ _s , а разница между ним и базовым средним значением ( μ ) представляет собой дифференциал выбора (S) . Путем частичного интегрирования по интересующим участкам кривой и некоторой перестановки алгебры можно показать, что «дифференциал выбора» равен S = [ y (σ / Prob.)] , где y — частота значения в точке порог выбора» z ( ордината z « ). Перестановка этого соотношения дает S/σ = y/Prob. , левая часть которого, по сути, представляет собой дифференциал отбора, разделенный на стандартное отклонение , — это стандартизированный дифференциал отбора (i) . Правая часть соотношения представляет собой «оценщик» для i — ординаты порога выбора, деленной на давление выбора . Таблицы нормального распределения можно использовать, но i . также доступны таблицы самого Последняя ссылка также дает значения i , скорректированные для небольших популяций (400 и меньше), где «квазибесконечность» не может быть принята (но предполагалась в схеме «Нормального распределения» выше). Стандартизованный дифференциал отбора ( i ) известен также как интенсивность отбора .

Наконец, может оказаться полезной перекрестная связь с другой терминологией из предыдущего подраздела: μ (здесь) = «P ₀ » (там), μ _S = « _PS » и σ. ² = "σ ² _П ».

Определение мейоза – анализ репродуктивного пути

Репродуктивные коэффициенты детерминации и инбридинга

Анализ пути полового размножения.

Определение мейоза (b ² ) — коэффициент детерминации мейоза, то есть деления клеток, в результате которого родители образуют гаметы. Следуя принципам стандартизированной частичной регрессии , графической версией которой является анализ путей , Сьюэлл Райт проанализировал пути потока генов во время полового размножения и установил «силы вклада» ( коэффициенты детерминации ) различных компонентов в общий результат. результат. Анализ пути включает в себя частичные корреляции , а также коэффициенты частичной регрессии (последние являются коэффициентами пути ). Линии с одинарным наконечником стрелки представляют собой определяющие направления пути , а линии с двойными наконечниками стрелок являются корреляционными связями . Отслеживание различных маршрутов в соответствии с правилами анализа путей имитирует алгебру стандартизированной частичной регрессии.

Диаграмма пути слева представляет этот анализ полового размножения. Из его интересных элементов важным в контексте отбора является мейоз . Именно здесь происходят сегрегация и ассортимент — процессы, которые частично смягчают сокращение фенотипической вариативности, возникающей в результате отбора. Коэффициенты пути b представляют собой пути мейоза. Те, что отмечены буквой a, представляют собой пути оплодотворения. Корреляция между гаметами одного родителя ( g ) — мейотическая корреляция . Между родителями одного поколения есть r _A . Коэффициент между гаметами от разных родителей ( f ) впоследствии стал называться коэффициентом инбридинга . Штрихи (') обозначают поколение (t-1) , а незаштрихованные указывают поколение t . Здесь приведены некоторые важные результаты настоящего анализа. Сьюэлл Райт интерпретировал многие из них с точки зрения коэффициентов инбридинга.

Определение мейоза ( b ² ) является ⁠ 1/2 и равно ⁠ +g) ( 1 ⁠ 1/2 g (t - ⁠ (1 + f _(t-1) ) , подразумевая, что = f ₁₎ . При недисперсном случайном внесении f _(t-1) ) = 0, что дает b ² = ⁠ 1 / 2 ⁠ , как указано в разделе выбора выше. Однако, зная об этом, при необходимости можно использовать и другие схемы внесения удобрений. Еще одно определение также включает в себя инбридинг — определение оплодотворения ( а ² ) равно 1 / [ 2 ( 1 + ж _т ) ] . Также еще одной корреляцией является показатель инбридинга — r _A = 2 f _t / ( 1 + f _(t-1) ) , также известный как коэффициент родства . [Не путайте это с коэффициентом родства — альтернативным названием коэффициента родства . См. введение к разделу «Взаимосвязи».] Это r _A снова встречается в подразделе, посвященном дисперсии и отбору.

Эти связи с инбридингом открывают интересные аспекты полового размножения, которые не очевидны сразу. На графиках справа показаны мейоза и сингамии (оплодотворения) коэффициенты детерминации в зависимости от коэффициента инбридинга. Там выявлено, что по мере усиления инбридинга большее значение приобретает мейоз (увеличивается коэффициент), а сингамия становится менее значимой. Общая роль воспроизводства (произведение двух предыдущих коэффициентов — r ² ] остается прежним. Это увеличение b ² особенно актуально для отбора, поскольку это означает, что сокращение фенотипической дисперсии при отборе компенсируется в меньшей степени во время последовательности отборов, когда оно сопровождается инбридингом (что часто имеет место).

Генетический дрейф и отбор

В предыдущих разделах дисперсия рассматривалась как «помощник» отбора , и стало очевидно, что они хорошо работают вместе. В количественной генетике отбор обычно исследуется таким «биометрическим» способом, но изменения в средних значениях (отслеживаемые по ΔG) отражают изменения частот аллелей и генотипов под этой поверхностью. Обращение к разделу «Генетический дрейф» заставляет вспомнить, что он также влияет на изменения частот аллелей и генотипов и связанные с ними средства; и что это сопутствующий аспект рассматриваемой здесь дисперсии («другая сторона одной медали»). Однако эти две силы изменения частоты редко действуют согласованно и часто могут действовать вопреки друг другу. Один (отбор) является «направленным» и обусловлен давлением отбора, действующим на фенотип: другой (генетический дрейф) обусловлен «случайностью» оплодотворения (биномиальными вероятностями образцов гамет). Если они имеют тенденцию к одной и той же частоте аллелей, их «совпадение» — это вероятность получения образца этих частот в результате генетического дрейфа; однако вероятность того, что они находятся «в конфликте», является сумма вероятностей всех альтернативных выборок частоты . В крайних случаях одна-единственная выборка сингамии может свести на нет то, чего достиг отбор, и вероятности того, что это произойдет, известны. Важно помнить об этом. Однако генетический дрейф, приводящий к тому, что частоты выборки аналогичны частотам выборки, не приводит к столь радикальному результату, а вместо этого замедляет прогресс в достижении целей отбора.

Коррелирующие атрибуты

При совместном наблюдении двух (или более) атрибутов ( например, роста и массы) можно заметить, что они изменяются вместе по мере изменения генов или окружающей среды. Эта ковариация измеряется ковариацией , которая может быть представлена ​​как « cov » или θ . Будет положительно, если они изменяются вместе в одном и том же направлении; или отрицательным, если они изменяются вместе, но в противоположном направлении. Если два атрибута изменяются независимо друг от друга, ковариация будет равна нулю. Степень связи между атрибутами количественно оценивается коэффициентом корреляции (символ r или ρ ). В общем, коэффициент корреляции представляет собой отношение ковариации к среднему геометрическому. из двух вариантов атрибутов. Наблюдения обычно происходят на фенотипе, но в исследованиях они также могут происходить на «эффективном гаплотипе» (эффективном генном продукте) (см. рисунок справа). Таким образом, ковариация и корреляция могут быть «фенотипическими», «молекулярными» или любыми другими обозначениями, которые допускает модель анализа. Фенотипическая ковариация является «самым внешним» уровнем и соответствует «обычной» ковариации в биометрии/статистике. Однако ее можно разделить с помощью любой подходящей исследовательской модели так же, как и фенотипическую дисперсию. Каждому разделу ковариации соответствует соответствующий раздел корреляции. Некоторые из этих разделов приведены ниже. Первый нижний индекс (G, A и т. д.) указывает на раздел. Индексы второго уровня (X, Y) являются «хранителями места» для любых двух атрибутов.

Источники фенотипической корреляции.

Первый пример — неразделенный фенотип.

${r_{P_{XY}}}={{cov_{P_{XY}}} \over {\sqrt {\sigma _{P_{X}}^{2}\sigma _{P_{Y}}^{2}}}}$

Далее следуют генетические разделы (а) «генотипические» (общий генотип), (б) «генные» (ожидания замещения) и (в) «аллельные» (гомозиготы).

(а) ${r_{G_{XY}}}={{cov_{G_{XY}}} \over {\sqrt {\sigma _{G_{X}}^{2}\sigma _{G_{Y}}^{2}}}}$

(б) ${r_{A_{XY}}}={{cov_{A_{XY}}} \over {\sqrt {\sigma _{A_{X}}^{2}\sigma _{A_{Y}}^{2}}}}$

(с) ${r_{a_{XY}}}={{cov_{a_{XY}}} \over {\sqrt {\sigma _{a_{X}}^{2}\sigma _{a_{Y}}^{2}}}}$

При правильно спланированном эксперименте негенетическое можно также получить (средовое) разделение.

${r_{E_{XY}}}={{cov_{E_{XY}}} \over {\sqrt {\sigma _{E_{X}}^{2}\sigma _{E_{Y}}^{2}}}}$

Основные причины корреляции

Существует несколько различных способов возникновения фенотипической корреляции. Дизайн исследования, размер выборки, статистика выборки и другие факторы могут влиять на возможность различать их с большей или меньшей статистической достоверностью. Каждый из них имеет различное научное значение и относится к различным областям работы.

Прямая причинно-следственная связь

Один фенотип может напрямую влиять на другой фенотип, влияя на развитие, метаболизм или поведение.

Генетические пути

Общий ген или фактор транскрипции в биологических путях двух фенотипов может привести к корреляции.

Метаболические пути

Метаболические пути от гена к фенотипу сложны и разнообразны, но причины корреляции между признаками лежат внутри них.

Факторы развития и окружающей среды

На несколько фенотипов могут влиять одни и те же факторы. Например, существует множество фенотипических признаков, коррелирующих с возрастом, поэтому рост, вес, потребление калорий, эндокринная функция и многое другое имеют корреляцию. Исследование, направленное на поиск других общих факторов, должно сначала исключить их.

Коррелирующие генотипы и давление отбора

Различия между подгруппами в популяции, между популяциями или селективные предубеждения могут означать, что некоторые комбинации генов представлены в большем количестве по сравнению с тем, что можно было бы ожидать. Хотя гены могут не оказывать существенного влияния друг на друга, между ними все же может существовать корреляция, особенно когда определенным генотипам не разрешено смешиваться. Популяции, находящиеся в процессе генетической дивергенции или уже подвергшиеся ей, могут иметь разные характерные фенотипы. а это значит, что при совместном рассмотрении появляется корреляция. Фенотипические качества человека, преимущественно зависящие от происхождения, также вызывают корреляции этого типа. Это также можно наблюдать у пород собак, где несколько физических особенностей составляют отличительные черты данной породы и, следовательно, коррелируют. Ассортативное спаривание , которое представляет собой сексуальное избирательное давление с целью спаривания со схожим фенотипом, может привести к тому, что генотипы останутся коррелированными в большей степени, чем можно было бы ожидать.

См. также

• Искусственный отбор
• Диаллельный крест
• Дуглас Скотт Фалконер
• Формула выборки Юэнса
• Экспериментальная эволюция
• Вопрос _СТ
• Генетическая архитектура
• Генетическая дистанция
• Наследственность
• Рональд Фишер

Дальнейшее чтение

• Фальконер Д.С. и Маккей TFC ​​(1996). Введение в количественную генетику, 4-е издание. Лонгман, Эссекс, Англия.
• Кабальеро, А. (2020) Количественная генетика. Издательство Кембриджского университета.
• Линч М. и Уолш Б. (1998). Генетика и анализ количественных признаков. Зинауер, Сандерленд, Массачусетс.
• Рофф Д.А. (1997). Эволюционная количественная генетика. Чепмен и Холл, Нью-Йорк.
• Сейкора, Тони. Зоотехника 3221 Животноводство. Тех. Миннеаполис: Университет Миннесоты, 2011. Печать.

Внешние ссылки

• Уравнение заводчика
• Ресурсы по количественной генетике Майкла Линча и Брюса Уолша , включая два тома их учебника « Генетика и анализ количественных признаков» и «Эволюция и отбор количественных признаков» .
• Ресурсы Ника Бартона и др. . из учебника Эволюция .
• G-Матрица Онлайн