Функция вопросительного знака Минковского

Функция вопросительного знака Минковского.

Слева: ?( х ) . Справа: ?( х ) - х .

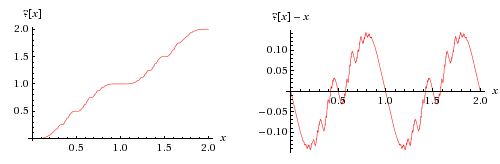
В математике , функция вопросительного знака Минковского обозначаемая ?( x ) , представляет собой функцию с необычными фрактальными свойствами, определенную Германом Минковским в 1904 году. Он отображает квадратичные иррациональные числа в рациональные числа на единичном интервале с помощью выражения, связывающего в непрерывную дробь разложение квадратичных чисел с двоичным разложением рациональных чисел, данного Арно Данжуа в 1938 году. Он также отображает рациональные числа в двоичные рациональные числа , как можно видеть из рекурсивного определения, тесно связанного с деревом Штерна-Броко .

Определение и интуиция

Один из способов определения функции вопросительного знака включает в себя соответствие между двумя различными способами представления дробных чисел с использованием конечных или бесконечных двоичных последовательностей . Наиболее привычно, что строка из 0 и 1 с одной точкой «.», например «11.001001000011111...», может интерпретироваться как двоичное представление числа. В данном случае это число

$$2+1+{\frac {1}{8}}+{\frac {1}{64}}+\cdots =\pi .$$

Однако существует другой способ интерпретации той же последовательности, используя цепные дроби . Интерпретируя дробную часть «0,001001000011111...» как двоичное число таким же образом, замените каждый последовательный блок из 0 или 1 на длину его серии (или, для первого блока нулей, длину его серии плюс единица), в этом случай, генерирующий последовательность $[3;3,1,2,1,4,5,\dots ]$. Затем используйте эту последовательность в качестве коэффициентов цепной дроби:

$$3+{\frac {1}{\displaystyle 3+{\frac {1}{\displaystyle 1+{\frac {1}{\displaystyle 2+{\frac {1}{\displaystyle 1+{\frac {1}{\displaystyle 4+{\frac {1}{\displaystyle 5+\dots }}}}}}}}}}}}\approx 3.2676$$

Функция вопросительного знака обращает этот процесс: она переводит непрерывную дробь данного действительного числа в двоичную последовательность, закодированную по длине, а затем переинтерпретирует эту последовательность как двоичное число. Например, для примера выше, $\operatorname {?} (3.2676)\approx \pi$. Чтобы определить это формально, если иррациональное число $x$ имеет (неокончательное) представление цепной дроби

$$x=a_{0}+{\frac {1}{\displaystyle a_{1}+{\frac {1}{\displaystyle a_{2}+\cdots }}}}=[a_{0};a_{1},a_{2},\dots ]$$

тогда значение функции вопросительного знака на $x$ определяется как значение бесконечного ряда

$$\operatorname {?} (x)=a_{0}+2\sum _{n=1}^{\infty }{\frac {\left(-1\right)^{n+1}}{2^{a_{1}+\cdots +a_{n}}}}.$$

Аналогично, если рациональное число $x$ имеет конечное представление непрерывной дроби $[a_{0};a_{1},a_{2},\dots ,a_{m}]$ затем значение функции вопросительного знака на $x$ представляет собой конечную сумму,

$$\operatorname {?} (x)=a_{0}+2\sum _{n=1}^{m}{\frac {\left(-1\right)^{n+1}}{2^{a_{1}+\cdots +a_{n}}}}.$$

Аналогично тому, как функция вопросительного знака интерпретирует непрерывные дроби как двоичные числа, функцию Кантора можно понимать как интерпретацию троичных чисел как двоичные числа.

Самосимметрия

Вопросительный знак явно визуально самоподобен. Моноид действующими на самоподобий может быть порожден двумя операторами S и R, единичном квадрате, и определяться следующим образом:

$${\begin{aligned}S(x,y)&=\left({\frac {x}{x+1}},{\frac {y}{2}}\right),\\[5px]R(x,y)&=(1-x,1-y).\end{aligned}}$$

Визуально S сжимает единичный квадрат до его нижней левой четверти, а R выполняет точечное отражение через его центр.

Точка графике ? на имеет координаты ( x , ?( x )) для некоторого x в единичном интервале. Такая точка преобразуется S и R в другую точку графика, потому что ? удовлетворяет следующим тождествам для всех x ∈ [0, 1] :

$${\begin{aligned}\operatorname {?} \left({\frac {x}{x+1}}\right)&={\frac {\operatorname {?} (x)}{2}},\\[5px]\operatorname {?} (1-x)&=1-\operatorname {?} (x).\end{aligned}}$$

Эти два оператора можно многократно комбинировать, образуя моноид. Тогда общим элементом моноида будет

$$S^{a_{1}}RS^{a_{2}}RS^{a_{3}}\cdots$$

для натуральных чисел a ₁ , a ₂ , a ₃ , … . Каждый такой элемент описывает самоподобие функции вопросительного знака. Этот моноид иногда называют моноидом удвоения периода , и все фрактальные кривые с удвоением периода имеют описываемую им самосимметрию ( кривая де Рама , частным случаем которой является вопросительный знак, является категорией таких кривых). Элементам моноида соответствуют рациональные числа посредством отождествления a ₁ , a ₂ , a ₃ , … с цепной дробью [0; а ₁ , а ₂ , а ₃ ,…] . Поскольку оба

$$S:x\mapsto {\frac {x}{x+1}}$$

и

$$T:x\mapsto 1-x$$

являются дробно-линейными преобразованиями с целыми коэффициентами, моноид можно рассматривать как подмножество модулярной группы PSL(2, Z ) .

Квадратичные иррациональные числа

Функция вопросительного знака обеспечивает взаимно однозначное отображение недвоичных рациональных чисел в квадратичные иррациональные числа , что позволяет явно доказать счетность последних. Фактически, их можно понимать как соответствующие периодическим орбитам диадического преобразования . Это можно наглядно продемонстрировать всего за несколько шагов.

Диадическая симметрия

Определите два хода: ход влево и ход вправо, действительные на единичном интервале. $0\leq x\leq 1$ как

$$L_{D}(x)={\frac {x}{2}}$$

и $L_{C}(x)={\frac {x}{1+x}}$ и

$$R_{D}(x)={\frac {1+x}{2}}$$

и $R_{C}(x)={\frac {1}{2-x}}$ Тогда функция вопросительного знака подчиняется симметрии движения влево.

$$L_{D}\circ {\text{?}}={\text{?}}\circ L_{C}$$

и правая симметрия

$$R_{D}\circ {\text{?}}={\text{?}}\circ R_{C}$$

где $\circ$ обозначает композицию функций . Они могут быть произвольно объединены. Рассмотрим, например, последовательность ходов влево-вправо. $LRLLR.$ Добавление индексов C и D и, для ясности, удаление оператора композиции. $\circ$ почти во всех местах, за исключением нескольких, есть:

$$L_{D}R_{D}L_{D}L_{D}R_{D}\circ {\text{?}}={\text{?}}\circ L_{C}R_{C}L_{C}L_{C}R_{C}$$

Произвольные строки конечной длины в буквах L и R соответствуют двоично-рациональным числам , поскольку каждое двоично-рациональное число может быть записано как $y=n/2^{m}$ для целых чисел n и m и как конечная длина битов $y=0.b_{1}b_{2}b_{3}\cdots b_{m}$ с $b_{k}\in \{0,1\}.$ Таким образом, каждое двоичное рациональное находится во взаимно однозначном соответствии с некоторой самосимметрией функции вопросительного знака.

Некоторые изменения в обозначениях могут немного облегчить выражение вышеизложенного. Позволять $g_{0}$ и $g_{1}$ обозначают L и R. Композиция функций расширяет это до моноида , поскольку можно написать $g_{010}=g_{0}g_{1}g_{0}$ и вообще, $g_{A}g_{B}=g_{AB}$ для некоторых двоичных строк цифр A , B , где AB — это обычная конкатенация таких строк. Тогда диадический моноид M является моноидом всех таких движений конечной длины влево-вправо. Письмо $\gamma \in M$ как общий элемент моноида, имеется соответствующая самосимметрия функции вопросительного знака:

$$\gamma _{D}\circ {\text{?}}={\text{?}}\circ \gamma _{C}$$

Изоморфизм

Явное отображение между рациональными числами и двоичными рациональными числами может быть получено с помощью оператора отражения

$$r(x)=1-x$$

и отмечая, что оба

$$r\circ R_{D}\circ r=L_{D}$$

и $r\circ R_{C}\circ r=L_{C}$ С $r^{2}=1$ является тождеством, произвольную строку ходов влево-вправо можно переписать как строку только ходов влево, за которой следует отражение, за которым следуют еще ходы влево, отражение и т. д., то есть как $L^{a_{1}}rL^{a_{2}}rL^{a_{3}}\cdots$ который явно изоморфен $S^{a_{1}}TS^{a_{2}}TS^{a_{3}}\cdots$ сверху. Вычисление некоторой явной последовательности $L_{D},R_{D}$ в аргументе функции $x=1$ дает двойственное рациональное мышление; явно, оно равно $y=0.b_{1}b_{2}b_{3}\cdots b_{m}$ где каждый $b_{k}\in \{0,1\}$ — двоичный бит: ноль соответствует перемещению влево, а единица соответствует перемещению вправо. Эквивалентная последовательность $L_{C},R_{C}$ ходы, оцененные в $x=1$ дает рациональное число $p/q.$ Это явно та, которую дает цепная дробь $p/q=[a_{1},a_{2},a_{3},\ldots ,a_{j}]$ имея в виду, что это рационально, потому что последовательность $(a_{1},a_{2},a_{3},\ldots ,a_{j})$ имел конечную длину. Это устанавливает взаимно однозначное соответствие между диадическими рациональными и рациональными.

диадического

Рассмотрим теперь периодические орбиты двоичного преобразования . Они соответствуют битовым последовательностям, состоящим из конечной исходной «хаотичной» последовательности битов. $b_{0},b_{1},b_{2},\ldots ,b_{k-1}$, за которым следует повторяющаяся строка $b_{k},b_{k+1},b_{k+2},\ldots ,b_{k+m-1}$ длины $m$. Такие повторяющиеся строки соответствуют рациональному числу. Это легко сделать явным. Писать

$$y=\sum _{j=0}^{m-1}b_{k+j}2^{-j-1}$$

тогда явно есть

$$\sum _{j=0}^{\infty }b_{k+j}2^{-j-1}=y\sum _{j=0}^{\infty }2^{-jm}={\frac {y}{1-2^{m}}}$$

Учитывая исходную неповторяющуюся последовательность, мы явно имеем рациональное число. Фактически, каждое рациональное число можно выразить таким образом: начальная «случайная» последовательность, за которой следует циклическое повторение. То есть периодические орбиты карты находятся во взаимно однозначном соответствии с рациональными числами.

орбиты как

Такие периодические орбиты имеют эквивалентную периодическую цепную дробь в соответствии с установленным выше изоморфизмом. Существует начальная «хаотическая» орбита некоторой конечной длины, за которой следует повторяющаяся последовательность. Повторяющаяся последовательность порождает периодическую цепную дробь, удовлетворяющую $x=[a_{n},a_{n+1},a_{n+2},\ldots ,a_{n+r},x].$ Эта непрерывная дробь имеет вид

$$x={\frac {\alpha x+\beta }{\gamma x+\delta }}$$

с $\alpha ,\beta ,\gamma ,\delta$ являются целыми числами и удовлетворяют $\alpha \delta -\beta \gamma =\pm 1.$ Явные значения можно получить, написав

$$S\mapsto {\begin{pmatrix}1&0\\1&1\end{pmatrix}}$$

на смену, так что

$$S^{n}\mapsto {\begin{pmatrix}1&0\\n&1\end{pmatrix}}$$

в то время как отражение дается

$$T\mapsto {\begin{pmatrix}-1&1\\0&1\end{pmatrix}}$$

так что $T^{2}=I$. Обе эти матрицы унимодулярны , произвольные произведения остаются унимодулярными и приводят к матрице вида

$$S^{a_{n}}TS^{a_{n+1}}T\cdots TS^{a_{n+r}}={\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}$$

давая точное значение цепной дроби. Поскольку все элементы матрицы являются целыми числами, эта матрица принадлежит проективной модульной группе. $PSL(2,\mathbb {Z} ).$

Решая явно, получаем следующее: $\gamma x^{2}+(\delta -\alpha )x-\beta =0.$ Нетрудно проверить, что решения этой задачи удовлетворяют определению квадратичных иррациональных чисел. Фактически, любое квадратичное иррациональное число можно выразить таким образом. Таким образом, квадратичные иррациональные числа находятся во взаимно однозначном соответствии с периодическими орбитами диадического преобразования, которые находятся во взаимно однозначном соответствии с (недиадическими) рациональными числами, которые находятся во взаимно однозначном соответствии с диадическое рациональное мышление. Функция вопросительного знака обеспечивает соответствие в каждом случае.

Свойства ?( x )

Функция вопросительного знака является строго возрастающей и непрерывной. но не абсолютно непрерывная функция. Производная рациональных определена почти всюду , и может принимать только два значения: 0 (ее значение почти везде, в том числе и у всех чисел ) и $+\infty$. Существует несколько конструкций меры , которая при интегрировании дает функцию вопросительного знака. Одна из таких конструкций получается путем измерения плотности чисел Фарея на прямой числовой линии. Мера вопросительного знака является типичным примером того, что иногда называют мультифрактальными мерами .

Функция вопросительного знака отображает рациональные числа в двоично-рациональные числа , то есть те, представление которых по основанию два заканчивается, что можно доказать индукцией из рекурсивной конструкции, описанной выше. Он отображает квадратичные иррациональные числа в недиадические рациональные числа. В обоих случаях он обеспечивает изоморфизм порядка между этими множествами: формулируя конкретную теорему Кантора об изоморфизме, согласно которой каждые два неограниченных счетных плотных линейных порядка порядково-изоморфны. Это нечетная функция и удовлетворяет функциональному уравнению ?( x + 1) = ?( x ) + 1 ; следовательно, x ↦ ?( x ) − x — нечетная периодическая функция с периодом один. Если ?( x ) иррационально, то x либо алгебраический степени больше двух, либо трансцендентный .

Функция вопросительного знака имеет фиксированные точки в 0, 1/2 как минимум и 1 и еще две, симметричные относительно средней точки. Один примерно равен 0,42037. Мощевитин предположил, что это единственные пять неподвижных точек.

В 1943 году Рафаэль Салем поднял вопрос о том, исчезают ли на бесконечности коэффициенты Фурье – Стилтьеса функции вопросительного знака. Другими словами, он хотел знать, действительно ли

$$\lim _{n\to \infty }\int _{0}^{1}e^{2\pi inx}\,\operatorname {d?} (x)=0.$$

На этот вопрос Джордан и Салстен ответили утвердительно, как на частный случай результата по мерам Гиббса .

График функции вопросительного знака Минковского представляет собой частный случай фрактальных кривых, известных как кривые де Рама .

Алгоритм

Рекурсивное определение естественным образом подходит для алгоритма вычисления функции с любой желаемой степенью точности для любого действительного числа, как C. демонстрирует следующая функция Алгоритм спускается по дереву Штерна-Броко в поисках входных данных x суммирует члены двоичного разложения y = ?( x ) и по пути . Пока инвариант цикла qr − ps = 1 сохраняется, нет необходимости уменьшать дробь м / н = p + r / q + s , так как это уже в низших терминах. Другой инвариант p / q ≤ x < р / с . for цикл в этой программе можно анализировать примерно так же, как while цикл, в котором операторы условного разрыва в первых трех строках определяют условие. Единственные утверждения в цикле, которые могут повлиять на инварианты, находятся в последних двух строках, и можно показать, что они сохраняют истинность обоих инвариантов до тех пор, пока первые три строки выполняются успешно без выхода из цикла. Третий инвариант тела цикла (с точностью до плавающей запятой) — это y ≤ ?( x ) < y + d , но поскольку d уменьшается вдвое в начале цикла перед проверкой каких-либо условий, наш вывод состоит только в том, что y ≤ ?( x ) < y + 2 d в конце цикла.

Для доказательства завершения достаточно заметить, что сумма q + s увеличивается как минимум на 1 с каждой итерацией цикла и что цикл завершится, когда эта сумма станет слишком большой, чтобы ее можно было представить в примитивном типе данных C. long. Однако на практике условный разрыв, когда y + d == y это то, что обеспечивает завершение цикла в разумные сроки.

/* Minkowski's question-mark function */
double minkowski(double x) {
    long p = x;
    long q = 1, r = p + 1, s = 1, m, n;
    double d = 1, y = p;
    if (x < p || (p < 0) ^ (r <= 0))
        return x; /* out of range ?(x) =~ x */
    for (;;) { /* invariants: q * r - p * s == 1 && p / q <= x && x < r / s */
        d /= 2;
        if (y + d == y)
            break; /* reached max possible precision */
        m = p + r;
        if ((m < 0) ^ (p < 0))
            break; /* sum overflowed */
        n = q + s;
        if (n < 0)
            break; /* sum overflowed */

        if (x < (double)m / n) {
            r = m;
            s = n;
        } else {
            y += d;
            p = m;
            q = n;
        }
    }
    return y + d; /* final round-off */
}

Распределение

Ограничив функцию вопросительного знака Минковского до ?:[0,1] → [0,1], ее можно использовать как кумулятивную функцию распределения сингулярного распределения на единичном интервале. Это распределение симметрично относительно своей средней точки, с необработанными моментами примерно m ₁ = 0,5, m ₂ = 0,290926, m ₃ = 0,186389 и m ₄ = 0,126992, таким образом, среднее значение и медиана равны 0,5, стандартное отклонение около 0,2023, асимметрия 0 и избыточный эксцесс около -1,147.

См. также

• Производные Помпея

Ссылки

Исторические источники

• Минковский, Герман (1904), «О геометрии чисел» , Переговоры III. Международный конгресс математиков в Гейдельберге , Берлин, стр. 164–173, JFM   36.0281.01 , заархивировано из оригинала 4 января 2015 г. {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Данжуа, Арно (1938), «О реальной функции Минковского», J. Math. Чистое приложение. , Серия IX (на французском языке), 17 : 105–151, Zbl   0018.34602

Библиография

• Алкаускас, Гедриус ​​(2010), «Моменты функции вопросительного знака Минковского: функция диадического периода», Glasgow Mathematical Journal , 52 (1): 41–64, arXiv : 0801.0051 , doi : 10.1017/S0017089509990152 , MR   2587817 , Идентификатор идентификатора   115167042
• Бхаттачарджи, Минакси; Макферсон, Дугалд; Мёллер, Рёнвальдур Г.; Нойманн, Питер М. (1997), «Рациональные числа», Заметки о бесконечных группах перестановок , Тексты и материалы для чтения по математике, том. 12, Берлин: Springer-Verlag, стр. 77–86, номер документа : 10.1007/978-93-80250-91-5_9 , ISBN.  81-85931-13-5 , МР   1632579
• Душистова Анна Александровна; Мощевитин, Николай Г. (март 2012 г.), «О производной функции вопросительного знака Минковского. $?(x)$", Журнал математических наук , 182 (4): 463–471, arXiv : 0706.2219 , doi : 10.1007/s10958-012-0750-2 , MR   2825515 , S2CID   115156022
• Финч, Стивен Р. (2003), Математические константы , Энциклопедия математики и ее приложений, том. 94, Кембридж : Издательство Кембриджского университета , ISBN  978-0-521-81805-6 , Збл   1054,00001
• Гиргенсон, Роланд (1996), «Построение сингулярных функций с помощью дробей Фарея», Журнал математического анализа и приложений , 203 (1): 127–141, doi : 10.1006/jmaa.1996.0370 , MR   1412484
• Джордан, Томас; Сальстен, Туомас (2016), «Преобразования Фурье мер Гиббса для карты Гаусса», Mathematische Annalen , 364 (3–4): 983–1023, arXiv : 1312.3619 , Bibcode : 2013arXiv1312.3619J , doi : 10.1007/s00208- 015 -1241-9 , S2CID   56046793
• Хинчин, А.Я. (1964) [Первоначально опубликовано на русском языке, 1935], «10: Квадратичные иррациональные числа и периодические цепные дроби», Continuous Fractions , University of Chicago Press , стр. 47–50, ISBN  0-486-69630-8 ; перепечатано Dover Publications, 1997 г.
• Мощевитин, Николай (25 ноября 2020 г.), «Сессия открытых задач», Диофантовы задачи, детерминизм и случайность , CIRM – через YouTube
• Пифей Фогг, Н. (2002), Берте, Валери ; Ференци, Себастьен; Модуит, Кристиан; Сигел, А. (ред.), Замены в динамике, арифметике и комбинаторике , Конспекты лекций по математике, том. 1794, Берлин: Springer-Verlag , ISBN.  978-3-540-44141-0 , Збл   1014.11015
• Салем, Рафаэль (1943), «О некоторых сингулярных монотонных функциях, которые строго возрастают» (PDF) , Transactions of the American Mathematical Society , 53 (3): 427–439, doi : 10.2307/1990210 , JSTOR   1990210

Дальнейшее чтение

• Алкаускас, Гедриус ​​(2008), Интегральные преобразования функции вопросительного знака Минковского , докторская диссертация, Ноттингемский университет
• Бибилони, Л.; Паради, Дж.; Виадер, П. (1998), «Новый взгляд на функцию ?(x) Минковского» , Journal of Number Theory , 73 (2): 212–227, doi : 10.1006/jnth.1998.2294 , hdl : 10230/843 , Zbl   0928.11006 , заархивировано из оригинала 22 июня 2015 г.
• Библони, Л.; Рай, Дж.; Виадер, П. (2001), «Производная сингулярной функции Минковского», Journal of Mathematical Analysis and Applications , 253 (1): 107–125, doi : 10.1006/jmaa.2000.7064 , Zbl   0995.26005
• Конли, Р.М. (2003), Обзор функции Минковского ?(x) , магистерская диссертация, Университет Западной Вирджинии.
• Конвей, Дж. Х. (2000), «Искаженные дроби», О числах и играх (2-е изд.), Уэлсли, Массачусетс: AK Peters, стр. 82–86.
• Вепстас, Л. (2004), Вопросительный знак Минковского и модульная группа SL (2, Z) (PDF)
• Вепстас, Л. (2008), «О мере Минковского», arXiv : 0810.1265 [ math.DS ]

Внешние ссылки

• Обширный список библиографии
• Вайсштейн, Эрик В. , «Функция вопросительного знака Минковского» , MathWorld
• Простая реализация IEEE 754 на C++