Диадический рациональный

В математике двоично-рациональное или двоично-рациональное число — это число, которое можно выразить в виде дроби которого , знаменатель равен степени двойки . Например, 1/2, 3/2 и 3/8 являются двоичными рациональными числами, а 1/3 – нет. Эти числа важны в информатике , поскольку только они имеют конечное двоичное представление . Диадическое рациональное мышление также находит применение в измерениях и весах, музыкальных размерах и раннем математическом образовании. Они могут точно аппроксимировать любое действительное число .

Сумма, разность или произведение любых двух двоично-рациональных чисел — это еще одно двоично-рациональное число, заданное простой формулой. Однако деление одного двоично-рационального числа на другое не всегда дает двоично-рациональный результат. Математически это означает, что двоичные рациональные числа образуют кольцо , лежащее между кольцом целых чисел и полем рациональных чисел . Это кольцо можно обозначить $\mathbb {Z} [{\tfrac {1}{2}}]$ .

В высшей математике двоичные рациональные числа занимают центральное место в конструкциях двоичного соленоида , функции вопросительного знака Минковского , вейвлетов Добеши , группы Томпсона , 2-группы Прюфера , сюрреалистических чисел и плавких чисел . Эти числа по порядку изоморфны рациональным числам; они образуют подсистему 2-адических чисел , а также действительных чисел и могут представлять дробные части 2-адических чисел. Функции от натуральных чисел до двоично-рациональных чисел использовались для формализации математического анализа в обратной математике .

Приложения

В измерении

Кухонные гири, измеряющие двоичные доли фунта от 2 фунтов до 1/64 фунта (1/4 унции)

Многие традиционные системы мер и весов основаны на идее повторяющегося деления пополам, что приводит к получению двоичных рациональных чисел при измерении дробных количеств единиц. Дюймы обычно делятся на двоичные рациональные числа , а не на десятичные. ^[1] Обычное деление галлона на полгаллона, кварту , пинту и чашку также является диадическим. ^[2] Древние египтяне использовали для измерения диадические рациональные числа со знаменателями до 64. ^[3] Точно так же системы весов цивилизации долины Инда по большей части основаны на многократном делении пополам; антрополог Хизер М.-Л. Миллер пишет, что «деление пополам — это относительно простая операция с весами, и, вероятно, поэтому во многих системах весов того периода времени использовались двоичные системы». ^[4]

В вычислительной технике

Диадические рациональные числа занимают центральное место в информатике как тип дробных чисел, которыми многие компьютеры могут напрямую манипулировать. ^[5] В частности, как тип данных, используемый компьютерами, числа с плавающей запятой часто определяются как целые числа, умноженные на положительную или отрицательную степень двойки. Числа, которые могут быть точно представлены в формате с плавающей запятой, например типы данных с плавающей запятой IEEE , называются представимыми числами. Для большинства представлений с плавающей запятой представимые числа являются подмножеством диадических рациональных чисел. ^[6] То же самое справедливо и для типов данных с фиксированной точкой , которые в большинстве случаев также неявно используют степени двойки. ^[7] Из-за простоты вычислений с двоичными рациональными числами они также используются для точных реальных вычислений с использованием интервальной арифметики . ^[8] и являются центральными в некоторых теоретических моделях вычислимых чисел . ^[9]^[10]^[11]

Генерация случайной величины из случайных битов за фиксированный промежуток времени возможна только в том случае, если переменная имеет конечное число результатов, вероятности которых все являются двоично-рациональными числами. Для случайных величин, вероятности которых не являются двоичными, необходимо либо аппроксимировать их вероятности двоично-рациональными числами, либо использовать процесс случайной генерации, время которого само по себе случайно и неограниченно. ^[12]

В музыке

${ \new PianoStaff << \new Staff \relative c'' { \set Staff.midiInstrument = #"violin" \ скрипичный ключ \tempo 8 = 126 \time 3/16 r16 <dca fis d>\f-! r16\фермата | \time 2/16 r <dca fis d>-! \time 3/16 r <dca fis d>8-! | r16 <dca fis d>8-! | \time 2/8 <dca fis>16-! <ec bes g>->-![ <cis b aes f>-! <ca fis ees>-!] } \new Staff \relative c { \set Staff.midiInstrument = #"violin" \clef bass \time 3/16 d,16-! <бес''ееес,>-! р\фермата | \время 2/16 <д,, д,>-! <бес''ееес,>-! | \время 16 марта d16-! <ees цис>8-! | r16 <ees cis>8-! | \время 2/8 д16\сф-! <ees cis>-!->[ <d c>-! <d c>-!] } >> }$

Пять тактов из Игоря Стравинского оперы «Весна священная»
показ тактовых размеров ³
₁₆, ²
₁₆, ³
₁₆ и ²
₈

Тактовые размеры в западной нотной записи традиционно записываются в форме, напоминающей дроби (например: ²
₂, ⁴
₄ или ⁶
₈), ^[13] хотя горизонтальная линия нотного нотоносца, разделяющая верхнюю и нижнюю цифру, обычно опускается при написании подписи отдельно от нотного стана. Как дроби они обычно диадические, ^[14] хотя недиадические размеры . также использовались ^[15] Числовое значение подписи, интерпретируемое как дробь, описывает длину такта как долю целой ноты . Его числитель описывает количество долей на такт, а знаменатель описывает длину каждой доли. ^[13]^[14]

По математическому образованию

В теориях детского развития понятия дроби, основанных на работах Жана Пиаже , дробные числа, возникающие в результате деления пополам и повторного деления пополам, являются одними из самых ранних форм развития дробей. ^[16] Этот этап развития понятия дробей получил название «алгоритмическое сокращение пополам». ^[17] Сложение и вычитание этих чисел можно выполнять поэтапно, включая удвоение, деление пополам, сложение и вычитание целых чисел. Напротив, сложение и вычитание более общих дробей включает в себя целочисленное умножение и факторизацию для достижения общего знаменателя. Таким образом, учащимся легче вычислять двоичные дроби, чем более общие дроби. ^[18]

Определения и арифметика

Диадические числа — это рациональные числа , которые получаются в результате деления целого числа на степень двойки . ^[9] Рациональное число $p/q$ Проще говоря, является двоично-рациональным, когда $q$ это степень двойки. ^[19] Другой эквивалентный способ определения двоичных рациональных чисел состоит в том, что они представляют собой действительные числа , имеющие завершающее двоичное представление . ^[9]

Сложение , вычитание и умножение любых двух двоичных рациональных чисел дает другое двоичное рациональное число в соответствии со следующими формулами: ^[20]

{\begin{aligned}{\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}&={\frac {2^{d-\min(b,d)}a+2^{b-\min(b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}&={\frac {2^{d-\min(b,d)}a-2^{b-\min(b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{2^{b}}}\cdot {\frac {c}{2^{d}}}&={\frac {ac}{2^{b+d}}}\end{aligned}}

Однако результат деления одного двоичного рационального на другой не обязательно является двоично-рациональным. ^[21] Например, 1 и 3 — двоично-рациональные числа, а 1/3 — нет.

Дополнительные свойства

Каждое целое число и каждое полуцелое число являются двоично-рациональными. ^[22] Оба они соответствуют определению целого числа, разделенного на степень двойки: каждое целое число — это целое число, разделенное на единицу (нулевая степень двойки), а каждое полуцелое число — это целое число, разделенное на два.

Каждое действительное число может быть сколь угодно близко аппроксимировано двоичными рациональными числами. В частности, для действительного числа $x$ , рассмотрим двоично-рациональные числа вида ${\textstyle \lfloor 2^{i}x\rfloor /2^{i}}$ , где $i$ может быть любым целым числом и $\lfloor \dots \rfloor$ обозначает функцию пола , которая округляет свой аргумент до целого числа. Эти цифры приблизительны $x$ снизу с точностью до ошибки $1/2^{i}$ , которую можно сделать сколь угодно малой, выбрав $i$ быть сколь угодно большим. Для фрактального подмножества действительных чисел эта граница ошибки находится в пределах постоянного коэффициента оптимальности: для этих чисел не существует аппроксимации. $n/2^{i}$ с ошибкой меньше постоянного раза $1/2^{i}$ . ^[23]^[24] Существование точных двоичных приближений можно выразить, сказав, что множество всех двоичных рациональных чисел плотно в действительной прямой . ^[22] Более строго, это множество равномерно плотно в том смысле, что двоично-рациональные числа со знаменателем $2^{i}$ расположены равномерно на действительной прямой. ^[9]

Двоичные рациональные числа — это именно те числа, которые обладают конечными двоичными разложениями . ^[9] Их двоичные расширения не уникальны; существует одно конечное и одно бесконечное представление каждого двоично-рационального, отличного от 0 (игнорируя терминальные 0). Например, 0.11 ₂ = 0.10111... ₂ , что дает два разных представления для 3/4. ^[9]^[25] Двоичные рациональные числа — единственные числа, двоичные представления которых не уникальны. ^[9]

В высшей математике

Алгебраическая структура

Поскольку двоичные рациональные числа замкнуты относительно сложения, вычитания и умножения, но не деления, они представляют собой кольцо , а не поле . ^[26] Кольцо двоичных рациональных чисел можно обозначить $\mathbb {Z} [{\tfrac {1}{2}}]$ , что означает, что его можно сгенерировать путем оценки полиномов с целыми коэффициентами с аргументом 1/2. ^[27] Как кольцо, двоичные рациональные числа представляют собой подкольцо рациональных чисел и надкольцо целых чисел. ^[28] Алгебраически это кольцо представляет собой локализацию целых чисел относительно множества степеней двойки . ^[29]

Двоичные рациональные числа не только образуют подкольцо действительных чисел , но и образуют подкольцо 2-адических чисел — систему чисел, которая может быть определена из двоичных представлений, которые конечны справа от двоичной точки, но могут расширяться бесконечно. далеко слева. К 2-адическим числам относятся все рациональные числа, а не только двоично-рациональные. Встраивание двоичных рациональных чисел в 2-адические числа не меняет арифметику двоичных рациональных чисел, но придает им топологическую структуру, отличную от той, которую они имеют в качестве подкольца действительных чисел. Как и в реальных числах, двоично-рациональные числа образуют плотное подмножество 2-адических чисел, ^[30] и являются множеством 2-адических чисел с конечными двоичными разложениями. Каждое 2-адическое число можно разложить в сумму 2-адического целого числа и двоично-рационального числа; в этом смысле двоичные рациональные числа могут представлять дробные части 2-адических чисел, но это разложение не уникально. ^[31]

Сложение двоичных рациональных чисел по модулю 1 ( фактор-группа $\mathbb {Z} [{\tfrac {1}{2}}]/\mathbb {Z}$ двоичных рациональных чисел целыми числами) образует 2-группу Прюфера . ^[32]

Двойной соленоид

Рассмотрение только операций сложения и вычитания двоичных рациональных чисел дает им структуру аддитивной абелевой группы . Двойственность Понтрягина — это метод понимания абелевых групп путем построения двойственных групп, элементы которых являются характерами исходной группы, групповых гомоморфизмов мультипликативной группы комплексных чисел с поточечным умножением в качестве операции двойственной группы. Построенную таким образом двойственную группу аддитивных диадических рациональных чисел также можно рассматривать как топологическую группу . Он называется диадическим соленоидом и изоморфен топологическому произведению действительных чисел и 2-адических чисел, факторизованному диагональным вложением двоично-рациональных чисел в это произведение. ^[30] Это пример протора , соленоида и неразложимого континуума . ^[33]

Функции с двоично-рациональными числами в качестве выделенных точек

Функция вопросительного знака Минковского отображает рациональные числа в двоично-рациональные числа.

График масштабирующих и вейвлет-функций вейвлета Добеши

Вейвлет Добеши , показывающий точки негладкости в диадических рациональных числах.

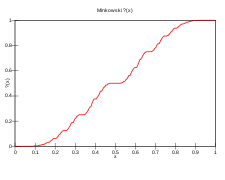
Поскольку они представляют собой плотное подмножество действительных чисел, диадические рациональные числа с их числовым порядком образуют плотный порядок . Как и в случае любых двух неограниченных счетных плотных линейных порядков, по теореме Кантора об изоморфизме , ^[34] двоичные рациональные числа по порядку изоморфны рациональным числам. В этом случае функция вопросительного знака Минковского обеспечивает сохраняющую порядок биекцию между множеством всех рациональных чисел и множеством двоичных рациональных чисел. ^[35]

Диадические рациональные числа играют ключевую роль в анализе вейвлетов Добеши как набора точек, в которых функция масштабирования этих вейвлетов не является гладкой. ^[26] Точно так же двоичные рациональные числа параметризуют разрывы на границе между стабильными и неустойчивыми точками в пространстве параметров отображения Энона . ^[36]

Набор кусочно-линейных гомеоморфизмов из единичного интервала в себя, которые имеют наклоны степени 2 и двоично-рациональные точки излома, образует группу при операции композиции функций . Это группа Томпсона , первый известный пример бесконечной, но конечно представленной простой группы . ^[37] Эту же группу можно представить действием над корневыми двоичными деревьями: ^[38] или действием на двоичные рациональные числа в пределах единичного интервала. ^[32]

Другие сопутствующие конструкции

В обратной математике один из способов построения действительных чисел состоит в том, чтобы представить их как функции от унарных чисел до двоичных рациональных чисел, где значение одной из этих функций для аргумента $i$ является двоично-рациональным числом со знаменателем $2^{i}$ которое приближает данное действительное число. Такое определение действительных чисел позволяет многие основные результаты математического анализа доказать в рамках ограниченной теории арифметики второго порядка, называемой «выполнимый анализ» (BTFA). ^[39]

Сюрреалистические числа генерируются с помощью повторяющегося принципа построения, который начинается с генерации всех конечных двоичных рациональных чисел, а затем переходит к созданию новых и странных видов бесконечных, бесконечно малых и других чисел. ^[40] Эта система счисления является основой комбинаторной теории игр , и диадические рациональные числа естественным образом возникают в этой теории как набор значений определенных комбинаторных игр. ^[41]^[42]^[19]

Плавкие числа - это подмножество двоично-рациональных чисел, замыкание множества $\{0\}$ под операцией $x,y\mapsto (x+y+1)/2$ , ограничено парами $x,y$ с $|x-y|<1$ . Они хорошо упорядочены , тип порядка равен числу эпсилон. $\varepsilon _{0}$ . Для каждого целого числа $n$ наименьшее плавкое число, большее $n$ имеет форму $n+1/2^{k}$ . Существование $k$ для каждого $n$ невозможно доказать с помощью арифметики Пеано , ^[43] и $k$ растет так быстро в зависимости от $n$ это для $n=3$ оно (в обозначениях Кнута со стрелкой вверх для больших чисел) уже больше, чем $2\uparrow ^{9}16$ . ^[44]

Обычное доказательство леммы Урысона использует двоичные дроби для построения разделяющей функции из леммы.

Ссылки

^ Рудман, Питер С. (2009), Как возникла математика: первые 50 000 лет , Prometheus Books, стр. 148, ISBN 978-1-61592-176-8
^ Барнс, Джон (2016), Nice Numbers , Springer International Publishing, номер документа : 10.1007/978-3-319-46831-0 , ISBN 978-3-319-46830-3 , Обратите внимание, что бинарные меры (2, 4, 8, 16) действительно очень распространены. Это особенно очевидно на объемах.
^ Кертис, Лоренцо Дж. (1978), «Концепция экспоненциального закона до 1900 года», American Journal of Physics , 46 (9): 896–906, Бибкод : 1978AmJPh..46..896C , doi : 10.1119/1.11512
^ Миллер, Хизер М.-Л. (2013), «Веские вопросы: свидетельства единства и регионального разнообразия на основе веса цивилизации Инда», у Авраама, Шину Анна; Гуллапалли, Правина; Рачек, Тереза П.; Ризви, Узма З. (ред.), Связи и сложность: новые подходы к археологии Южной Азии , Left Coast Press, стр. 161–177, doi : 10.4324/9781315431857 , ISBN 978-1-59874-686-0 ; см., в частности, стр. 166
^ Резников, Ховард Л .; Уэллс, Раймонд О. младший (1998), «2.2.1: Цифровые компьютеры и измерения» , Вейвлет-анализ: масштабируемая структура информации , Нью-Йорк: Springer-Verlag, стр. 17–18, doi : 10.1007/978- 1-4612-0593-7 , ISBN 0-387-98383-Х , МР 1712468
^ Кирк, Дэвид Б .; Хву, Вэнь-мэй В. (2013), «7.2 Представленные числа» , Программирование массово-параллельных процессоров: практический подход (2-е изд.), Морган Кауфманн, стр. 155–159, ISBN 978-0-12-391418-7
^ Кнейзель, Рональд Т. (2017), «Глава 6: Числа с фиксированной точкой», Числа и компьютеры (2-е изд.), Springer International Publishing, стр. 183–214, doi : 10.1007/978-3-319-50508- 4_6
^ ван дер Хувен, Йорис (2006), «Вычисления с эффективными действительными числами», Theoretical Computer Science , 351 (1): 52–60, doi : 10.1016/j.tcs.2005.09.060 , MR 2201092
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г Ко, Кер-И (1991), Теория сложности действительных функций , Прогресс в теоретической информатике, Бостон, Массачусетс: Birkhäuser Boston, Inc., стр. 41–43, номер документа : 10.1007/978-1-4684-6802-1 , ISBN 0-8176-3586-6 , МР 1137517 , S2CID 11758381
^ Чжэн, Сичжун; Реттингер, Роберт (2004), «Слабая вычислимость и представление действительных чисел», Mathematical Logic Quarterly , 50 (4–5): 431–442, doi : 10.1002/malq.200310110 , MR 2090389 , S2CID 15815720
^ Амбос-Спис, Клаус; Чжэн, Сичжун (2019), «О разностях и суммах сильно вычислимых действительных чисел», в Манеа, Флорин; Мартин, Барнаби; Паулюсма, Даниэль; Примьеро, Джузеппе (ред.), Вычисления с прогнозированием и промышленностью: 15-я конференция по вычислительности в Европе, CiE 2019, Дарем, Великобритания, 15–19 июля 2019 г., Материалы , конспекты лекций по информатике, том. 11558, Чам: Спрингер, стр. 310–322, doi : 10.1007/978-3-030-22996-2_27 , MR 3981892 , S2CID 195795492 .
^ Джеррам, Марк Р .; Валиант, Лесли Г .; Вазирани, Виджай В. (1986), «Случайная генерация комбинаторных структур из равномерного распределения», Theoretical Computer Science , 43 (2–3): 169–188, doi : 10.1016/0304-3975(86)90174-X , МР 0855970
^ Jump up to: ^а ^б Джонс, Шелли М .; Пирсон, Данн (май 2013 г.), «Музыка: увлеченные студенты соединяют музыку с математикой», General Music Today , 27 (1): 18–23, doi : 10.1177/1048371313486478 , S2CID 220604326
^ Jump up to: ^а ^б Либби, Теодор (2006), «Тактовый размер» , Энциклопедия классической музыки для слушателей NPR , Workman Publishing, стр. 873, ISBN 978-0-7611-2072-8
^ Янакиев, Иван К. (2020), «Математические приемы в помощь теории музыки, композиции и исполнению», в Божиковой, Милене (редактор), Музыка между онтологией и идеологией , Cambridge Scholars Publishing, стр. 35–62, ISBN 978-1-5275-4758-2 ; см., в частности, стр. 37 .
^ Хиберт, Джеймс; Тоннессен, Лоуэлл Х. (ноябрь 1978 г.), «Развитие концепции дроби в двух физических контекстах: предварительное исследование», Journal for Research in Mathematics Education , 9 (5): 374–378, doi : 10.2307/748774 , JSTOR 748774
^ Потье, Ивонн ; Савада, Дайо (ноябрь 1983 г.), «Разделение: появление идей рациональных чисел у маленьких детей», Journal for Research in Mathematics Education , 14 (5): 307–317, doi : 10.2307/748675 , JSTOR 748675
^ Уэллс, Дэвид Грэм (2015), Мотивирующая математика: вовлечение учителей и вовлеченных студентов , World Scientific, стр. 32–33, ISBN 978-1-78326-755-2
^ Jump up to: ^а ^б Уитервейк, Йос WHM; Бартон, Майкл (2015), «Новые результаты для доминирования из баз данных эндшпиля комбинаторной теории игр», Theoretical Computer Science , 592 : 72–86, arXiv : 1506.03949 , doi : 10.1016/j.tcs.2015.05.017 , MR 3367582 , S2CID 5899577
^ Эквивалентные им формулы, написанные на языке интерактивного средства доказательства теорем Coq , имеют вид Кребберс, Робберт; Спиттерс, Бас (2013), «Классы типов для эффективной точной вещественной арифметики в Coq», Logical Methods in Computer Science , 9 (1): 1:01, 27, arXiv : 1106.3448 , doi : 10.2168/LMCS-9(1: 1)2013 , МР 3029087 , S2CID 218627153
^ О'Коннор, Рассел (2007), «Монадическая функциональная реализация действительных чисел», Mathematical Structures in Computer Science , 17 (1): 129–159, arXiv : cs/0605058 , doi : 10.1017/S0960129506005871 , MR 2311089 , S2CID 221168970
^ Jump up to: ^а ^б Сабин, Малкольм (2010), Анализ и проектирование одномерных схем подразделения , Геометрия и вычисления, том. 6, Спрингер, с. 51, ISBN 9783642136481
^ Точнее, для малых положительных значений $\varepsilon$ , набор действительных чисел, не имеющих приближения $n/2^{i}$ с ошибкой меньше постоянного раза $\varepsilon /2^{i}$ образует канторово множество которого , размерность по Хаусдорфу , как функция $\varepsilon$ , переходит к одному как $\varepsilon$ приближается к нулю. На рисунке показан этот набор для $\varepsilon ={\tfrac {1}{6}}$ .
^ Нильссон, Йохан (2009), «О числах, плохо аппроксимируемых диадическими рациональными числами», Израильский математический журнал , 171 : 93–110, doi : 10.1007/s11856-009-0042-9 , MR 2520103
^ Кац, Марк (1959), Статистическая независимость в теории вероятностей, анализе и теории чисел , Carus Mathematical Monographs , vol. 12, Нью-Йорк: John Wiley & Sons для Математической ассоциации Америки, стр. 2–3, MR 0110114.
^ Jump up to: ^а ^б Поллен, Дэвид (1992), «Масштабирующая функция Добеши на [0,3]», Вейвлеты , Вейвлет-анализ и его приложения, том. 2, Бостон, Массачусетс: Academic Press, стр. 3–13, MR 1161245.
^ Байнок, Бела (2013), Приглашение к абстрактной математике , Тексты для бакалавров по математике, Нью-Йорк: Springer, стр. 186, номер домена : 10.1007/978-1-4614-6636-9 , ISBN. 978-1-4614-6635-2
^ В обозначениях Эстеса и Ома для колец, которые являются подкольцами $\mathbb {Q}$ и перевороты $\mathbb {Z}$ , двоично-рациональные числа - это кольцо $\mathbb {Z} _{\{2\}}$ . См. раздел 7 Эстес, Деннис; Ом, Джек (1967), «Стабильный диапазон в коммутативных кольцах» (PDF) , Journal of Algebra , 7 (3): 343–362, doi : 10.1016/0021-8693(67)90075-0 , MR 0217052
^ Люсишин-Райт, Рори Б.Б. (2018), «Выпуклые пространства, аффинные пространства и коммутанты для алгебраических теорий», Applied Categorical Structures , 26 (2): 369–400, arXiv : 1603.03351 , doi : 10.1007/s10485-017-9496 -9 , МР 3770912 , S2CID 3743682
^ Jump up to: ^а ^б Маннерс, Фредди (2015), «Решение проблемы с пижамой», Inventiones Mathematicae , 202 (1): 239–270, arXiv : 1305.1514 , Bibcode : 2015InMat.202..239M , doi : 10.1007/s00222-014-0571 -7 , МР 3402799 , S2CID 119148680 ; см. раздел 6.2.1, «Типовой случай: ${\widehat {\mathbb {Z} [1/2]}}$ ", стр. 255–257.
^ Роберт, Ален М. (2000), «5.4 Дробные и целые части $p$ -адические числа», Курс $p$ -адический анализ , Тексты для аспирантов по математике , вып. 198, Нью-Йорк: Springer-Verlag, стр. 40–43, doi : 10.1007/978-1-4757-3254-2 , ISBN. 0-387-98669-3 , МР 1760253
^ Jump up to: ^а ^б де Корнюлье, Ив; Гайо, Люк; Питч, Вольфганг (2007), «Об изолированных точках в пространстве групп» (PDF) , Journal of Algebra , 307 (1): 254–277, arXiv : math/0511714 , doi : 10.1016/j.jalgebra.2006.02 .012 , МР 2278053 , S2CID 11566447
^ Надлер, С.Б. младший (1973), «Неразложимость диадического соленоида», The American Mathematical Monthly , 80 (6): 677–679, doi : 10.2307/2319174 , JSTOR 2319174
^ Бхаттачарджи, Минакси; Макферсон, Дугалд; Мёллер, Рёнвальдур Г.; Нойманн, Питер М. (1997), «Рациональные числа», Заметки о бесконечных группах перестановок , Тексты и материалы для чтения по математике, том. 12, Берлин: Springer-Verlag, стр. 77–86, номер документа : 10.1007/978-93-80250-91-5_9 , ISBN. 81-85931-13-5 , МР 1632579
^ Гиргенсон, Роланд (1996), «Построение сингулярных функций с помощью дробей Фарея», Журнал математического анализа и приложений , 203 (1): 127–141, doi : 10.1006/jmaa.1996.0370 , MR 1412484
^ Цвитанович, Предраг; Гунаратне, Гемуну Х.; Прокачча, Итамар (1988), «Топологические и метрические свойства странных аттракторов типа Энона», Physical Review A , Third Series, 38 (3): 1503–1520, Бибкод : 1988PhRvA..38.1503C , doi : 10.1103/PhysRevA. 38.1503 , МР 0970237 , ПМИД 9900529
^ Брин, Мэтью Г. (1999), «Повсеместность группы Томпсона $F$ в группах кусочно-линейных гомеоморфизмов единичного интервала», Журнал Лондонского математического общества , вторая серия, 60 (2): 449–460, arXiv : математика /9705205 , doi : 10.1112/S0024610799007905 , MR 1724861 , S2CID 14490692
^ Кэннон, JW ; Флойд, WJ (2011), «Что такое… группа Томпсона?» (PDF) , Уведомления Американского математического общества , 58 (8): 1112–1113, MR 2856142.
^ Фернандес, Антониу М.; Феррейра, Фернандо (2005), «Основные применения слабой леммы Кенига в осуществимом анализе» (PDF) , Обратная математика 2001 , Конспекты лекций по логике, том. 21, Ла-Хойя, Калифорния: Ассоциация символической логики, стр. 175–188, MR 2185433.
^ Конвей, Дж. Х. (2001), О числах и играх (второе изд.), Натик, Массачусетс: AK Peters, ISBN 1-56881-127-6 , МР 1803095 ; о диадических рациональных числах см. «Числа ${\tfrac {1}{4}}$ , ${\tfrac {3}{4}}$ , $1\,{\tfrac {1}{2}}$ , $3$ и так далее», стр. 10–12.
^ Молдон, Дж. Г. (1978), «Нум, вариант Нима без победы первого игрока», The American Mathematical Monthly , 85 (7): 575–578, doi : 10.2307/2320870 , JSTOR 2320870 , MR 0503877
^ Фланиган, Дж. А. (1982), «Полный анализ черно-белых хакендотов», Международный журнал теории игр , 11 (1): 21–25, doi : 10.1007/BF01771244 , MR 0665515 , S2CID 119964871
^ Эриксон, Джефф; Ниваш, Габриэль; Сюй, Цзюньян (июнь 2021 г.), «Плавкие числа и арифметика Пеано» , Труды 36-го ежегодного симпозиума ACM/IEEE по логике в информатике (LICS 2021) , IEEE, стр. 1–13, arXiv : 2003.14342 , doi : 10.1109 /lics52264.2021.9470703 , S2CID 214727767
^ Слоан, Нью-Джерси (редактор), «Последовательность A188545» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS

[rudman-1] Рудман, Питер С. (2009), Как возникла математика: первые 50 000 лет , Prometheus Books, стр. 148, ISBN 978-1-61592-176-8

[barnes-2] Барнс, Джон (2016), Nice Numbers , Springer International Publishing, номер документа : 10.1007/978-3-319-46831-0 , ISBN 978-3-319-46830-3 , Обратите внимание, что бинарные меры (2, 4, 8, 16) действительно очень распространены. Это особенно очевидно на объемах.

[curtis-3] Кертис, Лоренцо Дж. (1978), «Концепция экспоненциального закона до 1900 года», American Journal of Physics , 46 (9): 896–906, Бибкод : 1978AmJPh..46..896C , doi : 10.1119/1.11512

[miller-4] Миллер, Хизер М.-Л. (2013), «Веские вопросы: свидетельства единства и регионального разнообразия на основе веса цивилизации Инда», у Авраама, Шину Анна; Гуллапалли, Правина; Рачек, Тереза П.; Ризви, Узма З. (ред.), Связи и сложность: новые подходы к археологии Южной Азии , Left Coast Press, стр. 161–177, doi : 10.4324/9781315431857 , ISBN 978-1-59874-686-0 ; см., в частности, стр. 166

[reswel-5] Резников, Ховард Л .; Уэллс, Раймонд О. младший (1998), «2.2.1: Цифровые компьютеры и измерения» , Вейвлет-анализ: масштабируемая структура информации , Нью-Йорк: Springer-Verlag, стр. 17–18, doi : 10.1007/978- 1-4612-0593-7 , ISBN 0-387-98383-Х , МР 1712468

[kirk-hwu-6] Кирк, Дэвид Б .; Хву, Вэнь-мэй В. (2013), «7.2 Представленные числа» , Программирование массово-параллельных процессоров: практический подход (2-е изд.), Морган Кауфманн, стр. 155–159, ISBN 978-0-12-391418-7

[kneusel-7] Кнейзель, Рональд Т. (2017), «Глава 6: Числа с фиксированной точкой», Числа и компьютеры (2-е изд.), Springer International Publishing, стр. 183–214, doi : 10.1007/978-3-319-50508- 4_6

[vdh-8] ван дер Хувен, Йорис (2006), «Вычисления с эффективными действительными числами», Theoretical Computer Science , 351 (1): 52–60, doi : 10.1016/j.tcs.2005.09.060 , MR 2201092

[ko-9] Jump up to: ^а ^б ^с ^д ^и ^ж ^г Ко, Кер-И (1991), Теория сложности действительных функций , Прогресс в теоретической информатике, Бостон, Массачусетс: Birkhäuser Boston, Inc., стр. 41–43, номер документа : 10.1007/978-1-4684-6802-1 , ISBN 0-8176-3586-6 , МР 1137517 , S2CID 11758381

[zr-10] Чжэн, Сичжун; Реттингер, Роберт (2004), «Слабая вычислимость и представление действительных чисел», Mathematical Logic Quarterly , 50 (4–5): 431–442, doi : 10.1002/malq.200310110 , MR 2090389 , S2CID 15815720

[asz-11] Амбос-Спис, Клаус; Чжэн, Сичжун (2019), «О разностях и суммах сильно вычислимых действительных чисел», в Манеа, Флорин; Мартин, Барнаби; Паулюсма, Даниэль; Примьеро, Джузеппе (ред.), Вычисления с прогнозированием и промышленностью: 15-я конференция по вычислительности в Европе, CiE 2019, Дарем, Великобритания, 15–19 июля 2019 г., Материалы , конспекты лекций по информатике, том. 11558, Чам: Спрингер, стр. 310–322, doi : 10.1007/978-3-030-22996-2_27 , MR 3981892 , S2CID 195795492 .

[jvv-12] Джеррам, Марк Р .; Валиант, Лесли Г .; Вазирани, Виджай В. (1986), «Случайная генерация комбинаторных структур из равномерного распределения», Theoretical Computer Science , 43 (2–3): 169–188, doi : 10.1016/0304-3975(86)90174-X , МР 0855970

[jon-pea-13] Jump up to: ^а ^б Джонс, Шелли М .; Пирсон, Данн (май 2013 г.), «Музыка: увлеченные студенты соединяют музыку с математикой», General Music Today , 27 (1): 18–23, doi : 10.1177/1048371313486478 , S2CID 220604326

[libbey-14] Jump up to: ^а ^б Либби, Теодор (2006), «Тактовый размер» , Энциклопедия классической музыки для слушателей NPR , Workman Publishing, стр. 873, ISBN 978-0-7611-2072-8

[yanakiev-15] Янакиев, Иван К. (2020), «Математические приемы в помощь теории музыки, композиции и исполнению», в Божиковой, Милене (редактор), Музыка между онтологией и идеологией , Cambridge Scholars Publishing, стр. 35–62, ISBN 978-1-5275-4758-2 ; см., в частности, стр. 37 .

[hie-ton-16] Хиберт, Джеймс; Тоннессен, Лоуэлл Х. (ноябрь 1978 г.), «Развитие концепции дроби в двух физических контекстах: предварительное исследование», Journal for Research in Mathematics Education , 9 (5): 374–378, doi : 10.2307/748774 , JSTOR 748774

[pot-saw-17] Потье, Ивонн ; Савада, Дайо (ноябрь 1983 г.), «Разделение: появление идей рациональных чисел у маленьких детей», Journal for Research in Mathematics Education , 14 (5): 307–317, doi : 10.2307/748675 , JSTOR 748675

[wells-18] Уэллс, Дэвид Грэм (2015), Мотивирующая математика: вовлечение учителей и вовлеченных студентов , World Scientific, стр. 32–33, ISBN 978-1-78326-755-2

[uit-bar-19] Jump up to: ^а ^б Уитервейк, Йос WHM; Бартон, Майкл (2015), «Новые результаты для доминирования из баз данных эндшпиля комбинаторной теории игр», Theoretical Computer Science , 592 : 72–86, arXiv : 1506.03949 , doi : 10.1016/j.tcs.2015.05.017 , MR 3367582 , S2CID 5899577

[kreb-spit-20] Эквивалентные им формулы, написанные на языке интерактивного средства доказательства теорем Coq , имеют вид Кребберс, Робберт; Спиттерс, Бас (2013), «Классы типов для эффективной точной вещественной арифметики в Coq», Logical Methods in Computer Science , 9 (1): 1:01, 27, arXiv : 1106.3448 , doi : 10.2168/LMCS-9(1: 1)2013 , МР 3029087 , S2CID 218627153

[oconnor-21] О'Коннор, Рассел (2007), «Монадическая функциональная реализация действительных чисел», Mathematical Structures in Computer Science , 17 (1): 129–159, arXiv : cs/0605058 , doi : 10.1017/S0960129506005871 , MR 2311089 , S2CID 221168970

[sabin-22] Jump up to: ^а ^б Сабин, Малкольм (2010), Анализ и проектирование одномерных схем подразделения , Геометрия и вычисления, том. 6, Спрингер, с. 51, ISBN 9783642136481

[23] Точнее, для малых положительных значений $\varepsilon$ , набор действительных чисел, не имеющих приближения $n/2^{i}$ с ошибкой меньше постоянного раза $\varepsilon /2^{i}$ образует канторово множество которого , размерность по Хаусдорфу , как функция $\varepsilon$ , переходит к одному как $\varepsilon$ приближается к нулю. На рисунке показан этот набор для $\varepsilon ={\tfrac {1}{6}}$ .

[nilsson-24] Нильссон, Йохан (2009), «О числах, плохо аппроксимируемых диадическими рациональными числами», Израильский математический журнал , 171 : 93–110, doi : 10.1007/s11856-009-0042-9 , MR 2520103

[kac-25] Кац, Марк (1959), Статистическая независимость в теории вероятностей, анализе и теории чисел , Carus Mathematical Monographs , vol. 12, Нью-Йорк: John Wiley & Sons для Математической ассоциации Америки, стр. 2–3, MR 0110114.

[pollen-26] Jump up to: ^а ^б Поллен, Дэвид (1992), «Масштабирующая функция Добеши на [0,3]», Вейвлеты , Вейвлет-анализ и его приложения, том. 2, Бостон, Массачусетс: Academic Press, стр. 3–13, MR 1161245.

[bajnok-27] Байнок, Бела (2013), Приглашение к абстрактной математике , Тексты для бакалавров по математике, Нью-Йорк: Springer, стр. 186, номер домена : 10.1007/978-1-4614-6636-9 , ISBN. 978-1-4614-6635-2

[est-ohm-28] В обозначениях Эстеса и Ома для колец, которые являются подкольцами $\mathbb {Q}$ и перевороты $\mathbb {Z}$ , двоично-рациональные числа - это кольцо $\mathbb {Z} _{\{2\}}$ . См. раздел 7 Эстес, Деннис; Ом, Джек (1967), «Стабильный диапазон в коммутативных кольцах» (PDF) , Journal of Algebra , 7 (3): 343–362, doi : 10.1016/0021-8693(67)90075-0 , MR 0217052

[lucy-29] Люсишин-Райт, Рори Б.Б. (2018), «Выпуклые пространства, аффинные пространства и коммутанты для алгебраических теорий», Applied Categorical Structures , 26 (2): 369–400, arXiv : 1603.03351 , doi : 10.1007/s10485-017-9496 -9 , МР 3770912 , S2CID 3743682

[manners-30] Jump up to: ^а ^б Маннерс, Фредди (2015), «Решение проблемы с пижамой», Inventiones Mathematicae , 202 (1): 239–270, arXiv : 1305.1514 , Bibcode : 2015InMat.202..239M , doi : 10.1007/s00222-014-0571 -7 , МР 3402799 , S2CID 119148680 ; см. раздел 6.2.1, «Типовой случай: ${\widehat {\mathbb {Z} [1/2]}}$ ", стр. 255–257.

[robert-31] Роберт, Ален М. (2000), «5.4 Дробные и целые части $p$ -адические числа», Курс $p$ -адический анализ , Тексты для аспирантов по математике , вып. 198, Нью-Йорк: Springer-Verlag, стр. 40–43, doi : 10.1007/978-1-4757-3254-2 , ISBN. 0-387-98669-3 , МР 1760253

[cor-guy-pit-32] Jump up to: ^а ^б де Корнюлье, Ив; Гайо, Люк; Питч, Вольфганг (2007), «Об изолированных точках в пространстве групп» (PDF) , Journal of Algebra , 307 (1): 254–277, arXiv : math/0511714 , doi : 10.1016/j.jalgebra.2006.02 .012 , МР 2278053 , S2CID 11566447

[nadler-33] Надлер, С.Б. младший (1973), «Неразложимость диадического соленоида», The American Mathematical Monthly , 80 (6): 677–679, doi : 10.2307/2319174 , JSTOR 2319174

[bmmn-34] Бхаттачарджи, Минакси; Макферсон, Дугалд; Мёллер, Рёнвальдур Г.; Нойманн, Питер М. (1997), «Рациональные числа», Заметки о бесконечных группах перестановок , Тексты и материалы для чтения по математике, том. 12, Берлин: Springer-Verlag, стр. 77–86, номер документа : 10.1007/978-93-80250-91-5_9 , ISBN. 81-85931-13-5 , МР 1632579

[girgensohn-35] Гиргенсон, Роланд (1996), «Построение сингулярных функций с помощью дробей Фарея», Журнал математического анализа и приложений , 203 (1): 127–141, doi : 10.1006/jmaa.1996.0370 , MR 1412484

[cvi-gun-pro-36] Цвитанович, Предраг; Гунаратне, Гемуну Х.; Прокачча, Итамар (1988), «Топологические и метрические свойства странных аттракторов типа Энона», Physical Review A , Third Series, 38 (3): 1503–1520, Бибкод : 1988PhRvA..38.1503C , doi : 10.1103/PhysRevA. 38.1503 , МР 0970237 , ПМИД 9900529

[brin-37] Брин, Мэтью Г. (1999), «Повсеместность группы Томпсона $F$ в группах кусочно-линейных гомеоморфизмов единичного интервала», Журнал Лондонского математического общества , вторая серия, 60 (2): 449–460, arXiv : математика /9705205 , doi : 10.1112/S0024610799007905 , MR 1724861 , S2CID 14490692

[can-flo-38] Кэннон, JW ; Флойд, WJ (2011), «Что такое… группа Томпсона?» (PDF) , Уведомления Американского математического общества , 58 (8): 1112–1113, MR 2856142.

[fer-fer-39] Фернандес, Антониу М.; Феррейра, Фернандо (2005), «Основные применения слабой леммы Кенига в осуществимом анализе» (PDF) , Обратная математика 2001 , Конспекты лекций по логике, том. 21, Ла-Хойя, Калифорния: Ассоциация символической логики, стр. 175–188, MR 2185433.

[conway-40] Конвей, Дж. Х. (2001), О числах и играх (второе изд.), Натик, Массачусетс: AK Peters, ISBN 1-56881-127-6 , МР 1803095 ; о диадических рациональных числах см. «Числа ${\tfrac {1}{4}}$ , ${\tfrac {3}{4}}$ , $1\,{\tfrac {1}{2}}$ , $3$ и так далее», стр. 10–12.

[mauldon-41] Молдон, Дж. Г. (1978), «Нум, вариант Нима без победы первого игрока», The American Mathematical Monthly , 85 (7): 575–578, doi : 10.2307/2320870 , JSTOR 2320870 , MR 0503877

[flanigan-42] Фланиган, Дж. А. (1982), «Полный анализ черно-белых хакендотов», Международный журнал теории игр , 11 (1): 21–25, doi : 10.1007/BF01771244 , MR 0665515 , S2CID 119964871

[eri-niv-xu-43] Эриксон, Джефф; Ниваш, Габриэль; Сюй, Цзюньян (июнь 2021 г.), «Плавкие числа и арифметика Пеано» , Труды 36-го ежегодного симпозиума ACM/IEEE по логике в информатике (LICS 2021) , IEEE, стр. 1–13, arXiv : 2003.14342 , doi : 10.1109 /lics52264.2021.9470703 , S2CID 214727767

[A188545-44] Слоан, Нью-Джерси (редактор), «Последовательность A188545» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

v т и Дроби и соотношения
	Division and ratio	Dividend ÷ Divisor = Quotient
	Fraction	⁠Numerator/Denominator⁠ = Quotient
	Algebraic Aspect Binary Continued Decimal Dyadic Egyptian Golden Silver Integer Irreducible Reduction Just intonation LCD Musical interval Paper size Percentage Unit