Теория динамо

Эта статья о предлагаемой теории источника магнитного поля планеты. Для объяснения работы механической динамо см. Динамо .

Иллюстрация механизма динамо, генерирующего магнитное поле Земли: конвекционные Земли токи жидкого металла во внешнем ядре , приводимые в движение тепловым потоком из внутреннего ядра, организованные в рулоны силой Кориолиса , генерируют циркулирующие электрические токи, которые поддерживают магнитное поле. .

В физике предлагает теория динамо механизм, с помощью которого небесное тело, такое как Земля или звезда, генерирует магнитное поле . Теория динамо описывает процесс, посредством которого вращающаяся, конвекционная и электропроводящая жидкость может поддерживать магнитное поле в астрономических масштабах времени. Считается, что динамо-машина является источником магнитного поля Земли , а также магнитных полей Меркурия и планет-гигантов .

История теории

Когда Уильям Гилберт опубликовал книгу «Магнете» в 1600 году, он пришел к выводу, что Земля обладает магнитными свойствами, и предложил первую гипотезу происхождения этого магнетизма: постоянный магнетизм, подобный тому, который обнаружен в магните . В 1822 году Андре-Мари Ампер предположил, что за земной магнетизм ответственны внутренние токи. . В 1919 году Джозеф Лармор предположил, что динамо-машина может генерировать поле. Однако даже после того, как он выдвинул свою гипотезу, некоторые видные учёные предложили альтернативные объяснения. Лауреат премии Нобелевской Патрик Блэкетт провел серию экспериментов в поисках фундаментальной связи между угловым моментом и магнитным моментом , но не нашел ее.

Уолтер М. Эльзассер , считающийся «отцом» ныне принятой теории динамо как объяснения магнетизма Земли, предположил, что это магнитное поле возникает в результате электрических токов, индуцированных в жидком внешнем ядре Земли. Он раскрыл историю магнитного поля Земли, впервые изучив магнитную ориентацию минералов в горных породах.

Чтобы сохранить магнитное поле от омического распада (который произойдет для дипольного поля через 20 000 лет), внешнее ядро ​​должно быть конвекционным. Конвекция , вероятно, представляет собой комбинацию тепловой и композиционной конвекции. Мантия контролирует скорость, с которой тепло извлекается из ядра. Источники тепла включают гравитационную энергию, выделяемую при сжатии ядра, гравитационную энергию, выделяемую при отторжении легких элементов (вероятно, серы , кислорода или кремния ) на внутренней границе ядра по мере его роста, скрытую теплоту кристаллизации на внутренней границе ядра, и радиоактивность калия , урана и тория .

На заре XXI века численное моделирование магнитного поля Земли не было успешно продемонстрировано. Первоначальные модели ориентированы на генерацию поля за счет конвекции во внешнем жидком ядре планеты. Генерацию сильного поля, подобного земному, можно было продемонстрировать, когда модель предполагала однородную температуру поверхности ядра и исключительно высокую вязкость основной жидкости. Расчеты, включавшие более реалистичные значения параметров, дали магнитные поля, менее похожие на земные, но показали, что уточнения модели в конечном итоге может привести к созданию точной аналитической модели. Небольшие изменения температуры поверхности ядра в пределах нескольких милликельвинов приводят к значительному увеличению конвективного потока и созданию более реалистичных магнитных полей.

Формальное определение

Теория динамо описывает процесс, посредством которого вращающаяся, конвекционная и электропроводящая жидкость поддерживает магнитное поле. Эта теория используется для объяснения наличия аномально долгоживущих магнитных полей в астрофизических телах. Проводящей жидкостью в геодинамо является жидкое железо во внешнем ядре, а в солнечном динамо — ионизированный газ в тахоклине . Динамо-теория астрофизических тел использует уравнения магнитогидродинамики для исследования того, как жидкость может непрерывно восстанавливать магнитное поле.

Когда-то считалось, что диполь , составляющий большую часть магнитного поля Земли и смещенный вдоль оси вращения на 11,3 градуса, был вызван постоянным намагничиванием материалов в Земле. Это означает, что теория динамо изначально использовалась для объяснения магнитного поля Солнца в его взаимосвязи с магнитным полем Земли. Однако эта гипотеза, первоначально предложенная Джозефом Лармором в 1919 году, была изменена благодаря обширным исследованиям вековых вариаций магнитного поля , палеомагнетизма (включая изменение полярности ), сейсмологии и обилия элементов в Солнечной системе. Также применение теорий Карла Фридриха Гаусса к магнитным наблюдениям показало, что магнитное поле Земли имеет внутреннее, а не внешнее происхождение.

Для работы динамо-машины необходимы три условия:

• Электропроводящая жидкая среда
• Кинетическая энергия, обеспечиваемая вращением планет.
• Внутренний источник энергии, обеспечивающий конвективные движения внутри жидкости.

В случае Земли магнитное поле создается и постоянно поддерживается за счет конвекции жидкого железа во внешнем ядре. Требованием для индукции поля является вращающаяся жидкость. Вращение во внешнем ядре обеспечивается эффектом Кориолиса, вызванным вращением Земли. Сила Кориолиса имеет тенденцию организовывать движения жидкости и электрические токи в столбцы (см. также столбцы Тейлора ), выровненные по оси вращения. Индукция или генерация магнитного поля описывается уравнением индукции : $${\frac {\partial \mathbf {B} }{\partial t}}=\eta \nabla ^{2}\mathbf {B} +\nabla \times (\mathbf {u} \times \mathbf {B} )$$где u — скорость, B — магнитное поле, t — время, а $\eta =1/(\sigma \mu )$ - магнитная диффузия с $\sigma$ электропроводность и $\mu$ проницаемость . Отношение второго члена в правой части к первому члену дает магнитное число Рейнольдса , безразмерное отношение адвекции магнитного поля к диффузии.

Приливный нагрев, поддерживающий динамо-машину

Приливные силы между небесными телами, вращающимися по орбите, вызывают трение, которое нагревает их недра. Это известно как приливной нагрев, и он помогает поддерживать внутреннюю часть в жидком состоянии. Для создания динамо-машины необходима жидкая внутренняя часть, способная проводить электричество. Энцелад Сатурна и Ио Юпитера имеют достаточно приливного нагрева, чтобы сжижать свои внутренние ядра, но они не могут создать динамо-машину, поскольку не могут проводить электричество. Меркурий, несмотря на свой небольшой размер, обладает магнитным полем, поскольку у него есть проводящее жидкое ядро, созданное за счет состава железа и трения, возникающего из-за его сильно эллиптической орбиты. На основании данных, полученных от намагниченных лунных пород, предполагается, что у Луны когда-то было магнитное поле, из-за ее кратковременного более близкого расстояния к Земле, вызывающего приливный нагрев. Орбита и вращение планеты помогают обеспечить жидкое ядро ​​и дополняют кинетическую энергию, поддерживающую действие динамо-машины.

Кинематическая теория динамо

В кинематической теории динамо поле скорости задано , а не является динамической переменной: модель не учитывает искажение потока под действием магнитного поля. Этот метод не может обеспечить изменяющееся во времени поведение полностью нелинейного хаотического динамо, но может быть использован для изучения того, как напряженность магнитного поля меняется в зависимости от структуры и скорости потока.

Используя уравнения Максвелла одновременно с ротором закона Ома , можно вывести то, что по сути является линейным уравнением собственных значений для магнитных полей ( B ), что можно сделать, если предположить, что магнитное поле независимо от поля скорости. Приходится к критическому магнитному числу Рейнольдса , выше которого сила потока достаточна для усиления наложенного магнитного поля, а ниже которого магнитное поле рассеивается.

Практическая мера возможных динамо-машин

Наиболее функциональной особенностью кинематической теории динамо является то, что ее можно использовать для проверки того, способно ли поле скоростей к действию динамо. Экспериментально прикладывая определенное поле скорости к небольшому магнитному полю, можно наблюдать, имеет ли магнитное поле тенденцию к росту (или нет) в ответ на приложенный поток. Если магнитное поле действительно растет, то система либо способна к динамо-действию, либо является динамо-машиной, а если магнитное поле не растет, то ее называют просто «не динамо».

Аналогичный метод, называемый мембранной парадигмой, представляет собой способ рассмотрения черных дыр , который позволяет выразить материал вблизи их поверхности на языке теории динамо.

Спонтанное нарушение топологической суперсимметрии.

Кинематическое динамо можно также рассматривать как явление самопроизвольного нарушения топологической суперсимметрии связанного с ним стохастического дифференциального уравнения, связанного с потоком фонового вещества. В рамках стохастической суперсимметричной теории эта суперсимметрия является внутренним свойством всех стохастических дифференциальных уравнений . Ее интерпретация заключается в том, что фазовое пространство модели сохраняет непрерывность посредством непрерывных потоков времени. Когда непрерывность этого потока спонтанно нарушается, система находится в стохастическом состоянии детерминированного хаоса . Другими словами, кинематическое динамо возникает из-за хаотического течения в основной фоновой материи.

Теория нелинейного динамо

Кинематическое приближение становится недействительным, когда магнитное поле становится достаточно сильным, чтобы влиять на движение жидкости. В этом случае на поле скоростей начинает действовать сила Лоренца , и поэтому уравнение индукции больше не является линейным в магнитном поле. В большинстве случаев это приводит к гашению амплитуды динамо. Такие динамо-машины иногда также называют гидромагнитными динамо-машинами . Практически все динамо-машины в астрофизике и геофизике являются гидромагнитными динамо-машинами.

Основная идея теории состоит в том, что любое небольшое магнитное поле, существующее во внешнем ядре, создает в движущейся там жидкости токи за счет силы Лоренца. Эти токи создают дополнительное магнитное поле согласно закону Ампера . При движении жидкости токи переносятся таким образом, что магнитное поле становится сильнее (пока $\;\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )\;$ отрицательный ). Таким образом, «затравочное» магнитное поле может становиться все сильнее и сильнее, пока не достигнет некоторого значения, которое связано с существующими немагнитными силами.

Численные модели используются для моделирования полностью нелинейных динамо-машин. Используются следующие уравнения:

• Уравнение индукции, представленное выше.
• Уравнения Максвелла для пренебрежимо малого электрического поля: $${\begin{aligned}&\nabla \cdot \mathbf {B} =0\\[1ex]&\nabla \times \mathbf {B} =\mu _{0}\mathbf {J} \end{aligned}}$$
• Уравнение неразрывности сохранения массы , для которого приближение Буссинеска : часто используется $$\nabla \cdot \mathbf {u} =0,$$
• Уравнение Навье-Стокса сохранения импульса , опять же в том же приближении, с магнитной силой и силой гравитации в качестве внешних сил: $${\frac {D\mathbf {u} }{Dt}}=-{\frac {1}{\rho _{0}}}\nabla p+\nu \nabla ^{2}\mathbf {u} +\rho '\mathbf {g} +2{\boldsymbol {\Omega }}\times \mathbf {u} +{\boldsymbol {\Omega }}\times {\boldsymbol {\Omega }}\times \mathbf {R} +{\frac {1}{\rho _{0}}}\mathbf {J} \times \mathbf {B} ~,$$ где $\,\nu \,$ – кинематическая вязкость , $\,\rho _{0}\,$средняя плотность и $\rho '$ - возмущение относительной плотности, обеспечивающее плавучесть (для тепловой конвекции $\;\rho '=\alpha \Delta T\;$ где $\,\alpha \,$ – коэффициент теплового расширения ), $\,\Omega \,$ - скорость вращения Земли , а $\,\mathbf {J} \,$ – плотность электрического тока.
• Уравнение переноса, обычно тепла (иногда концентрации легких элементов): $${\frac {\,\partial T\,}{\partial t}}=\kappa \nabla ^{2}T+\varepsilon$$ где Т — температура, $\;\kappa =k/\rho c_{p}\;$ – коэффициент температуропроводности с k , коэффициентом теплопроводности $\,c_{p}\,$ теплоемкость, -и $\rho$ плотность и $\varepsilon$ является дополнительным источником тепла. Часто давление представляет собой динамическое давление без учета гидростатического давления и центростремительного потенциала.

Затем эти уравнения обезразмериваются с введением безразмерных параметров: $$R_{\mathsf {a}}={\frac {\,g\alpha TD^{3}\,}{\nu \kappa }}\;,\quad E={\frac {\nu }{\,\Omega D^{2}\,}}\;,\quad P_{\mathsf {r}}={\frac {\,\nu \,}{\kappa }}\;,\quad P_{\mathsf {m}}={\frac {\,\nu \,}{\eta }}$$где Ra _, — число Рэлея E — число Экмана , P _r и P _{m —} число Прандтля и магнитное число Прандтля . Масштабирование магнитного поля часто осуществляется в числа Эльзассера . единицах $B=(\rho \Omega /\sigma )^{1/2}.$

Преобразование энергии между магнитной и кинематической энергией

Скалярное произведение приведенной выше формы уравнения Навье-Стокса на $\;\rho _{0}\mathbf {u} \;$ дает скорость увеличения плотности кинетической энергии, $\;{\tfrac {1}{2}}\rho _{0}u^{2}c\;$, с левой стороны. Тогда последнее слагаемое в правой части равно $\;\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )\;$, локальный вклад в кинетическую энергию, обусловленный силой Лоренца .

Скалярное произведение уравнения индукции с ${\textstyle {\tfrac {1}{\mu _{0}}}\mathbf {B} }$ дает скорость увеличения плотности магнитной энергии, $\;{\tfrac {1}{2}}\mu _{0}B^{2}\;$, с левой стороны. Тогда последнее слагаемое в правой части равно ${\textstyle {\tfrac {1}{\mu _{0}}}\mathbf {B} \cdot \left(\nabla \times \left(\mathbf {u} \times \mathbf {B} \right)\right)\;.}$ Поскольку уравнение интегрировано по объему, этот член эквивалентен с точностью до граничного члена (и с двойным использованием тождества скалярного тройного произведения ) ${\textstyle \;-\mathbf {u} \cdot \left({\tfrac {1}{\mu _{0}}}\left(\nabla \times \mathbf {B} \right)\times \mathbf {B} \right)=-\mathbf {u} \cdot \left(\mathbf {J} \times \mathbf {B} \right)~}$ (где использовалось одно из уравнений Максвелла). Это локальный вклад в магнитную энергию, обусловленный движением жидкости.

Таким образом, термин $\;-\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )\;$ - скорость преобразования кинетической энергии в магнитную энергию. Оно должно быть неотрицательным, по крайней мере, в части объема, чтобы динамо-машина могла создавать магнитное поле.

Из диаграммы выше неясно, почему этот член должен быть положительным. Простой аргумент может быть основан на рассмотрении чистых эффектов. Чтобы создать магнитное поле, чистый электрический ток должен обернуться вокруг оси вращения планеты. В этом случае, чтобы член был положительным, чистый поток проводящего вещества должен быть направлен к оси вращения. На диаграмме показан только чистый поток от полюсов к экватору. Однако сохранение массы требует дополнительного потока от экватора к полюсам. Если бы этот поток шел вдоль оси вращения, это означает, что циркуляция будет завершаться потоком от показанных к оси вращения, производя желаемый эффект.

Порядок величины магнитного поля, создаваемого динамо-машиной Земли.

Приведенная выше формула для скорости преобразования кинетической энергии в магнитную энергию эквивалентна скорости работы, совершаемой силой $\;\mathbf {J} \times \mathbf {B} \;$ на внешнее ядро, скорость которого равна $\mathbf {u}$. Эта работа является результатом действия немагнитных сил на жидкость.

Из них гравитационная сила и центробежная сила консервативны и , следовательно, не вносят общего вклада в движение жидкости в замкнутых контурах. Число Экмана (определенное выше), которое представляет собой соотношение между двумя оставшимися силами, а именно вязкостью и силой Кориолиса, очень мало внутри внешнего ядра Земли, поскольку его вязкость мала (1,2–1,5 × 10 ⁻² паскаль-секунда ) из-за его ликвидности.

Таким образом, основной усредненный по времени вклад в работу вносит сила Кориолиса, величина которой равна $\;-2\rho \,\mathbf {\Omega } \times \mathbf {u} \;,$ хотя это количество и $\mathbf {J} \times \mathbf {B}$ связаны лишь косвенно и, как правило, не равны локально (таким образом, они влияют друг на друга, но не в одном и том же месте и времени).

Плотность тока J сама по себе является результатом действия магнитного поля согласно закону Ома . Опять же, из-за движения материи и течения тока это не обязательно поле в том же месте и в то же время. Однако эти соотношения все еще можно использовать для вывода порядков рассматриваемых величин.

По порядку величины, $\;J\,B\sim \rho \,\Omega \,u\;$ и $\;J\sim \sigma uB\;$, давая $\;\sigma \,u\,B^{2}\sim \rho \,\Omega \,u\;,$ или: $$B\sim {\sqrt {{\frac {\,\rho \,\Omega \,}{\sigma }}\;}}$$

Точное соотношение между обеими частями — это квадратный корень из числа Эльзассера .

Обратите внимание, что направление магнитного поля не может быть выведено из этого приближения (по крайней мере, его знак), поскольку оно выглядит квадратичным и даже иногда переворачивается , хотя в целом оно лежит на той же оси, что и ось магнитного поля. $\mathbf {\Omega }$.

Для внешнего ядра земли ρ составляет примерно 10 ⁴ кг/м ³ ,   Ом = 2 π /день = 7,3×10 ⁻⁵ /секунда, а σ составляет примерно 10 ⁷ Ой ⁻¹ м ⁻¹  . Это дает 2,7×10 ⁻⁴  Тесла .

Магнитное поле магнитного диполя имеет обратную кубическую зависимость от расстояния, поэтому его порядок величины на поверхности земли можно аппроксимировать, умножив приведенный выше результат на ( R _{внешнее ядро} ​​⁄ R _Земля ) ³ = ( 2890 ⁄ 6370 ) ³ = 0,093, что дает 2,5×10 ⁻⁵ Тесла, недалеко от измеренного значения 3х10 ⁻⁵ Тесла на экваторе .

Численные модели

Визуальное представление модели Глацмайера до инверсии диполя.

В целом модели геодинамо пытаются создать магнитные поля, соответствующие наблюдаемым данным, при определенных условиях и уравнениях, как упомянуто в разделах выше. Успешная реализация уравнений магнитогидродинамики имела особое значение, поскольку они привели модели динамо к самосогласованности. Хотя модели геодинамо особенно распространены, модели динамо не обязательно ограничиваются геодинамо; Интересны также солнечные и общие модели динамо. Изучение моделей динамо полезно в области геофизики, поскольку оно может определить, как различные механизмы формируют магнитные поля, подобные тем, которые производятся астрофизическими телами, такими как Земля, и как они заставляют магнитные поля проявлять определенные особенности, такие как переворот полюсов.

Уравнения, используемые в численных моделях динамо, очень сложны. На протяжении десятилетий теоретики были ограничены описанными выше двумерными кинематическими моделями динамо , в которых движение жидкости выбирается заранее и рассчитывается влияние на магнитное поле. Переход от линейных к нелинейным трехмерным моделям динамо в значительной степени сдерживался поиском решений уравнений магнитной гидродинамики, которые устраняют необходимость во многих предположениях, сделанных в кинематических моделях, и допускают самосогласованность.

Визуальное представление модели Глацмайера во время разворота диполя.

Первые самосогласованные модели динамо, определяющие как движение жидкости, так и магнитное поле, были разработаны двумя группами в 1995 году, одна в Японии. и один в США. Последний был создан как модель геодинамо и привлек к себе значительное внимание, поскольку успешно воспроизводил некоторые характеристики поля Земли. После этого прорыва произошел большой всплеск разработки разумных трехмерных моделей динамо.

Хотя в настоящее время существует множество самосогласованных моделей, между ними существуют существенные различия как по результатам, которые они дают, так и по способу их разработки. Учитывая сложность разработки модели геодинамо, существует много мест, где могут возникнуть расхождения, например, при принятии предположений, касающихся механизмов, обеспечивающих энергию динамо, при выборе значений параметров, используемых в уравнениях, или при нормализации уравнений. Несмотря на множество возможных различий, большинство моделей имеют общие характеристики, такие как четкие осевые диполи. Во многих из этих моделей такие явления, как вековые вариации и смена геомагнитной полярности . также были успешно воссозданы

Наблюдения

Визуальное представление модели Глацмайера после инверсии диполя.

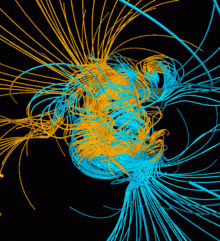
Многие наблюдения можно сделать на моделях динамо. Модели можно использовать для оценки того, как магнитные поля меняются со временем, и их можно сравнивать с наблюдаемыми палеомагнитными данными, чтобы найти сходство между моделью и Землей. Однако из-за неопределенности палеомагнитных наблюдений сравнения могут быть не совсем достоверными и полезными. Упрощенные модели геодинамо показали взаимосвязь между числом динамо (определяемым дисперсией скоростей вращения во внешнем ядре и зеркально-асимметричной конвекцией (например, когда конвекция благоприятствует одному направлению на севере и другому на юге)) и переполюсовкой магнитных полюсов. так же обнаружено сходство между геодинамо и солнечным динамо. Во многих моделях оказывается, что магнитные поля имеют несколько случайные величины, которые следуют нормальной тенденции и в среднем достигают нуля. В дополнение к этим наблюдениям можно сделать общие наблюдения о механизмах, приводящих в действие геодинамо, основываясь на том, насколько точно модель отражает фактические данные, собранные с Земли.

Современное моделирование

Сложность моделирования динамо настолько велика, что модели геодинамо ограничены нынешней мощностью суперкомпьютеров , в частности потому, что вычисление чисел Экмана и Рэлея внешнего ядра чрезвычайно сложно и требует огромного количества вычислений.

Многие улучшения были предложены в моделировании динамо после прорыва в области самосогласования в 1995 году. Одним из предложений по изучению сложных изменений магнитного поля является применение спектральных методов для упрощения вычислений. В конечном счете, пока не будут достигнуты значительные улучшения в мощности компьютеров, методы расчета реалистичных моделей динамо придется сделать более эффективными, поэтому улучшение методов расчета модели имеет большое значение для развития численного моделирования динамо.

Известные люди

• Станислав Иванович Брагинский , геофизик-исследователь

См. также

• Теорема об антидинамо
• Вращающееся магнитное поле
• Светская вариация

Ссылки

• Деморест, Пол (21 мая 2001 г.). «Теория динамо и магнитное поле Земли (курсовая работа)» (PDF) . Архивировано из оригинала (PDF) 21 февраля 2007 года . Проверено 14 октября 2011 г.
• Фитцпатрик, Ричард (18 мая 2002 г.). «Теория МГД-динамо» . Физика плазмы . Техасский университет в Остине . Проверено 14 октября 2011 г.
• Меррилл, Рональд Т.; МакЭлхинни, Майкл В.; Макфадден, Филипп Л. (1996). Магнитное поле Земли: палеомагнетизм, ядро ​​и глубокая мантия . Академическая пресса . ISBN  978-0-12-491246-5 .
• Стерн, Дэвид П. «Глава 12: Динамо-процесс» . Великий Магнит Земля . Проверено 14 октября 2011 г.
• Стерн, Дэвид П. «Глава 13: Динамо в ядре Земли» . Великий Магнит Земля . Проверено 14 октября 2011 г.