Алгоритм умножения

Алгоритм умножения — это алгоритм (или метод) умножения двух чисел. В зависимости от размера чисел разные алгоритмы более эффективны, чем другие. Известно множество алгоритмов, и по этой теме было проведено много исследований.

Самый старый и простой метод, известный с древности как длинное умножение или школьное умножение , состоит в умножении каждой цифры первого числа на каждую цифру второго и сложении результатов. Это имеет сложность временную $O(n^{2})$, где n — количество цифр. Если это делается вручную, это также можно перефразировать как умножение метода сетки или умножение решетки . В программном обеспечении это можно назвать «сдвиг и сложение», поскольку побитовый сдвиг и сложение — единственные необходимые две операции.

В 1960 году Анатолий Карацуба открыл умножение Карацубы , положив начало потоку исследований алгоритмов быстрого умножения. Этот метод использует три умножения, а не четыре для умножения двух двузначных чисел. (Вариант этого метода также можно использовать для умножения комплексных чисел быстрого .) При рекурсивном выполнении временная сложность равна $O(n^{\log _{2}3})$. Разделение чисел более чем на две части приводит к умножению Тума-Кука ; например, использование трех частей приводит к алгоритму Тоом-3 . Использование многих частей может привести к тому, что показатель степени будет сколь угодно близок к 1, но постоянный коэффициент также вырастет, что делает это непрактичным.

В 1968 году был открыт алгоритм Шёнхаге-Штрассена , который использует преобразование Фурье по модулю . Имеет временную сложность $O(n\log n\log \log n)$. В 2007 году Мартин Фюрер предложил алгоритм сложности $O(n\log n2^{\Theta (\log ^{*}n)})$. В 2014 году Харви, Йорис ван дер Хувен и Лесерф предложили сложную модель. $O(n\log n2^{3\log ^{*}n})$, что делает неявную константу явной; это было улучшено до $O(n\log n2^{2\log ^{*}n})$ в 2018 году. Наконец, в 2019 году Харви и ван дер Хувен придумали алгоритм со сложностью $O(n\log n)$. Это соответствует предположению Шенхаге и Штрассена о том, что это будет оптимальная граница, хотя сегодня это остается гипотезой .

Алгоритмы целочисленного умножения также можно использовать для умножения многочленов с помощью метода замены Кронекера .

Длинное умножение

Если используется позиционная система счисления , в школах преподают естественный способ умножения чисел. как длинное умножение , иногда называемое умножением начальной школы , иногда называемое стандартным алгоритмом : умножьте множимое на каждую цифру множителя , а затем сложите все правильно сдвинутые результаты. Требуется запоминание таблицы умножения однозначных цифр.

Это обычный алгоритм умножения больших чисел вручную по основанию 10. Человек, производящий долгое умножение на бумаге, записывает все произведения, а затем складывает их; пользователь счеты суммирует продукты, как только каждое из них будет вычислено.

Пример

В этом примере используется длинное умножение для умножения 23 958 233 (множимое) на 5 830 (множитель) и получается результат (произведение) 139 676 498 390.

      23958233
×         5830
———————————————
      00000000 ( =  23,958,233 ×     0)
     71874699  ( =  23,958,233 ×    30)
   191665864   ( =  23,958,233 ×   800)
+ 119791165    ( =  23,958,233 × 5,000)
———————————————
  139676498390 ( = 139,676,498,390)

Другие обозначения

В некоторых странах, таких как Германия , указанное выше умножение изображается аналогичным образом, но исходное произведение остается горизонтальным, а вычисления начинаются с первой цифры множителя:

23958233 · 5830
———————————————
   119791165
    191665864
      71874699
       00000000 
———————————————
   139676498390

Ниже псевдокод описывает процесс вышеуказанного умножения. Он сохраняет только одну строку для хранения суммы, которая в конечном итоге становится результатом. Обратите внимание, что оператор «+=» используется для обозначения суммы существующего значения и операции сохранения (аналогично таким языкам, как Java и C) для компактности.

multiply(a[1..p], b[1..q], base)                            // Operands containing rightmost digits at index 1
  product = [1..p+q]                                        // Allocate space for result
  for b_i = 1 to q                                          // for all digits in b
    carry = 0
    for a_i = 1 to p                                        // for all digits in a
      product[a_i + b_i - 1] += carry + a[a_i] * b[b_i]
      carry = product[a_i + b_i - 1] / base
      product[a_i + b_i - 1] = product[a_i + b_i - 1] mod base
    product[b_i + p] = carry                               // last digit comes from final carry
  return product

Использование в компьютерах

Некоторые микросхемы реализуют длинное умножение аппаратно или в микрокоде для различных размеров целых чисел и слов с плавающей запятой. В арифметике произвольной точности обычно используется длинное умножение с базовым набором 2. ^В , где w — количество бит в слове, для умножения относительно небольших чисел. Чтобы перемножить два числа с n цифрами этим методом, нужно около n ² операции. Более формально, умножение двух n- значных чисел с использованием длинного умножения требует Θ ( n ² ) однозначные операции (сложение и умножение).

При программной реализации длинные алгоритмы умножения должны иметь дело с переполнением во время сложения, что может быть дорогостоящим. Типичное решение — представить число по небольшой базе b , например, 8 b — представимое машинное целое число. Затем можно выполнить несколько добавлений, прежде чем произойдет переполнение. Когда число становится слишком большим, мы добавляем его часть к результату или переносим и отображаем оставшуюся часть обратно в число, меньшее b . Этот процесс называется нормализацией . Ричард Брент использовал этот подход в своем пакете MP для Фортрана.

Первоначально компьютеры использовали алгоритм, очень похожий на длинное умножение по основанию 2, но современные процессоры оптимизировали схему для быстрого умножения с использованием более эффективных алгоритмов ценой более сложной аппаратной реализации. В системе счисления два длинные умножения иногда называют «сдвигом и сложением» , поскольку алгоритм упрощается и состоит всего лишь из сдвига влево (умножения на степени двойки) и сложения. Большинство доступных в настоящее время микропроцессоров реализуют этот или другие подобные алгоритмы (например, кодирование Бута ) для различных целых чисел и размеров с плавающей запятой в аппаратных множителях или в микрокоде .

На доступных в настоящее время процессорах команда побитового сдвига обычно (но не всегда) быстрее, чем инструкция умножения, и может использоваться для умножения (сдвига влево) и деления (сдвига вправо) на степени двойки. Умножение на константу и деление на константу можно реализовать с помощью последовательности сдвигов и сложений или вычитаний. Например, есть несколько способов умножения на 10, используя только побитовый сдвиг и сложение.

 ((x << 2) + x) << 1 # Here 10*x is computed as (x*2^2 + x)*2
 (x << 3) + (x << 1) # Here 10*x is computed as x*2^3 + x*2

В некоторых случаях такие последовательности сдвигов, сложений и вычитаний превосходят по производительности аппаратные умножители и особенно делители. Деление на число вида $2^{n}$ или $2^{n}\pm 1$ часто можно преобразовать в такую ​​короткую последовательность.

Алгоритмы умножения вручную

Помимо стандартного длинного умножения, существует несколько других методов ручного умножения. Такие алгоритмы могут быть разработаны ради скорости, простоты вычислений или образовательной ценности, особенно когда компьютеры или таблицы умножения недоступны.

Сетчатый метод

Основная статья: Умножение метода сетки

Метод сетки (или метод коробки) — это вводный метод многозначного умножения, который часто преподается ученикам начальной или начальной школы . С конца 1990-х годов это стандартная часть национальной учебной программы по математике в начальной школе в Англии и Уэльсе.

Оба фактора разбиваются («разделяются») на части из сотен, десятков и единиц, а затем произведения этих частей явно вычисляются на относительно простом этапе, состоящем только из умножения, прежде чем эти вклады затем суммируются для получения окончательного ответа в виде отдельный этап добавления.

Например, расчет 34 × 13 можно выполнить с использованием сетки:

  300
   40
   90
 + 12
 ————
  442

×	30	4
10	300	40
3	90	12

с последующим сложением до получения 442 либо в одной сумме (см. справа), либо путем формирования построчных сумм (300 + 40) + (90 + 12) = 340 + 102 = 442.

Этот подход к расчетам (хотя и не обязательно с явным расположением сетки) также известен как алгоритм частичных произведений . Суть его заключается в вычислении простых умножений отдельно, а все сложение оставляют на завершающем этапе суммирования.

Метод сетки в принципе можно применять к факторам любого размера, хотя количество субпродуктов становится громоздким по мере увеличения количества цифр. Тем не менее, это рассматривается как полезный явный метод, позволяющий представить идею многозначного умножения; и в эпоху, когда большинство вычислений умножения выполняются с помощью калькулятора или электронных таблиц, на практике это может оказаться единственным алгоритмом умножения, который когда-либо понадобится некоторым ученикам.

Решётчатое умножение

Основная статья: Решечное умножение

Сначала настройте сетку, отметив ее строки и столбцы числами, которые необходимо умножить. Затем заполните поля с цифрами десятков в верхних треугольниках и цифрами единиц внизу.

Наконец, просуммируйте по диагональным участкам и перенесите по мере необходимости, чтобы получить ответ.

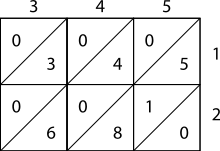
Решётчатое или решетчатое умножение алгоритмически эквивалентно длинному умножению. Для этого требуется подготовить решетку (сетку, нарисованную на бумаге), которая будет служить ориентиром для вычислений и отделять все умножения от сложений . В Европе он был представлен в 1202 году в Фибоначчи » «Liber Abaci . Фибоначчи описал эту операцию как мысленную, используя правую и левую руки для выполнения промежуточных вычислений. Матракчи Насух ​​представил 6 различных вариантов этого метода в книге XVI века «Умдет-уль-Хисаб». Он широко использовался в школах Эндеруна по всей Османской империи. Кости Непера или стержни Непьера также использовали этот метод, как было опубликовано Нейпиром в 1617 году, в год его смерти.

Как показано в примере, множимое и множитель записываются выше и справа от решетки или сита. Он встречается в «Арифметике» Мухаммада ибн Мусы аль-Хорезми , одном из источников Леонардо, упомянутом Сиглером, автором «Liber Abaci Фибоначчи», 2002.

• На этапе умножения решетка заполняется двузначными произведениями соответствующих цифр, обозначающих каждую строку и столбец: цифра десятков помещается в верхний левый угол.
• На этапе сложения решетка суммируется по диагоналям.
• Наконец, если необходима фаза переноса, ответ, показанный вдоль левой и нижней сторон решетки, преобразуется в нормальную форму путем переноса десятичных цифр, как при длинном сложении или умножении.

Пример

На рисунках справа показано, как вычислить 345 × 12 с помощью решеточного умножения. В качестве более сложного примера рассмотрим рисунок ниже, на котором показано вычисление 23 958 233, умноженного на 5 830 (множитель); результат — 139 676 498 390. Обратите внимание, что 23 958 233 находится в верхней части решетки, а 5 830 — в правой части. Продукты заполняют решетку, а сумма этих продуктов (по диагонали) находится вдоль левой и нижней сторон. Затем эти суммы суммируются, как показано.

2 3 9 5 8 2 3 3 +---+---+---+---+---+---+---+---+- |1 /|1 /|4 /|2 /|4 /|1 /|1 /|1 /| | / | / | / | / | / | / | / | / | 5 01|/ 0|/ 5|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5| +---+---+---+---+---+---+---+---+- |1 /|2 /|7 /|4 /|6 /|1 /|2 /|2 /| | / | / | / | / | / | / | / | / | 8 02|/ 6|/ 4|/ 2|/ 0|/ 4|/ 6|/ 4|/ 4| +---+---+---+---+---+---+---+---+- |0 /|0 /|2 /|1 /|2 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 3 17|/ 6|/ 9|/ 7|/ 5|/ 4|/ 6|/ 9|/ 9| +---+---+---+---+---+---+---+---+- |0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 0 24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0| +---+---+---+---+---+---+---+---+- 26 15 13 18 17 13 09 00

01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390

= 139,676,498,390

Русское крестьянское умножение

Основная статья: Крестьянское умножение

Бинарный метод также известен как крестьянское умножение, поскольку он широко использовался людьми, которые относятся к крестьянам и поэтому не запомнили таблицы умножения, необходимые для длительного умножения. Алгоритм использовался в Древнем Египте. Его основные преимущества заключаются в том, что ему можно быстро научиться, он не требует запоминания и может выполняться с использованием жетонов, таких как покерные фишки , если бумага и карандаш недоступны. Недостатком является то, что оно требует больше шагов, чем длинное умножение, поэтому для больших чисел оно может оказаться громоздким.

Описание

На бумаге запишите в один столбец числа, которые вы получите, если неоднократно уменьшать множитель вдвое, игнорируя остаток; в столбце рядом с ним многократно удваивайте множимое. Вычеркните каждую строку, в которой последняя цифра первого числа четная, и сложите оставшиеся числа во втором столбце, чтобы получить произведение.

Примеры

В этом примере крестьянское умножение используется для умножения 11 на 3 и получения результата 33.

Decimal:     Binary:
11   3       1011  11
5    6       101  110
2   12       10  1100
1   24       1  11000
    ——         ——————
    33         100001

Подробное описание шагов:

• 11 и 3 написаны вверху.
• 11 уменьшается вдвое (5,5), а 3 удваивается (6). Дробная часть отбрасывается (5,5 становится 5).
• 5 уменьшается вдвое (2,5), а 6 удваивается (12). Дробная часть отбрасывается (2,5 становится 2). Цифра в левом столбце (2) четная , поэтому цифра в правом столбце (12) отбрасывается.
• 2 делится пополам (1), а 12 удваивается (24).
• Все невычеркнутые значения суммируются: 3+6+24=33.

Этот метод работает, поскольку умножение является распределительным , поэтому:

${\begin{aligned}3\times 11&=3\times (1\times 2^{0}+1\times 2^{1}+0\times 2^{2}+1\times 2^{3})\\&=3\times (1+2+8)\\&=3+6+24\\&=33.\end{aligned}}$

Более сложный пример с использованием цифр из предыдущих примеров (23 958 233 и 5 830):

Decimal:             Binary:
5830  23958233       1011011000110  1011011011001001011011001
2915  47916466       101101100011  10110110110010010110110010
1457  95832932       10110110001  101101101100100101101100100
728  191665864       1011011000  1011011011001001011011001000
364  383331728       101101100  10110110110010010110110010000
182  766663456       10110110  101101101100100101101100100000
91  1533326912       1011011  1011011011001001011011001000000
45  3066653824       101101  10110110110010010110110010000000
22  6133307648       10110  101101101100100101101100100000000
11 12266615296       1011  1011011011001001011011001000000000
5  24533230592       101  10110110110010010110110010000000000
2  49066461184       10  101101101100100101101100100000000000
1  98132922368       1  1011011011001001011011001000000000000
  ————————————          1022143253354344244353353243222210110 (before carry)
  139676498390         10000010000101010111100011100111010110

Умножение четверти квадрата

В некоторых случаях можно использовать эту формулу, чтобы облегчить выполнение задач умножения:

${\frac {\left(x+y\right)^{2}}{4}}-{\frac {\left(x-y\right)^{2}}{4}}={\frac {1}{4}}\left(\left(x^{2}+2xy+y^{2}\right)-\left(x^{2}-2xy+y^{2}\right)\right)={\frac {1}{4}}\left(4xy\right)=xy.$

В случае, когда $x$ и $y$ являются целыми числами, у нас есть это

$(x+y)^{2}\equiv (x-y)^{2}{\bmod {4}}$

потому что $x+y$ и $x-y$ либо оба четные, либо оба нечетные. Это означает, что

${\begin{aligned}xy&={\frac {1}{4}}(x+y)^{2}-{\frac {1}{4}}(x-y)^{2}\\&=\left((x+y)^{2}{\text{ div }}4\right)-\left((x-y)^{2}{\text{ div }}4\right)\end{aligned}}$

и достаточно (предварительно) вычислить целую часть квадратов, разделенную на 4, как в следующем примере.

Примеры

Ниже приведена таблица поиска четвертей квадратов, в которой остаток отброшен для цифр от 0 до 18; это позволяет умножать числа до 9×9 .

н	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
⌊ n 2 /4⌋	0	0	1	2	4	6	9	12	16	20	25	30	36	42	49	56	64	72	81

Если, например, вы захотели умножить 9 на 3, вы заметили, что сумма и разность равны 12 и 6 соответственно. Просмотр обоих этих значений в таблице дает 36 и 9, разница которых равна 27, что является произведением 9 и 3.

История умножения четверти квадрата

В доисторические времена умножение на четверть квадрата включало функцию пола ; что некоторые источники отнести к вавилонской математике (2000–1600 гг. до н. э.).

Антуан Вуазен опубликовал таблицу четвертей квадратов от 1 до 1000 в 1817 году в качестве вспомогательного средства при умножении. Более крупная таблица четвертей квадратов от 1 до 100 000 была опубликована Сэмюэлем Лаунди в 1856 году. и таблица от 1 до 200 000 Йозефа Блатера в 1888 году.

Четвертьквадратные умножители использовались в аналоговых компьютерах для формирования аналогового сигнала , который был продуктом двух аналоговых входных сигналов. В этом приложении сумма и разность двух входных напряжений формируются с помощью операционных усилителей . Квадрат каждого из них аппроксимируется с помощью кусочно-линейных схем. Наконец, разница двух квадратов формируется и масштабируется в одну четверть с использованием еще одного операционного усилителя.

В 1980 году Эверетт Л. Джонсон предложил использовать метод четверти квадрата в цифровом умножителе. Например, чтобы получить произведение двух 8-битных целых чисел, цифровое устройство формирует сумму и разность, ищет обе величины в таблице квадратов, берет разницу результатов и делит на четыре, сдвигая два бита в сторону числа. верно. Для 8-битных целых чисел таблица четвертей квадратов будет иметь 2 ⁹ −1=511 записей (одна запись для всего диапазона возможных сумм от 0 до 510, для разностей используются только первые 256 записей в диапазоне от 0 до 255) или 2 ⁹ −1 = 511 записей (для отрицательных разностей используется техника 2-дополнительных дополнений и 9-битной маскировки, которая позволяет избежать проверки знака различий), каждая запись имеет ширину 16 бит (значения записи взяты из (0²/4) = От 0 до (510²/4)=65025).

Метод четвертьквадратного умножителя принес пользу 8-битным системам, которые не поддерживают аппаратный умножитель. Чарльз Путни реализовал это для 6502 .

Вычислительная сложность умножения

Нерешенная задача в информатике :

Какой самый быстрый алгоритм умножения двух $n$-значные числа?

(еще нерешенные проблемы по информатике)

Направление исследований в области теоретической информатики касается количества однобитовых арифметических операций, необходимых для умножения двух $n$-битовые целые числа. Это известно как вычислительная сложность умножения. Обычные алгоритмы, выполненные вручную, имеют асимптотическую сложность $O(n^{2})$, но в 1960 году Анатолий Карацуба обнаружил, что возможна более высокая сложность (с помощью алгоритма Карацубы ).

В настоящее время алгоритмом с наилучшей вычислительной сложностью является алгоритм Дэвида Харви и Йориса ван дер Хувена 2019 года , который использует стратегии использования теоретико-числовых преобразований, представленных в алгоритме Шенхаге – Штрассена, для умножения целых чисел, используя только $O(n\log n)$ операции. Предполагается, что это наилучший алгоритм, но нижние границы $\Omega (n\log n)$ не известны.

Умножение Карацубы

Основная статья: Алгоритм Карацубы

Умножение Карацубы — это O( n ^{войти ₂ 3} ) ≈ O( n ^1.585 ) алгоритм «разделяй и властвуй», который использует рекурсию для объединения подвычислений.

Переписывая формулу, можно выполнять дополнительные вычисления/рекурсию. Выполняя рекурсию, можно решить эту проблему быстро.

Позволять $x$ и $y$ быть представлен как $n$-цифровые строки в некоторой базе $B$. Для любого положительного целого числа $m$ меньше, чем $n$, можно записать два заданных числа как

$x=x_{1}B^{m}+x_{0},$

$y=y_{1}B^{m}+y_{0},$

где $x_{0}$ и $y_{0}$ меньше, чем $B^{m}$. Затем продукт

${\begin{aligned}xy&=(x_{1}B^{m}+x_{0})(y_{1}B^{m}+y_{0})\\&=x_{1}y_{1}B^{2m}+(x_{1}y_{0}+x_{0}y_{1})B^{m}+x_{0}y_{0}\\&=z_{2}B^{2m}+z_{1}B^{m}+z_{0},\\\end{aligned}}$

где

$z_{2}=x_{1}y_{1},$

$z_{1}=x_{1}y_{0}+x_{0}y_{1},$

$z_{0}=x_{0}y_{0}.$

Эти формулы требуют четырех умножений и были известны Чарльзу Бэббиджу . Карацуба заметил, что $xy$ можно вычислить всего за три умножения ценой нескольких дополнительных сложений. С $z_{0}$ и $z_{2}$ как и прежде, можно заметить, что

${\begin{aligned}z_{1}&=x_{1}y_{0}+x_{0}y_{1}\\&=x_{1}y_{0}+x_{0}y_{1}+x_{1}y_{1}-x_{1}y_{1}+x_{0}y_{0}-x_{0}y_{0}\\&=x_{1}y_{0}+x_{0}y_{0}+x_{0}y_{1}+x_{1}y_{1}-x_{1}y_{1}-x_{0}y_{0}\\&=(x_{1}+x_{0})y_{0}+(x_{0}+x_{1})y_{1}-x_{1}y_{1}-x_{0}y_{0}\\&=(x_{1}+x_{0})(y_{0}+y_{1})-x_{1}y_{1}-x_{0}y_{0}\\&=(x_{1}+x_{0})(y_{1}+y_{0})-z_{2}-z_{0}.\\\end{aligned}}$

Из-за накладных расходов на рекурсию умножение Карацубы происходит медленнее, чем длинное умножение для малых значений n ; поэтому типичные реализации переключаются на длинное умножение для малых значений n .

Общий случай с умножением N чисел

Изучая закономерности после расширения, можно увидеть следующее:

$(x_{1}B^{m}+x_{0})(y_{1}B^{m}+y_{0})(z_{1}B^{m}+z_{0})(a_{1}B^{m}+a_{0})=$
$a_{1}x_{1}y_{1}z_{1}B^{4m}+a_{1}x_{1}y_{1}z_{0}B^{3m}+a_{1}x_{1}y_{0}z_{1}B^{3m}+a_{1}x_{0}y_{1}z_{1}B^{3m}$
$+a_{0}x_{1}y_{1}z_{1}B^{3m}+a_{1}x_{1}y_{0}z_{0}B^{2m}+a_{1}x_{0}y_{1}z_{0}B^{2m}+a_{0}x_{1}y_{1}z_{0}B^{2m}$
$+a_{1}x_{0}y_{0}z_{1}B^{2m}+a_{0}x_{1}y_{0}z_{1}B^{2m}+a_{0}x_{0}y_{1}z_{1}B^{2m}+a_{1}x_{0}y_{0}z_{0}B^{m}$
$+a_{0}x_{1}y_{0}z_{0}B^{m}+a_{0}x_{0}y_{1}z_{0}B^{m}+a_{0}x_{0}y_{0}z_{1}B^{m}+a_{0}x_{0}y_{0}z_{0}$

Каждому слагаемому соответствует уникальное двоичное число от 0 до $2^{N+1}-1$, например $a_{1}x_{1}y_{1}z_{1}\longleftrightarrow 1111,\ a_{1}x_{0}y_{1}z_{0}\longleftrightarrow 1010$ и т. д. Кроме того; B приводится к числу 1 в этой двоичной строке, умноженному на m.

Если выразить это в меньшем количестве терминов, мы получим:

$\prod _{j=1}^{N}(x_{j,1}B^{m}+x_{j,0})=\sum _{i=1}^{2^{N+1}-1}\prod _{j=1}^{N}x_{j,c(i,j)}B^{m\sum _{j=1}^{N}c(i,j)}=\sum _{j=0}^{N}z_{j}B^{jm}$, где $c(i,j)$ означает цифру номера i в позиции j. Обратите внимание, что $c(i,j)\in \{0,1\}$

$z_{0}=\prod _{j=1}^{N}x_{j,0}$
$z_{N}=\prod _{j=1}^{N}x_{j,1}$
$z_{N-1}=\prod _{j=1}^{N}(x_{j,0}+x_{j,1})-\sum _{i\neq N-1}^{N}z_{i}$

История

Алгоритм Карацубы был первым известным алгоритмом умножения, который асимптотически быстрее, чем длинное умножение. и, таким образом, его можно рассматривать как отправную точку теории быстрых умножений.

Тум-Кук

Основная статья: Умножение Тума – Кука

Другой метод умножения называется Тум-Кук или Тум-3. Метод Тума-Кука разбивает каждое число, подлежащее умножению, на несколько частей. Метод Тума-Кука является одним из обобщений метода Карацубы. Трехходовой алгоритм Тума-Кука может выполнить умножение размера 3N за стоимость пяти размера N. умножений Это ускоряет операцию в 9/5 раз, тогда как метод Карацубы ускоряет ее в 4/3.

Хотя использование все большего и большего количества частей может еще больше сократить время, затрачиваемое на рекурсивное умножение, накладные расходы на сложение и управление цифрами также растут. По этой причине метод преобразований Фурье обычно быстрее для чисел с несколькими тысячами цифр и асимптотически быстрее для еще больших чисел.

Улицы Шенхаге

Основная статья: алгоритм Шенхаге – Штрассена

Демонстрация умножения 1234 × 5678 = 7006652 с использованием быстрого преобразования Фурье (БПФ). теоретико-числовые преобразования Используются целых чисел по модулю 337, выбирая 85 как корень восьмой степени из единицы. Вместо основания 2 используется основание 10. ^В для иллюстративных целей.

Любое число по основанию B можно записать в виде многочлена:

$X=\sum _{i=0}^{N}{x_{i}B^{i}}$

Более того, умножение двух чисел можно рассматривать как произведение двух многочленов:

$XY=(\sum _{i=0}^{N}{x_{i}B^{i}})(\sum _{j=0}^{N}{y_{i}B^{j}})$

Потому что для $B^{k}$: $c_{k}=\sum _{(i,j):i+j=k}{a_{i}b_{j}}=\sum _{i=0}^{k}{a_{i}b_{k-i}}$, у нас есть свертка.

Используя БПФ (быстрое преобразование Фурье) с правилом свертки, мы можем получить

${\hat {f}}(a*b)={\hat {f}}(\sum _{i=0}^{k}{a_{i}b_{k-i}})={\hat {f}}(a)$ ● ${\hat {f}}(b)$. То есть; $C_{k}=a_{k}$ ● $b_{k}$, где $C_{k}$ – соответствующий коэффициент в пространстве Фурье. Это также можно записать как: fft(a * b) = fft(a) ● fft(b).

Мы имеем тот же коэффициент из-за линейности при преобразовании Фурье, а также потому, что эти полиномы состоят только из одного уникального термина на коэффициент:

${\hat {f}}(x^{n})=\left({\frac {i}{2\pi }}\right)^{n}\delta ^{(n)}$ и ${\hat {f}}(a\,X(\xi )+b\,Y(\xi ))=a\,{\hat {X}}(\xi )+b\,{\hat {Y}}(\xi )$

Правило свертки: ${\hat {f}}(X*Y)=\ {\hat {f}}(X)$ ● ${\hat {f}}(Y)$

Мы уменьшили нашу проблему свертки к проблеме продукта, через FFT.

Находя ifft (полиномиальную интерполяцию) для каждого $c_{k}$, получаем искомые коэффициенты.

Алгоритм использует стратегию «разделяй и властвуй», чтобы разделить проблему на подзадачи.

Его временная сложность составляет O( n log( n ) log(log( n ))).

История

Алгоритм был изобретен Штрассеном (1968). Это было сделано на практике, а теоретические гарантии были предоставлены в 1971 году Шенхаге и Штрассеном, что привело к созданию алгоритма Шёнхаге-Штрассена .

Дальнейшие улучшения

В 2007 году асимптотическая сложность умножения целых чисел была улучшена швейцарским математиком Мартином Фюрером из Университета штата Пенсильвания до n log( n ) 2. ^{Θ( логарифм * ( н ))} использование преобразований Фурье над комплексными числами , где журнал ^* обозначает повторный логарифм . Аниндья Де, Чандан Саха, Пиюш Курур и Рампрасад Саптариши предложили аналогичный алгоритм с использованием модульной арифметики в 2008 году, достигнув того же времени работы. В контексте приведенного выше материала последние авторы обнаружили, что N намного меньше 2. ^{3 тыс.} + 1, так что Z / NZ имеет корень (2 m )-й степени из единицы. Это ускоряет вычисления и снижает временную сложность. Однако эти последние алгоритмы быстрее, чем Шенхаге – Штрассен, только для непрактично больших входных данных.

В 2014 году Харви, Йорис ван дер Хувен и Лесерф дал новый алгоритм, который обеспечивает время работы $O(n\log n\cdot 2^{3\log ^{*}n})$, делая явным подразумеваемую константу в $O(\log ^{*}n)$ показатель. Они также предложили вариант своего алгоритма, который обеспечивает $O(n\log n\cdot 2^{2\log ^{*}n})$ но чья достоверность основана на стандартных гипотезах о распределении простых чисел Мерсенна . В 2016 году Кованов и Томе предложили алгоритм целочисленного умножения, основанный на обобщении простых чисел Ферма , который предположительно достигает границы сложности $O(n\log n\cdot 2^{2\log ^{*}n})$. Это соответствует условному результату Харви, ван дер Хувена и Лесерфа 2015 года, но использует другой алгоритм и основывается на другой гипотезе. В 2018 году Харви и ван дер Хувен использовали подход, основанный на существовании коротких векторов решетки, гарантированных теоремой Минковского, для доказательства безусловной границы сложности $O(n\log n\cdot 2^{2\log ^{*}n})$.

В марте 2019 года Дэвид Харви и Йорис ван дер Хувен объявили об открытии алгоритма умножения O ( n log n ) . Он был опубликован в Annals of Mathematics в 2021 году. Поскольку Шёнхаге и Штрассен предсказали, что n log( n ) является «наилучшим возможным» результатом, Харви сказал: «…   ожидается, что наша работа станет концом пути к решению этой проблемы, хотя мы пока не знаем, как ее решить». докажите это строго».

Нижние границы

Существует тривиальная нижняя оценка Ω ( n ) для умножения двух n -битных чисел на одном процессоре; не известен ни алгоритм сопоставления (на обычных машинах, то есть на машинах, эквивалентных Тьюрингу), ни какая-либо более точная нижняя граница. Умножение лежит вне AC ⁰ [ p ] для любого простого p , что означает, что не существует семейства схем полиномиального (или даже субэкспоненциального) размера постоянной глубины, использующих вентили AND, OR, NOT и MOD _p, которые могут вычислить произведение. Это следует из приведения MOD _q к умножению с постоянной глубиной. Нижние оценки умножения известны также для некоторых классов ветвящихся программ .

Умножение комплексных чисел

Комплексное умножение обычно включает четыре умножения и два сложения.

$(a+bi)(c+di)=(ac-bd)+(bc+ad)i.$

Или

${\begin{array}{c|c|c}\times &a&bi\\\hline c&ac&bci\\\hline di&adi&-bd\end{array}}$

Как заметил Питер Унгар в 1963 году, можно уменьшить количество умножений до трех, используя по существу те же вычисления, что и алгоритм Карацубы . Произведение ( a + bi ) · ( c + di ) можно вычислить следующим образом.

k ₁ знак равно c · ( а + б )

k ₂ знак равно а · ( d - c )

k ₃ знак равно б · ( c + d )

Действительная часть = k ₁ − k ₃

Мнимая часть знак равно k ₁ + k ₂ .

Этот алгоритм использует только три умножения вместо четырех и пять сложений или вычитаний вместо двух. Если умножение обходится дороже, чем три сложения или вычитания, как при ручном расчете, то есть выигрыш в скорости. На современных компьютерах умножение и сложение могут занять примерно одно и то же время, поэтому прироста скорости может не быть. Существует компромисс в том, что при использовании плавающей запятой может быть некоторая потеря точности.

Для быстрых преобразований Фурье (БПФ) (или любого линейного преобразования ) комплексные умножения производятся на постоянные коэффициенты c + di (называемые коэффициентами поворота в БПФ), и в этом случае два сложения ( d − c и c + d ) могут быть вычислены заранее. . Следовательно, требуются только три умножения и три сложения. Однако такой способ замены умножения на сложение может оказаться бесполезным для современных модулей с плавающей запятой .

Полиномиальное умножение

Все приведенные выше алгоритмы умножения также можно расширить для умножения многочленов . В качестве альтернативы можно использовать технику замены Кронекера для преобразования задачи умножения многочленов в одно двоичное умножение.

Методы длинного умножения можно обобщить, чтобы можно было умножать алгебраические формулы:

 14ac - 3ab + 2 multiplied by ac - ab + 1

 14ac  -3ab   2
   ac   -ab   1
 ————————————————————
 14a2c2  -3a2bc   2ac
        -14a2bc         3 a2b2  -2ab
                 14ac           -3ab   2
 ———————————————————————————————————————
 14a2c2 -17a2bc   16ac  3a2b2    -5ab  +2
 =======================================

В качестве еще одного примера умножения на основе столбцов рассмотрим умножение 23 длинных тонн (т), 12 центнеров (центнеров) и 2 четвертей (кварта) на 47. В этом примере используются меры эвердюпуа : 1 т = 20 центнеров, 1 центнер = 4 квартеры.

    t    cwt  qtr
   23     12    2
               47 x
 ————————————————
  141     94   94
  940    470
   29     23
 ————————————————
 1110    587   94
 ————————————————
 1110      7    2
 =================  Answer: 1110 ton 7 cwt 2 qtr

Сначала умножаем четверти на 47, результат 94 записывается в первую рабочую область. Затем умножьте cwt 12*47 = (2 + 10)*47, но пока не складывайте частичные результаты (94, 470). Аналогичным образом умножьте 23 на 47, получив (141, 940). В столбце четвертей суммируется результат, и результат помещается во вторую рабочую область (в данном случае это тривиальный ход). 94 четверти — это 23 центнера и 2 четверти, поэтому поставьте 2 в ответ, а 23 — в следующий столбец слева. Теперь сложите три записи в столбце cwt и получите 587. Это 29 t 7 cwt, поэтому впишите 7 в ответ и 29 в столбец слева. Теперь сложите столбец тонн. Никакой настройки не требуется, поэтому результат просто копируется.

Та же схема и методы могут использоваться для любых традиционных единиц измерения и недесятичных валют, таких как старая британская система £SD .

См. также

• Двоичный множитель
• Множитель Дадда
• Алгоритм деления
• Схема Хорнера для оценки полинома
• Логарифм
• Ментальный расчет
• Теоретико-числовое преобразование
• Простафаэрез
• Логарифмическая линейка
• Система Трахтенберга
• Система счисления с остатком § Умножение для другого быстрого алгоритма умножения, особенно эффективного, когда многие операции выполняются последовательно, например, в линейной алгебре.
• Дерево Уоллеса

Дальнейшее чтение

• Уоррен младший, Генри С. (2013). Хакерское наслаждение (2-е изд.). Аддисон Уэсли - Pearson Education, Inc. ISBN  978-0-321-84268-8 .
• Савард, Джон Дж. Г. (2018) [2006]. «Продвинутые арифметические методы» . четырехблок . Архивировано из оригинала 3 июля 2018 г. Проверено 16 июля 2018 г.
• Йоханссон, Кенни (2008). Вычисления на основе сдвига и сложения малой мощности и низкой сложности (PDF) (Диссертация). Линчёпингские исследования в области науки и технологий (1-е изд.). Линчёпинг, Швеция: Факультет электротехники, Университет Линчёпинга . ISBN  978-91-7393-836-5 . ISSN   0345-7524 . № 1201. Архивировано (PDF) из оригинала 13 августа 2017 г. Проверено 23 августа 2021 г. (x+268 страниц)

Внешние ссылки

Основная арифметика

• Множество способов арифметики в повседневной математике UCSMP
• Презентация Powerpoint о древней математике.
• Флеш-видео о решеточном умножении

Расширенные алгоритмы

• Алгоритмы умножения, используемые GMP