Число Ферма
| Назван в честь | Пьер де Ферма |
|---|---|
| Количество известных терминов | 5 |
| Предполагаемый нет. терминов | 5 |
| Последовательность | Числа Ферма |
| Первые сроки | 3 , 5 , 17 , 257 , 65537 |
| Самый большой известный термин | 65537 |
| ОЭИС Индекс | А019434 |
В математике число Ферма , названное в честь Пьера де Ферма , первого известного человека, изучавшего их, представляет собой целое положительное число вида: где n — неотрицательное целое число. Первые несколько чисел Ферма: 3 , 5 , 17 , 257 , 65537 , 4294967297, 18446744073709551617, ... (последовательность A000215 в OEIS ).
Если 2 к + 1 — простое число и k > 0 , то само k должно быть степенью 2, [1] итак 2 к + 1 — число Ферма; такие простые числа называются простыми числами Ферма . По состоянию на 2023 год [update]единственные известные простые числа Ферма — это F 0 = 3 , F 1 = 5 , F 2 = 17 , F 3 = 257 и F 4 = 65537 (последовательность A019434 в OEIS ).
Основные свойства
[ редактировать ]Числа Ферма удовлетворяют следующим рекуррентным соотношениям :
для n ≥ 1,
для n ≥ 2 . Каждое из этих соотношений можно доказать методом математической индукции . Из второго уравнения мы можем вывести теорему Гольдбаха (названную в честь Кристиана Гольдбаха ): никакие два числа Ферма не имеют общего целого множителя, большего 1 . Чтобы убедиться в этом, предположим, что ≤ i < j и Fi и F j 0 имеют общий множитель a > 1 . Тогда a делит оба
и Fj ; следовательно, a делит их разницу, 2. Поскольку a > 1 , это приводит к a = 2 . Это противоречие , поскольку каждое число Ферма явно нечетно. В качестве следствия получаем еще одно доказательство бесконечности простых чисел: для каждого F n выбираем простой множитель p n ; тогда последовательность { pn } является бесконечной последовательностью различных простых чисел.
Дополнительные свойства
[ редактировать ]- Ни одно простое число Ферма не может быть выражено как разность двух p -х степеней, где p — нечетное простое число.
- За исключением F 0 и F 1 , последняя цифра числа Ферма равна 7.
- Сумма обратных величин всех чисел Ферма (последовательность A051158 в OEIS ) иррациональна . ( Соломон В. Голомб , 1963)
Первичность
[ редактировать ]Числа Ферма и простые числа Ферма были впервые изучены Пьером де Ферма, который предположил , что все числа Ферма являются простыми. Действительно, легко показать, что первые пять чисел Ферма F 0 , ..., F 4 являются простыми. Гипотеза Ферма была опровергнута Леонардом Эйлером в 1732 году, когда он показал, что
Эйлер доказал, что каждый фактор F n должен иметь вид k 2 п +1 + 1 (позже улучшено до k 2 п +2 + 1 Лукаса 2 ) для n ≥ .
То, что 641 является фактором F 5, можно вывести из равенств 641 = 2 7 × 5 + 1 и 641 = 2 4 + 5 4 . Из первого равенства следует, что 2 7 × 5 ≡ −1 (по модулю 641), и поэтому (возводим в четвертую степень) что 2 28 × 5 4 ≡ 1 (по модулю 641). С другой стороны, из второго равенства следует, что 5 4 ≡ −2 4 (мод 641). Эти сравнения означают, что 2 32 ≡ −1 (по модулю 641).
Ферма, вероятно, знал о форме множителей, позже доказанных Эйлером, поэтому кажется любопытным, что ему не удалось выполнить простой расчет для нахождения множителя. [2] Одно из распространенных объяснений состоит в том, что Ферма допустил вычислительную ошибку.
не существует Других известных простых чисел Ферма F n с n > 4 , но мало что известно о числах Ферма для больших n . [3] Фактически, каждая из следующих проблем является открытой проблемой:
- Является ли F n составным для всех n > 4 ?
- Существует ли бесконечно много простых чисел Ферма? ( Эйзенштейн 1844 г. [4] )
- Существует ли бесконечно много составных чисел Ферма?
- Существует ли число Ферма, не свободное от квадратов ?
По состоянию на 2024 год [update], известно, что F n является составным для 5 ≤ n ≤ 32 , хотя из них полные факторизации F n известны только для 0 ≤ n ≤ 11 не известны простые множители , а для n = 20 и n = 24 . . [5] Наибольшее известное составное число Ферма — F 18233954 , а его простой делитель 7 × 2. 18233956 +1 был обнаружен в октябре 2020 года.
Эвристические аргументы
[ редактировать ]Эвристика предполагает, что F 4 — последнее простое число Ферма.
Теорема о простых числах что случайное целое число в подходящем интервале вокруг N является простым с вероятностью 1 / ln N. подразумевает , Если использовать эвристику, согласно которой число Ферма является простым с той же вероятностью, что и случайное целое число его размера, и что F 5 , ..., F 32 являются составными, то ожидаемое количество простых чисел Ферма, превышающее F 4 (или, что эквивалентно, , за F 32 ) должно быть
Это число можно интерпретировать как верхнюю границу вероятности существования простого числа Ферма, превосходящего F 4 .
Этот аргумент не является строгим доказательством. Во-первых, предполагается, что числа Ферма ведут себя «случайно», но факторы чисел Ферма обладают особыми свойствами. Боклан и Конвей опубликовали более точный анализ, показывающий, что вероятность существования еще одного простого числа Ферма составляет менее одного на миллиард. [6]
Андерс Бьорн и Ханс Ризель оценили количество квадратных факторов чисел Ферма, начиная с F 5 , как
другими словами, вряд ли существуют какие-либо несвободные от квадратов числа Ферма и вообще квадратные коэффициенты очень редки для больших n . [7]
Эквивалентные условия
[ редактировать ]Позволять быть n-м числом Ферма. Тест Пепена утверждает, что для n > 0
- является простым тогда и только тогда, когда
Выражение можно оценить по модулю путем повторного возведения в квадрат . Это делает тест быстрым алгоритмом с полиномиальным временем . Но числа Ферма растут настолько быстро, что лишь немногие из них можно проверить за разумный промежуток времени и пространства.
Есть несколько тестов для чисел вида k 2 м + 1 , например, факторы чисел Ферма, для простоты.
- Теорема Прота (1878 г.). Пусть N = k 2 м + 1 при нечетном k < 2 м . Если существует целое число a такое, что
- затем является простым. Обратно, если приведенное выше сравнение не выполнено и, кроме того,
- (См. символ Якоби )
- затем является составным.
Если N = F n > 3 , то указанный выше символ Якоби всегда равен −1 для a = 3 , и этот частный случай теоремы Прота известен как тест Пепина . Хотя тест Пепена и теорема Прота были реализованы на компьютерах для доказательства составности некоторых чисел Ферма, ни один из тестов не дает конкретного нетривиального фактора. Фактически, для n = 20 и 24 не известны конкретные простые множители.
Факторизация
[ редактировать ]Из-за размера чисел Ферма их сложно факторизовать или даже проверить на простоту. Тест Пепена дает необходимое и достаточное условие простоты чисел Ферма и может быть реализован на современных компьютерах. Метод эллиптических кривых — это быстрый метод нахождения малых простых делителей чисел. Проект распределенных вычислений Fermatsearch обнаружил некоторые факторы чисел Ферма. Программа proth.exe Ива Галло использовалась для поиска факторов больших чисел Ферма. Эдуард Люка , улучшая вышеупомянутый результат Эйлера, доказал в 1878 году, что каждый фактор числа Ферма , где n не менее 2, имеет вид (см. число Прота ), где k — целое положительное число. Само по себе это позволяет легко доказать простоту известных простых чисел Ферма.
Факторизация первых 12 чисел Ферма:
Ф 0 = 2 1 + 1 = 3 простое Ф 1 = 2 2 + 1 = 5 - простое число FФ2 = 2 4 + 1 = 17 - простое число F 3 = 2 8 + 1 = 257 — простое число FF4 = 2 16 + 1 = 65 537 — самое большое известное простое число Ферма. Ф 5 = 2 32 + 1 = 4,294,967,297 = 641 × 6700417 (полностью учтено 1732 г.) [8] ) Ф 6 = 2 64 + 1 = 18 446 744 073 709 551 617 (20 цифр) = 274 177 × 67 280 421 310 721 (14 цифр) (полностью факторизованный 1855 г.) FF7 = 2 128 + 1 = 340 282 366 920 938 463 463 374 607 431 768 211 457 (39 цифр) = 59 649 589 127 497 217 (17 цифр) × 5 704 689 200 685 129 054 721 (22 цифры) (полностью факторизованы в 1970 г.) Ф 8 = 2 256 + 1 = 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,
639 937 (78 цифр)= 1 238 926 361 552 897 (16 цифр) ×
93 461 639 715 357 977 769 163 558 199 606 896 584 051 237 541 638 188 580 280 321 (62 цифры) (полностью факторизованы в 1980 г.)FF9 = 2 512 + 1 = 13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,393,377,723,561,443,721,764,0
30,073,546,976,801,874,298,166,903,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,6
49 006 084 097 (155 цифр)= 2 424 833 × 7 455 602 825 647 884 208 337 395 736 200 454 918 783 366 342 657 (49 цифр) ×
741,640,062,627,530,801,524,787,141,901,937,474,059,940,781,097,519,023,905,821,316,144,415,759,
504 705 008 092 818 711 693 940 737 (99 цифр) (полностью факторизованы в 1990 г.)Ф 10 = 2 1024 + 1 = 179 769 313 486 231 590 772 930...304 835 356 329 624 224 137 217 (309 цифр) = 45 592 577 × 6 487 031 809 × 4 659 775 785 220 018 543 264 560 743 076 778 192 897 (40 цифр) ×
130 439 874 405 488 189 727 484... 806 217 820 753 127 014 424 577 (252 цифры) (полностью факторизованы в 1995 г.)Ф 11 = 2 2048 + 1 = 32 317 006 071 311 007 300 714,8...193 555 853 611 059 596 230 657 (617 цифр) = 319 489 × 974 849 × 167 988 556 341 760 475 137 (21 цифра) × 3 560 841 906 445 833 920 513 (22 цифры) ×
173 462 447 179 147 555 430 258 ... 491 382 441 723 306 598 834 177 (564 цифры) (полностью факторизованы в 1988 г.)
По состоянию на апрель 2023 г. [update] только F0 – F11 полностью учтены . [5] Проект распределенных вычислений Fermat Search занимается поиском новых факторов чисел Ферма. [9] Набор всех факторов Ферма — A050922 (или, отсортированный, A023394 ) в OEIS .
Следующие факторы чисел Ферма были известны до 1950 года (с тех пор цифровые компьютеры помогли найти больше факторов):
| Год | Искатель | Число Ферма | Фактор |
|---|---|---|---|
| 1732 | Эйлер | ||
| 1732 | Эйлер | (полностью учтено) | |
| 1855 | Клаузен | ||
| 1855 | Клаузен | (полностью учтено) | |
| 1877 | Первушин | ||
| 1878 | Первушин | ||
| 1886 | Зильхофф | ||
| 1899 | Каннингем | ||
| 1899 | Каннингем | ||
| 1903 | западный | ||
| 1903 | западный | ||
| 1903 | западный | ||
| 1903 | западный | ||
| 1903 | Каллен | ||
| 1906 | Морхед | ||
| 1925 | Крайчик |
По состоянию на июль 2023 г. [update]Известно 368 простых делителей чисел Ферма и 324 числа Ферма, которые являются составными. [5] Каждый год обнаруживается несколько новых факторов Ферма. [10]
Псевдопростые числа и числа Ферма
[ редактировать ]Подобно составным числам вида 2 п − 1, каждое составное число Ферма является сильным псевдопростым числом по основанию 2. Это связано с тем, что все сильные псевдопростые числа по основанию 2 также являются псевдопростыми числами Ферма , т. е.
для всех чисел Ферма. [11]
В 1904 году Чиполла показал, что произведение по крайней мере двух различных простых или составных чисел Ферма будет псевдопростым числом Ферма по основанию 2 тогда и только тогда, когда . [12]
Другие теоремы о числах Ферма
[ редактировать ]Лемма. — Если n — целое положительное число,
Теорема — Если нечетное простое число, то это степень 2.
Если — целое положительное число, но не степень двойки, оно должно иметь нечетный простой делитель , и мы можем написать где .
По предыдущей лемме для натурального числа ,
где означает «равномерно делит». Замена , и и используя это странно,
и таким образом
Потому что , отсюда следует, что не является простым. Поэтому, в противопоставлении должна быть степенью 2.
Теорема : Простое число Ферма не может быть простым числом Вифериха .
Мы показываем, если является простым числом Ферма (и, следовательно, по вышесказанному m является степенью двойки), то сравнение не держит.
С мы можем написать . Если данное сравнение выполнено, то , и поэтому
Следовательно , и поэтому . Это приводит к , что невозможно, поскольку .
Теорема ( Эдуард Люка ) — Любой простой делитель p числа имеет форму всякий раз, когда n > 1 .
Пусть G p обозначает группу ненулевых целых чисел по модулю p при умножении , которая имеет порядок p − 1 . Заметим, что 2 (строго говоря, ее образ по модулю p ) имеет мультипликативный порядок, равный в G p (поскольку это квадрат что равно −1 по модулю F n ), так что по Лагранжа теореме p − 1 делится на и p имеет вид для некоторого целого числа k , как знал Эйлер . Эдуард Лукас пошел еще дальше. Поскольку n > 1 , простое число p выше соответствует 1 по модулю 8. Следовательно (как было известно Карлу Фридриху Гауссу ), 2 является квадратичным вычетом по модулю p , то есть существует целое число a такое, что Тогда образ a имеет порядок в группе G p и (снова используя теорему Лагранжа) p − 1 делится на и p имеет вид для некоторого целого числа s .
На самом деле, непосредственно видно, что 2 — квадратичный вычет по модулю p , поскольку
Поскольку нечетная степень 2 является квадратичным вычетом по модулю p , то же самое относится и к 2.
Число Ферма не может быть совершенным числом или частью пары дружественных чисел . ( Лука 2000 )
Ряд обратных всех простых делителей чисел Ферма сходится . ( Кржижек, Лука и Сомер, 2002 г. )
Если н н + 1 — простое число, существует целое число m такое, что n = 2 2 м . Уравнение н н + 1 = Ф (2 м + м ) имеет место в таком случае. [13] [14]
Пусть наибольший простой делитель числа Fn Ферма равен P ( Fn ) . Затем,
Связь с конструируемыми многоугольниками
[ редактировать ]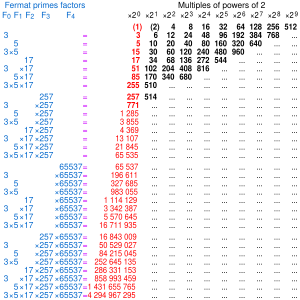
Карл Фридрих Гаусс развил теорию гауссовских периодов в своих « Арифметических исследованиях» и сформулировал достаточное условие возможности построения правильных многоугольников. Гаусс заявил, что это условие также необходимо . [15] но так и не опубликовал доказательство. Пьер Ванцель дал полное доказательство необходимости в 1837 году. Результат известен как теорема Гаусса – Ванцеля :
- n - сторонний правильный многоугольник можно построить с помощью циркуля и линейки тогда и только тогда, когда n является либо степенью 2, либо произведением степени 2 и различных простых чисел Ферма: другими словами, тогда и только тогда, когда n имеет вид п = 2 к или п = 2 к p 1 p 2 ... p s , где k , s — целые неотрицательные числа, а pi — различные простые числа Ферма.
Целое положительное число n имеет указанную выше форму тогда и только тогда, когда его точка φ ( n ) является степенью 2.
Применение чисел Ферма
[ редактировать ]Генерация псевдослучайных чисел
[ редактировать ]Простые числа Ферма особенно полезны при создании псевдослучайных последовательностей чисел в диапазоне 1, ..., N , где N — степень 2. Наиболее распространенный метод — взять любое начальное значение от 1 до P − 1 . где P — простое число Ферма. Теперь умножьте это на число A , которое больше квадратного корня из P и является первообразным корнем по модулю P (т. е. оно не является квадратичным вычетом ). Затем возьмите результат по P. модулю Результатом является новое значение ГСЧ.
- (см. линейный конгруэнтный генератор , RANDU )
Это полезно в информатике, поскольку большинство структур данных имеют элементы с двумя Х возможные значения. Например, байт имеет 256 (2 8 ) возможные значения (0–255). Следовательно, чтобы заполнить байт или байты случайными значениями, можно использовать генератор случайных чисел, который выдает значения от 1 до 256, при этом байт принимает выходное значение -1. По этой причине очень большие простые числа Ферма представляют особый интерес для шифрования данных. Этот метод выдает только псевдослучайные значения, так как после P - 1 повторений последовательность повторяется. Плохо выбранный множитель может привести к повторению последовательности раньше, чем P − 1 .
Обобщенные числа Ферма
[ редактировать ]Числа формы с a , b любые взаимно простые целые числа, a > b > 0 , называются обобщенными числами Ферма . Нечетное простое число p является обобщенным числом Ферма тогда и только тогда, когда p конгруэнтно 1 (mod 4) . (Здесь мы рассматриваем только случай n > 0 , поэтому 3 = это не контрпример.)
Пример вероятного простого числа этой формы — 1215. 131072 + 242 131072 (найдено Келлен Шентон). [16]
По аналогии с обычными числами Ферма принято писать обобщенные числа Ферма вида как F n ( а ). Например, в этой записи число 100 000 001 будет записано как F 3 (10). В дальнейшем мы ограничимся простыми числами такого вида: , такие простые числа называются «простыми числами Ферма по основанию a ». Конечно, эти простые числа существуют только в том случае, a четно если .
Если нам требуется n > 0 , то четвертая проблема Ландау спрашивает, существует ли бесконечно много обобщенных простых чисел Ферма F n ( a ).
Обобщенные простые числа Ферма вида F n ( a )
[ редактировать ]Из-за простоты доказательства своей простоты обобщенные простые числа Ферма в последние годы стали темой исследований в области теории чисел. Многие из крупнейших известных сегодня простых чисел являются обобщенными простыми числами Ферма.
Обобщенные числа Ферма могут быть простыми только при четном a , потому что если a нечетно, то каждое обобщенное число Ферма будет делиться на 2. Наименьшее простое число с является , или 30 32 + 1. Кроме того, мы можем определить «полуобобщенные числа Ферма» для нечетной базы, полуобобщенное число Ферма для базы a (для нечетного a ) равно , и также следует ожидать, что для каждой нечетной базы будет только конечное число полуобобщенных простых чисел Ферма.
В этом списке обобщенные числа Ферма ( ) до четного a являются , для нечетного a , они . Если a — совершенная степень с нечетным показателем (последовательность A070265 в OEIS ), то все обобщенные числа Ферма могут быть разложены на алгебраические множители, поэтому они не могут быть простыми.
Видеть [17] [18] для четных оснований до 1000, и [19] для нечетных оснований. Для наименьшего числа такой, что является простым, см. OEIS : A253242 .
| цифры такой, что является простым | цифры такой, что является простым | цифры такой, что является простым | цифры такой, что является простым | ||||
|---|---|---|---|---|---|---|---|
| 2 | 0, 1, 2, 3, 4, ... | 18 | 0, ... | 34 | 2, ... | 50 | ... |
| 3 | 0, 1, 2, 4, 5, 6, ... | 19 | 1, ... | 35 | 1, 2, 6, ... | 51 | 1, 3, 6, ... |
| 4 | 0, 1, 2, 3, ... | 20 | 1, 2, ... | 36 | 0, 1, ... | 52 | 0, ... |
| 5 | 0, 1, 2, ... | 21 | 0, 2, 5, ... | 37 | 0, ... | 53 | 3, ... |
| 6 | 0, 1, 2, ... | 22 | 0, ... | 38 | ... | 54 | 1, 2, 5, ... |
| 7 | 2, ... | 23 | 2, ... | 39 | 1, 2, ... | 55 | ... |
| 8 | (никто) | 24 | 1, 2, ... | 40 | 0, 1, ... | 56 | 1, 2, ... |
| 9 | 0, 1, 3, 4, 5, ... | 25 | 0, 1, ... | 41 | 4, ... | 57 | 0, 2, ... |
| 10 | 0, 1, ... | 26 | 1, ... | 42 | 0, ... | 58 | 0, ... |
| 11 | 1, 2, ... | 27 | (никто) | 43 | 3, ... | 59 | 1, ... |
| 12 | 0, ... | 28 | 0, 2, ... | 44 | 4, ... | 60 | 0, ... |
| 13 | 0, 2, 3, ... | 29 | 1, 2, 4, ... | 45 | 0, 1, ... | 61 | 0, 1, 2, ... |
| 14 | 1, ... | 30 | 0, 5, ... | 46 | 0, 2, 9, ... | 62 | ... |
| 15 | 1, ... | 31 | ... | 47 | 3, ... | 63 | ... |
| 16 | 0, 1, 2, ... | 32 | (никто) | 48 | 2, ... | 64 | (никто) |
| 17 | 2, ... | 33 | 0, 3, ... | 49 | 1, ... | 65 | 1, 2, 5, ... |
Для наименьшей четной базы a такой, что является простым, см. OEIS : A056993 .
| основания такие , что является простым (учитывайте только четное a ) | OEIS Последовательность | |
|---|---|---|
| 0 | 2, 4, 6, 10, 12, 16, 18, 22, 28, 30, 36, 40, 42, 46, 52, 58, 60, 66, 70, 72, 78, 82, 88, 96, 100, 102, 106, 108, 112, 126, 130, 136, 138, 148, 150, ... | А006093 |
| 1 | 2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56, 66, 74, 84, 90, 94, 110, 116, 120, 124, 126, 130, 134, 146, 150, 156, 160, 170, 176, 180, 184, ... | А005574 |
| 2 | 2, 4, 6, 16, 20, 24, 28, 34, 46, 48, 54, 56, 74, 80, 82, 88, 90, 106, 118, 132, 140, 142, 154, 160, 164, 174, 180, 194, 198, 204, 210, 220, 228, ... | А000068 |
| 3 | 2, 4, 118, 132, 140, 152, 208, 240, 242, 288, 290, 306, 378, 392, 426, 434, 442, 508, 510, 540, 542, 562, 596, 610, 664, 680, 682, 732, 782, ... | А006314 |
| 4 | 2, 44, 74, 76, 94, 156, 158, 176, 188, 198, 248, 288, 306, 318, 330, 348, 370, 382, 396, 452, 456, 470, 474, 476, 478, 560, 568, 598, 642, ... | А006313 |
| 5 | 30, 54, 96, 112, 114, 132, 156, 332, 342, 360, 376, 428, 430, 432, 448, 562, 588, 726, 738, 804, 850, 884, 1068, 1142, 1198, 1306, 1540, 1568, ... | А006315 |
| 6 | 102, 162, 274, 300, 412, 562, 592, 728, 1084, 1094, 1108, 1120, 1200, 1558, 1566, 1630, 1804, 1876, 2094, 2162, 2164, 2238, 2336, 2388, ... | А006316 |
| 7 | 120, 190, 234, 506, 532, 548, 960, 1738, 1786, 2884, 3000, 3420, 3476, 3658, 4258, 5788, 6080, 6562, 6750, 7692, 8296, 9108, 9356, 9582, ... | А056994 |
| 8 | 278, 614, 892, 898, 1348, 1494, 1574, 1938, 2116, 2122, 2278, 2762, 3434, 4094, 4204, 4728, 5712, 5744, 6066, 6508, 6930, 7022, 7332, ... | А056995 |
| 9 | 46, 1036, 1318, 1342, 2472, 2926, 3154, 3878, 4386, 4464, 4474, 4482, 4616, 4688, 5374, 5698, 5716, 5770, 6268, 6386, 6682, 7388, 7992, ... | А057465 |
| 10 | 824, 1476, 1632, 2462, 2484, 2520, 3064, 3402, 3820, 4026, 6640, 7026, 7158, 9070, 12202, 12548, 12994, 13042, 15358, 17646, 17670, ... | А057002 |
| 11 | 150, 2558, 4650, 4772, 11272, 13236, 15048, 23302, 26946, 29504, 31614, 33308, 35054, 36702, 37062, 39020, 39056, 43738, 44174, 45654, ... | А088361 |
| 12 | 1534, 7316, 17582, 18224, 28234, 34954, 41336, 48824, 51558, 51914, 57394, 61686, 62060, 89762, 96632, 98242, 100540, 101578, 109696, ... | А088362 |
| 13 | 30406, 71852, 85654, 111850, 126308, 134492, 144642, 147942, 150152, 165894, 176206, 180924, 201170, 212724, 222764, 225174, 241600, ... | А226528 |
| 14 | 67234, 101830, 114024, 133858, 162192, 165306, 210714, 216968, 229310, 232798, 422666, 426690, 449732, 462470, 468144, 498904, 506664, ... | А226529 |
| 15 | 70906, 167176, 204462, 249830, 321164, 330716, 332554, 429370, 499310, 524552, 553602, 743788, 825324, 831648, 855124, 999236, 1041870, ... | А226530 |
| 16 | 48594, 108368, 141146, 189590, 255694, 291726, 292550, 357868, 440846, 544118, 549868, 671600, 843832, 857678, 1024390, 1057476, 1087540, ... | А251597 |
| 17 | 62722, 130816, 228188, 386892, 572186, 689186, 909548, 1063730, 1176694, 1361244, 1372930, 1560730, 1660830, 1717162, 1722230, 1766192, ... | А253854 |
| 18 | 24518, 40734, 145310, 361658, 525094, 676754, 773620, 1415198, 1488256, 1615588, 1828858, 2042774, 2514168, 2611294, 2676404, 3060772, ... | А244150 |
| 19 | 75898, 341112, 356926, 475856, 1880370, 2061748, 2312092, 2733014, 2788032, 2877652, 2985036, 3214654, 3638450, 4896418, 5897794, ... | А243959 |
| 20 | 919444, 1059094, 1951734, 1963736, ... | А321323 |
Наименьшие основания b=b(n) такие, что b 2 н + 1 (для данного n= 0,1,2,... ) является простым числом.
- 2, 2, 2, 2, 2, 30, 102, 120, 278, 46, 824, 150, 1534, 30406, 67234, 70906, 48594, 62722, 24518, 75898, 919444, ... (последовательность A056993 в ОЭИС )
Обратно, наименьшее k=k(n) такое, что (2 n ) к + 1 (для заданного n ) является простым, являются
- 1, 1, 1, 0, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 0, 4, 1, ... (Следующий член неизвестен) (последовательность A079706 в OEIS OEIS (см. также A228101 : A084712 и OEIS : ) )
Можно использовать более сложную теорию, чтобы предсказать количество оснований, для которых будет простым для фиксированного . Можно примерно ожидать, что количество обобщенных простых чисел Ферма уменьшится вдвое, поскольку увеличивается на 1.
Обобщенные простые числа Ферма вида F n ( a , b )
[ редактировать ]Также возможно построить обобщенные простые числа Ферма вида . Как и в случае, когда b = 1, числа этой формы всегда будут делиться на 2, если a + b четно, но все же возможно определить обобщенные простые числа полуферма этого типа. Для наименьшего простого числа формы (для нечетных ), см. также OEIS : A111635 .
| цифры такой, что является простым [20] [7] | ||
|---|---|---|
| 2 | 1 | 0, 1, 2, 3, 4, ... |
| 3 | 1 | 0, 1, 2, 4, 5, 6, ... |
| 3 | 2 | 0, 1, 2, ... |
| 4 | 1 | 0, 1, 2, 3, ... (эквивалентно ) |
| 4 | 3 | 0, 2, 4, ... |
| 5 | 1 | 0, 1, 2, ... |
| 5 | 2 | 0, 1, 2, ... |
| 5 | 3 | 1, 2, 3, ... |
| 5 | 4 | 1, 2, ... |
| 6 | 1 | 0, 1, 2, ... |
| 6 | 5 | 0, 1, 3, 4, ... |
| 7 | 1 | 2, ... |
| 7 | 2 | 1, 2, ... |
| 7 | 3 | 0, 1, 8, ... |
| 7 | 4 | 0, 2, ... |
| 7 | 5 | 1, 4, |
| 7 | 6 | 0, 2, 4, ... |
| 8 | 1 | (никто) |
| 8 | 3 | 0, 1, 2, ... |
| 8 | 5 | 0, 1, 2, |
| 8 | 7 | 1, 4, ... |
| 9 | 1 | 0, 1, 3, 4, 5, ... (эквивалентно ) |
| 9 | 2 | 0, 2, ... |
| 9 | 4 | 0, 1, ... (эквивалентно ) |
| 9 | 5 | 0, 1, 2, ... |
| 9 | 7 | 2, ... |
| 9 | 8 | 0, 2, 5, ... |
| 10 | 1 | 0, 1, ... |
| 10 | 3 | 0, 1, 3, ... |
| 10 | 7 | 0, 1, 2, ... |
| 10 | 9 | 0, 1, 2, ... |
| 11 | 1 | 1, 2, ... |
| 11 | 2 | 0, 2, ... |
| 11 | 3 | 0, 3, ... |
| 11 | 4 | 1, 2, ... |
| 11 | 5 | 1, ... |
| 11 | 6 | 0, 1, 2, ... |
| 11 | 7 | 2, 4, 5, ... |
| 11 | 8 | 0, 6, ... |
| 11 | 9 | 1, 2, ... |
| 11 | 10 | 5, ... |
| 12 | 1 | 0, ... |
| 12 | 5 | 0, 4, ... |
| 12 | 7 | 0, 1, 3, ... |
| 12 | 11 | 0, ... |
Самые большие известные обобщенные простые числа Ферма
[ редактировать ]Ниже приводится список пяти крупнейших известных обобщенных простых чисел Ферма. [21] Весь топ-5 обнаружен участниками проекта PrimeGrid .
| Классифицировать | Простое число | Обобщенное обозначение Ферма | Количество цифр | Дата открытия | исх. |
|---|---|---|---|---|---|
| 1 | 1963736 1048576 + 1 | Ф 20 (1963736) | 6,598,776 | Сентябрь 2022 г. | [22] |
| 2 | 1951734 1048576 + 1 | Ф 20 (1951734) | 6,595,985 | август 2022 г. | [23] |
| 3 | 1059094 1048576 + 1 | Ф 20 (1059094) | 6,317,602 | ноябрь 2018 г. | [24] |
| 4 | 919444 1048576 + 1 | Ф 20 (919444) | 6,253,210 | Сентябрь 2017 г. | [25] |
| 5 | 81 × 2 20498148 + 1 | Ф2 2 (3× 5124537 ) | 6,170,560 | июнь 2023 г. | [26] |
На страницах Prime Pages можно найти текущие 100 лучших обобщенных простых чисел Ферма .
См. также
[ редактировать ]- Конструируемый многоугольник : какие правильные многоугольники можно построить, частично зависит от простых чисел Ферма.
- Двойная экспоненциальная функция
- Теорема Лукаса
- Мерсенн премьер
- Пьерпон Прайм
- Тест на примитивность
- Теорема Прота
- Псевдопростой
- Число Серпинского
- Последовательность Сильвестра
Примечания
[ редактировать ]- ^ Для любого положительного нечетного числа , где .
- ^ Кржижек, Лука и Сомер 2001 , стр. 38, замечание 4.15.
- ^ Крис Колдуэлл, «Prime Links++: специальные формы». Архивировано 24 декабря 2013 г. в Wayback Machine на The Prime Pages .
- ^ Рибенбойм 1996 , с. 88.
- ^ Jump up to: Перейти обратно: а б с Келлер, Уилфрид (18 января 2021 г.), «Простые факторы чисел Ферма» , ProthSearch.com , получено 19 января 2021 г.
- ^ Боклан, Кент Д.; Конвей, Джон Х. (2017). «Ожидайте не более одной миллиардной части нового числа Ферма!». Математический интеллект . 39 (1): 3–5. arXiv : 1605.01371 . дои : 10.1007/s00283-016-9644-3 . S2CID 119165671 .
- ^ Jump up to: Перейти обратно: а б Бьёрн, Андерс; Ризель, Ганс (1998). «Факторы обобщенных чисел Ферма» . Математика вычислений . 67 (221): 441–446. дои : 10.1090/S0025-5718-98-00891-6 . ISSN 0025-5718 .
- ^ Сандифер, Эд. «Как это сделал Эйлер» (PDF) . МАА Онлайн . Математическая ассоциация Америки. Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 13 июня 2020 г.
- ^ ":: FERMATSEARCH .ORG :: Домашняя страница" . www.fermatsearch.org . Проверено 7 апреля 2018 г.
- ^ "::FERMATSEARCH.ORG::Новости" . www.fermatsearch.org . Проверено 7 апреля 2018 г.
- ^ Шредер, MR (2006). Теория чисел в науке и коммуникации: с приложениями в криптографии, физике, цифровой информации, вычислениях и самоподобии . Серия Springer по информационным наукам (4-е изд.). Берлин ; Нью-Йорк: Спрингер. п. 216. ИСБН 978-3-540-26596-2 . OCLC 61430240 .
- ^ Крижек, Михал; Лука, Флориан; Сомер, Лоуренс (14 марта 2013 г.). 17 лекций о числах Ферма: от теории чисел к геометрии . Springer Science & Business Media. ISBN 9780387218502 . Проверено 7 апреля 2018 г. - через Google Книги.
- ^ Йеппе Стиг Нильсен, «S(n) = n^n + 1» .
- ^ Вайсштейн, Эрик В. «Число Серпинского первого рода» . Математический мир .
- ^ Гаусс, Карл Фридрих (1966). Арифметические исследования . Нью-Хейвен и Лондон: Издательство Йельского университета. стр. 458–460 . Проверено 25 января 2023 г.
- ^ Лучшие записи PRP, поиск x^131072+y^131072 , авторы Анри и Рено Лифшиц.
- ^ «Обобщенные простые числа Ферма» . jeppesn.dk . Проверено 7 апреля 2018 г.
- ^ «Обобщенные простые числа Ферма по основаниям до 1030» . noprimeleftbehind.net . Проверено 7 апреля 2018 г.
- ^ «Обобщенные простые числа Ферма в нечетных основаниях» . Fermatquotient.com . Проверено 7 апреля 2018 г.
- ^ «Оригинальные факторы GFN» . www.prothsearch.com .
- ^ Колдуэлл, Крис К. «Двадцатка лучших: обобщенный Ферма» . Главные страницы . Проверено 11 июля 2019 г.
- ^ 1963736 1048576 + 1
- ^ 1951734 1048576 + 1
- ^ 1059094 1048576 + 1
- ^ 919444 1048576 + 1
- ^ 81*2 20498148 + 1
Ссылки
[ редактировать ]- Голомб, SW (1 января 1963 г.), «О сумме обратных чисел Ферма и связанных с ними иррациональностях», Canadian Journal of Mathematics , 15 : 475–478, doi : 10.4153/CJM-1963-051-0 , S2CID 123138118
- Гричук А.; Лука Ф. и Войтович М. (2001), «Еще одна заметка о величайших простых факторах чисел Ферма», Юго-Восточноазиатский математический бюллетень , 25 (1): 111–115, doi : 10.1007/s10012-001-0111 -4 , S2CID 122332537
- Гай, Ричард К. (2004), Нерешенные проблемы теории чисел , Сборники задач по математике, том. 1 (3-е изд.), Нью-Йорк: Springer Verlag , стр. A3, A12, B21, ISBN. 978-0-387-20860-2
- Кржижек, Михал; Лука, Флориан и Сомер, Лоуренс (2001), 17 лекций по числам Ферма: от теории чисел к геометрии , книги CMS по математике, том. 10, Нью-Йорк: Спрингер, ISBN. 978-0-387-95332-8 - Эта книга содержит обширный список литературы.
- Кржижек, Михал; Лука, Флориан и Сомер, Лоуренс (2002), «О сходимости рядов обратных простых чисел, связанных с числами Ферма», Journal of Number Theory , 97 (1): 95–112, doi : 10.1006/jnth.2002.2782
- Лука, Флориан (2000), «Антисоциальное число Ферма» , American Mathematical Monthly , 107 (2): 171–173, doi : 10.2307/2589441 , JSTOR 2589441
- Рибенбойм, Пауло (1996), Новая книга рекордов простых чисел (3-е изд.), Нью-Йорк: Springer, ISBN 978-0-387-94457-9
- Робинсон, Рафаэль М. (1954), «Числа Мерсенна и Ферма», Труды Американского математического общества , 5 (5): 842–846, doi : 10.2307/2031878 , JSTOR 2031878
- Ябута, М. (2001), «Простое доказательство теоремы Кармайкла о примитивных делителях» (PDF) , Fibonacci Quarterly , 39 : 439–443, заархивировано (PDF) из оригинала 9 октября 2022 г.
Внешние ссылки
[ редактировать ]- Крис Колдуэлл, The Prime Glossary: число Ферма на The Prime Pages .
- Луиджи Морелли, История чисел Ферма
- Джон Косгрейв, Объединение чисел Мерсенна и Ферма
- Уилфрид Келлер, Простые факторы чисел Ферма
- Вайсштейн, Эрик В. «Число Ферма» . Математический мир .
- Вайсштейн, Эрик В. «Ферма Прайм» . Математический мир .
- Вайсштейн, Эрик В. «Обобщенное число Ферма» . Математический мир .
- Ив Галло, Обобщенный поиск простых чисел Ферма
- Марк С. Манасс, Полная факторизация девятого числа Ферма (исходное объявление)
- Пейтон Хейслетт, самое известное объявление обобщенного простого числа Ферма









































































































