Параметрическое уравнение

В математике параметрическое уравнение определяет группу величин как функции одной или нескольких независимых переменных, называемых параметрами . ^[1] Параметрические уравнения обычно используются для выражения координат точек, составляющих геометрический объект, такой как кривая или поверхность , называемых параметрической кривой и параметрической поверхностью соответственно. В таких случаях уравнения в совокупности называются параметрическим представлением , ^[2] или параметрическая система , ^[3] или параметризация (альтернативно называемая параметризацией ) объекта. ^[1]^[4]^[5]

Например, уравнения ${\begin{aligned}x&=\cos t\\y&=\sin t\end{aligned}}$ сформируйте параметрическое представление единичного круга , где $t$ — параметр: Точка $(x, y)$ находится на единичном круге тогда и только тогда, когда существует значение $t$ такое, что эти два уравнения порождают эту точку. Иногда параметрические уравнения для отдельных скалярных выходных переменных объединяются в одно параметрическое уравнение в векторах :

$(x,y)=(\cos t,\sin t).$

Параметрические представления, как правило, неуникальны (см. раздел «Примеры в двух измерениях» ниже), поэтому одни и те же величины могут быть выражены с помощью ряда различных параметризаций. ^[1]

Помимо кривых и поверхностей, параметрические уравнения могут описывать многообразия и алгебраические многообразия более высокой размерности , при этом число параметров равно размерности многообразия или многообразия, а число уравнений равно размерности пространства, в котором рассматривается многообразие или многообразие (для кривых размерность один и один используется параметр, для поверхностей размерность два и два параметра и т. д.).

Параметрические уравнения обычно используются в кинематике , где траектория объекта представляется уравнениями, зависящими от времени как параметра. Из-за этого приложения один параметр часто обозначается $t$ ; однако параметры могут представлять другие физические величины (например, геометрические переменные) или могут выбираться произвольно для удобства. Параметризации не уникальны; одну и ту же кривую можно задать более чем одним набором параметрических уравнений. ^[6]

Приложения

Кинематика

В кинематике траектории объектов в пространстве обычно описываются как параметрические кривые, где каждая пространственная координата явно зависит от независимого параметра (обычно времени). При таком использовании набор параметрических уравнений для координат объекта в совокупности представляет собой векторную функцию положения. Такие параметрические кривые затем можно почленно интегрировать и дифференцировать . Таким образом, если положение частицы описывается параметрически как $\mathbf {r} (t)=(x(t),y(t),z(t))\,,$

то его скорость можно найти как ${\begin{aligned}\mathbf {v} (t)&=\mathbf {r} '(t)\\&=(x'(t),y'(t),z'(t))\,,\end{aligned}}$

и его ускорение как ${\begin{aligned}\mathbf {a} (t)&=\mathbf {v} '(t)=\mathbf {r} ''(t)\\&=(x''(t),y''(t),z''(t))\,.\end{aligned}}$

Компьютерное проектирование

Еще одно важное применение параметрических уравнений - в области автоматизированного проектирования (САПР). ^[7] Например, рассмотрим следующие три представления, каждое из которых обычно используется для описания плоских кривых .

Тип	Форма	Пример	Описание
Явный	$y=f(x)\,\!$	$y=mx+b\,\!$	Линия
Скрытый	$f(x,y)=0\,\!$	$\left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}$	Круг
Параметрический	$x={\frac {g(t)}{w(t)}};\,\!$ $y={\frac {h(t)}{w(t)}}$	$x=a_{0}+a_{1}t;\,\!$ $y=b_{0}+b_{1}t\,\!$	Линия
Параметрический	$x={\frac {g(t)}{w(t)}};\,\!$ $y={\frac {h(t)}{w(t)}}$	$x=a+r\,\cos t;\,\!$ $y=b+r\,\sin t\,\!$	Круг

Каждое представление имеет преимущества и недостатки для приложений САПР.

Явное представление может быть очень сложным или даже отсутствовать. Более того, он плохо себя ведет при геометрических преобразованиях , и в частности при поворотах . С другой стороны, поскольку параметрическое уравнение и неявное уравнение можно легко вывести из явного представления, когда простое явное представление существует, оно имеет преимущества обоих других представлений.

Неявные представления могут затруднить создание точек на кривой и даже принятие решения о том, существуют ли реальные точки. С другой стороны, они хорошо подходят для определения того, находится ли данная точка на кривой или находится внутри или снаружи замкнутой кривой.

Такие решения могут быть трудными при использовании параметрического представления, но параметрические представления лучше всего подходят для создания точек на кривой и ее построения. ^[8]

Целочисленная геометрия

Многие задачи целочисленной геометрии можно решить с помощью параметрических уравнений. Классическим таким решением является прямоугольных параметризация Евклидом треугольников , у которых длины их сторон $a, b$ и их гипотенузы $c$ являются взаимно простыми целыми числами . Поскольку $a$ и $b$ не являются четными (иначе $a, b$ и $c$ не были бы взаимно простыми), их можно поменять местами, чтобы получить $четное$ , и тогда параметризация будет

${\begin{aligned}a&=2mn\\b&=m^{2}-n^{2}\\c&=m^{2}+n^{2}\,,\end{aligned}}$

где параметры $m$ и $n$ — положительные взаимно простые целые числа, которые не являются нечетными.

Умножив $a, b$ и $c$ на произвольное положительное целое число, можно получить параметризацию всех прямоугольных треугольников, три стороны которых имеют целые длины.

Имплицитизация

Преобразование набора параметрических уравнений в одно неявное уравнение включает исключение переменной $t$ из одновременных уравнений. $x=f(t),\ y=g(t).$ Этот процесс называется имплицитизацией . Если одно из этих уравнений можно решить относительно $t$ , полученное выражение можно подставить в другое уравнение, чтобы получить уравнение, включающее $только x$ и $y$ : $y=g(t)$ чтобы получить $t=g^{-1}(y)$ и используя это в $x=f(t)$ дает явное уравнение $x=f(g^{-1}(y)),$ в то время как более сложные случаи дадут неявное уравнение вида $h(x,y)=0.$

Если параметризация задается рациональными функциями $x={\frac {p(t)}{r(t)}},\qquad y={\frac {q(t)}{r(t)}},$

где $p$ , $q$ и $r$ являются взаимно простыми полиномами, результирующее вычисление позволяет делать неявные вычисления. Точнее, неявное уравнение является результирующим относительно $t$ уравнений $xr (t) - p (t)$ и $yr (t) - q (t)$ .

В более высоких измерениях (более двух координат или более одного параметра) имплицитизация рациональных параметрических уравнений может быть выполнена с помощью на основе базиса Грёбнера вычислений ; см. базис Грёбнера § Имплицитизация в более высоком измерении .

На примере круга радиуса $a$ параметрические уравнения ${\begin{aligned}x&=a\cos(t)\\y&=a\sin(t)\end{aligned}}$

может быть неявно выражено в терминах $x$ и $y$ посредством тригонометрического тождества Пифагора . С

${\begin{aligned}{\frac {x}{a}}&=\cos(t)\\{\frac {y}{a}}&=\sin(t)\\\end{aligned}}$ и $\cos(t)^{2}+\sin(t)^{2}=1,$ мы получаем $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{a}}\right)^{2}=1,$ и таким образом $x^{2}+y^{2}=a^{2},$

что является стандартным уравнением окружности с центром в начале координат.

Примеры в двух измерениях

Парабола

Простейшее уравнение параболы . $y=x^{2}$

может быть (тривиально) параметризовано с помощью свободного параметра $t$ и установки $x=t,y=t^{2}\quad \mathrm {for} -\infty <t<\infty .$

Явные уравнения

В более общем смысле, любая кривая, заданная явным уравнением $y=f(x)$

может быть (тривиально) параметризовано с помощью свободного параметра $t$ и установки $x=t,y=f(t)\quad \mathrm {for} -\infty <t<\infty .$

Круг

Более сложный пример заключается в следующем. Рассмотрим единичную окружность, описываемую обыкновенным (декартовым) уравнением $x^{2}+y^{2}=1.$

Это уравнение можно параметризовать следующим образом: $(x,y)=(\cos(t),\;\sin(t))\quad \mathrm {for} \ 0\leq t<2\pi .$

С помощью декартова уравнения легче проверить, лежит ли точка на окружности или нет. В параметрической версии легче получать точки на графике.

В некоторых контекстах предпочтительными являются параметрические уравнения, включающие только рациональные функции (то есть дроби двух многочленов ), если они существуют. В случае круга такая рациональная параметризация имеет вид ${\begin{aligned}x&={\frac {1-t^{2}}{1+t^{2}}}\\y&={\frac {2t}{1+t^{2}}}\,.\end{aligned}}$

С помощью этой пары параметрических уравнений точка $(-1, 0)$ представлена не действительным значением $t$ , а пределом x и $когда$ y $,$ t $стремится$ к бесконечности .

Эллипс

Эллипс в каноническом положении (центр в начале координат, большая ось вдоль $оси x$ ) с полуосями $a$ и $b$ можно параметрически представить как ${\begin{aligned}x&=a\,\cos t\\y&=b\,\sin t\,.\end{aligned}}$

Эллипс в общем положении можно выразить как ${\begin{alignedat}{4}x={}&&X_{\mathrm {c} }&+a\,\cos t\,\cos \varphi {}&&-b\,\sin t\,\sin \varphi \\y={}&&Y_{\mathrm {c} }&+a\,\cos t\,\sin \varphi {}&&+b\,\sin t\,\cos \varphi \end{alignedat}}$

поскольку параметр $t$ изменяется от $0$ до $2 π$ . Здесь $(X c, Y c)$ — центр эллипса, а $φ$ — угол между $осью x$ и большой осью эллипса.

Обе параметризации можно сделать рациональными , используя формулу касательного полуугла и установив ${\textstyle \tan {\frac {t}{2}}=u\,.}$

Кривая Лиссажу

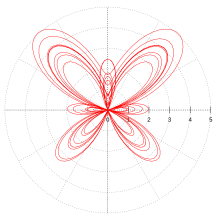
Кривая Лиссажу похожа на эллипс, но $x$ и $y$ синусоиды не находятся в фазе. В каноническом положении кривая Лиссажу имеет вид ${\begin{aligned}x&=a\,\cos(k_{x}t)\\y&=b\,\sin(k_{y}t)\end{aligned}}$ где $k x$ и $k y$ — константы, описывающие количество лепестков фигуры.

Гипербола

открытия с востока на запад Гиперболу можно параметрически представить как

${\begin{aligned}x&=a\sec t+h\\y&=b\tan t+k\,,\end{aligned}}$

или, рационально

${\begin{aligned}x&=a{\frac {1+t^{2}}{1-t^{2}}}+h\\y&=b{\frac {2t}{1-t^{2}}}+k\,.\end{aligned}}$

Гиперболу открытия с севера на юг можно параметрически представить как

${\begin{aligned}x&=b\tan t+h\\y&=a\sec t+k\,,\end{aligned}}$

или, рационально

${\begin{aligned}x&=b{\frac {2t}{1-t^{2}}}+h\\y&=a{\frac {1+t^{2}}{1-t^{2}}}+k\,.\end{aligned}}$

Во всех этих формулах $(h, k)$ — координаты центра гиперболы, $a$ — длина большой полуоси, а $b$ — длина малой полуоси. Обратите внимание, что в рациональных формах этих формул точки $(-a, 0)$ и $(0, -a)$ соответственно не представлены действительным значением $t$ , но являются пределом $x$ и $y$ , поскольку $t$ стремится к бесконечность.

Гипотрохоид

Гипотрохоида — это кривая , очерченная точкой, прикрепленной к окружности радиуса $r,$ катящейся вокруг внутренней части фиксированной окружности радиуса $R$ , где точка находится на расстоянии $d$ от центра внутренней окружности.

Гипотрохоид, для которого $r = d$
Гипотрохоид, для которого $R = 5$ , $r = 3$ , $d = 5.$

Параметрические уравнения для гипотрохоидов:

${\begin{aligned}x(\theta )&=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\y(\theta )&=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\,.\end{aligned}}$

Некоторые примеры:

$р = 6$ $р = 4$ $д = 1$
$р = 7$ $р = 4$ $д = 1$
$R = 8$ $r = 3$ $d = 2$
$р = 7$ $р = 4$ $д = 2$
$р = 15$ $р = 14$ $д = 1$

Примеры в трех измерениях

Анимированная параметрическая спираль

спираль

Параметрические уравнения удобны для описания кривых в пространствах более высокой размерности. Например:

${\begin{aligned}x&=a\cos(t)\\y&=a\sin(t)\\z&=bt\,\end{aligned}}$

описывает трехмерную кривую, спираль с радиусом $a$ и поднимающуюся на $2 π b$ единиц за оборот. Уравнения на плоскости идентичны уравнениям для окружности.Такие выражения, как приведенное выше, обычно записываются как

${\begin{aligned}\mathbf {r} (t)&=(x(t),y(t),z(t))\\&=(a\cos(t),a\sin(t),bt)\,,\end{aligned}}$

где $r$ — трехмерный вектор.

Параметрические поверхности

Тор r с большим радиусом $R$ и малым радиусом $можно$ параметрически определить как

${\begin{aligned}x&=\cos(t)\left(R+r\cos(u)\right),\\y&=\sin(t)\left(R+r\cos(u)\right),\\z&=r\sin(u)\,.\end{aligned}}$

где два параметра $t$ и $u$ варьируются от $0$ до $2 π$ .

$р = 2$ , $р = 1/2$

При $u$ от $0$ до $2π изменении$ точка на поверхности движется по короткой окружности, проходящей через отверстие в торе. При $t$ изменении $от 0$ до $2 π$ точка на поверхности движется по длинному кругу вокруг отверстия в торе.

Пример с векторами

Параметрическое уравнение прямой, проходящей через точку $\left(x_{0},y_{0},z_{0}\right)$ и параллельно вектору $a{\hat {\mathbf {i} }}+b{\hat {\mathbf {j} }}+c{\hat {\mathbf {k} }}$ является ^[9]

${\begin{aligned}x&=x_{0}+at\\y&=y_{0}+bt\\z&=z_{0}+ct\end{aligned}}$

Недоопределенные линейные системы

Система m $если$ линейных уравнений с $n$ неизвестными называется недоопределенной, она имеет более одного решения. Это происходит, когда матрица системы и ее дополненная матрица имеют одинаковый ранг $r$ и $r < n$ . В этом случае можно выбрать $n - r$ неизвестных в качестве параметров и представить все решения в виде параметрического уравнения, где все неизвестные выражаются как линейные комбинации выбранных. То есть, если неизвестные $x_{1},\ldots ,x_{n},$ их можно переупорядочить, чтобы выразить решения как ^[10]

${\begin{aligned}x_{1}&=\beta _{1}+\sum _{j=r+1}^{n}\alpha _{1,j}x_{j}\\\vdots \\x_{r}&=\beta _{r}+\sum _{j=r+1}^{n}\alpha _{r,j}x_{j}\\x_{r+1}&=x_{r+1}\\\vdots \\x_{n}&=x_{n}.\end{aligned}}$

Такое параметрическое уравнение называется параметрической формой решения системы. ^[10]

Стандартный метод вычисления параметрической формы решения заключается в использовании метода исключения Гаусса для вычисления уменьшенной ступенчатой формы расширенной матрицы. Тогда неизвестные, которые можно использовать в качестве параметров, — это те, которые соответствуют столбцам, не содержащим какой-либо ведущей записи (то есть крайней левой ненулевой записи в строке или матрице), и параметрическую форму можно вывести напрямую. ^[10]

См. также

Примечания

↑ Перейти обратно: Перейти обратно: ^а ^б ^с Вайсштейн, Эрик В. «Параметрические уравнения» . Математический мир .
^ Крейциг, Эрвин (1972). Высшая инженерная математика (3-е изд.). Нью-Йорк: Уайли . стр. 291, 342. ISBN. 0-471-50728-8 .
^ Берден, Ричард Л.; Фейрес, Дж. Дуглас (1993). Численный анализ (5-е изд.). Бостон: Брукс/Коул . п. 149. ИСБН 0-534-93219-3 .
^ Томас, Джордж Б.; Финни, Росс Л. (1979). Исчисление и аналитическая геометрия (пятое изд.). Аддисон-Уэсли . п. 91.
^ Никамп, Дуэйн. «Пример параметризации плоскости» . mathinsight.org . Проверено 14 апреля 2017 г.
^ Шпицбарт, Авраам (1975). Исчисление с аналитической геометрией . Глевью, Иллинойс: Скотт, Форесман и компания. ISBN 0-673-07907-4 . Проверено 30 августа 2015 г.
^ Стюарт, Джеймс (2003). Исчисление (5-е изд.). Бельмонт, Калифорния: Thomson Learning, Inc., стр. 687–689 . ISBN 0-534-39339-Х .
^ Шах, Джами Дж .; Мартти Мантила (1995). Параметрическое и функциональное CAD/CAM: концепции, методы и приложения . Нью-Йорк, штат Нью-Йорк: John Wiley & Sons, Inc., стр. 29–31. ISBN 0-471-00214-3 .
^ Исчисление: одно- и многомерное . Джон Уайли. 2012-10-29. п. 919. ИСБН 9780470888612 . OCLC 828768012 .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Антон, Ховард; Роррес, Крис (2014) [1973]. «1.2 Исключение по Гауссу» . Элементарная линейная алгебра (11-е изд.). Уайли. стр. 11–24.

Внешние ссылки

[MathWorld-1] Перейти обратно: Перейти обратно: ^а ^б ^с Вайсштейн, Эрик В. «Параметрические уравнения» . Математический мир .

[2] Крейциг, Эрвин (1972). Высшая инженерная математика (3-е изд.). Нью-Йорк: Уайли . стр. 291, 342. ISBN. 0-471-50728-8 .

[3] Берден, Ричард Л.; Фейрес, Дж. Дуглас (1993). Численный анализ (5-е изд.). Бостон: Брукс/Коул . п. 149. ИСБН 0-534-93219-3 .

[4] Томас, Джордж Б.; Финни, Росс Л. (1979). Исчисление и аналитическая геометрия (пятое изд.). Аддисон-Уэсли . п. 91.

[5] Никамп, Дуэйн. «Пример параметризации плоскости» . mathinsight.org . Проверено 14 апреля 2017 г.

[6] Шпицбарт, Авраам (1975). Исчисление с аналитической геометрией . Глевью, Иллинойс: Скотт, Форесман и компания. ISBN 0-673-07907-4 . Проверено 30 августа 2015 г.

[7] Стюарт, Джеймс (2003). Исчисление (5-е изд.). Бельмонт, Калифорния: Thomson Learning, Inc., стр. 687–689 . ISBN 0-534-39339-Х .

[8] Шах, Джами Дж .; Мартти Мантила (1995). Параметрическое и функциональное CAD/CAM: концепции, методы и приложения . Нью-Йорк, штат Нью-Йорк: John Wiley & Sons, Inc., стр. 29–31. ISBN 0-471-00214-3 .

[9] Исчисление: одно- и многомерное . Джон Уайли. 2012-10-29. п. 919. ИСБН 9780470888612 . OCLC 828768012 .

[anton-10] Перейти обратно: Перейти обратно: ^а ^б ^с Антон, Ховард; Роррес, Крис (2014) [1973]. «1.2 Исключение по Гауссу» . Элементарная линейная алгебра (11-е изд.). Уайли. стр. 11–24.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]