Конциклические точки

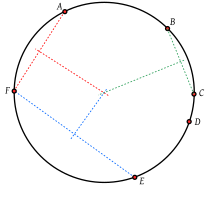
Совпадающие серединные перпендикуляры хорд между солежащими точками

В геометрии множество ) , точек если они называется конциклическими (или коциклическими лежат на одной окружности . Многоугольник , которого вершины лежат на одной окружности, называется циклическим многоугольником , а окружность — описанной вокруг него окружностью или описанной окружностью . Все конциклические точки равноудалены от центра круга.

Три точки плоскости , которые не все попадают на прямую линию, лежат на одной окружности, поэтому каждый треугольник представляет собой циклический многоугольник с четко определенной описанной окружностью . Однако четыре или более точки плоскости не обязательно лежат на одной окружности. частный случай вписанных четырехугольников После треугольников наиболее подробно изучен .

Перпендикулярные биссектрисы

В общем случае центр O круга, на котором лежат точки P и Q, должен быть таким, чтобы OP и OQ были равными расстояниями. Следовательно, O должен лежать на серединном перпендикуляре отрезка PQ . ^[1] Для n различных точек существует n ( n - 1)/2 биссектрисы, и условие концикличности состоит в том, что все они встречаются в одной точке, центре O .

Треугольники

Вершины каждого треугольника лежат на окружности, называемой описанной окружностью . (Из-за этого некоторые авторы определяют термин «конциклический» только в контексте четырех и более точек на окружности.) ^[2] Несколько других наборов точек, определенных треугольником, также являются конциклическими и имеют разные окружности; см. девятиконечный круг ^[3] и теорема Лестера . ^[4]

Радиус . окружности, на которой лежит набор точек, по определению является радиусом описанной окружности любого треугольника с вершинами в любых трех из этих точек Если попарные расстояния между тремя точками равны a , b и c , то радиус круга равен

R={\sqrt {\frac {a^{2}b^{2}c^{2}}{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}.

приведены уравнение описанной окружности треугольника, а также выражения для радиуса и координат центра окружности через декартовы координаты вершин Здесь .

Другие конциклические точки

В любом треугольнике все следующие девять точек лежат на одной окружности с так называемым кругом девяти точек : середины трех ребер, основания трех высот и точки на полпути между ортоцентром и каждой из трех вершин.

Теорема Лестера утверждает, что в любом разностороннем треугольнике две точки Ферма , девятиточечный центр и описанный центр лежат на одной окружности.

Если линии провести через точку Лемуана , параллельные сторонам треугольника, то шесть точек пересечения линий и сторон треугольника лежат на одной окружности, в так называемом круге Лемуана .

Круг Ван Ламоена, связанный с любым данным треугольником. $T$ содержит центры описанных шести треугольников, которые определены внутри $T$ по трем медианам .

треугольника Центр описанной окружности , его точка Лемуана и первые две точки Брокара лежат на одной окружности, при этом отрезок от центра описанной окружности до точки Лемуана является диаметром . ^[5]

Циклические четырехугольники

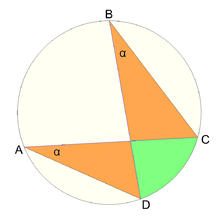
Четырехугольник ABCD с вершинами, лежащими на одной окружности, называется вписанным четырехугольником ; это произойдет тогда и только тогда, когда $\angle CAD=\angle CBD$ ( теорема о вписанном угле ), которая верна тогда и только тогда, когда противоположные углы внутри четырехугольника являются дополнительными . ^[6] Вписанный четырехугольник с последовательными сторонами a , b , c , d и полупериметром s = ( a + b + c + d )/2 имеет радиус описанной окружности, заданный выражением ^[7]^[8]

R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}},

выражение, выведенное индийским математиком Ватасери Парамешварой в 15 веке.

По теореме Птолемея , если четырехугольник задан попарными расстояниями между его четырьмя вершинами A , B , C и D по порядку, то он циклический тогда и только тогда, когда произведение диагоналей равно сумме произведений противоположных сторон. :

AC\cdot BD=AB\cdot CD+BC\cdot AD.

Если две прямые, одна из которых содержит отрезок AC , а другая — отрезок BD , пересекаются в точке X , то четыре точки A , B , C , D лежат на одной окружности тогда и только тогда, когда ^[9]

\displaystyle AX\cdot XC=BX\cdot XD.

Пересечение X может быть внутренним или внешним по отношению к кругу. Эта теорема известна как степень точки .

Выпуклый четырехугольник является ортодиагональным (имеет перпендикулярные диагонали) тогда и только тогда, когда середины сторон и основания четырех высот представляют собой восемь конциклических точек, на так называемом восьмиточечном круге .

Циклические полигоны

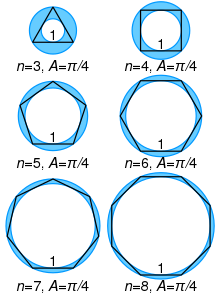
В более общем смысле многоугольник , в котором все вершины лежат на одной окружности, называется циклическим многоугольником . Многоугольник является циклическим тогда и только тогда, когда серединные перпендикуляры его ребер совпадают . ^[10] Каждый правильный многоугольник является циклическим многоугольником.

У вписанного многоугольника с нечетным числом сторон все углы равны тогда и только тогда, когда многоугольник правильный. Вписанный многоугольник с четным числом сторон имеет все углы равными тогда и только тогда, когда равны чередующиеся стороны (т. е. равны стороны 1, 3, 5, … , а также стороны 2, 4, 6, … ). ^[11]

Вписанный пятиугольник с рациональными сторонами и площадью известен как пятиугольник Роббинса . Во всех известных случаях его диагонали также имеют рациональную длину, хотя верно ли это для всех возможных пятиугольников Роббинса — нерешенная проблема. ^[12]

В любом циклическом $n$ -угольнике с четным $n$ сумма одного набора альтернативных углов (первого, третьего, пятого и т. д.) равна сумме другого набора альтернативных углов. Это можно доказать индукцией из $случая n = 4$ , заменяя в каждом случае сторону еще тремя сторонами и отмечая, что эти три новые стороны вместе со старой стороной образуют четырехугольник, который сам обладает этим свойством; чередующиеся углы последнего четырехугольника представляют собой дополнения к суммам чередующихся углов предыдущего $n$ -угольника.

Тангенциальный многоугольник — это многоугольник, в который вписанная окружность касается каждой стороны многоугольника; таким образом, эти точки касания соприкасаются с вписанной окружностью. Пусть один $n$ -угольник вписан в окружность, а другой $n$ -угольник касается этой окружности в вершинах первого $n$ -угольника. Тогда из любой точки $P$ на окружности произведение расстояний по перпендикуляру от $P$ до сторон первого $n$ -угольника равно произведению расстояний по перпендикуляру от $P$ до сторон второго $n$ -угольника. ^[13]

Точка на описанной окружности

Пусть циклический $n$ -угольник имеет вершины $A 1, \dots, An на$ единичной окружности. Тогда для любой точки $M$ на малой дуге $A 1 An условию$ расстояния от $M$ до вершин удовлетворяют ^[14]

{\begin{cases}{\overline {MA_{1}}}+{\overline {MA_{3}}}+\cdots +{\overline {MA_{n-2}}}+{\overline {MA_{n}}}<n/{\sqrt {2}}&{\text{if }}n{\text{ is odd}};\\{\overline {MA_{1}}}+{\overline {MA_{3}}}+\cdots +{\overline {MA_{n-3}}}+{\overline {MA_{n-1}}}\leq n/{\sqrt {2}}&{\text{if }}n{\text{ is even}}.\end{cases}}

Для правильного $n$ -угольника, если ${\overline {MA_{i}}}$ — расстояния от любой точки $M$ на описанной окружности до вершин $A i$ , тогда ^[15]

3({\overline {MA_{1}}}^{2}+{\overline {MA_{2}}}^{2}+\dots +{\overline {MA_{n}}}^{2})^{2}=2n({\overline {MA_{1}}}^{4}+{\overline {MA_{2}}}^{4}+\dots +{\overline {MA_{n}}}^{4}).

Константа описания многоугольника

Любой правильный многоугольник является циклическим. Рассмотрим единичную окружность, затем описали правильный треугольник так, чтобы каждая сторона касалась окружности. Опишите круг, затем описанный квадрат. Снова описали окружность, затем описали правильный пятиугольник и так далее. Радиусы описанных окружностей сходятся к так называемой константе описания многоугольника.

\prod _{n=3}^{\infty }{\frac {1}{\cos \left({\frac {\pi }{n}}\right)}}=8.7000366\ldots .

(последовательность A051762 в OEIS ). Обратной величиной этой константы является константа Кеплера-Бувкампа .

Вариации

В контекстах, где линии рассматриваются как тип обобщенного круга с бесконечным радиусом, коллинеарные точки (точки вдоль одной линии) считаются конциклическими. Эта точка зрения полезна, например, при изучении инверсии окружности или, в более общем смысле, преобразований Мёбиуса (геометрических преобразований, порождаемых отражениями и инверсиями окружностей), поскольку эти преобразования сохраняют концикличность точек только в этом расширенном смысле. ^[16]

В комплексной плоскости (сформированной путем рассмотрения вещественной и мнимой частей комплексного числа как плоскости x и y декартовых координат ) концикличность имеет особенно простую формулировку: четыре точки на комплексной плоскости либо концикличны, либо коллинеарны тогда и только тогда. если их перекрестное отношение является действительным числом . ^[17]

Целочисленная площадь и длины сторон

Некоторые циклические многоугольники обладают тем свойством, что их площадь и все длины сторон являются положительными целыми числами. Треугольники, обладающие этим свойством, называются героновыми треугольниками ; циклические четырехугольники, обладающие этим свойством (и тем, что диагонали, соединяющие противоположные вершины, имеют целую длину), называются четырехугольниками Брахмагупты ; циклические пятиугольники, обладающие этим свойством, называются пятиугольниками Роббинса . В более общем смысле, версии этих циклических многоугольников, масштабированные по рациональному числу, будут иметь площадь и длину сторон, которые являются рациональными числами.

Пусть $θ 1$ будет углом, охватываемым одной стороной вписанного многоугольника, если смотреть из центра описанной окружности. Аналогично определим центральные углы $θ 2, ..., θ n$ для остальных $n - 1$ сторон. Каждый геронов треугольник и каждый четырехугольник Брахмагупты имеют рациональное значение тангенса четверти угла $tan θ k /4$ для каждого значения $k$ . Каждый известный пятиугольник Роббинса (имеет диагонали рациональной длины) обладает этим свойством, хотя нерешенной является проблема, обладает ли каждый возможный пятиугольник Роббинса этим свойством.

Обратное верно для всех циклических многоугольников с любым количеством сторон; если все такие центральные углы имеют рациональные касательные к своим четвертям углов, то подразумеваемый циклический многоугольник, описанный единичной окружностью, будет одновременно иметь рациональные длины сторон и рациональную площадь. Кроме того, каждая диагональ, соединяющая две вершины, независимо от того, являются ли эти две вершины смежными, будет иметь рациональную длину. Такой циклический многоугольник можно масштабировать так, чтобы его площадь и длина были целыми числами.

Это обратное соотношение дает возможность создавать циклические многоугольники с целочисленной площадью, сторонами и диагоналями. Для многоугольника с $n$ сторонами пусть $0 < c 1 < ... < c n -1 < +\infty$ — рациональные числа. Это тангенсы одной четверти совокупных углов $θ 1$ , $θ 1 + θ 2$ , ..., $θ 1 + ... + θ n -1$ . Пусть $q 1 = c 1$ , пусть $q n = 1 / c n -1$ , и пусть $q k = (c k - c k -1) / (1 + c k c k -1)$ для $k = 2, .. ., п -1$ . Эти рациональные числа представляют собой тангенсы отдельных четвертей углов, используя формулу тангенса разности углов. Рациональные длины сторон многоугольника, описанного единичной окружностью, таким образом, получаются как $s k = 4 q k / (1 + q k 2)$ . Рациональная площадь равна $A = \sum k 2 q k (1 - q k 2) / (1 + q k 2) 2$ . Их можно преобразовать в целые числа, масштабируя длины сторон с помощью общей константы.

Другие объекты недвижимости

Набор из пяти или более точек является конциклическим тогда и только тогда, когда каждое подмножество из четырех точек конциклично. ^[18] Это свойство можно рассматривать как аналог концикличности свойства Хелли выпуклых множеств.

Минимальный ограничивающий круг

С этим связано понятие минимального ограничивающего круга , который представляет собой наименьший круг, полностью содержащий набор точек. Каждый набор точек на плоскости имеет уникальный минимальный ограничивающий круг, который может быть построен с помощью алгоритма линейного времени . ^[19]

Даже если набор точек конциклен, их описанная окружность может отличаться от минимальной ограничивающей окружности. Например, для тупоугольного треугольника минимальный ограничивающий круг имеет диаметр самой длинной стороны и не проходит через противоположную вершину.

Ссылки

^ Либескинд, Шломо (2008), Евклидова и трансформационная геометрия: дедуктивное исследование , Jones & Bartlett Learning, с. 21, ISBN 9780763743666 /
^ Эллиотт, Джон (1902), «Элементарная геометрия» , Swan Sonnenschein & co., стр. 126 .
^ Айзекс, И. Мартин (2009), Геометрия для студентов колледжей , Чистые и прикладные тексты для студентов, том. 8, Американское математическое общество, с. 63, ISBN 9780821847947 .
^ Ю, Пол (2010), «Круги Лестера, Эванса, Парри и их обобщения» (PDF) , Forum Geometricorum , 10 : 175–209, MR 2868943 .
^ Скотт, Дж. А. «Некоторые примеры использования площадных координат в геометрии треугольника», Mathematical Gazette 83, ноябрь 1999 г., 472–477.
^ Педо, Дэн (1997), Круги: математический взгляд , Спектр MAA (2-е изд.), Cambridge University Press, стр. XXII, ISBN 9780883855188 .
^ Альсина, Клауди; Нельсен, Роджер Б. (2007), «О диагоналях вписанного четырехугольника» (PDF) , Forum Geometricorum , 7 : 147–9
^ Хен, Ларри (март 2000 г.), «Описанный радиус вписанного четырехугольника», Mathematical Gazette , 84 (499): 69–70, doi : 10.2307/3621477 , JSTOR 3621477
^ Брэдли, Кристофер Дж. (2007), Алгебра геометрии: декартова, площадная и проективная координаты , Highperception, с. 179, ISBN 978-1906338008 , OCLC 213434422
^ Байер, Оуэн; Лазебник, Феликс; Смелцер, Дейдра Л. (2010), Методы евклидовой геометрии , Математическая ассоциация Америки, стр. 77, ISBN 9780883857632 .
^ Де Вильерс, Майкл (март 2011 г.). «95.14 Равноугольные циклические и равносторонние описанные многоугольники». Математический вестник . 95 (532): 102–107. дои : 10.1017/S0025557200002461 . JSTOR 23248632 . S2CID 233361080 .
^ Бухгольц, Ральф Х.; МакДугалл, Джеймс А. (2008). «Циклические многоугольники с рациональными сторонами и площадью» . Журнал теории чисел . 128 (1): 17–48. дои : 10.1016/j.jnt.2007.05.005 . МР 2382768 .
^ Джонсон, Роджер А. (1929). Современная геометрия: элементарный трактат о геометрии треугольника и круга . Houghton Mifflin Co. p. 72. hdl : 2027/wu.89043163211 . Переиздано Dover Publications под названием Advanced Euclidean Geometry , 1960 и 2007 гг.
^ «Неравенства, предложенные в Crux Mathematicum » (PDF) . ИМО Сборник п. 190, №332.10.
^ Месхишвили, Мамука (2020). «Циклические средние правильных многоугольников и платоновых тел» . Коммуникации в математике и приложениях . 11 : 335–355. arXiv : 2010.12340 . doi : 10.26713/cma.v11i3.1420 (неактивен 31 января 2024 г.). {{cite journal}}: CS1 maint: DOI неактивен по состоянию на январь 2024 г. ( ссылка )
^ Цвиккер, К. (2005), Расширенная геометрия плоских кривых и их применение , Courier Dover Publications, стр. 24, ISBN 9780486442761 .
^ Хан, Лян-шин (1996), Комплексные числа и геометрия , Спектр MAA (2-е изд.), Издательство Кембриджского университета, стр. 65, ISBN 9780883855102 .
^ Педо, Дэн (1988), Геометрия: всесторонний курс , Courier Dover Publications, стр. 431, ISBN 9780486658124 .
^ Мегиддо, Н. (1983). «Алгоритмы линейного времени для линейного программирования в R ³ и связанные с ними проблемы». SIAM Journal on Computing . 12 (4): 759–776. doi : 10.1137/0212052 . S2CID 14467740 .

Внешние ссылки

Вайсштейн, Эрик В. «Конциклический» . Математический мир .
Четыре конциклические точки Михаэля Шрайбера, Демонстрационный проект Вольфрама .

[1] Либескинд, Шломо (2008), Евклидова и трансформационная геометрия: дедуктивное исследование , Jones & Bartlett Learning, с. 21, ISBN 9780763743666 /

[2] Эллиотт, Джон (1902), «Элементарная геометрия» , Swan Sonnenschein & co., стр. 126 .

[3] Айзекс, И. Мартин (2009), Геометрия для студентов колледжей , Чистые и прикладные тексты для студентов, том. 8, Американское математическое общество, с. 63, ISBN 9780821847947 .

[4] Ю, Пол (2010), «Круги Лестера, Эванса, Парри и их обобщения» (PDF) , Forum Geometricorum , 10 : 175–209, MR 2868943 .

[5] Скотт, Дж. А. «Некоторые примеры использования площадных координат в геометрии треугольника», Mathematical Gazette 83, ноябрь 1999 г., 472–477.

[6] Педо, Дэн (1997), Круги: математический взгляд , Спектр MAA (2-е изд.), Cambridge University Press, стр. XXII, ISBN 9780883855188 .

[Alsina2-7] Альсина, Клауди; Нельсен, Роджер Б. (2007), «О диагоналях вписанного четырехугольника» (PDF) , Forum Geometricorum , 7 : 147–9

[8] Хен, Ларри (март 2000 г.), «Описанный радиус вписанного четырехугольника», Mathematical Gazette , 84 (499): 69–70, doi : 10.2307/3621477 , JSTOR 3621477

[9] Брэдли, Кристофер Дж. (2007), Алгебра геометрии: декартова, площадная и проективная координаты , Highperception, с. 179, ISBN 978-1906338008 , OCLC 213434422

[10] Байер, Оуэн; Лазебник, Феликс; Смелцер, Дейдра Л. (2010), Методы евклидовой геометрии , Математическая ассоциация Америки, стр. 77, ISBN 9780883857632 .

[11] Де Вильерс, Майкл (март 2011 г.). «95.14 Равноугольные циклические и равносторонние описанные многоугольники». Математический вестник . 95 (532): 102–107. дои : 10.1017/S0025557200002461 . JSTOR 23248632 . S2CID 233361080 .

[12] Бухгольц, Ральф Х.; МакДугалл, Джеймс А. (2008). «Циклические многоугольники с рациональными сторонами и площадью» . Журнал теории чисел . 128 (1): 17–48. дои : 10.1016/j.jnt.2007.05.005 . МР 2382768 .

[13] Джонсон, Роджер А. (1929). Современная геометрия: элементарный трактат о геометрии треугольника и круга . Houghton Mifflin Co. p. 72. hdl : 2027/wu.89043163211 . Переиздано Dover Publications под названием Advanced Euclidean Geometry , 1960 и 2007 гг.

[14] «Неравенства, предложенные в Crux Mathematicum » (PDF) . ИМО Сборник п. 190, №332.10.

[Mamuka-15] Месхишвили, Мамука (2020). «Циклические средние правильных многоугольников и платоновых тел» . Коммуникации в математике и приложениях . 11 : 335–355. arXiv : 2010.12340 . doi : 10.26713/cma.v11i3.1420 (неактивен 31 января 2024 г.). {{cite journal}}: CS1 maint: DOI неактивен по состоянию на январь 2024 г. ( ссылка )

[16] Цвиккер, К. (2005), Расширенная геометрия плоских кривых и их применение , Courier Dover Publications, стр. 24, ISBN 9780486442761 .

[17] Хан, Лян-шин (1996), Комплексные числа и геометрия , Спектр MAA (2-е изд.), Издательство Кембриджского университета, стр. 65, ISBN 9780883855102 .

[18] Педо, Дэн (1988), Геометрия: всесторонний курс , Courier Dover Publications, стр. 431, ISBN 9780486658124 .

[19] Мегиддо, Н. (1983). «Алгоритмы линейного времени для линейного программирования в R ³ и связанные с ними проблемы». SIAM Journal on Computing . 12 (4): 759–776. doi : 10.1137/0212052 . S2CID 14467740 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]