Цилиндрическая система координат

Цилиндрическая система координат — это трехмерная система координат , которая определяет положения точек по расстоянию от выбранной базовой оси (ось L на изображении напротив) , направлению от оси относительно выбранного исходного направления (ось A) и расстояние от выбранной базовой плоскости, перпендикулярной оси (плоскость, содержащая фиолетовую секцию) . Последнее расстояние задается как положительное или отрицательное число в зависимости от того, какая сторона базовой плоскости обращена к точке.

Началом . системы является точка, в которой все три координаты могут быть заданы как ноль Это пересечение базовой плоскости и оси.Ось по-разному называют цилиндрической или продольной осью, чтобы отличить ее от полярной оси , которая представляет собой луч , лежащий в базовой плоскости, начинающийся в начале координат и указывающий в исходном направлении.Другие направления, перпендикулярные продольной оси, называются радиальными линиями .

Расстояние от оси можно назвать радиальным расстоянием или радиусом , а угловую координату иногда называют угловым положением или азимутом . Радиус и азимут вместе называются полярными координатами , поскольку они соответствуют двумерной полярной системе координат в плоскости, проходящей через точку, параллельную базовой плоскости. Третьей координатой можно назвать высоту или высоту (если плоскость отсчета считать горизонтальной), продольное положение , ^[1] или осевое положение . ^[2]

Цилиндрические координаты полезны в связи с объектами и явлениями, имеющими некоторую вращательную симметрию относительно продольной оси, например, поток воды в прямой трубе круглого сечения, распределение тепла в металлическом цилиндре , электромагнитные поля, создаваемые электрическим током в длинный прямой провод, аккреционные диски в астрономии и так далее.

Их иногда называют «цилиндрическими полярными координатами». ^[3] и «полярные цилиндрические координаты», ^[4] и иногда используются для указания положения звезд в галактике («галактоцентрические цилиндрические полярные координаты»). ^[5]

Определение

Три координаты ( $ρ$ , $φ$ , $z$ ) точки $P$ определяются как:

Радиальное расстояние $ρ$ это евклидово расстояние от $оси z$ до точки $P.$ —
Азимут — это $φ$ угол между опорным направлением на выбранной плоскости и линией от начала координат до проекции $P$ на плоскость.
Осевая координата или высота $z$ знаком от выбранной плоскости до точки $P.$ — это расстояние со

Уникальные цилиндрические координаты

Как и в полярных координатах, одна и та же точка с цилиндрическими координатами $(ρ, φ, z)$ имеет бесконечно много эквивалентных координат, а именно $(ρ, φ \pm n \times360°, z)$ и $(- ρ, φ \pm (2 n + 1) \times180°, z),$ где $n$ — любое целое число. Более того, если радиус $ρ$ равен нулю, азимут произволен.

В ситуациях, когда кому-то нужен уникальный набор координат для каждой точки, можно ограничить радиус неотрицательным ( ρ $\geq 0$ ), а азимут $φ$ лежать в определенном интервале, охватывающем 360 °, например $[-180 °, +180°]$ или $[0,360°]$ .

Конвенции

Обозначения цилиндрических координат неоднородны. Стандарт ISO — 31-11 рекомендует $(ρ, φ, z)$ , где $ρ$ — радиальная координата, $φ$ азимут, а $z$ — высота. Однако радиус также часто обозначается $r$ или $s$ , азимут — $θ$ или $t$ , а третья координата — $h$ или (если цилиндрическая ось считается горизонтальной) $x$ или любой буквой, зависящей от контекста.

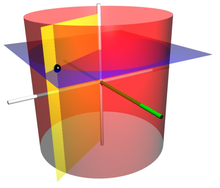
В конкретных ситуациях и во многих математических иллюстрациях положительная угловая координата измеряется против часовой стрелки, если смотреть из любой точки с положительной высотой.

Преобразования системы координат

Цилиндрическая система координат — одна из многих трехмерных систем координат. Для преобразования между ними можно использовать следующие формулы.

Декартовы координаты

Для преобразования цилиндрических и декартовых координат удобно предположить, что опорной плоскостью первой является декартова $плоскость xy$ (с уравнением $z = 0$ ), а цилиндрической осью является декартова $ось z$ . Тогда $координата z$ одинакова в обеих системах, а соответствие между цилиндрическими $(ρ, φ, z)$ и декартовыми $(x, y, z)$ такое же, как и для полярных координат, а именно ${\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}$ в одном направлении и ${\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &={\begin{cases}{\text{indeterminate}}&{\text{if }}x=0{\text{ and }}y=0\\\arcsin \left({\frac {y}{\rho }}\right)&{\text{if }}x\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y<0\end{cases}}\end{aligned}}$ в другом. Функция арксинус является обратной функцией синуса и, как предполагается, возвращает угол в диапазоне $[- .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ π / 2 ⁠ , + ⁠ π / 2 ⁠ ]$ = $[-90°, +90°]$ . Эти формулы дают азимут $φ$ в диапазоне $[-90°, +270°]$ .

Используя функцию арктангенса , которая также возвращает угол в диапазоне $[- ⁠ π / 2 ⁠, + ⁠ π / 2 ⁠]$ = $[-90°, +90°]$ , можно также вычислить $\varphi$ без вычислений $\rho$ первый ${\begin{aligned}\varphi &={\begin{cases}{\text{indeterminate}}&{\text{if }}x=0{\text{ and }}y=0\\{\frac {\pi }{2}}{\frac {y}{|y|}}&{\text{if }}x=0{\text{ and }}y\neq 0\\\arctan \left({\frac {y}{x}}\right)&{\mbox{if }}x>0\\\arctan \left({\frac {y}{x}}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y\geq 0\\\arctan \left({\frac {y}{x}}\right)-\pi &{\mbox{if }}x<0{\text{ and }}y<0\end{cases}}\end{aligned}}$ Остальные формулы смотрите в статье Полярная система координат .

Многие современные языки программирования предоставляют функцию, которая вычисляет правильный азимут $φ$ в диапазоне $(-π, π)$ по заданным x и y без необходимости выполнять анализ случая, как указано выше. Например, эту функцию вызывает atan2 ( y , x ) на языке программирования C и (atan y x ) в Common Lisp .

Сферические координаты

Сферические координаты (радиус $r$ , высота или наклон $θ$ , азимут $φ$ ) могут быть преобразованы в цилиндрические координаты или из них, в зависимости от того, представляет ли $θ$ высоту или наклон, следующим образом:

Преобразование между сферическими и цилиндрическими координатами
Преобразование в:	Координировать	$θ$ - высота	$θ$ - наклон
Цилиндрический	$ρ$ =	$р потому что θ$	$р грех я$
	$φ$ =	$ж$
	$г$ =	$р грех я$	$р потому что θ$
сферический	$р$ =	${\textstyle {\sqrt {\rho ^{2}+z^{2}}}}$
	$θ$ =	${\textstyle \arctan \left({\frac {z}{\rho }}\right)}$	${\textstyle \arctan \left({\frac {\rho }{z}}\right)}$
	$φ$ =	$ж$

Элементы линии и объема

Во многих задачах, связанных с цилиндрическими полярными координатами, полезно знать элементы линии и объема; они используются при интеграции для решения проблем, связанных с путями и объемами.

Линейный элемент $\mathrm {d} {\boldsymbol {r}}=\mathrm {d} \rho \,{\boldsymbol {\hat {\rho }}}+\rho \,\mathrm {d} \varphi \,{\boldsymbol {\hat {\varphi }}}+\mathrm {d} z\,{\boldsymbol {\hat {z}}}.$

Элемент объема $\mathrm {d} V=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi \,\mathrm {d} z.$

Элемент поверхности на поверхности постоянного радиуса $ρ$ (вертикальный цилиндр) равен $\mathrm {d} S_{\rho }=\rho \,\mathrm {d} \varphi \,\mathrm {d} z.$

Элемент поверхности на поверхности постоянного азимута $φ$ (вертикальная полуплоскость) равен $\mathrm {d} S_{\varphi }=\mathrm {d} \rho \,\mathrm {d} z.$

Элемент поверхности на поверхности постоянной высоты $z$ (горизонтальная плоскость) равен $\mathrm {d} S_{z}=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi .$

Оператор del в этой системе приводит к следующим выражениям для градиента , дивергенции , ротора и лапласиана : ${\begin{aligned}\nabla f&={\frac {\partial f}{\partial \rho }}{\boldsymbol {\hat {\rho }}}+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}{\boldsymbol {\hat {\varphi }}}+{\frac {\partial f}{\partial z}}{\boldsymbol {\hat {z}}}\\[8px]\nabla \cdot {\boldsymbol {A}}&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho A_{\rho }\right)+{\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}\\[8px]\nabla \times {\boldsymbol {A}}&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\boldsymbol {\hat {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\boldsymbol {\hat {\varphi }}}+{\frac {1}{\rho }}\left({\frac {\partial }{\partial \rho }}\left(\rho A_{\varphi }\right)-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\boldsymbol {\hat {z}}}\\[8px]\nabla ^{2}f&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial f}{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}\end{aligned}}$

Цилиндрические гармоники

Решения уравнения Лапласа в системе цилиндрической симметрии называются цилиндрическими гармониками .

Кинематика

В цилиндрической системе координат положение частицы можно записать как ^[6] ${\boldsymbol {r}}=\rho \,{\boldsymbol {\hat {\rho }}}+z\,{\boldsymbol {\hat {z}}}.$ Скорость частицы есть производная по времени от ее положения: ${\boldsymbol {v}}={\frac {\mathrm {d} {\boldsymbol {r}}}{\mathrm {d} t}}={\dot {\rho }}\,{\boldsymbol {\hat {\rho }}}+\rho \,{\dot {\varphi }}\,{\hat {\boldsymbol {\varphi }}}+{\dot {z}}\,{\hat {\boldsymbol {z}}},$ где термин $\rho {\dot {\varphi }}{\hat {\varphi }}$ получается из формулы Пуассона ${\frac {\mathrm {d} {\hat {\rho }}}{\mathrm {d} t}}={\dot {\varphi }}{\hat {z}}\times {\hat {\rho }}$ . Его ускорение равно ^[6] ${\boldsymbol {a}}={\frac {\mathrm {d} {\boldsymbol {v}}}{\mathrm {d} t}}=\left({\ddot {\rho }}-\rho \,{\dot {\varphi }}^{2}\right){\boldsymbol {\hat {\rho }}}+\left(2{\dot {\rho }}\,{\dot {\varphi }}+\rho \,{\ddot {\varphi }}\right){\hat {\boldsymbol {\varphi }}}+{\ddot {z}}\,{\hat {\boldsymbol {z}}}$

См. также

Ссылки

^ Крафт, К.; Волокитин А.С. (1 января 2002 г.). «Резонансное взаимодействие электронного пучка с несколькими низшими гибридными волнами» . Физика плазмы . 9 (6): 2786–2797. Бибкод : 2002PhPl....9.2786K . дои : 10.1063/1.1465420 . ISSN 1089-7674 . Архивировано из оригинала 14 апреля 2013 года . Проверено 9 февраля 2013 г. ...в цилиндрических координатах $(r, θ, z)$ ... и $Z = v bz t$ — продольное положение...
^ Гройсман, Александр; Стейнберг, Виктор (1997). «Пары одиночных вихрей в вязкоупругом течении Куэтта». Письма о физических отзывах . 78 (8): 1460–1463. arXiv : patt-sol/9610008 . Бибкод : 1997PhRvL..78.1460G . дои : 10.1103/PhysRevLett.78.1460 . S2CID 54814721 . ...где $r$ , $θ$ и $z$ — цилиндрические координаты... как функция осевого положения...
^ Шимански, Дж. Э. (1989). Базовая математика для инженеров-электронщиков: модели и приложения . Учебные пособия по электронной технике (№ 16). Тейлор и Фрэнсис. п. 170. ИСБН 978-0-278-00068-1 .
^ Нанн, Роберт Х. (1989). Промежуточная механика жидкости . Тейлор и Фрэнсис. п. 3. ISBN 978-0-89116-647-4 .
^ Спарк, Линда Шивон ; Галлахер, Джон Силл (2007). Галактики во Вселенной: Введение (2-е изд.). Издательство Кембриджского университета. п. 37. ИСБН 978-0-521-85593-8 .
↑ Перейти обратно: Перейти обратно: ^а ^б Тейлор, Джон Р. (2005). Классическая механика . Саусалито, Калифорния: Университетские научные книги. п. 29.

Дальнейшее чтение

Морс, Филип М .; Фешбах, Герман (1953). Методы теоретической физики . Часть I. Нью-Йорк : МакГроу-Хилл . стр. 656–657. ISBN 0-07-043316-Х . LCCN 52011515 .
Маргенау, Генри ; Мерфи, Джордж М. (1956). Математика физики и химии . Нью-Йорк: Д. ван Ностранд. п. 178 . ISBN 9780882754239 . LCCN 55010911 . ОСЛК 3017486 .
Корн, Гранино А.; Корн, Тереза М. (1961). Математический справочник для ученых и инженеров . Нью-Йорк: МакГроу-Хилл. стр. 174–175 . LCCN 59014456 . АСИН B0000CKZX7.
Зауэр, Роберт; Сабо, Иштван (1967). Математический инструментарий инженера . Нью-Йорк: Springer Verlag . п. 95. LCCN 67025285 .
Цвиллингер, Дэниел (1992). Справочник по интеграции . Бостон : Издательство Джонс и Бартлетт . п. 113. ИСБН 0-86720-293-9 . ОСЛК 25710023 .
Мун, П.; Спенсер, Делавэр (1988). «Координаты кругового цилиндра (r, ψ, z)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд.). Нью-Йорк: Springer-Verlag. стр. 12–17, табл. 1.02. ISBN 978-0-387-18430-2 .

Внешние ссылки

«Цилиндрические координаты» , Математическая энциклопедия , EMS Press , 2001 [1994]
Описание цилиндрических координат в MathWorld
Цилиндрические координаты. Анимация, иллюстрирующая цилиндрические координаты Фрэнка Ваттенберга.

[1] Крафт, К.; Волокитин А.С. (1 января 2002 г.). «Резонансное взаимодействие электронного пучка с несколькими низшими гибридными волнами» . Физика плазмы . 9 (6): 2786–2797. Бибкод : 2002PhPl....9.2786K . дои : 10.1063/1.1465420 . ISSN 1089-7674 . Архивировано из оригинала 14 апреля 2013 года . Проверено 9 февраля 2013 г. ...в цилиндрических координатах $(r, θ, z)$ ... и $Z = v bz t$ — продольное положение...

[2] Гройсман, Александр; Стейнберг, Виктор (1997). «Пары одиночных вихрей в вязкоупругом течении Куэтта». Письма о физических отзывах . 78 (8): 1460–1463. arXiv : patt-sol/9610008 . Бибкод : 1997PhRvL..78.1460G . дои : 10.1103/PhysRevLett.78.1460 . S2CID 54814721 . ...где $r$ , $θ$ и $z$ — цилиндрические координаты... как функция осевого положения...

[3] Шимански, Дж. Э. (1989). Базовая математика для инженеров-электронщиков: модели и приложения . Учебные пособия по электронной технике (№ 16). Тейлор и Фрэнсис. п. 170. ИСБН 978-0-278-00068-1 .

[4] Нанн, Роберт Х. (1989). Промежуточная механика жидкости . Тейлор и Фрэнсис. п. 3. ISBN 978-0-89116-647-4 .

[5] Спарк, Линда Шивон ; Галлахер, Джон Силл (2007). Галактики во Вселенной: Введение (2-е изд.). Издательство Кембриджского университета. п. 37. ИСБН 978-0-521-85593-8 .

[Taylor-6] Перейти обратно: Перейти обратно: ^а ^б Тейлор, Джон Р. (2005). Классическая механика . Саусалито, Калифорния: Университетские научные книги. п. 29.

[1]

[2]

[3]

[4]

[5]

[6]