Кривая Лиссажу

Кривая Лиссажу / ˈ l ɪ s ə ʒ uː / , также известная как фигура Лиссажу или кривая Боудича / ˈ b aʊ d ɪ tʃ / , представляет собой график системы параметрических уравнений.

x=A\sin(at+\delta ),\quad y=B\sin(bt),

которые описывают суперпозицию двух перпендикулярных колебаний в направлениях x и y с разной угловой частотой ( a и b). Полученное семейство кривых было исследовано Натаниэлем Боудичем в 1815 году, а затем более подробно в 1857 году Жюлем Антуаном Лиссажу (в честь которого оно было названо). Такие движения можно рассматривать как особый вид сложного гармонического движения .

Внешний вид фигуры чувствителен к соотношению $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ а / б ⁠$ . Для отношения 1, когда частоты соответствуют a=b, фигура представляет собой эллипс , в особых случаях включая круги ( $A = B$ , $δ = ⁠ π / 2 ⁠$ радиан ) и линии ( $δ знак равно 0$ ). Небольшое изменение одной из частот будет означать, что колебание x после одного цикла будет немного не синхронизировано с движением y, и поэтому эллипс не сможет замкнуться и проследить кривую, слегка примыкающую к ней на следующем витке, что будет проявляться как прецессия эллипс. Паттерн закрывается, если частоты представляют собой целочисленные отношения, т.е. $⁠ a / b ⁠$ рационально .

Еще одна простая фигура Лиссажу — парабола ( $⁠ б / а ⁠ знак равно 2$ , $δ знак равно ⁠ π / 4 ⁠$ ). Опять же, небольшой сдвиг на одну частоту от отношения 2 приведет к тому, что трасса не закроется, а выполнит несколько циклов, последовательно сдвигаемых только закрытие, если соотношение будет рациональным, как и раньше. Может образоваться сложный плотный узор (см. ниже).

Визуальная форма таких кривых часто напоминает трехмерный узел , и действительно, многие виды узлов, в том числе известные как узлы Лиссажу , проецируются на плоскость как фигуры Лиссажу.

Визуально соотношение $⁠a b⁠ / количество «лепестков » определяет$ фигуры. Например, соотношение ⁠ 3 / 1 ⁠ или ⁠ 1 / 3 ⁠ дает фигуру с тремя основными лепестками (см. изображение). Аналогично, соотношение ⁠ 5 / 4 ⁠ создает фигуру с пятью горизонтальными лепестками и четырьмя вертикальными лепестками. Рациональные соотношения создают замкнутые (связные) или «неподвижные» фигуры, тогда как иррациональные соотношения создают фигуры, которые кажутся вращающимися. Соотношение $⁠ A / B ⁠$ определяет относительное соотношение ширины и высоты кривой. Например, соотношение ⁠ 2/1 фигуру , ⁠ дает ширина которой в два раза превышает высоту. Наконец, значение $δ$ определяет видимый угол «поворота» фигуры, рассматриваемой так, как если бы она на самом деле была трехмерной кривой. Например, $δ = 0$ при $компоненты x$ и $y$ находятся точно в фазе, поэтому результирующая фигура выглядит как кажущаяся трехмерная фигура, если смотреть прямо (0°). Напротив, любое ненулевое $δ$ создает фигуру, которая кажется повернутой либо влево-вправо, либо вращение вверх-вниз (в зависимости от соотношения $⁠ a / b ⁠$ ).

Окружность – это простая кривая Лиссажу.

Фигуры Лиссажу, где $a = 1$ , $b = N$ ( $N$ — натуральное число ) и

\delta ={\frac {N-1}{N}}{\frac {\pi }{2}}

являются полиномами Чебышева первого рода степени $N$ . Это свойство используется для создания набора точек, называемых точками Падуи , в которых функция может быть выбрана для вычисления либо двумерной интерполяции, либо квадратуры функции в области $[-1,1] \times [-1,1 ]$ .

Связь некоторых кривых Лиссажу с полиномами Чебышева становится более понятной, если кривая Лиссажу, порождающая каждую из них, выражается с использованием косинус-функций, а не синусоидальных функций.

x=\cos(t),\quad y=\cos(Nt)

Примеры

Анимация, показывающая адаптацию кривой как соотношение $⁠ a / b ⁠$ увеличивается от 0 до 1

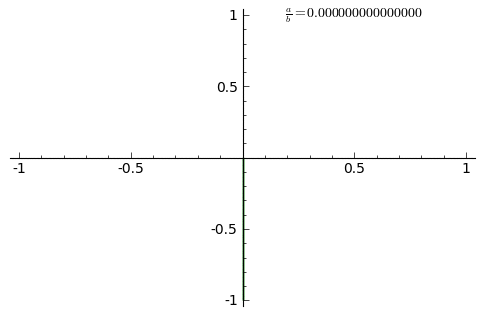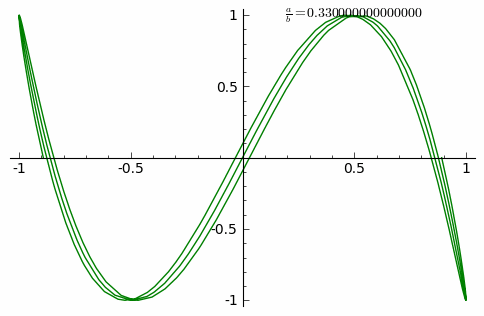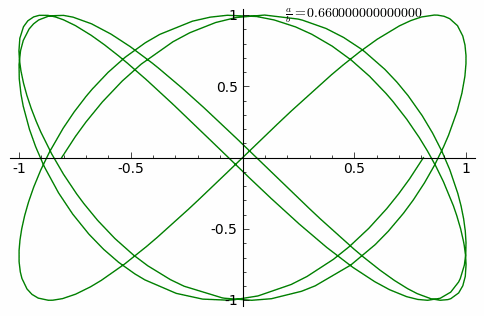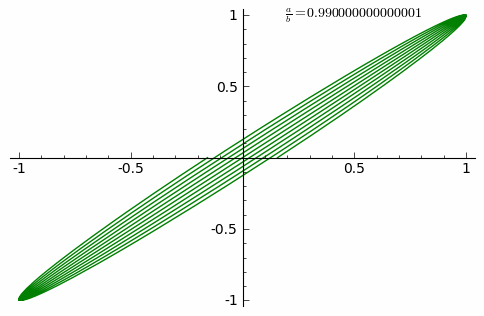
Анимация показывает адаптацию кривой с постоянно увеличивающимся $⁠ a / b ⁠$ дробь от 0 до 1 с шагом 0,01 ( $δ = 0$ ).

Ниже приведены примеры фигур Лиссажу с нечетным натуральным числом $a$ , четным натуральным числом $b$ и $| а - б | = 1$ .

$д = ⁠ π / 2 ⁠$ , $а знак равно 1$ , $б знак равно 2$ (1:2)
$д = ⁠ π / 2 ⁠$ , $а = 3$ , $б = 2$ (3:2)
$д = ⁠ π / 2 ⁠$ , $а = 3$ , $б = 4$ (3:4)
$д = ⁠ π / 2 ⁠$ , $а знак равно 5$ , $б знак равно 4$ (5:4)
Фигуры Лиссажу: различные частотные соотношения и разности фаз

Поколение

До появления современного электронного оборудования кривые Лиссажу можно было генерировать механически с помощью гармониграфа .

Практическое применение

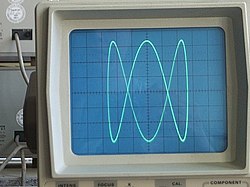
Кривые Лиссажу также можно построить с помощью осциллографа (как показано на рисунке). Схема осьминога может использоваться для демонстрации изображений сигналов на осциллографе. Два сдвинутых по фазе синусоидальных входа подаются на осциллограф в режиме XY, а фазовое соотношение между сигналами представляется в виде фигуры Лиссажу.

В мире профессионального аудио этот метод используется для анализа фазового соотношения между левым и правым каналами стереоаудиосигнала в реальном времени. В более крупных и сложных микшерных консолях для этой цели может быть встроен осциллограф.

На осциллографе мы предполагаем, что $x$ — это CH1, а $y$ — это CH2, $A$ — это амплитуда CH1, а $B$ — это амплитуда CH2, $a$ — это частота CH1, а $b$ — это частота CH2, поэтому $⁠ a / b ⁠$ — соотношение частот двух каналов, а $δ$ — фазовый сдвиг СН1.

Чисто механическое применение кривой Лиссажу с $a = 1$ , $b = 2$ находится в приводном механизме ламп с качающимся лучом типа Mars Light, популярных на железных дорогах в середине 1900-х годов. В некоторых версиях балка имеет на своей стороне однобокий узор в виде восьмерки.

Приложение для случая $a = b$

На этом рисунке обе входные частоты идентичны, но разность фаз между ними создает форму эллипса .

Когда входной сигнал системы LTI имеет синусоидальную форму, выходной сигнал является синусоидальным с той же частотой, но может иметь другую амплитуду и некоторый сдвиг фазы . Использование осциллографа , который может отображать один сигнал в зависимости от другого (в отличие от одного сигнала в зависимости от времени), для построения графика выходного сигнала системы LTI в зависимости от входного сигнала системы LTI, дает эллипс, который представляет собой фигуру Лиссажу для особого случая $a = b.$ . Соотношение сторон полученного эллипса является функцией фазового сдвига между входом и выходом, при этом соотношение сторон 1 (идеальный круг) соответствует фазовому сдвигу ±90 °, а соотношение сторон ∞ (линия) соответствует до фазового сдвига 0° или 180°. ^{[ нужна ссылка ]}

На рисунке ниже показано, как изменяется фигура Лиссажу при различных фазовых сдвигах. Все фазовые сдвиги отрицательны, поэтому задержки семантику можно использовать с причинно-следственной системой LTI (обратите внимание, что -270° эквивалентно +90°). Стрелки показывают направление вращения фигуры Лиссажу. ^{[ нужна ссылка ]}

В инженерном деле

Кривая Лиссажу используется в экспериментальных тестах, чтобы определить, можно ли правильно отнести устройство к мемристору . ^{[ нужна ссылка ]} Он также используется для сравнения двух разных электрических сигналов: известного опорного сигнала и тестируемого сигнала. ^[1]^[2]

В популярной культуре

В кинофильмах

Лиссажу анимация

Фигуры Лиссажу иногда отображались на осциллографах, предназначенных для имитации высокотехнологичного оборудования в научно-фантастических телешоу и фильмах 1960-х и 1970-х годов. ^[3]

Заголовок основан Джона Уитни к художественному фильму Альфреда Хичкока 1958 года «Головокружение» на фигурах Лиссажу. ^[4]

Логотипы компании

Фигуры Лиссажу иногда используются в графическом дизайне в качестве логотипов . Примеры включают в себя:

Австралийская радиовещательная корпорация ( $a = 1$ , $b = 3$ , $δ = ⁠ π / 2 ⁠$ ) ^[5]
Лаборатория Линкольна в Массачусетском технологическом институте ( $a = 3$ , $b = 4$ , $δ = ⁠ π / 2 ⁠$ ) ^[6]
Клуб под открытым небом Else в Берлине ( $a = 3$ , $b = 2$ , $δ = ⁠ π / 2 ⁠$ )
Университет электрокоммуникаций , Япония ( $a = 5$ , $b = 6$ , $δ = ⁠ π / 2 ⁠$ ). ^{[ нужна ссылка ]}
Приложение потокового видео Disney's Movies Anywhere использует стилизованную версию кривой.
Meta Ребрендинг Facebook в Platforms также представляет собой кривую Лиссажу, повторяющую форму заглавной буквы M ( $a = 1$ , $b = -2$ , $δ = ⁠ π / 20 ⁠$ ).
Домашняя государственная пивоваренная компания. Используется в качестве их логотипа и обозначает как отдельный момент, так и течение времени - Ichi-go ichi-e.

По-современному

Макс -дадаист Художник Эрнст рисовал фигуры Лиссажу непосредственно, водя проколотым ведром с краской по холсту. ^[7]

В музыкальном образовании

Кривые Лиссажу использовались в прошлом для графического представления музыкальных интервалов с помощью Гармонографа . ^[8] устройство, состоящее из маятников, колеблющихся с разным соотношением частот. Поскольку разные системы настройки используют разные соотношения частот для определения интервалов, их можно сравнить с помощью кривых Лиссажу, чтобы увидеть их различия. ^[9] Таким образом, кривые Лиссажу находят применение в музыкальном образовании, поскольку графически представляют различия между интервалами и системами настройки.

См. также

Примечания

^ Палмер, Кеннет; Риджуэй, Тим; Аль-Рави, Омар; и др. (сентябрь 2011 г.). «Цифры Лиссажу: инженерный инструмент для анализа первопричин отдельных случаев — предварительная концепция» . Журнал экстракорпоральных технологий . 43 (3): 153–156. ISSN 0022-1058 . ПМЦ 4679975 . ПМИД 22164454 .
^ «Кривые Лиссажу» . datagenetics.com . Проверено 10 июля 2020 г.
^ «Долгий путь до фигур Лиссажу» . Новый учёный . Деловая информация Рида: 77. 24 сентября 1987 г. ISSN 0262-4079 .
^ МакКормак, Том (9 мая 2013 г.). «Внедрил ли «Головокружение» компьютерную графику в кино?» . сайт rhizome.org . Проверено 18 декабря 2020 г.
^ «Азбука фигур Лиссажу» . abc.net.au. Австралийская радиовещательная корпорация.
^ «Логотип лаборатории Линкольна» . ll.mit.edu . Лаборатория Линкольна , Массачусетский технологический институт . 2008 год . Проверено 12 апреля 2008 г.
^ Кинг, М. (2002). «От Макса Эрнста до Эрнста Маха: эпистемология в искусстве и науке» (PDF) . Проверено 17 сентября 2015 г.
^ Уитти, Х. Ирвин (1893). Гармонограф . Норидж, Ярмут и Лондон: принтеры Jarrold & Sons.
^ Сьерра, Калифорния (2023 г.). «Повторяемость кривых Лиссажу и визуальное представление систем настройки» . Основы науки . дои : 10.1007/s10699-023-09930-z .

Внешние ссылки

Кривая Лиссажу в Mathworld

Интерактивные демонстрации

3D-апплеты Java, изображающие построение кривых Лиссажу в осциллографе:
- Учебник от НХМФЛ
- Апплет по физике от Chiu-king Ng
Подробное моделирование фигур Лиссажу Рисование фигур Лиссажу с помощью интерактивных ползунков на Javascript
Кривые Лиссажу: интерактивное моделирование графических представлений музыкальных интервалов и вибрирующих струн.
Интерактивный генератор кривых Лиссажу — апплет Javascript с использованием JSXGraph
Анимированные фигурки Лиссажу
[1] Wolfram Mathematica — фигуры Лиссажу с интерактивными ползунками в Wolfram Mathematica.

[1] Палмер, Кеннет; Риджуэй, Тим; Аль-Рави, Омар; и др. (сентябрь 2011 г.). «Цифры Лиссажу: инженерный инструмент для анализа первопричин отдельных случаев — предварительная концепция» . Журнал экстракорпоральных технологий . 43 (3): 153–156. ISSN 0022-1058 . ПМЦ 4679975 . ПМИД 22164454 .

[2] «Кривые Лиссажу» . datagenetics.com . Проверено 10 июля 2020 г.

[Information1987-3] «Долгий путь до фигур Лиссажу» . Новый учёный . Деловая информация Рида: 77. 24 сентября 1987 г. ISSN 0262-4079 .

[4] МакКормак, Том (9 мая 2013 г.). «Внедрил ли «Головокружение» компьютерную графику в кино?» . сайт rhizome.org . Проверено 18 декабря 2020 г.

[5] «Азбука фигур Лиссажу» . abc.net.au. Австралийская радиовещательная корпорация.

[6] «Логотип лаборатории Линкольна» . ll.mit.edu . Лаборатория Линкольна , Массачусетский технологический институт . 2008 год . Проверено 12 апреля 2008 г.

[7] Кинг, М. (2002). «От Макса Эрнста до Эрнста Маха: эпистемология в искусстве и науке» (PDF) . Проверено 17 сентября 2015 г.

[8] Уитти, Х. Ирвин (1893). Гармонограф . Норидж, Ярмут и Лондон: принтеры Jarrold & Sons.

[9] Сьерра, Калифорния (2023 г.). «Повторяемость кривых Лиссажу и визуальное представление систем настройки» . Основы науки . дои : 10.1007/s10699-023-09930-z .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]