Твердая геометрия

Твердотельная геометрия или стереометрия — это геометрия трехмерного (3D - евклидова пространства пространства). ^[1]

Сплошная фигура — это область трехмерного пространства, ограниченная двумерной поверхностью ; например, твердый шар состоит из сферы и ее внутренней части .

Геометрия твердого тела занимается измерением объемов пирамиды различных твердых тел, включая , призмы ( и другие многогранники ), кубы , цилиндры , конусы (и усеченные конусы ). ^[2]

История

Пифагорейцы имели дело с правильными твердыми телами , но пирамида, призма, конус и цилиндр не были изучены до платоников . Евдокс установил их размеры, доказав, что пирамида и конус имеют одну треть объема призмы и цилиндра на том же основании и одинаковой высоты. Вероятно, он также был первооткрывателем доказательства того, что объем, заключенный в сфере, пропорционален кубу ее радиуса . ^[3]

Темы

Основные темы твердотельной геометрии и стереометрии включают:

падение плоскостей и прямых
двугранный угол и телесный угол
куб , кубоид , параллелепипед
тетраэдр другие и пирамиды
призмы
октаэдр , додекаэдр , икосаэдр
конусы и цилиндры
сфера
другие квадрики : сфероид , эллипсоид , параболоид и гиперболоид .

Расширенные темы включают в себя:

проективная геометрия трех измерений (приводящая к доказательству теоремы Дезарга с использованием дополнительного измерения)
дальнейшие многогранники
начертательная геометрия .

Список твердых цифр

В то время как сфера — это поверхность шара , для других твердых фигур иногда неясно, относится ли этот термин к поверхности фигуры или к объему, заключенному в ней, особенно для цилиндра .

Основные типы фигур, которые либо составляют, либо определяют объем.
Фигура	Определения	Изображения
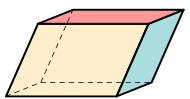Параллелепипед	Многогранник ), каждая из с шестью гранями ( шестигранник которых является параллелограммом. Шестигранник с тремя парами параллельных граней. Призма , основанием которой является параллелограмм.
Ромбоэдр	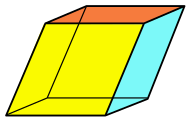Параллелепипед , у которого все ребра одинаковой длины. Куб ромбы , только грани у него не квадраты, а .
Кубовидный	Выпуклый многогранник, ограниченный шестью четырехугольными гранями, граф многогранника которого такой же, как у куба. ^[4] Некоторые источники также требуют, чтобы каждая из граней была прямоугольником ( чтобы каждая пара соседних граней встречалась под прямым углом ). Этот более строгий тип кубоида также известен как прямоугольный кубоид , правильный кубоид , прямоугольный ящик , прямоугольный шестигранник , прямая прямоугольная призма или прямоугольный параллелепипед . ^[5]
Многогранник	Плоские многоугольные грани , прямые края и острые углы или вершины.	Малый звездчатый додекаэдр Тороидальный многогранник
Однородный многогранник	Правильные многоугольники являются гранями и являются вершинно-транзитивными (т. е. существует изометрия, отображающая любую вершину на любую другую).	Тетраэдр Курносый додекаэдр
Призма	Многогранник , состоящий из n- стороннего многоугольного основания , второго основания, являющегося транслированной копией (жестко перемещаемой без вращения) первого, и n других граней (обязательно всех параллелограммов ), соединяющих соответствующие стороны двух оснований.
Конус	Плавно сужается от плоского основания (часто, хотя и не обязательно, круглого) к точке, называемой вершиной или вершиной.	Прямой круговой конус и наклонный круговой конус.
Цилиндр	Прямые параллельные стороны и круглое или овальное поперечное сечение.	Сплошной эллиптический цилиндр Прямой и косой круговые цилиндры
Эллипсоид	Поверхность, которую можно получить из сферы путем ее деформации посредством направленного масштабирования или, в более общем смысле, аффинного преобразования.	Примеры эллипсоидов с уравнением ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:$ сфера (вверху, a=b=c=4), сфероид (слева внизу, a=b=5, c=3), трехосный эллипсоид (внизу справа, a=4,5, b=6, c=3)
Лимон	Линза (или менее половины дуги окружности) вращается вокруг оси , проходящей через конечные точки линзы (или дуги). ^[6]
Гиперболоид	Поверхность , созданная вращением гиперболы вокруг одной из ее главных осей.

Техники

В твердотельной геометрии используются различные методы и инструменты. Среди них большое влияние оказывают аналитическая геометрия и векторные методы, позволяющие систематически использовать линейные уравнения и матричную алгебру, которые важны для более высоких измерений.

Приложения

Основное применение твердотельной геометрии и стереометрии находится в компьютерной 3D-графике .

См. также

Примечания

^ Британское руководство по геометрии , Britannica Educational Publishing, 2010, стр. 67–68.
^ Kiselev 2008 .
↑ Перефразировано и частично взято из Британской энциклопедии 1911 года .
^ Робертсон, Стюарт Александр (1984). Многогранники и симметрия . Издательство Кембриджского университета. п. 75 . ISBN 9780521277396 .
^ Дюпюи, Натан Феллоуз (1893). Элементы синтетической твердотельной геометрии . Макмиллан. п. 53 . Проверено 1 декабря 2018 г.
^ Вайсштейн, Эрик В. «Лимон» . Вольфрам Математический мир . Проверено 4 ноября 2019 г.

Ссылки

Киселев, АП (2008). Геометрия . Том. Книга II. Стереометрия. Перевод Гивенталя, Александра. Сумиздат.

[1] Британское руководство по геометрии , Britannica Educational Publishing, 2010, стр. 67–68.

[2] Kiselev 2008 .

[3] Перефразировано и частично взято из Британской энциклопедии 1911 года .

[4] Робертсон, Стюарт Александр (1984). Многогранники и симметрия . Издательство Кембриджского университета. п. 75 . ISBN 9780521277396 .

[5] Дюпюи, Натан Феллоуз (1893). Элементы синтетической твердотельной геометрии . Макмиллан. п. 53 . Проверено 1 декабря 2018 г.

[mathworld-6] Вайсштейн, Эрик В. «Лимон» . Вольфрам Математический мир . Проверено 4 ноября 2019 г.

[1]

[2]

[3]

[4]

[5]

[6]